Coupler Design Issues from the Modular Ocean Data

Coupler Design Issues from the Modular Ocean Data Assimilation Project Dr. Richard Loft Computational Science Section Scientific Computing Division National Center for Atmospheric Research Boulder, CO USA

Outline Project Introduction – goals / pariticipants/ scope – http//: iom. asu. edu IOM: weak variationaldata assimilation – Inputs/outputs – Data components – Functional components IOM Coupling design – Strategy – Details – Role of Domain Specific Languages (DSL)

Modular Ocean Data Assimilation NSF ITR/AP Focus on the OSUInverse Ocean Model (IOM) system for ocean data assimilation. – Variationaldata assimilation system – Weak assimilation – Iterativealgorithm for solving nonlinear assimilation problems – Suite of diagnostics (posterior error statistics) – 20 years in development by Bennett, et al.

Objectives of MODA Project Enhance the IOM System with modern information technology. – – Modular software design Hybrid parallel implementation Coupled model strategy Automated code generation Distributeit to the ocean modeling community. – 5 ocean modeling partners Facilitateapplication of the system to coastal oceans, ocean basins and the global ocean.

NSF ITR MODA Collaboration Institution Arizona State U. U. Colorado NCAR NCSA U. North Carolina Oregon State U Erwig Rutgers U. UCSD ( Scripps) Researcher Muccino Moore Loft Baker Leuttich Bennett, Egbert, Arango, Haidvogel Cornuelle, Miller

IOM Team Members IOM-PEZ Parallelism – PI: Rich Loft, NCAR – Component: parallel super and Infra-structure (hybrid F 90 module framework) Domain Specific Languages – PIs: Martin Erwig & Zhu Fu, OSU – Component: automated code generator (Haskell) Visualization – Pis: Polly Baker, NCSA/IU – Component: Vis. Bench. Tool. Visualization Software

Participating Model Teams PEZ (Primitive Eq. Z-coordinate) model – Description: 3 D, free-surface, z-coordinate • Bryan-Cox – Grid: spherical polar, “B” grid – Language: F 90 – Parallelism: SPMD, MPI ROMS (Regional Ocean Model System) – Description: 3 D, free-surface, S-coordinate – Grid: Horizontal orthogonal curvilinear coordinate, “C” grid – Language: F 90 – Parallelism: SPMD, Open. MP MPI, SMS ,

Participating Model Teams SEOM (Spectral Element Ocean Model) – – – PI: Dale Haidvogel Rutgers , Description: 3 D, free-surface, S-coordinate Grid: h-p finite element, quadrilateral element Language: F 90 Parallelism: SPMD, MPI ADCIRC (Advanced Circulation) model – PIs: Julia Muccino ASU; Rich Luettich UNC , , – Description: 3 D, free-surface, sigma-coordinate – Grid: finite element, linear triangular element Language: F 90 – Parallelism: SPMD, MPI

Participating Model Teams OTIS (Internal Tides) – PI: Gary Egbert OSU , – Description: Laplace tidal equations plus 10 years of TOPEX/Poseidon – Description: Solid Earthmageto-tellurics (magnetic field of earth’s crust)

Data Assimilation Checklist: Inputs observing system – e. g. measured sea surface temperatures, isotherm depths and surface winds dynamics – e. g. the hydrostatic primitive equations hypothesis concerning the error – covariancesof errors in the • initial conditions • boundary conditions • and forcing estimator – space-time integrated weighted sum of squared errors optimization algorithm – iterative indirect representeralgorithm

Data Assimilation Checklist: Outputs state estimate – hindcast over the period in the data collection – space-time fields for state variables data residuals, dynamic residuals – Space-time minimum residuals posterior error statistics – space-time covariances test statistics – chi square internal consistency tests model improvements – e. g. suggested from the distribution of errors observing system assessment

Inverse system data components… Vector of data to be assimilated Trajectories – multi-variate physical space-time fields – generated by tangent linear/ adjoint model – user prescribed Parameters – covariance matrices – user prescribed

Inverse system functional components… Pure data space components – iterative solver Physical space components – tangent linear/adjoint models Components that map between the two spaces. – measurement operator – impulse operator Looks like a coupled system

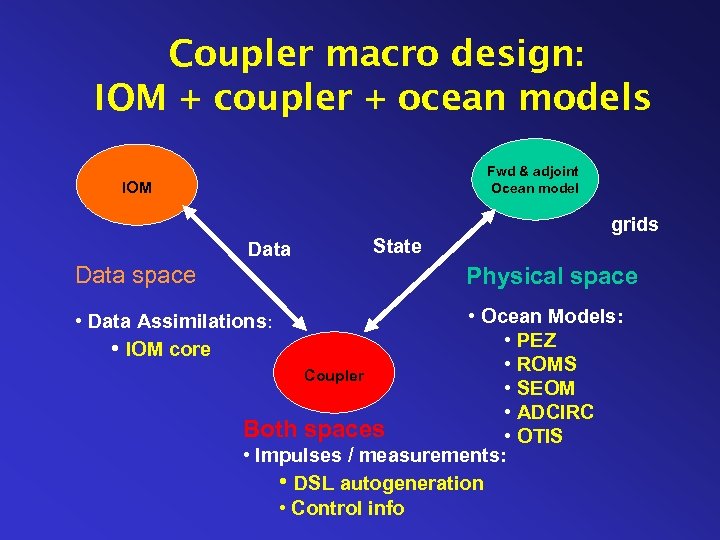Coupler macro design: IOM + coupler + ocean models Fwd & adjoint Ocean model IOM grids Data space State Physical space • Ocean Models: • PEZ • ROMS Coupler • SEOM • ADCIRC Both spaces • OTIS • Impulses / measurements: • DSL autogeneration • Control info • Data Assimilations: • IOM core

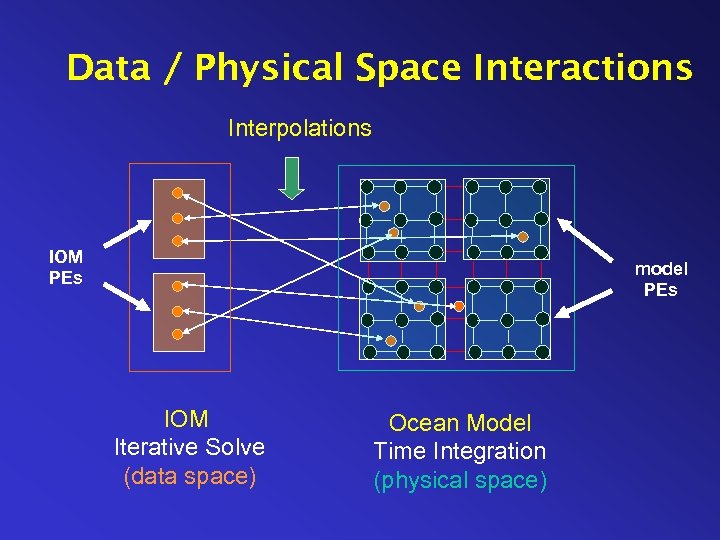Data / Physical Space Interactions Interpolations IOM PEs model PEs IOM Iterative Solve (data space) Ocean Model Time Integration (physical space)

IOM System Pseudo-code IOM(){ read d first( ; u. F) h = d - u. F ^ solve(h ; ) ^ final( ; ) } d u. F h ^ = data = meas. first guess = misfit = representer coefficients Key: Physical Space / user supplied Both / Auto-generated Data Space/IOM supplied Subroutine Notation: foo( in ; out ) Pure Data Space…

IOM First Guess Code first(; u. F){ read F tanlin( F(x, t) ; UF(x, t) ) measure(UF(x, t) ; u. F) } F(x, t) = Initial / boundary / interior forcing UF(x, t) = response to F u. F = measured first guess

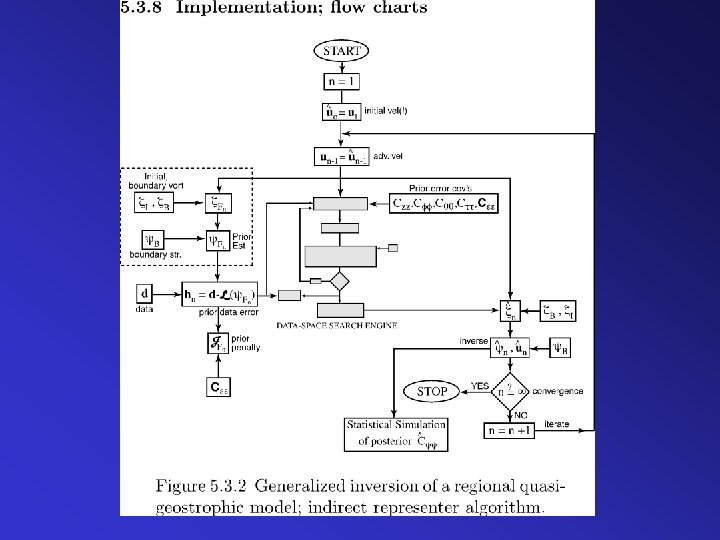
IOM Inner Solver Code solve(h ; ^ ){ =h while ( ≠ ){ comb( ; D(x, t) ) adjoint( D(x, t) ; (x, t) ) convolve( (x, t) ; (x, t) ) tanlin( (x, t) ; (x, t) ) measure( (x, t) ; ) stabilize( , ; ) call precongrad( ; ) } ^ = } (x, t) = adjoint (x, t) = forward D(x, t) = Dirac comb ^ = representer coefs = measured = scratch

IOM Final Sweep ^ final( ; ){ comb(^ ; D(x, t) ) adjoint( D(x, t) ; (x, t) ) convolve( (x, t) ; (x, t) ) ^ tanlin( (x, t) + F(x, t); U(x, t) ) ^ write U(x, t) } D(x, t) = Dirac comb ^ U(x, t) = optimal estimate (x, t) = optimal adjoint

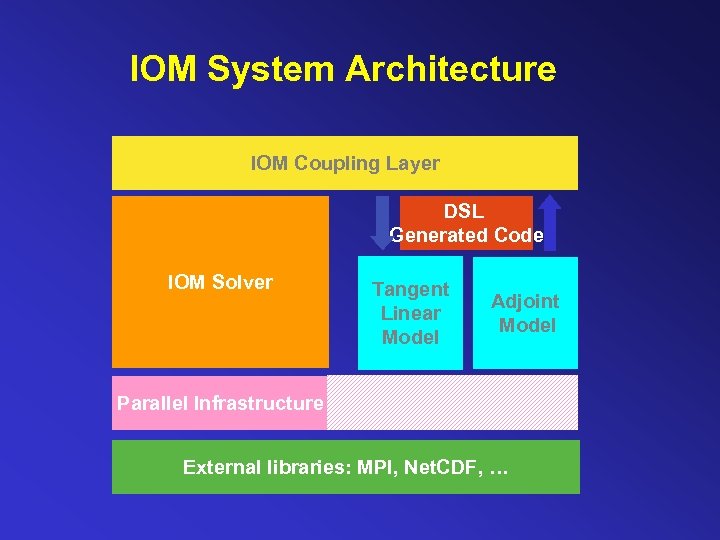IOM System Architecture IOM Coupling Layer DSL Generated Code IOM Solver Tangent Linear Model Adjoint Model Parallel Infrastructure External libraries: MPI, Net. CDF, …

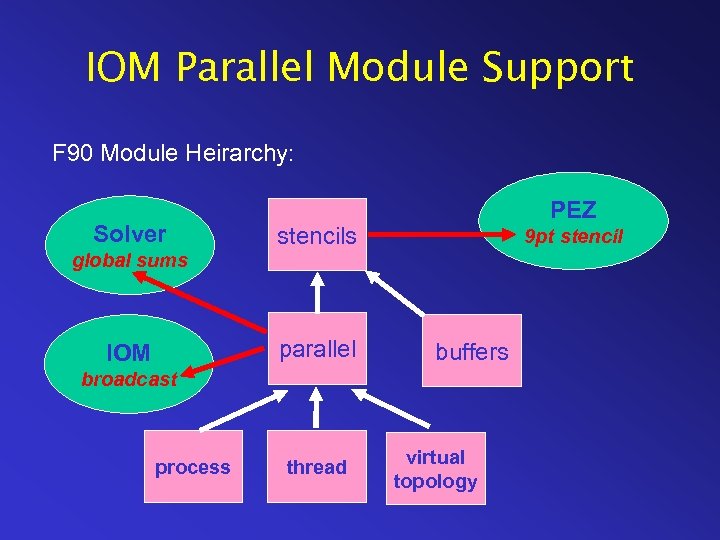IOM Parallel Module Support F 90 Module Heirarchy: Solver PEZ stencils 9 pt stencil global sums parallel IOM buffers broadcast process thread virtual topology

IOM Coupling Design Details Key object: the observation – Simplest case: a point observation – is a distribution: ( - ', t-t' ) – In general smeared out over space-time. The observation (self describing) – F 90 derived type – type of observation – units Associated methods must be supplied for mapping observations onto gridded state variables.

IOM Coupling Design Details Fortran/Unix specific (applications / code generator) Preferred mode: separate executables. – IOM + coupler + ocean models (constant functions) – IOM-PEZ components currently merged into one executable IOM supports parallel components (MPI/OMP/hybrid) Fixed number of processors – MPI_SPAWN and MPI_SPAWN_MULTIPLE not supported on many major platforms (e. g. IBM) ). Coupled component execution does not overlap. – Strategy adopted to enable easy interfacing with diverse ocean codes, with different internal forms of parallelism. Solver checkpoint/restarts IOM system, no internal state savedon TLM/ adjoint model side.

Automatic Generation of Model. Specific IOM Tools Martin Erwin and Zhe Fu Oregon State University Idea: • Specify ocean modeling tools once • Identify model-dependent parameters • Generate Fortran programs from specification and values for parameters Ocean modelers: • select simulation tools • provide parameters for their models • obtain a customized variational system

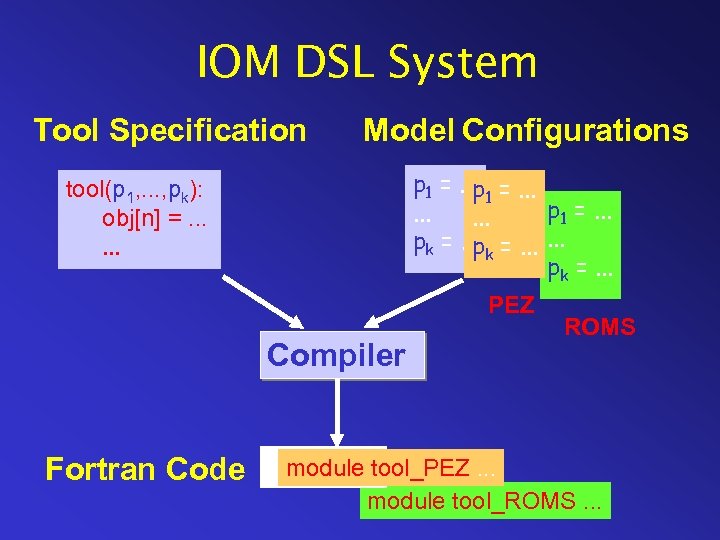IOM DSL System Tool Specification Model Configurations p 1 =. . . p p 1 =. . pk =. . . p pk =. . . tool(p 1, . . . , pk): obj[n] =. . . PEZ Compiler Fortran Code ROMS module tool_PEZ. . . module tool_ROMS. . .

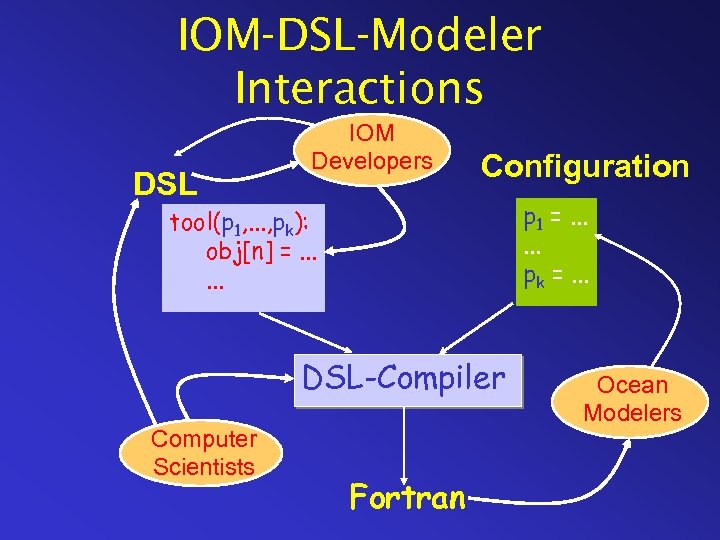IOM-DSL-Modeler Interactions DSL IOM Developers Configuration p 1 =. . . pk =. . . tool(p 1, . . . , pk): obj[n] =. . . DSL-Compiler Computer Scientists Fortran Ocean Modelers

Questions?