f99b92f3d8e12c1f25f4433d9c07f37a.ppt
- Количество слайдов: 20

Costs and Benefits The importance of marginalism

Maximizing net benefit • Slogans: – “Greatest good of the greatest number” – “Do it if the benefits outweigh the costs” – “Maximize benefits and minimize costs” Are imprecise guides to economic decisions whose goal is to maximize economic surplus or net benefit.

Comparing costs and benefits • Net benefit = Total Benefits - Total Costs • To maximize NET benefits, find the level of an activity at which MARGINAL COSTS = MARGINAL BENEFITS (or as close to equality as the problem permits)

MC = MB leads to UNIQUE solution • Marginal costs = marginal benefits will lead to the unique optimal decision. • Total Benefit > Total Cost will NOT lead to a unique solution. Since both benefits and costs will normally rise with the level of an activity, many possible levels have total benefits greater than total costs. • But since marginal costs normally rise and marginal benefits normal decline, there will be one level of an activity at which MC = MB.

MC = MB is easy to apply • Marginal costs = marginal benefits can be applied more easily than any other rule. • Maximizing Total Benefit - Total Cost by exhaustive calculation requires knowing all the costs and benefits before taking any decision. Outside of textbooks, we rarely know this. • The equimarginal principle can be applied in stages: if MB > MC at a given level of activity, increase the activity; if MB < MC, decrease the activity; if MB = MC, stop.

Umbrellas and utility http: //www. geocities. com/oldiesgg/singingin. mid Click above for the title song

Example: how many umbrellas? (umbrellas cost $5 each; declining marginal benefit) Umbrellas Tot. Benefit Tot. Cost 0 0 0 1 40 5 2 60 10 3 75 15 4 85 20 5 90 25 6 93 30 Surplus
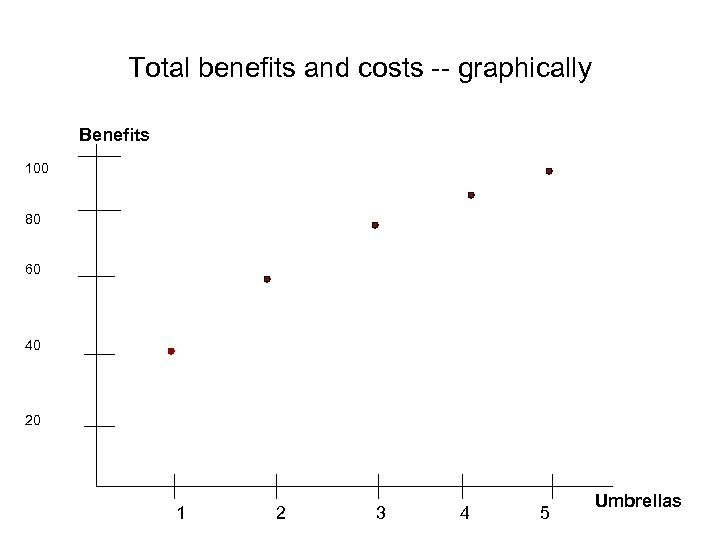
Total benefits and costs -- graphically Benefits 100 80 60 40 20 1 2 3 4 5 Umbrellas
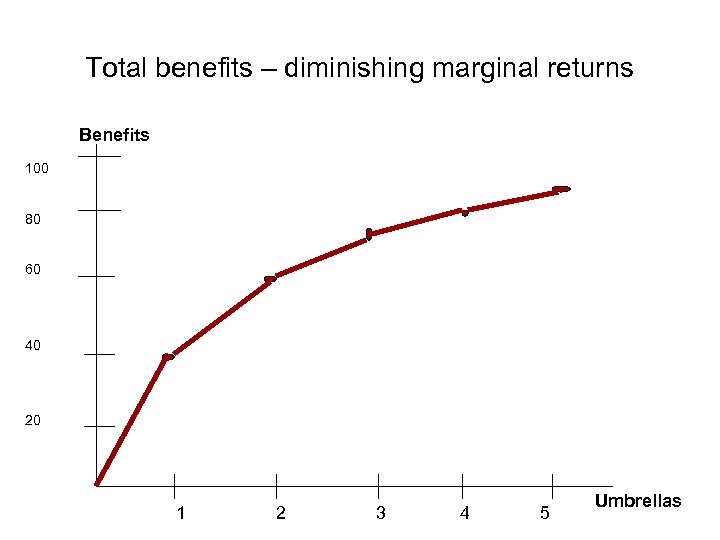
Total benefits – diminishing marginal returns Benefits 100 80 60 40 20 1 2 3 4 5 Umbrellas
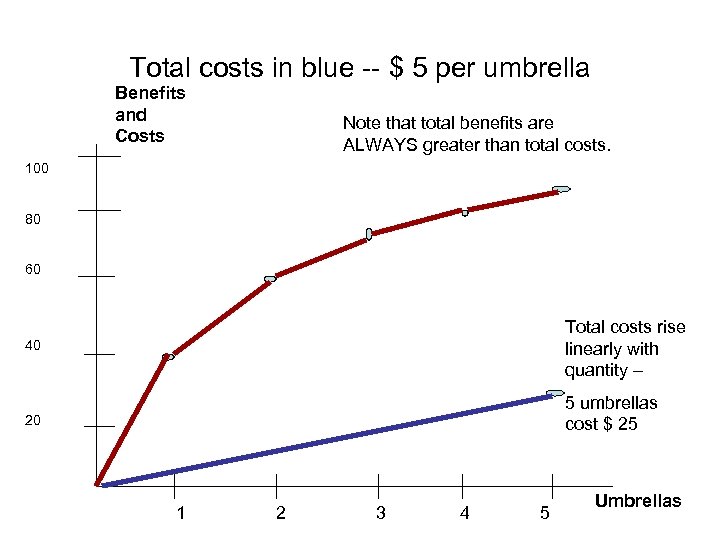
Total costs in blue -- $ 5 per umbrella Benefits and Costs Note that total benefits are ALWAYS greater than total costs. 100 80 60 Total costs rise linearly with quantity – 40 5 umbrellas cost $ 25 20 1 2 3 4 5 Umbrellas

Example: how many umbrellas? (direct computation eventually leads to the answer: you maximize surplus with 4 or 5 umbrellas ) Umbrellas Tot. Benefit Tot. Cost Surplus 0 0 1 40 5 35 2 60 10 50 3 75 15 60 4 85 20 65 5 90 25 65 ** 6 93 30 63

Example: how many umbrellas? (computing MARGINAL BENEFIT leads to the same answer as computing all net benefits) Umbrellas Tot. Benefit MB ? ? MC 0 0 ----- 1 40 40 MB > MC 2 60 20 MB > MC 3 75 15 MB > MC 4 85 10 MB > MC 5 90 5 MB = MC ** 6 93 3 MB < MC

MARGINAL = ADDITIONAL • In the last table, MARGINAL BENEFIT was computed as the difference between the benefit resulting from an additional umbrella and the benefit without the additional umbrella. • For example, MB at 4 umbrellas is equal to Total Benefit at 4 minus Total Benefit at 3 or 85 – 75 = 10.
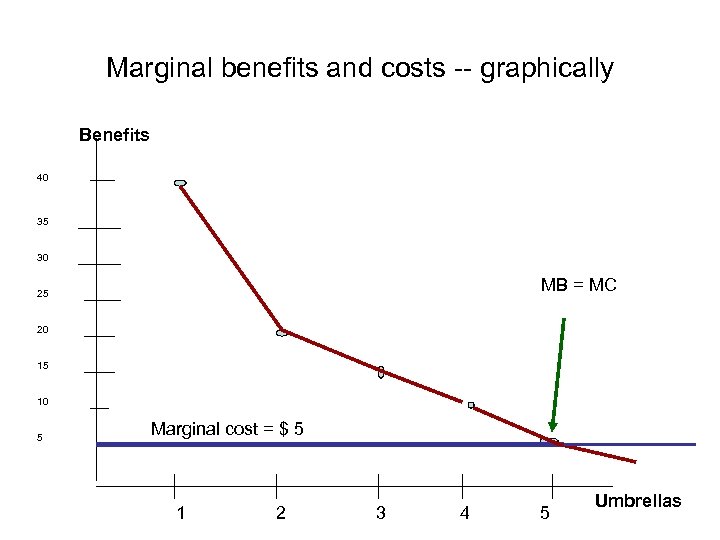
Marginal benefits and costs -- graphically Benefits 40 35 30 MB = MC 25 20 15 10 5 Marginal cost = $ 5 1 2 3 4 5 Umbrellas

Advantages of marginalism • Step-by-step procedure: even if we did not know all the costs and benefits, we can take another step (increase the level of activity) as long as MB > MC. “How much would you be willing to pay for 5 umbrellas? ” is a hard question to answer; “How much would you pay for another umbrella? ” is an easier question to answer. • Faster “what-if? ” recalculations. What if the price of umbrellas were $8? $15? Using the “total benefit” method requires every calculation to be repeated; but we could read the result quickly from the marginal table.

Tomatoes and Diminishing Marginal Returns
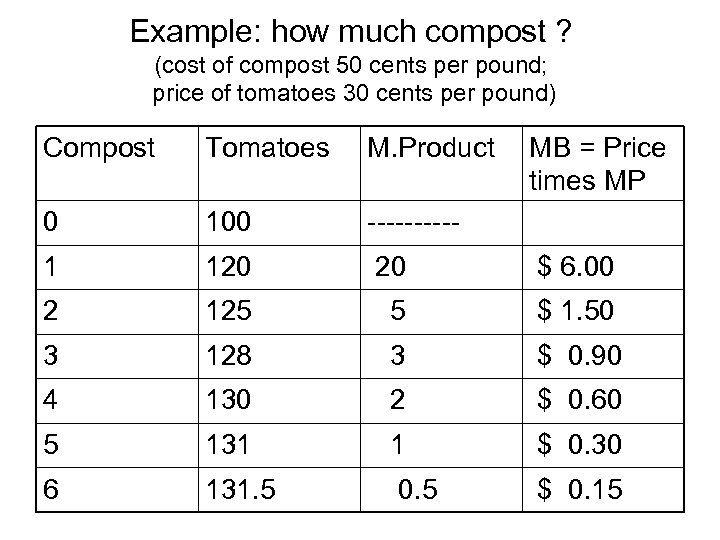
Example: how much compost ? (cost of compost 50 cents per pound; price of tomatoes 30 cents per pound) Compost Tomatoes M. Product MB = Price times MP 0 100 ----- 1 120 20 $ 6. 00 2 125 5 $ 1. 50 3 128 3 $ 0. 90 4 130 2 $ 0. 60 5 131 1 $ 0. 30 6 131. 5 0. 5 $ 0. 15

Tomatoes and compost • What if the price of compost rises to $ 1. 00 a pound? (answer: buy 2 pounds) • What if the price of tomatoes rises to 60 cents a pound (with compost at 50 cents)? Multiply marginal product by $0. 60 to get a new “marginal benefit” column; compare to the price of compost. • Compute the net benefit in the original case and the above two problems to satisfy yourself that the MB = MC rule will maximize net benefit in all cases.
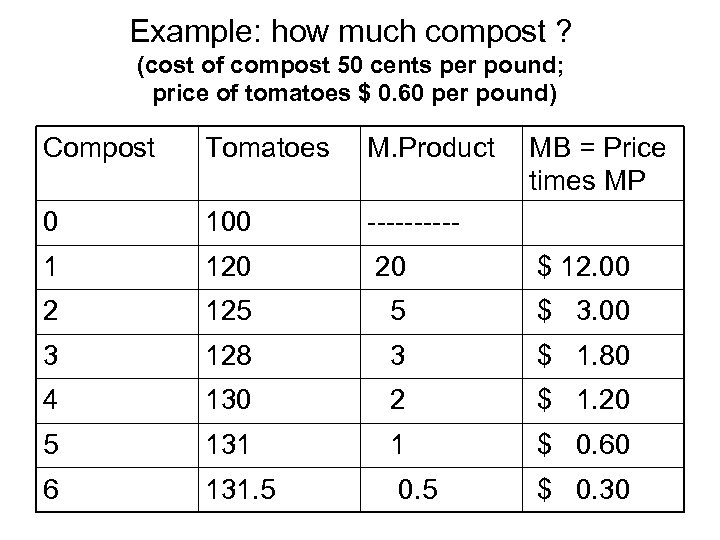
Example: how much compost ? (cost of compost 50 cents per pound; price of tomatoes $ 0. 60 per pound) Compost Tomatoes M. Product MB = Price times MP 0 100 ----- 1 120 20 $ 12. 00 2 125 5 $ 3. 00 3 128 3 $ 1. 80 4 130 2 $ 1. 20 5 131 1 $ 0. 60 6 131. 5 0. 5 $ 0. 30
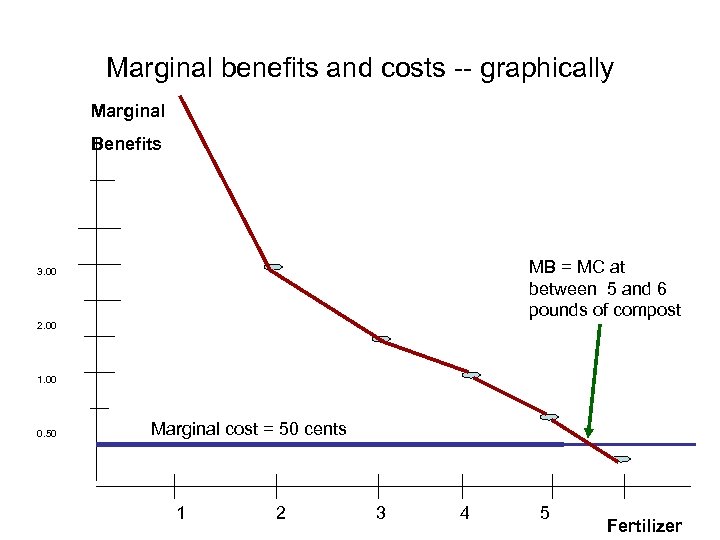
Marginal benefits and costs -- graphically Marginal Benefits MB = MC at between 5 and 6 pounds of compost 3. 00 2. 00 1. 00 0. 50 Marginal cost = 50 cents 1 2 3 4 5 Fertilizer
f99b92f3d8e12c1f25f4433d9c07f37a.ppt