COST-VOLUME-PROFIT CVP ANALYSIS Outline What is CVP

COST-VOLUME-PROFIT (CVP) ANALYSIS

Outline What is CVP analysis The importance of CVP to use in decision making Break-Even point ( BEP) Contribution Margin (CM) Contribution Margin Ratio (CMR) Target Profit Safety Margin CVP Analysis with single Product What Is Sales Mix CVP Analysis with Multiple Products Assumptions of CVP Analysis Limitation of CVP

What is CVP analysis The cost-volume-profit study is the manner of how to evolve the total revenues, the total costs and operating profit, as changes occur in volume production, sale price, the unit variable cost and / or fixed costs of a product.

The importance of CVP to use in decision making Managers use this analysis to answer different questions like: How will incomes and costs be affected if we still sell 1. 000 units? But if you expand or reduce selling prices? If we expand our business in foreign markets ? The cost-volume-profit is a necessary tool forecasting also for management control. Cost volume profit analysis (CVP analysis) is one of the most powerful tools that managers have at their command.

Break-Even point ( BEP) Break even point is the level of sales at which profit is zero. According to this definition, at break even point sales are equal to fixed cost plus variable cost. This concept is further explained by the following equation: [Break even sales = fixed cost + variable cost] TR-TC=Profit TR-TC=0 Where: Q= output and P=price if: (Q*P)-TFC-(Q*UVC)=0 (Q*P)-(Q*UVC)-TFC=0 Q(P-UVC)=TFC Q=TFC/P-UVC

Assumption of (BEP) The Break-even Analysis depends on three key assumptions: Average per-unit sales price (per-unit revenue) Average per-unit cost Monthly fixed costs

Break-Even point ( BEP) To calculate the BEP Equation two Methods are used : A) equation method B) Contribution Margin Method

equation method The format of this method can be expressed in equation form as follows: [Profit = (Sales − Variable expenses) − Fixed expenses] Rearranging this equation slightly yields the following equation, which is widely used in cost volume profit (CVP) analysis: [Sales = Variable expenses + Fixed expenses + Profit]

Break-Even point (Equation Method) Q = 350 Units

Contribution Margin The contribution margin is total revenue minus total variable costs. Similarly, the contribution margin per unit is the selling price per unit minus the variable cost per unit. Both contribution margin and contribution margin per unit are valuable tools when considering the effects of volume on profit. Contribution margin per unit tells us how much revenue from each unit sold can be applied toward fixed costs. Once enough units have been sold to cover all fixed costs, then the contribution margin per unit from all remaining sales becomes profit. [Contribution Margin = Sales revenue − Variable cost ] CM=P-VC

Contribution Margin method (cont’d) ABC company Note: For each additional product X sold, the company will generate $400 in contribution margin.

Contribution Margin method (cont’d) We can use CM method to find the BEP (in units)= FC/UCM $160, 000/$400= 400 units of product X

Contribution Margin Ratio The contribution margin as a percentage of total sales is referred to as contribution margin ratio (CM Ratio). Formula or equation of CM ratio is as follows: [ CM Ratio = Contribution Margin / Sales ] Therefore in our example: CMR= 160, 000/400, 000= 0. 4 0 r 40%

The Importance of (CMR) The CM ratio is extremely useful since it shows how the contribution margin will be affected by a change in total sales. To illustrate notice that in our example has a CM ratio of 40%. This means that for each dollar increase in sales, total contribution margin will increase by 40 cents ($1 sales × CM ratio of 40%). Net operating income will also increase by 40 cents, assuming that fixed cost do not change.

Break- Even Point in sales Formula: FC/ CMR Therefore : 160, 000/40% = $400, 000 sales

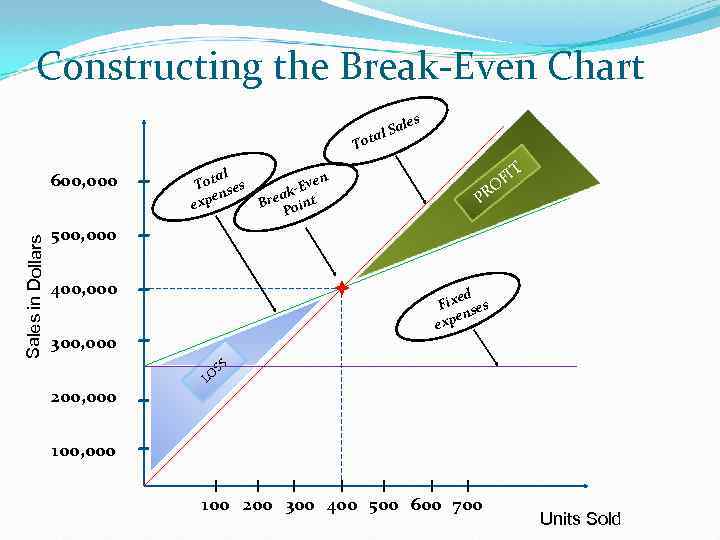Constructing the Break-Even Chart Tot P Sales in Dollars T FI O PR it al en Tot ses -Ev ak en Bre oint exp P ro f 600, 000 es al al S 500, 000 400, 000 ed Fix ses en exp 300, 000 200, 000 SS O L 100, 000 100 200 300 400 500 600 700 Units Sold

Target Profit analysis Question: How many units of product X should be produced and soled to reach a profit of $ 200, 000 ? Formula: Units sold to earn the target profit : Q= FC + Target Profit/UCM Therefore in ABC company : 160, 000+200, 000/ 400= 900 units

Margin of safety (MOS) Margin of safety (MOS): is the excess of budgeted or actual sales over the break even volume of sales. It stats the amount by which sales can drop before losses begin to be incurred. The higher the margin of safety, the lower the risk of not breaking even. Formula: [Margin of Safety = Total budgeted or actual sales − Break even sales] The margin of safety can also be expressed in percentage form. [MOS = Margin of safety in dollars / Total budgeted or actual sales]

Margin of safety (MOS) Cont’d Example: The company has a BEP of $400, 000. If actual sales are $1000, 000 the safety margin is: 1000, 000 -400, 000= $600, 000 or 600 units of product X OR: 600, 000/1000, 000= 60% Margin of safety as a percentage of sales

CVP Analysis with Multiple Products Sale mix: Definition and Explanation of the Concept: The term sale mix refers to the relative proportion in which a company's products are sold. The concept is to achieve the combination, that will yield the greatest amount of profits. Most companies have many products, and often these products are not equally profitable. Hence, profits will depend to some extent on the company's sales mix. Profits will be greater if high margin rather than low margin items make up a relatively large proportion of total sales.

Sales Mix and Break Even Analysis: If a company sells multiple products, break even analysis is somewhat more complex . The reason is that the different products will have different selling prices, different costs, and different contribution margins. Consequently, the break even point will depend on the mix in which the various products are sold.

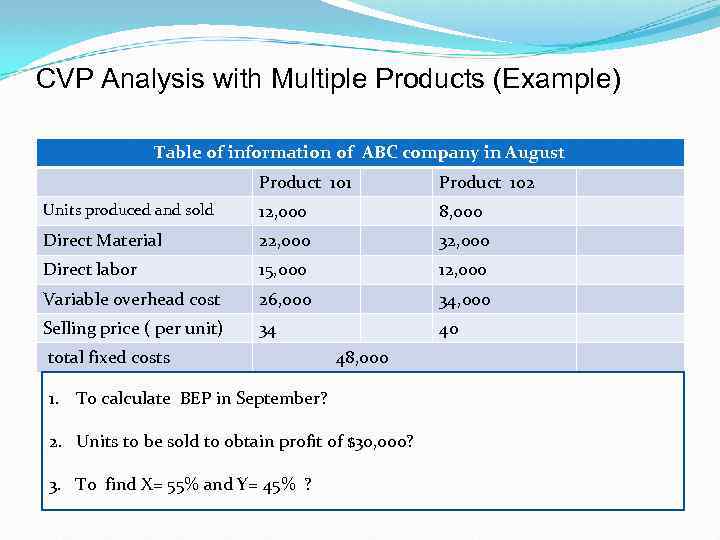CVP Analysis with Multiple Products (Example) Table of information of ABC company in August Product 101 Product 102 Units produced and sold 12, 000 8, 000 Direct Material 22, 000 32, 000 Direct labor 15, 000 12, 000 Variable overhead cost 26, 000 34, 000 Selling price ( per unit) 34 40 total fixed costs 48, 000 1. To calculate BEP in September? 2. Units to be sold to obtain profit of $3 o, ooo? 3. To find X= 55% and Y= 45% ?

CVP Analysis with Multiple Products (Example) cont’d (1) Formula of BEP in multiple products: BEP=total FC/WAUCM UVC(X)=22, 000+15, 000+26, 000/12, 000=5. 25 UVC(Y)= 32, 000+ 12, 000+34, 000/8, 000=9. 75 UCM= P-UVC UCM(X)= 34 -5. 25 =28. 75 UCM(Y)=40 -9. 75 =30. 25 12, 000+8000=20, 000 WAUCM =UCM* % of total 12, 000/20, 000= 0. 6 WAUCM(X)= 28. 75*60%=17. 25 8, 000/20, 000= 0. 4 WAUCM(Y)=30. 25*40%= 12. 1 total of sales mix 29. 35

CVP Analysis with Multiple Products (Example) cont’d BEP=total FC/WAUCM BEP=48, 000/ 29. 35=1635. 5 X=1635. 5 *0. 6= 981 units Y=1635. 5 *0. 4= 654 units (2) Units to be sold to obtain $3 o, ooo? BEP=total FC+P/WAUCM BEP=48, 000+ 30, 000/ 29. 35=2, 657 X=2, 675*0. 6=1, 605 units Y=2, 675*0. 4=1070 units

CVP Analysis with Multiple Products (Example) cont’d (3) X= 55% and Y= 45% ? 28. 75*55% =15. 8 30. 25*45%= 13. 6 total of sales mix 29. 4 BEP=total FC/WAUCM 48, 000/29. 4=1632 1632*55%=897 units 1632*45%=734 units

cost volume profit analysis assumptions 1. All costs can be analysed into their fixed and variable elements. 2. Fixed costs remain fixed even over a wide range of activity. 3. Variable costs always vary directly with activity. 4. Selling prices are constant per unit. 5. Only levels of activity affect costs and revenues 6. usually one product can be effectively dealt with 7. Uncertainty does not exist.

Limitations of Cost-Volume-Profit (CVP) Analysis: Cost volume profit (CVP) is a short run, marginal analysis: it assumes that unit variable costs and unit revenues are constant, which is appropriate for small deviations from current production and sales, and assumes a neat division between fixed costs and variable costs, though in the long run all costs are variable. For longerterm analysis that considers the entire life-cycle of a product, one therefore often prefers activity-based costing or throughput accounting.