Cost Management ACCOUNTING AND CONTROL HANSEN MOWEN

Cost Management ACCOUNTING AND CONTROL HANSEN & MOWEN 1

17 Cost-Volume-Profit Analysis 2

1 The Break-Even Point in Units Sales (72, 500 units @ $40) Less: Variable expenses Contribution margin Less: Fixed expenses Operating income $2, 900, 000 1, 740, 000 $1, 160, 000 800, 000 $ 360, 000 3

1 The Break-Even Point in Units Operating Income Approach 0 = ($40 x Units) – ($24 x Units) – $800, 000 0 = ($16 x Units) – $800, 000 ($16 x Units) = $800, 000 Units = 50, 000 $1, 740, 000 ÷ 72, 500 Proof Sales (50, 000 units @ $40) Less: Variable expenses Contribution margin Less: Fixed expenses Operating income $2, 000 1, 200, 000 $ 800, 000 $ 0 4

The Break-Even Point in Units 1 Contribution Margin Approach Number of units = $800, 000 / ($40 - $24) = $800, 000 / $16 per unit = 50, 000 units 5

1 The Break-Even Point in Units Target Income as a Dollar Amount $424, 000 = ($40 x Units) – ($24 x Units) – $800, 000 $1, 224, 000 = $16 x Units = 76, 500 Proof Sales (76, 500 units @ $40) Less: Variable expenses Contribution margin Less: Fixed expenses Operating income $3, 060, 000 1, 836, 000 $1, 224, 000 800, 000 $ 424, 000 6

The Break-Even Point in Units 1 Target Income as a Percentage of Sales Revenue More-Power Company wants to know the number of sanders that must be sold in order to earn a profit equal to 15 percent of sales revenue. 0. 15($40)(Units) = ($40 x Units) – ($24 x Units) – $800, 000 $6 x Units = ($16 x Units) – $800, 000 $10 x Units = $800, 000 Units = 80, 000 7

The Break-Even Point in Units 1 After-Tax Profit Targets Net income = Operating income – Income taxes = Operating income – (Tax rate x Operating income) = Operating income (1 – Tax rate) Or Operating income = Net income (1 – Tax rate) 8

The Break-Even Point in Units 1 After-Tax Profit Targets More-Power Company wants to achieve net income of $487, 500 and its income tax rate is 35 percent. $487, 500 = Operating income – 0. 35(Operating income) $487, 500 = 0. 65(Operating income) $750, 000 = Operating income Units = ($800, 000 + $750, 000)/$16 Units = $1, 550, 000/$16 Units = 96, 875 9

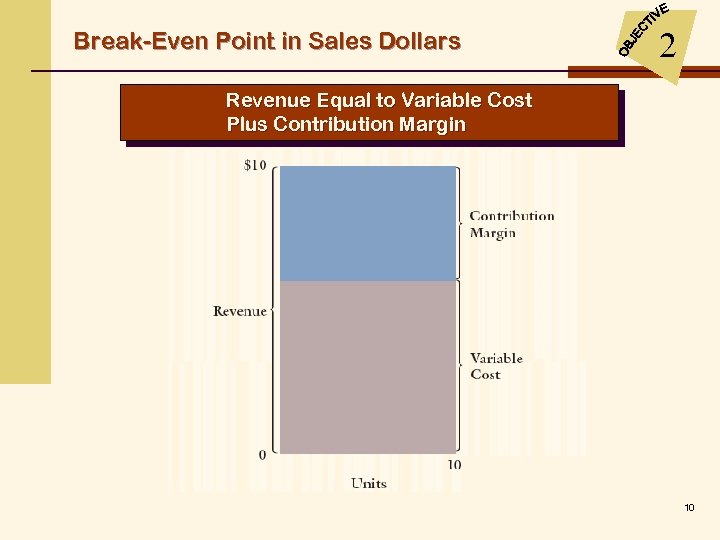Break-Even Point in Sales Dollars 2 Revenue Equal to Variable Cost Plus Contribution Margin 10

2 Break-Even Point in Sales Dollars The following More-Power Company To determine the break-even in sales dollars, the contribution margin income statement is margin ratio must be determined ($1, 160, 000 ÷ $2, 900, 000). shown for sales of 72, 500 sanders. Sales Less: Variable expenses Contribution margin Less: Fixed expenses Operating income $2, 900, 000 100% 1, 740, 000 60% $1, 160, 000 800, 000 $ 360, 000 40% 11

Break-Even Point in Sales Dollars 2 Operating income = Sales – Variable costs – Fixed Costs 0 = Sales – (Variable cost ratio x Sales) – Fixed costs 0 = Sales (1 – Variable cost ratio) – Fixed costs 0 = Sales (1 –. 60) – $800, 000 Sales(0. 40) = $800, 000 Sales = $2, 000 12

Break-Even Point in Sales Dollars 2 Impact of Fixed Costs on Profit 13

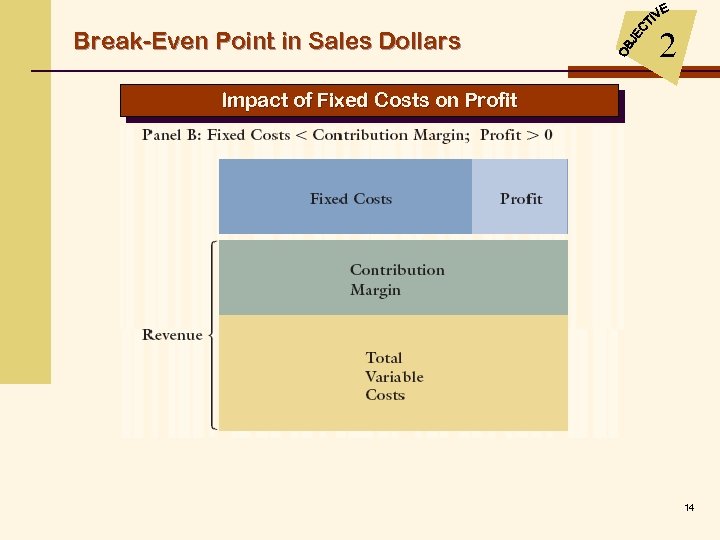Break-Even Point in Sales Dollars 2 Impact of Fixed Costs on Profit 14

Break-Even Point in Sales Dollars 2 Impact of Fixed Costs on Profit 15

Break-Even Point in Sales Dollars 2 Profit Targets How much sales revenue must More-Power generate to earn a before-tax profit of $424, 000? Sales = ($800, 000) + $424, 000/0. 40 = $1, 224, 000/0. 40 = $3, 060, 000 16

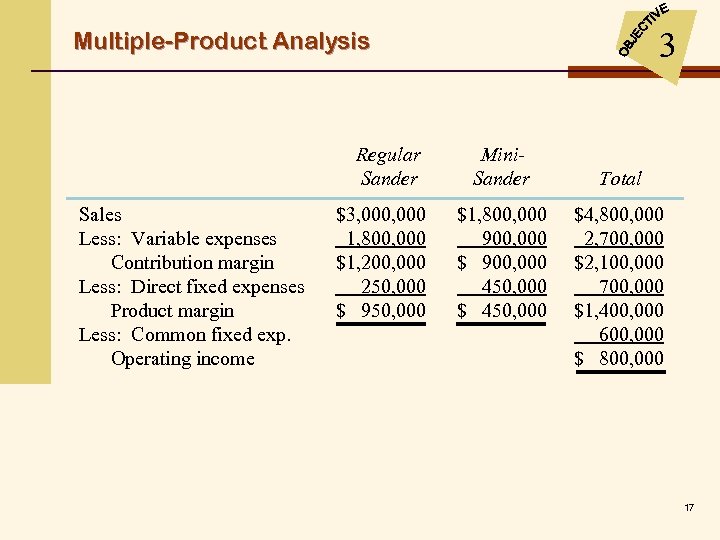3 Multiple-Product Analysis Regular Sander Sales Less: Variable expenses Contribution margin Less: Direct fixed expenses Product margin Less: Common fixed exp. Operating income $3, 000 1, 800, 000 $1, 200, 000 250, 000 $ 950, 000 Mini. Sander $1, 800, 000 900, 000 $ 900, 000 450, 000 $ 450, 000 Total $4, 800, 000 2, 700, 000 $2, 100, 000 700, 000 $1, 400, 000 600, 000 $ 800, 000 17

Multiple-Product Analysis 3 Regular sander break-even units = Fixed costs/(Price – Unit variable cost) = $250, 000/$16 = 15, 625 units Mini-sander break-even units = Fixed costs/(Price – Unit variable cost) = $450, 000/$30 = 15, 000 units 18

Multiple-Product Analysis 3 Income Statement: Break-Even Solution 19

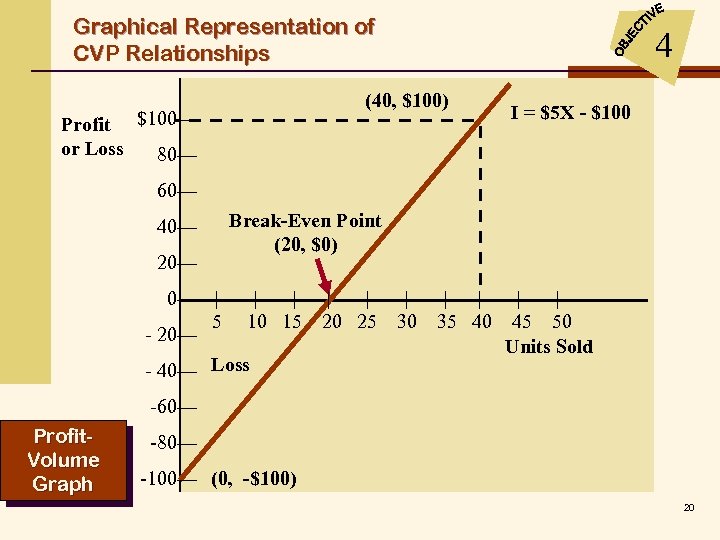Graphical Representation of CVP Relationships 4 (40, $100) Profit $100— or Loss 80— I = $5 X - $100 60— 40— 20— 0— | 5 - 20— Break-Even Point (20, $0) | | 10 15 - 40— Loss | | 20 25 | 30 | | 35 40 | | 45 50 Units Sold -60— Profit. Volume Graph -80— -100— (0, -$100) 20

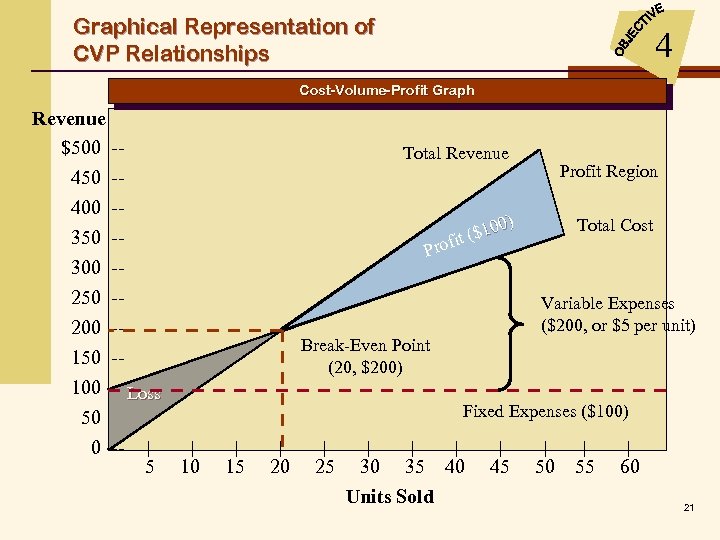Graphical Representation of CVP Relationships 4 Cost-Volume-Profit Graph Revenue $500 -450 -400 -350 -300 -250 -200 -150 -100 -- Loss 50 -| 0 -- | 5 10 Total Revenue Profit Region 0) $10 it ( Total Cost Prof Variable Expenses ($200, or $5 per unit) Break-Even Point (20, $200) Fixed Expenses ($100) | 15 | 20 | 25 | | | 30 35 40 Units Sold | 45 | 50 | 55 | 60 21

Graphical Representation of CVP Relationships 4 Assumptions of C-V-P Analysis 1. The analysis assumes a linear revenue function and a linear cost function. 2. The analysis assumes that price, total fixed costs, and unit variable costs can be accurately identified and remain constant over the relevant range. 3. The analysis assumes that what is produced is sold. 4. For multiple-product analysis, the sales mix is assumed to be known. 5. The selling price and costs are assumed to be known with certainty. 22

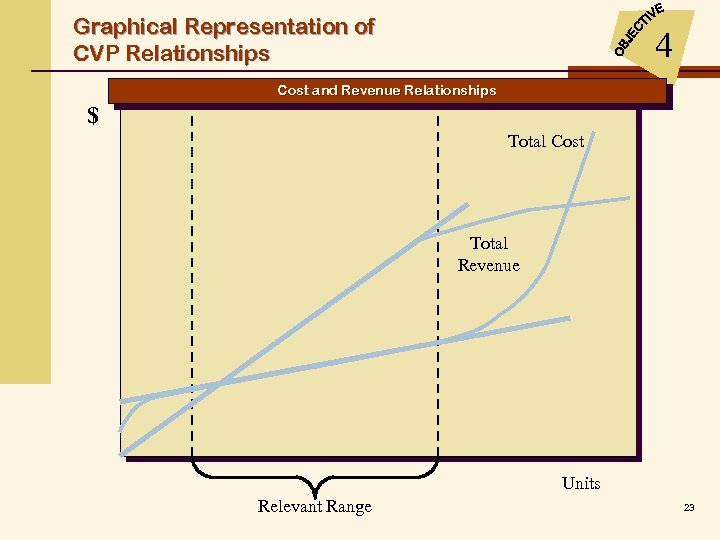Graphical Representation of CVP Relationships 4 Cost and Revenue Relationships $ Total Cost Total Revenue Units Relevant Range 23

Changes in the CVP Variables 5 Alternative 1: If advertising expenditures increase by $48, 000, sales will increase from 72, 500 units to 75, 000 units. Summary of the Effects of the First Alternative 24

Changes in the CVP Variables 5 Alternative 2: A price decrease from $40 per sander to $38 would increase sales from 72, 500 units to 80, 000 units. Summary of the Effects of the Second Alternative 25

Changes in the CVP Variables 5 Alternative 3: Decreasing price to $38 and increasing advertising expenditures by $48, 000 will increase sales from 72, 500 units to 90, 000 units. Summary of the Effects of the Third Alternative 26

5 Changes in the CVP Variables Margin of Safety Assume that a company has a break-even volume of 200 units and the company is currently selling 500 units. Current sales Break-even volume Margin of safety (in units) Break-even point in dollars: Current revenue Break-even volume Margin of safety (in dollars) 500 200 300 $350, 000 200, 000 $150, 000 27

5 Changes in the CVP Variables Operating Leverage Automated System Sales (10, 000 units) Less: Variable expenses Contribution margin Less: Fixed expenses Operating income Unit selling price Unit variable cost Unit contribution margin Manual System $1, 000 500, 000 $ 500, 000 375, 000 $ 125, 000 $1, 000 800, 000 $ 200, 000 100, 000 $100 $500, 00050 ÷ $125, 00050 = DOL of 4 $100 $200, 000 ÷ 80 $200, 000 = 20 DOL of 2 28

Changes in the CVP Variables 5 What happens to profit in each system if sales increase by 40 percent? 29

5 Changes in the CVP Variables Automated System Sales (14, 000 units) Less: Variable expenses Contribution margin Less: Fixed expenses Operating income $1, 400, 000 700, 000 $ 700, 000 375, 000 $ 325, 000 Manual System $1, 400, 000 1, 120, 000 $ 280, 000 100, 000 $ 180, 000 Manual system— 40% x 2 = 80% Automated system— 40% x 4 = 160% $100, 000 x 80% = $80, 000 $125, 000 x 160% = $200, 000 increase $100, 000 + $80, 000 = $180, 000 $125, 000 + $200, 000 = $325, 000 30

CVP Analysis and Activity-Based Costing 6 The ABC Cost Equation Total cost = Fixed costs + (Unit variable cost x Number of units) + (Setup cost x Number of setups) + (Engineering cost x Number of engineering hours) Operating Income Operating income = Total revenue – [Fixed costs + (Unit variable cost x Number of units) + (Setup cost x Number of setups) + (Engineering cost x Number of engineering hours)] 31

CVP Analysis and Activity-Based Costing 6 Break-Even in Units Break-even units = [Fixed costs + (Setup cost x Number of setups) + (Engineering cost x Number of engineering hours)]/(Price – Unit variable cost) Differences Between ABC Break-Even and Convention Break-Even ü The fixed costs differ ü The numerator of the ABC break-even equation has two nonunit-variable cost terms 32

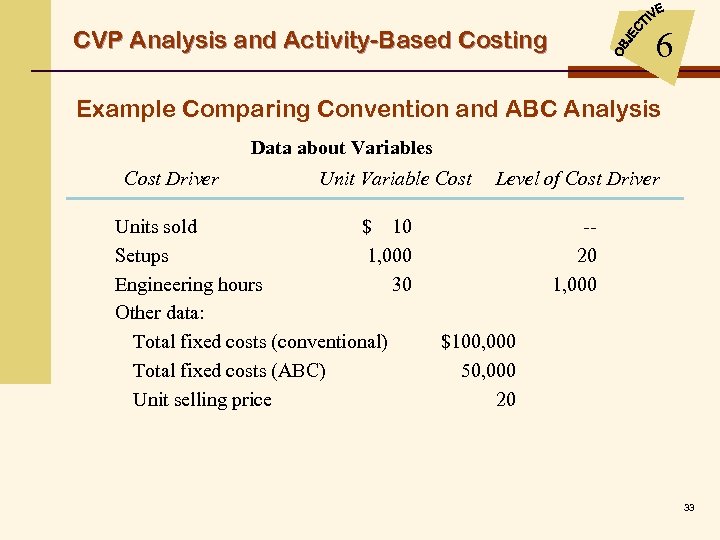6 CVP Analysis and Activity-Based Costing Example Comparing Convention and ABC Analysis Data about Variables Cost Driver Unit Variable Cost Units sold $ 10 Setups 1, 000 Engineering hours 30 Other data: Total fixed costs (conventional) Total fixed costs (ABC) Unit selling price Level of Cost Driver -20 1, 000 $100, 000 50, 000 20 33

CVP Analysis and Activity-Based Costing 6 Example Comparing Convention and ABC Analysis Units to be sold to earn a before-tax profit of $20, 000: Units = (Targeted income + Fixed costs)/(Price – Unit variable cost) = ($20, 000 + $100, 000)/($20 – $10) = $120, 000/$10 = 12, 000 units Same data using the ABC: Units = ($20, 000 + $50, 000 + $20, 000 + $30, 000/($20 – $10) = $120, 000/$10 = 12, 000 units 34

CVP Analysis and Activity-Based Costing 6 Example Comparing Convention and ABC Analysis Suppose that marketing indicates that only 10, 000 units can be sold. A new design reduces direct labor by $2 (thus, the new variable cost is $8). The new break-even is calculated as follows: Units = Fixed costs/(Price – Unit variable cost) = $100, 000/($20 – $8) = 8, 333 units 35

CVP Analysis and Activity-Based Costing 6 Example Comparing Convention and ABC Analysis The projected income if 10, 000 units are sold is computed as follows: Sales ($20 x 10, 000) Less: Variable expenses ($8 x 10, 000) Contribution margin Less: Fixed expenses Operating income $200, 000 80, 000 $120, 000 100, 000 $ 20, 000 36

CVP Analysis and Activity-Based Costing 6 Example Comparing Convention and ABC Analysis Suppose that the new design requires a more complex setup, increasing the cost per setup from $1, 000 to $1, 600. Also, suppose that the new design requires a 40 percent increase in engineering support. The new cost equation is given below: Total cost = $50, 000 + ($8 x Units) + ($1, 600 x Setups) + ($30 x Engineering hours) 37

CVP Analysis and Activity-Based Costing 6 Example Comparing Convention and ABC Analysis The break-even point using the ABC equation is calculated as follows: Units = [$50, 000 + ($1, 600 x 20) + ($30 x 1, 400)]/($20 – $8) = $124, 000/$12 = 10, 333 This is more than the firm can sell! 38

End of Chapter 17 39