COS 444 Internet Auctions Theory and Practice Spring

COS 444 Internet Auctions: Theory and Practice Spring 2009 Ken Steiglitz ken@cs. princeton. edu week 10 1

The common-value model • All buyers have the same actual value, V. • Buyers are uncertain about this value: thus not private values. Efficiency not relevant. • Buyers estimate values variously, by consulting experts, say. We say they receive “noisy signals” that are correlated with the true value. • In a popular special case, buyers receive the signals si = V + ni , where ni is a zero-mean random process common to all buyers. • We can think of real-world bidders as living in the range between IPV and common-value. week 10 2

Winner’s Curse • The paradigmatic experiment: bid on a jar of nickels • The systematic error is to fail to take into account the fact that winning may be an informative event! • A persistent violation of the beloved hypothesis of homo economicus, the rational self-interested actor. Can be considered a “cognitive illusion” week 10 3

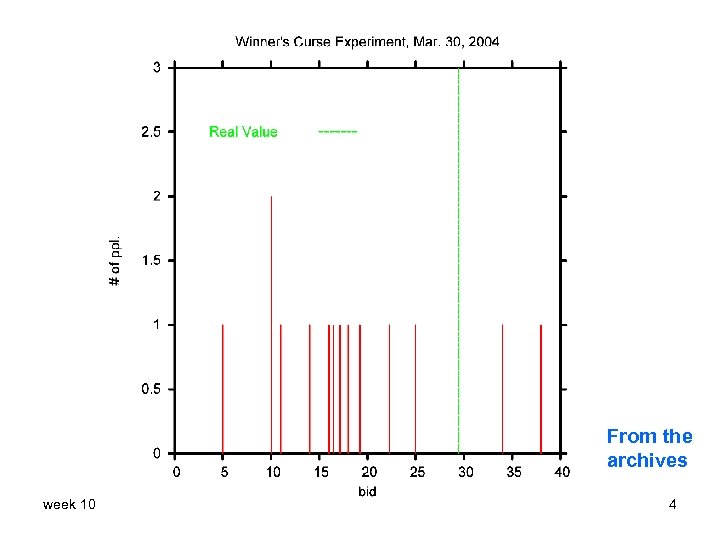From the archives week 10 4

Buy-a-Company experiment • [R. H. Thaler, The Winner’s Curse, 1992] reports the unpublished results of Weiner, Bazerman, & Carroll, 1987 with Bidding for Paramount. • 69 NWU MBA students played the game 20 rounds each, with financial incentives and feedback after each trial. 5 learned to bid ≤ $1 by end, after avg. of 8 trials No sign of learning among the others! week 10 5

Winner’s Curse, references • Seminal paper: E. C. Capen, R. V. Clapp, W. M. Campbell, “Competitive bidding in high -risk situations, ” J. Petroleum Technology, 23, 1971, pp. 641 -653. See: R. Thaler, The Winner’s Curse: Paradoxes and Anomalies of Economic Life, Princeton Univ. Press, 1992. J. H. Kagel and D. Levin, Common value auctions and the Winner’s curse, Princeton Univ. Press, 2002. week 10 6

Claims of Winner’s Curse in the field • Oil industry • Book publication rights • Professional baseball free-agent market [Blecherman & Camerer 96] • • • Corporate takeover battles Real-estate auctions Stock market investments, IPOs Blind bidding by movie exhibitors Construction industry … etc. … but difficult to prove using field data because of the existence other factors week 10 7

• What do you do if you find your competitors are making consistent errors? week 10 8

• What do you do if you find your competitors are making consistent errors? Publish. Share your knowledge. --- this lowers bids! [Thaler, pp. 61 -62, after Julia Grant] week 10 9

• What do you do if you find your competitors are making consistent errors? Publish. Share your knowledge. --- this lowers bids! [Thaler, pp. 61 -62, after Julia Grant] • When to share information and when to hide it? week 10 10

First laboratory experiment M. H. Bazerman and W. F. Samuelson, “I won the auction but I don’t want the prize, ” J. Conflict Resolution, 27, pp. 618 -34, 1983. • M. B. A. students, Boston University • Four first-price sealed-bid auctions • 800 pennies; 160 nickels; 200 large paper clips @ 4¢; 400 small paper clips @ 2¢. All thus worth V = $8. 00. week 10 [Kagel & Levin 02] 11

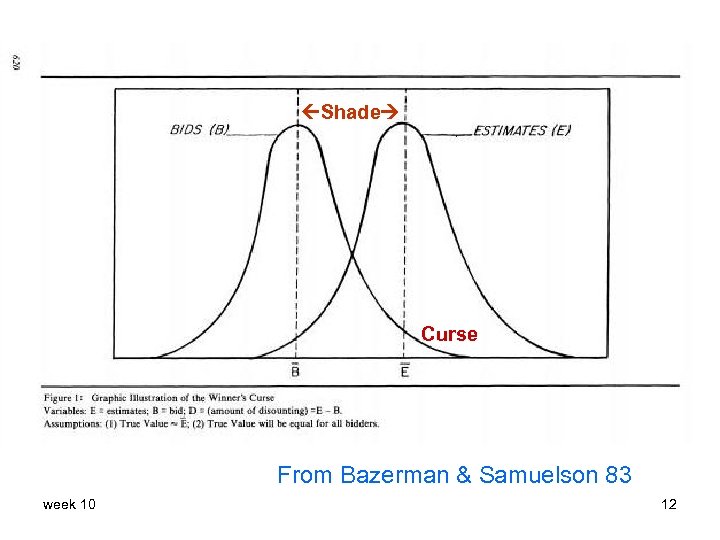Shade Curse From Bazerman & Samuelson 83 week 10 12

Bazerman and Samuelson 83 • Bidders were asked for estimates as well as bids. 48 auctions were run altogether. • Average estimate was $5. 13 = $8 – $2. 87 • Average winning bid was $10. 01 = $8 + $2. 01 • The experimental design was sophisticated, subjects were told they were competing against different numbers of bidders, and the effects of uncertainty and group size measured week 10 [Kagel & Levin 02] 13

Winning may be bad news, unless you shade appropriately • Suppose bidders are uncertain about their values vi , receiving noisy signals si • Based on this information, your best estimate of your true value, after receiving the signal si=x, is E[V | s 1=x ] • Suppose you, bidder 1, win the auction! • Then your new best estimate of your value is E[V | s 1=x , Y 1 < x ] < E[V | s 1=x ] --- where Y 1 is the highest of the other signals week 10 Intuitive argument: [Krishna 02]. Conditions for proof? 14

In first-price auctions Suppose n = number of bidders increases. • According to the private-value equilibrium, you should increase your bid • Taking into account the Winner’s Curse, you should decrease your bid (effect can dominate). Having the highest estimate among 5 bidders is not as bad as among 50. Note that in any common-value auction, the winner’s curse results from a miscalculation, and does not occur in equilibrium… so what is that equilibrium? week 10 15

Winner’s curse, con’t Important paper, which describes how to find a symmetric equilibrium in one general setting: R. B. Wilson, “Competitive Bidding with Disparate Information, ” Management Science 15, 7, March 1969, pp. 446 -448. That is, how to compensate for the tendency to forget how likely it is for winning to be bad news, in equilibrium. week 10 16

Example: FP common-value, uncorrelated signals* • Take the simple 2 -bidder example where the true value of a tract is V = v 1+ v 2 , where v 1 , v 2 = amount of oil on parts 1, 2 of a tract. Bidder i knows vi with certainty, but not the other. The vi’s are uniform iid on [0, 1]. • What is the equilbrium bid? Is it a “good” bid? How does this FP auction compare to the corresponding SP for the seller’s revenue? *From F. M. Menezes & P. K. Monteiro, An Intro. to Auction Theory, Oxford Univ. Press, 2005. week 10 17

Winning may be bad news: example • In this common-value model: V = v 1 + v 2 • E[V | v 1 ] = v 1 + ½ • E[V | v 1 & (v 2 ≤ v 1) ] = v 1 + E[v 2 | v 2 ≤ v 1 ] = v 1 + v 1 /2 ≤ v 1 + ½ = E[V | v 1 ] week 10 18

Example: FP common-value, uncorrelated signals [Menezes & Monteiro 05] • We’ll look for a symmetric, differentiable, and increasing equil. bidding fctn. b(v). As usual, suppose bidder 1 bids as if her value is z. Her expected surplus (profit) is • The equilibrium condition is week 10 19

Example: FP common-value, uncorrelated signals [Menezes & Monteiro 05] • This differential equation is of a familiar, linear type: • Integrate from 0 to v, letting b(0) = b 0. Note: we can’t assume b 0 = 0 … Why not? • Argue from finiteness of b(0) that c= 0. … So week 10 20

Example: FP common-value, uncorrelated signals [Menezes & Monteiro 05] • Notice that bidder i never pays more than the true value V. . • But now suppose signals vi are distributed as F on [0, 1], instead of being uniform. Exactly the same procedure gets us the symmetric equilibrium […is this always increasing? ] • Take the special case F = vθ , where θ > 0. week 10 21

Example: FP common-value, uncorrelated signals [Menezes & Monteiro 05] • The symmetric equilibrium then becomes • If θ > 1, the winning bidder may well bid higher, and hence pay more than, the true value V. …Is this an example of the Winner’s Curse? week 10 22

Example: SP common-value, uncorrelated signals [Menezes & Monteiro 05] • In the SP auction with this common-value model, the equilibrium in the uniform case, using the same technique, is b(v) = 2 v. • This may be higher than the true value V, and the winner may very well pay more than V. In fact, she may pay more than the expected value of V conditional on having the highest bid. …What is that? Again, is this an example of the Winner’s Curse? week 10 23

Example: common-value, uncorrelated signals [Menezes & Monteiro 05] • It turns out that the FP and SP auctions with this common-value model are revenue equivalent. In fact, this is generally true for common-value cases with independent signals [Menezes & Monteiro 05, pp. 117 ff ]. • But revenue equivalence finally breaks down when the signals are correlated. week 10 24

Kagel & Levin’s Experimental work [J. H. Kagel and D. Levin, Common value auctions and the Winner’s curse, Princeton Univ. Press, 2002] • Kagel & Levin et al. did a lot of laboratory experimental work with this model: • Choose the common value x 0 from the uniform distribution uniform on [x. L, x. H], known to the bidders. The bidders are given signals drawn uniformly and independently from [xo–ε, xo+ε], where ε is known to the bidders. • The signals in this case are correlated. week 10 25

Dyer et al. ’s comparison between experienced & inexperienced bidders [D. Dyer, J. H. Kagel, & D. Levin, “A Comparison of Naïve & Experienced Bidders in Common-Value Offer Auctions: A Laboratory Analysis, ” Econ. J. , 99, 108 -115, March 1989. ] • Experiment was a procurement auction: one buyer, many sellers, so low bid wins • Common-value model analogous to the ones in the Kagel-Levin experiments • Compares performance of Univ. Houston Econ majors with executives in local construction companies with average of 20 years experience of bid preparation week 10 26

[D. Dyer, J. H. Kagel, & D. Levin, “A Comparison of Naïve & Experienced Bidders in Common-Value Offer Auctions: A Laboratory Analysis, ” Econ. J. , 99, 108 -115, March 1989. ] Results: • Winner’s curse extends to procurement (offer) auctions • Winner’s curse extends to auctions with only 4 bidders • No significant difference in performance between undergrads and professionals! …Explain? week 10 27

Executives didn’t take the experiment seriously? Executives’ auctions in practice have a strong private -value component (overhead, opportunity costs), and losses can be mitigated by renegotiation, or changeorders? • Dyer et al. conclude, however, that “…executives have learned a set of situation specific rules of thumb which permit them to avoid the winner’s curse in the field but which could not be applied in the lab. ” (by feedback or selection) • Learning occurs “…Not through understanding and absorbing ‘the theory’, but from rules of thumb that are likely to breakdown under extreme changes, or truly novel, economic conditions. ” week 10 28

Next… • Common-value auctions lead to the next, and most general treatment of single-item auctions, Milgrom & Weber 82. • The model here is called the “affiliated values” model, and represents a spectrum, with IPV at one extreme, and common-value at the other. Most auctions have elements of both. • To wrap up the Winner’s Curse: week 10 29

Capen et al. ’s fortune cookie: “He who bids on a parcel what he thinks it is worth, will, in the long run, be taken for a cleaning. ” week 10 30

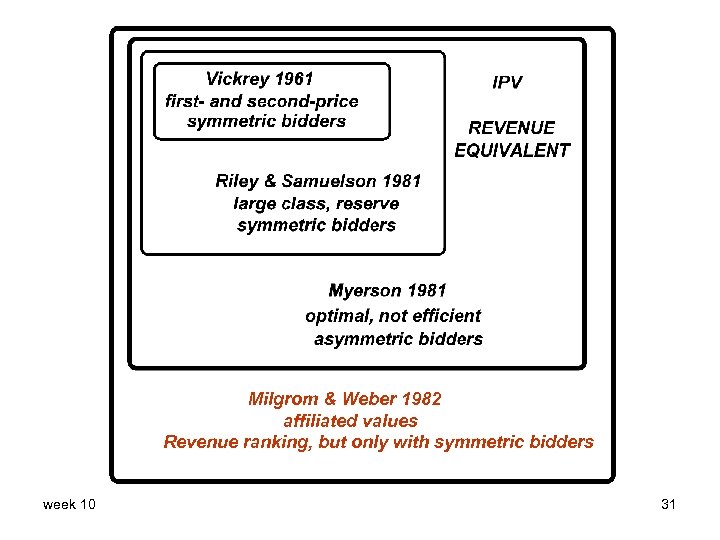Milgrom & Weber 1982 affiliated values Revenue ranking, but only with symmetric bidders week 10 31

Interdependent Values In general, we relax two IPV assumptions: • • Bidders are no longer sure of their values (as in the common-value case discussed in connection with the Winner’s Curse) Bidders’ signals are statistically correlated; technically positively affiliated (see Milgrom & Weber 82, Krishna 02) Intuitively: if some subset of signals is large, it’s more likely that the remaining signals are large week 10 32

Major results in Milgrom & Weber 82 For the general symmetric, affiliated values model: • English > 2 nd -Price > 1 st -Price = Dutch (“revenue ranking”) • If the seller has private information, full disclosure maximizes price (“Honesty is the best policy” … in the long run) week 10 33

Milgrom & Weber 82: Caveats • Symmetry assumption is crucial; results fail without it • English is Japanese button model • For disclosure result: seller must be credible, pre-committed to known policy • Game-theoretic setting assumes distributions of signals are common knowledge week 10 34

The linkage principle (after Krishna 02) Consider the price paid by the winner when her signal is x but she bids as if her value is z , and denote this price by W (z , x). Define the linkage : = sensitivity of expected price paid by winner to variations in her received signal when bid is held fixed week 10 35

The linkage principle, con’t Result: Two auctions with symmetric and increasing equilibria, and with W(0, 0) = 0, are revenue-ranked by their linkages. Consequences: 1 st -Price: linkage L 1 = 0 2 nd -Price: price paid is linked through x 2 to x 1 ; so L 2 > 0 English: … through all signals to x 1 ; so LE > L 2 > L 1 week 10 revenue ranking 36