COS 444 Internet Auctions Theory and Practice Spring

COS 444 Internet Auctions: Theory and Practice Spring 2010 Ken Steiglitz ken@cs. princeton. edu week 1 1

Mechanics • COS 444 home page • Classes: - assigned reading: come ready to discuss - theory (ppt + chalk) - practice/discussion/news - experiments • Grading: - problem sets, programming assignments - class participation - term paper week 1 2

Background • • • week 1 Freshman calculus, integration by parts Basic probability, order statistics Statistics, significance tests Game theory, Nash equilibrium Java or UNIX tools or equivalent 3

Why study auctions? • Auctions are trade; trade makes civilization possible • Auctions are for selling things with uncertain value • Auctions are a microcosm of economics • Auctions are algorithms run on the internet • Auctions are a social entertainment week 1 4

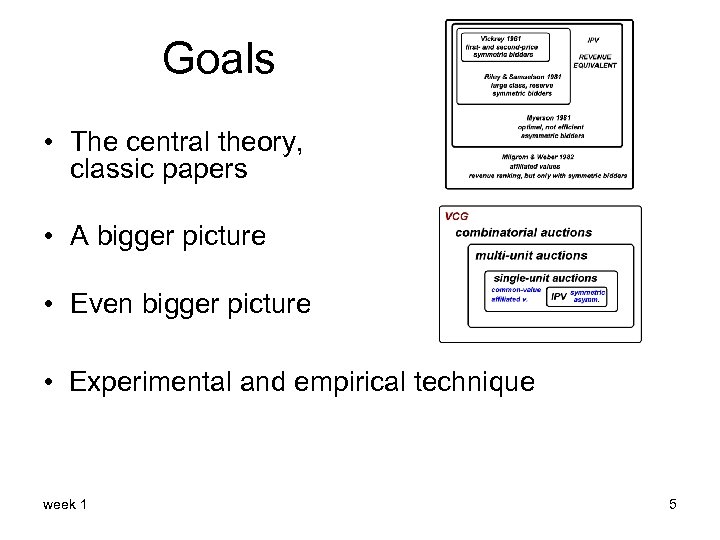Goals • The central theory, classic papers • A bigger picture • Even bigger picture • Experimental and empirical technique week 1 5

Cassady on the romance of auctions (1967) Who could forget, for example, riding up the Bosporus toward the Black Sea in a fishing vessel to inspect a fishing laboratory; visiting a Chinese cooperative and being the guest of honor at tea in the New Territories of the British crown colony of Hong Kong; watching the frenzied but quasi-organized bidding of would-be buyers in an Australian wool auction; observing the "upside-down" auctioning of fish in Tel Aviv and Haifa; watching the purchasing activities of several hundred screaming female fishmongers at the Lisbon auction market; viewing the fascinating "string selling" in the auctioning of furs in Leningrad; eating fish from the Seas of Galilee while seated on the shore of that historic body of water; … week 1 6

Cassady on the romance of auctions (1967). . . observing "whispered“ bidding in such far-flung places as Singapore and Venice; watching a "handshake" auction in a Pakistanian go-down in the midst of a herd of dozing camels; being present at the auctioning of an early Van Gogh in Amsterdam; observing the sale of flowers by electronic clock in Aalsmeer, Holland; listening to the chant of the auctioneer in a North Carolina tobacco auction; watching the landing of fish at 4 A. M. in the market on the north beach of Manila Bay by the use of amphibious landing boats; observing the bidding of Turkish merchants competing for fish in a market located on the Golden Horn; and answering questions about auctioning posed by a group of eager Japanese students at the University of Tokyo. week 1 7

Auctions: Methods of Study • • • week 1 Theory (1961 --) Empirical observation (recent on internet) Field experiments (recent on internet) Laboratory experiments (1980 --) Simulation (not much) f. MRI (? ) 8

History week 1 9

History week 1 10

History week 1 11

History week 1 12

History week 1 13

History week 1 14

History Route 6: Long John Nebel pitching hard week 1 15

Google Ad Auctions – Hal Varian week 1 16

Standard theoretical setup • • • One item, one seller n bidders Each knows her value vi (private value) Each wants to maximize her surplusi = vi – paymenti Values usually randomly assigned Values may be interdependent week 1 17

English auctions: variations • Outcry ( jump bidding allowed ) • Ascending price • Japanese button Truthful bidding is dominant in Japanese button auctions Is it dominant in outcry? Ascending price? week 1 18

Vickrey Auction: sealed-bid second-price William Vickrey, 1961 week 1 Vickrey wins Nobel Prize, 1996 19

Truthful bidding is dominant in Vickrey auctions Japanese button and Vickrey auctions are (weakly) strategically equivalent week 1 20

Dutch descending-price week 1 Aalsmeer flower market, Aalsmeer, Holland, 1960’s 21

week 1 22

Sealed-Bid First-Price • Highest bid wins • Winner pays her bid How to bid? That is, how to choose bidding function Notice: bidding truthfully is now pointless! week 1 23

Dutch and First-Price auctions are (strongly) strategically equivalent So we have two pairs, comprising the four most common auction forms week 1 24

Enter John Nash • Equilibrium translates question of human behavior to math • How much to shade? Nash wins Nobel Prize, 1994 week 1 25

Equilibrium • A strategy (bidding function) is a (symmetric) equilibrium if it is a best response to itself. • That is, if all others adopt the strategy, you can do no better than to adopt it also. Note: Cannot call this “optimal” week 1 26

Simple example: first-price • n=2 bidders • v 1 and v 2 uniformly distributed on [0, 1] • Find b (v 1 ) for bidder 1 that is best response to b (v 2 ) for bidder 2 in the sense that E [surplus ] = max Note: We need some probability theory for “uniformly distributed” and “E[ ]” week 1 27

Verifying a guess • Assume for now that v/ 2 is an equilibrium strategy • Bidder 2 bids v 2 / 2 ; Fix v 1. What is bidder 1’s best response b (v 1 ) ? E[surplus] = … the average is over the values of v 2 when 1 wins Bidders 1’s best choice of bid is b = v 1 / 2 … QED. week 1 28

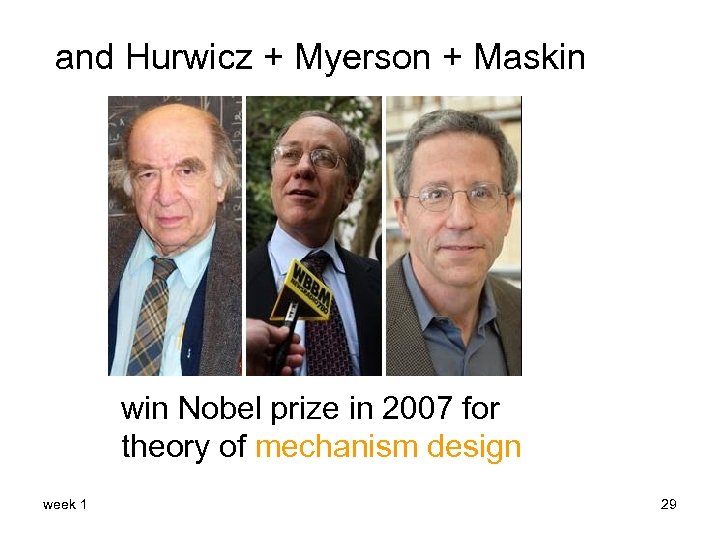and Hurwicz + Myerson + Maskin win Nobel prize in 2007 for theory of mechanism design week 1 29

New directions: Simulation Agent-Based Simulation of Dynamic Online Auctions, “ H. Mizuta and K. Steiglitz, Winter. Simulation Conference, Orlando, FL, Dec. 1013, 2000 week 1 30

New directions: Sociology M. Shohat and J. Musch “Online auctions as a research tool: A field experiment on ethnic discrimination” Swiss Journal of Psychology 62 (2), 2003, 139 -145 week 1 31

New directions: Category clustering Courtesy of Matt Sanders ’ 09 • Categories connected by mutual bidders • Darker lines mean higher probability that two categories will share bidders • Categories with higher totals near center • Color random • Only top 25% lines by weight are shown • Based on 278, 593 recorded auctions from bid histories of 18, 000 users week 1 32