COS 444 Internet Auctions Theory and Practice Spring

COS 444 Internet Auctions: Theory and Practice Spring 2010 Ken Steiglitz ken@cs. princeton. edu week 12 1

Bidder collusion • Of course, in general, bidders want to reduce competition, the seller wants to increase competition • We’ve seen examples on e. Bay of hypothetical implicit bidder collusion (Rasmusen 2006), and likely seller shill bidding • Collusive bidding may be easier in multi-item auctions • P. Cramton & J. A. Schwartz, “Collusive bidding in the FCC Spectrum Auctions, ” J. Regulatory Economics, 1999, describe (highly) probable collusion in simultaneous ascending price auctions for FCC licenses (analogous to English for multiple items). week 12 2

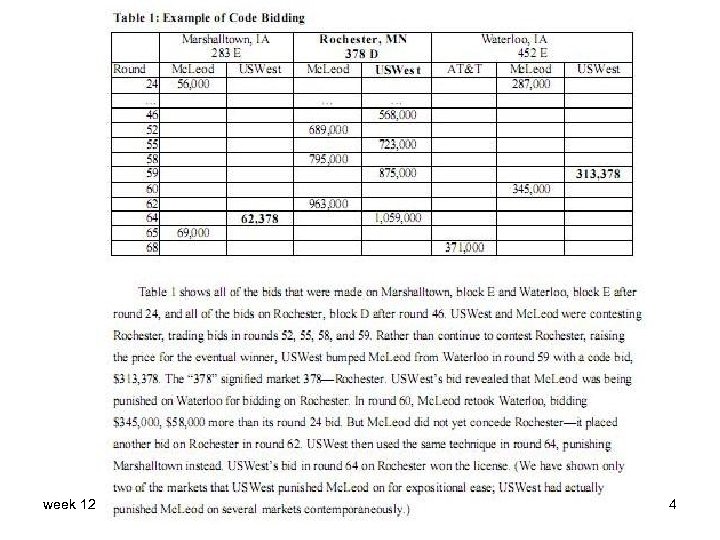
• Code bids: use the trailing digits of the bid (often multimillions of dollars) “to tell other bidders on which licenses to bid or not bid. … Oftentimes, a bidder (the sender) would use these code bids as retaliation against another bidder (the receiver) who was bidding on a license desired by the sender. The sender would raise the price on some market the receiver wanted, and use the trailing digits to tell the receiver on which license to cease bidding. ” Cramton & Schwartz 1999 week 12 3

week 12 4

• Here is their disclaimer: “Disclaimer: For this analysis, we show that several bidders apparently used signaling to coordinate on license allocations. This apparent signaling may be coincidental. The claims we make concerning a bidders signaling are based on circumstantial evidence, and though we may attach some meaning to help explain certain patterns of bidding, this meaning should be taken as our hypothesis only. We make no claims concerning the actual intent of the bidders. ” Cramton & Schwartz 1999 week 12 5

From a first-hand account of more explicit collusion week 12 6

“Marks & Co. were kings of the book ring. They were one of the five leading firms of antiquarian booksellers who never bid against each other in the auction rooms. One member of the ring would be allowed to buy a book for a nominal sum, say £ 100. As soon as the auction was over* the five conspirators would hurry to their nearest safe-house – usually a Lyons tea shop – and conduct a private auction. If one of them bought the book for £ 500, the £ 400 profit would be divided in cash amongst the other four†. This process was called a ‘knock-out’, and Frank Doel once blew an entire operation. Between Silk and Cyanide, Leo Marks, Harper Collins, London, 1998. week 12 * a post-auction knock-out †nota bene 7

“A famous heart specialist names Evan Bedford instructed him to bid up to £ 300 for an edition of Harvey’s De Motu Cordis, the earliest printed book on the circulation of the blood, which was coming up for auction at Hodgson’s. Too busy with his own Hartley Street salesroom to attend the auction himself, he telephoned Frank at home late at night demanding to know why the book had been sold to another dealer for £ 200 when he’d authorized Frank to bid three. Frank confided that it had been sold in the knock-out for £ 600. The irate physician immediately undertook to have the whole question of the book ring raised in the House of Commons, which caused cardiac arrest amongst its five participants. Between Silk and Cyanide, Leo Marks, Harper Collins, London, 1998. week 12 8

See Cassady 1967 for lots of details about real ring operations • He describes post-auction knockouts, “…the ring holds a private sale to liquidate [the goods] and divide them among ring members. ” (p. 180). Notice that the knockout is an example where the utility of a buyer includes some utility of the seller---since each prospective buyer has a stake in the seller’s revenue. • Organizing a ring is often a very complex operation. • Mentions that in sale of timber rights by U. S. gov’t. collusion is common; these sales have strong commonvalue features, similar to spectrum auctions. • Mentions Australian wool trade---the most complex buyer collusion known to Cassady. (p. 187) One buyer belonged to thirteen two-member and thirteen threemember rings. week 12 9

Bidder rings (Graham & Marshall 1987) Stylized facts: 1) They exist and are stable 2) They eliminate competition among ring members; yet ensure ring member with highest value is not undercut 3) Benefits shared by ring members 4) Have open membership 5) Auctioneer responds strategically 6) Try to hide their existence week 12 10

Graham & Marshall’s theoretical model: Secondprice pre- auction knockout (PAKT) • • IPV, risk neutral Value distributions F, common knowledge Identity of winner & price paid common knowledge Membership of ring known only to ring members week 12 11

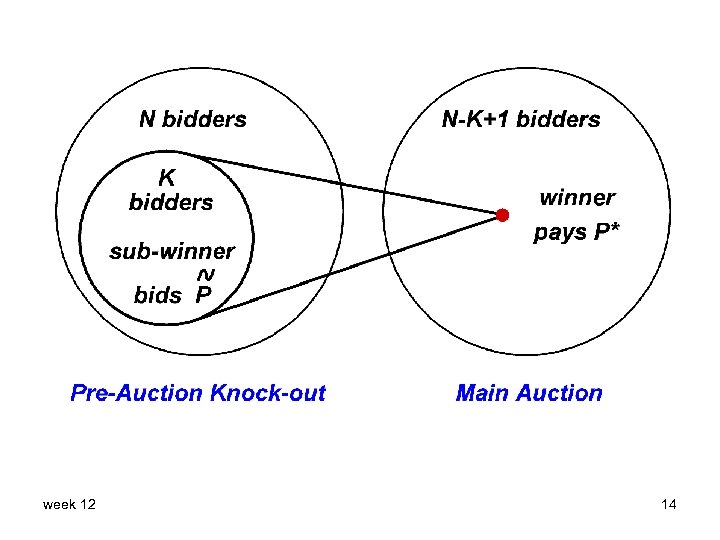
Pre-auction knock-out (PAKT): 1) Appoint ring center, who pays P to each ring member, P to be determined below 2) Each ring member submits a sealed bid to the ring center 3) Winner is advised to submit her winning bid at main auction; other ring members submit only meaningless bids 4) If the winner at the sub-auction (sub-winner) also wins main auction, she pays: week 12 12

If sub-winner wins main auction, she pays: • Main auctioneer P* = SP at main auction • Ring center δ = max{ P − P* , 0 }, where P = SP in PAKT Thus: If the sub-winner wins main auction, she pays in total the SP among all bids (which would have happened without the ring) and… the profit is passed along to the ring center week 12 13

week 12 14

The quantity δ is the amount “stolen” from the main auctioneer, the “booty” The ring center receives and distributes E[δ | sub-winner wins main auction] so his budget is balanced, in expectation Each ring member receives P = E[δ | sub-winner wins main auction]/K week 12 15

Bidder rings Graham and Marshall prove: 1) Truthful bidding in the PAKT, and following the recommendation of the ring center is a SBNE & weakly dominant strategy (incentive compatible) 2) Voluntary participation is advantageous (individually rational) 3) Efficient (buyer with highest value gets item) In fact, the whole thing is equivalent to a Vickrey auction week 12 16

Bidder rings Main auctioneer responds strategically by increasing reserves or shill-bidding Graham& Marshall also prove that 1) Optimal main reserve is an increasing function of ring size K 2) Expected surplus of ring member is a decreasing function of reserve prices 3) Expected surplus of ring member is an increasing function of ring size K … so best to be secretive week 12 17

Bilateral trading mechanisms [Myerson & Satterthwaite 83] An impossibility result: The following desirable characteristics of bilateral trade (not an auction): 1) efficient 2) incentive-compatible 3) individually rational cannot all be achieved simultaneously! week 12 18

Bilateral trading mechanisms The setup: • one seller, with private value v , distributed 1 with density f 1 > 0 on [a 1 , b 1 ] • one buyer, with private value v , 2 distributed with density f 2 > 0 on [a 2 , b 2 ] • risk neutral … Notice: not an auction in Riley & Samuelson’s class! week 12 19

Bilateral trading mechanisms • week 12 Outline of proof: We use a direct mechanism (p, x), where p (v 1 , v 2 ) = prob. of transfer to buyer x (v 1 , v 2 ) = expected payment to seller 20

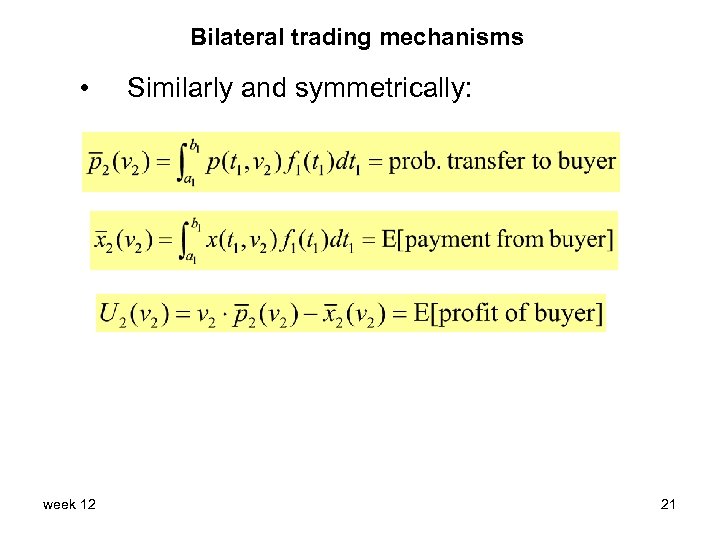Bilateral trading mechanisms • week 12 Similarly and symmetrically: 21

Bilateral trading mechanisms • Incentive-compatible means • Individually rational means • Ex post efficient means week 12 22

Bilateral trading mechanisms • Incentive-compatible means no incentive to lie about v’s • Individually rational means participation does not entail expected loss • Ex post efficient means object is sold iff buyer values it more highly week 12 23

Bilateral trading mechanisms Main result: If then no incentive-compatible individually rational trading mechanism can be (ex post) efficient. Furthermore, is the smallest lump-sum subsidy to achieve efficiency. week 12 24

Proof steps • Part 1: incentive-compatible and individually rational implies min. E[profit] of seller + min. E[profit] of buyer • Part 2: ex post efficient implies … contradiction! week 12 25

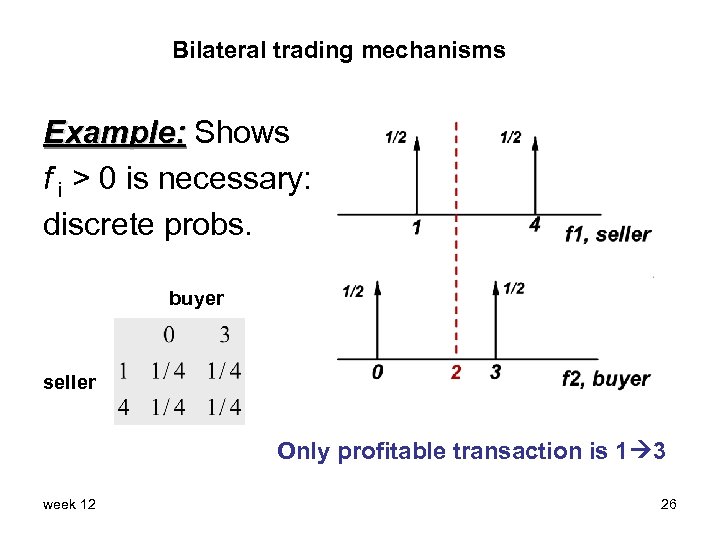Bilateral trading mechanisms Example: Shows f i > 0 is necessary: discrete probs. buyer seller Only profitable transaction is 1 3 week 12 26

Bilateral trading mechanisms Claim: “sell at price 2 if both are willing, else no trade” is incentive compatible, individually rational, and efficient. • • • week 12 Incentive compatible: truthful reporting is an equilibrium (check) Individually rational: E[profit] >0 Efficient: trade occurs only when v 1

Auctions vs. Negotiations [ Bulow & Klemperer 96 ] Simple example: IPV, uniform Case 1) Optimal auction = optimal mechanism with one buyer. Optimal entry value v* = 1/2; revenue = 1/4 Case 2) Two buyers, no reserve; revenue = 1/3 > 1/4 One more buyer is worth more than setting reserve optimally! week 12 28

Auctions vs. Negotiations Bulow & Klemperer 96 generalize to any F, any number of bidders… A no-reserve auction with n +1 bidders is more profitable than an optimal (IPV) auction (and hence optimal mechanism) with n bidders week 12 29

Auctions vs. Negotiations Revenue with optimal reserve, n bidders: Revenue with no reserve, n+1 bidders: week 12 30

Auctions vs. Negotiations Facts: Why? week 12 31

Auctions vs. Negotiations Facts: distribution fctn. of max. of n draws, integrate only where M ≥ 0 distribution fctn. of max. of n+1 draws expected revenue with only one buyer! week 12 32

Auctions vs. Negotiations Now compare revenue in a no-reserve auction with n+1 bidders, and an optimal auction with n bidders: □ week 12 33

“Rational frenzies and crashes, ” J. Bulow & P. Klemperer, J. Political Economy, 102, pp. 1 -23, 1994. • Asset markets are volatile! Common wisdom attributes to irrational behavior, market imperfections, market failure • This paper offers a model of a simple situation in which completely rational behavior leads to “frenzies” and “crashes” • Uses IPV auction theory and the RET in a dynamic setting • An elegant economic idealization makes the point week 12 34

The BK 94 game • K identical units for sale, one seller, K+L riskneutral potential buyers, each wanting to buy a single unit • IPV’s, drawn from F(v) on [0, vmax] • Buyer derives surplus (v – p) from a purchase at price p week 12 35

The simple motivating idea… WTP • Suppose you’re in a simple single-item Vickrey auction with IPV’s that are uniform on [0, 1], and you have value v. • You are made a take-it-or -leave-it offer at price p. Should you accept it? week 12 36

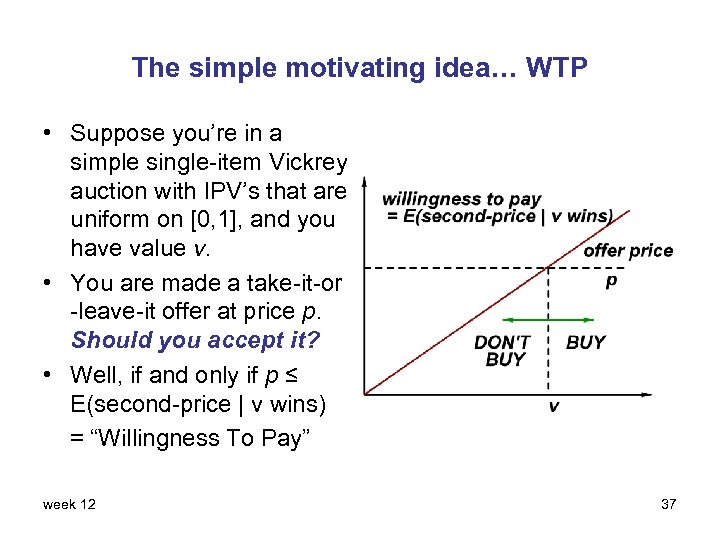The simple motivating idea… WTP • Suppose you’re in a simple single-item Vickrey auction with IPV’s that are uniform on [0, 1], and you have value v. • You are made a take-it-or -leave-it offer at price p. Should you accept it? • Well, if and only if p ≤ E(second-price | v wins) = “Willingness To Pay” week 12 37

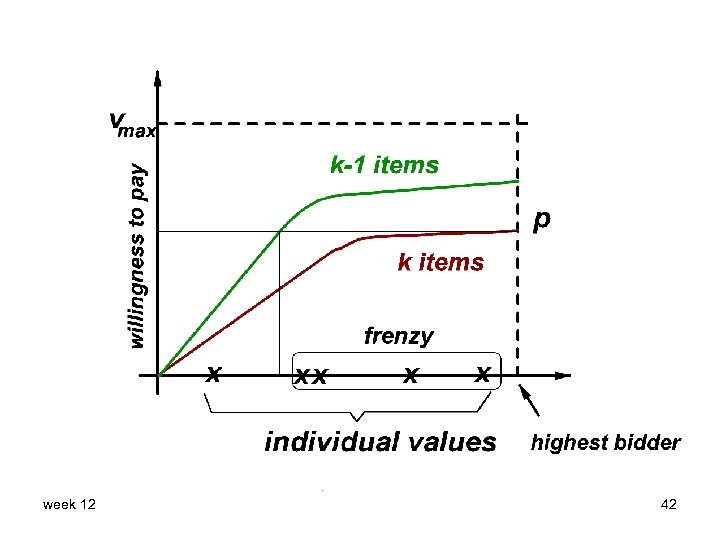
Dynamics of BK 94 game 1) 2) Seller begins offering units at max price vmax and lowers it until a purchase occurs, at price p (NEW SALE) When a purchase occurs, every buyer gets an invitation to purchase 1 unit at price p. Either: (a) (FRENZY) all goods are sold at p game ends (b) (FRENZY) not all goods are sold at p, no one is left willing to buy at that price then go to 1) and continue lowering price until another NEW SALE takes place (c) (EXCESS DEMAND) More buyers want to buy at price p than there are units remaining. Then if there are k+l bidders offering to buy the remaining k units, go to 1) and restart the game with these k+l bidders competing for the remaining k units. All previous sales remain valid. week 12 38

Solution to game • With k units and (k+l) bidders remaining: a symmetric equilibrium strategy is: offer to buy at price p if and only if p ≤ ω(v), where Note that this reduces to Vickrey with one item and one buyer week 12 39

• This follows from a straightforward generalization of the RET: any mechanism selling K identical items to the bidders with the K highest values in a unit-demand auction has in equilibrium the same expected payment conditional on winning, namely ω(v) (see B&K 94). • The interesting dynamics are a consequence of the shape of ω(v). When k goes down, ω(v) goes up, and this changes the next threshold drastically and a bunch of buyers may jump in all at once! week 12 40

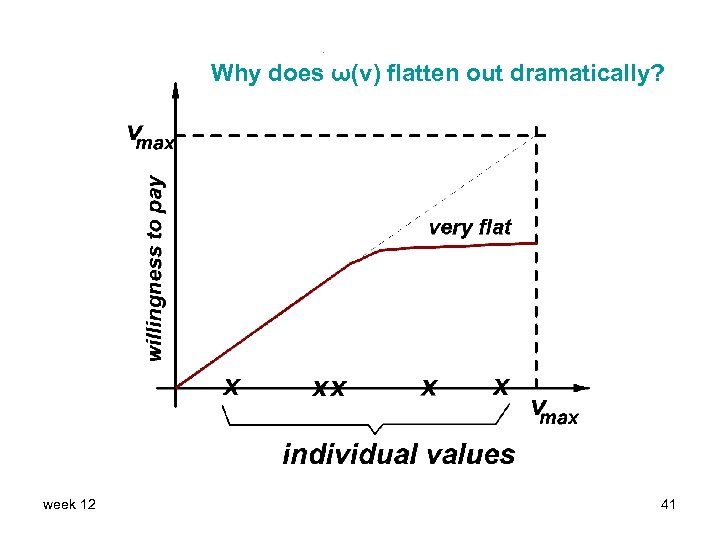Why does ω(v) flatten out dramatically? week 12 41

week 12 42

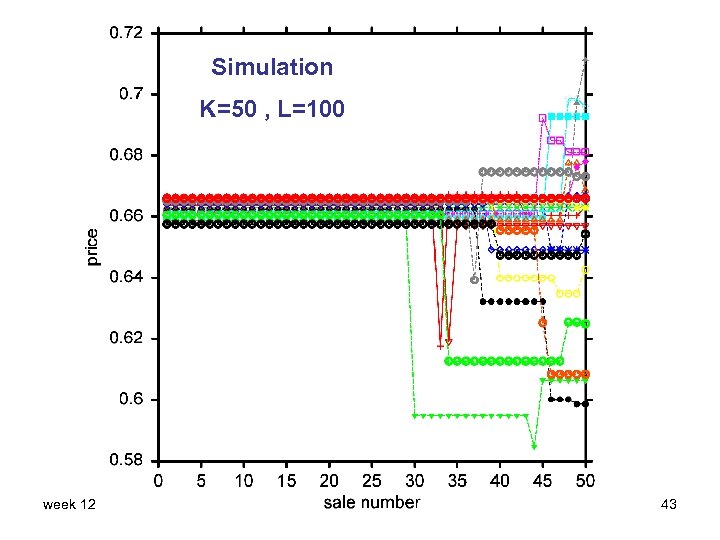Simulation K=50 , L=100 week 12 43

Term papers due 5 pm Tuesday May 11 (Dean’s Date) Email me for office hours re term papers It’s been fun! Neshmet Bark of Osiris, on a bronze drachm of M. Aurelius, Alexandria, Egypt. E. 2160, 174/5 AD. week 12 44