Correctness Proofs and Counter-model Generation with Authentication-Protocol Logic

Correctness Proofs and Counter-model Generation with Authentication-Protocol Logic Koji Hasebe Mitsuhiro Okada Department of Philosophy, Keio University

Background n Security protocols: n n n Communication over insecure network Cryptography used for authentication, secrecy, etc. Formal analysis of security protocols: n n Assume perfect encryption Assume existence of intruder who may. . . • • See all exchanged messages Delete, alter, inject and redirect messages Initiate new communications Reuse messages from past sessions

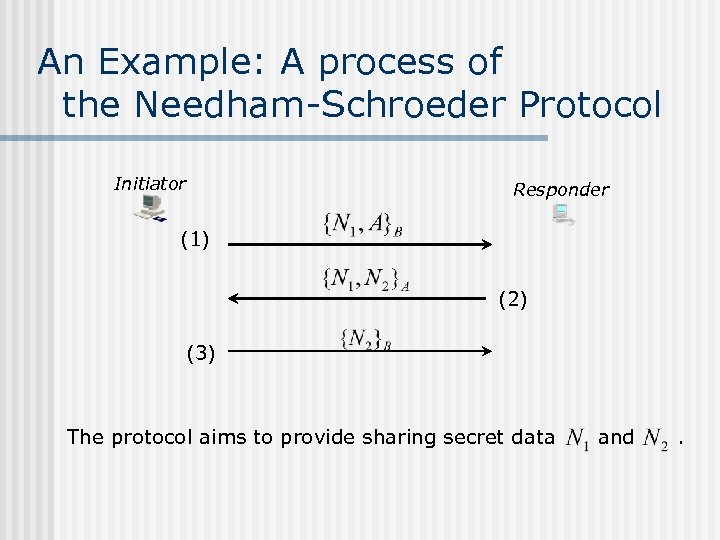An Example: A process of the Needham-Schroeder Protocol Initiator Responder (1) (2) (3) The protocol aims to provide sharing secret data and .

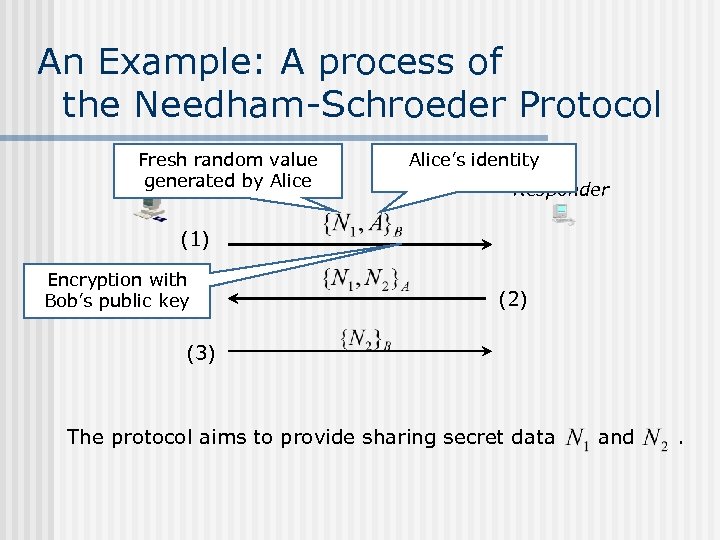An Example: A process of the Needham-Schroeder Protocol Fresh random value generated by Alice Initiator Alice’s identity Responder (1) Encryption with Bob’s public key (2) (3) The protocol aims to provide sharing secret data and .

The agreement property Initiator Responder sends receives Instantiation (Here are constants, and substitution Instantiation. )

The agreement property Initiator Responder sends receives Initiator’s role (Here Responder’s role are variables. )

The agreement property Initiator Responder sends receives Definition: has agreement property w. r. t. For any substitution and for any process , if contains execution of responder’s role and an initiator’s execution according to , then contains .

An attack on the NS protocol [Lowe, 1996] Alice Intruder Bob (1) (1’) (2) (3’) n n From Bob's view, Bob believes that Alice communicates with Bob, but actually Alice communicates with Intruder. This attack has nothing to do with cryptography.

Proving vs Model Checking (Two approaches for protocol verifications) n Inference rule-based deductive approaches: BAN logics (Burrows-Abadi-Needham, 1989) n Protocol logics (or Compositional logics) etc. n n Trace-based semantic approaches: n MSR (Cervesato-Durgin-Lincoln-Mitchell-Scedrov, 1999) Strand space (Thayer Fabrega-Herzog-Guttman, 1998) etc. n

Protocol Logics Durgin-Mitchell-Pavlovic (2001), Datta-Derek-Mitchell-Pavlovic (2003 -), Cervesato-Meadows-Pavlovic (2004 -), Hasebe-Okada (2004) Inference systems to prove protocols correct n Primitive actions (“sending”, “receiving”, “generating”, etc. ) are described as predicate symbols n Some properties about nonces and keys are formalized as non-logical axioms n Prove correctness in the logical system

Proving vs Model Checking

Proving = Model Checking By completeness proof based on the proof-search (i. e. , bottom-up proof construction) method

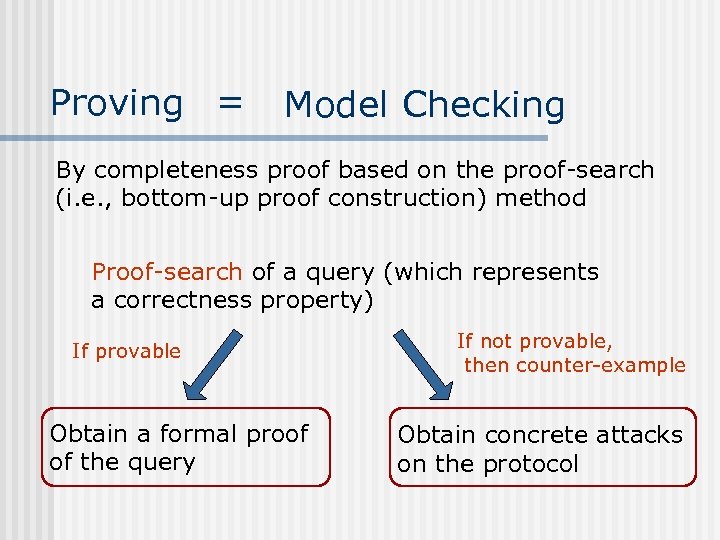Proving = Model Checking By completeness proof based on the proof-search (i. e. , bottom-up proof construction) method Proof-search of a query (which represents a correctness property) If provable Obtain a formal proof of the query If not provable, then counter-example Obtain concrete attacks on the protocol

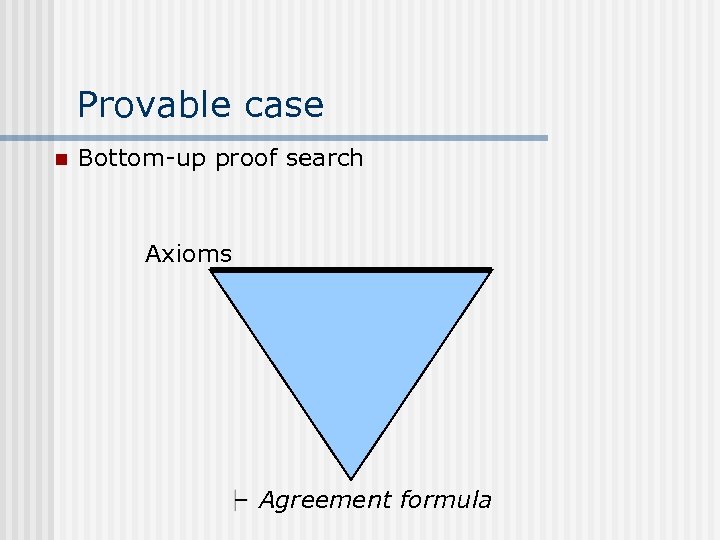Provable case n Bottom-up proof search Axioms Agreement formula

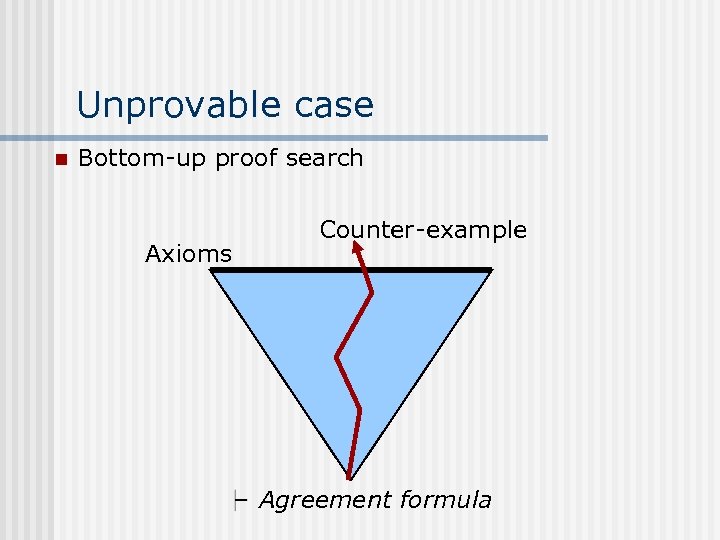Unprovable case n Bottom-up proof search Axioms Counter-example Agreement formula

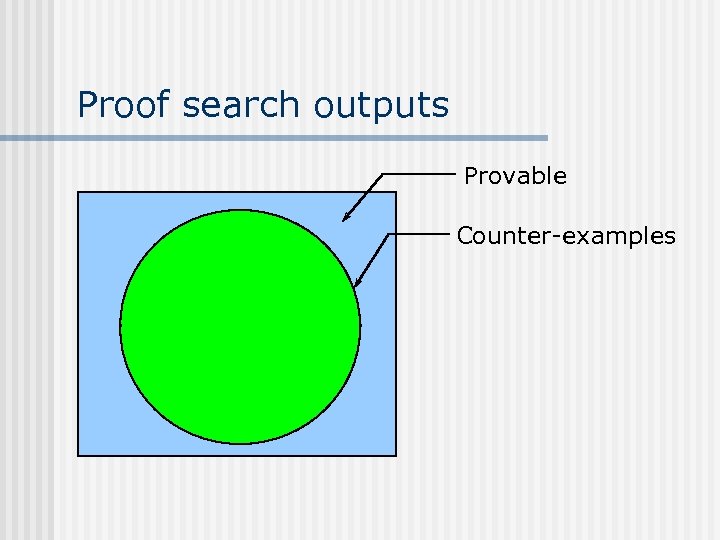Proof search outputs Provable Counter-examples

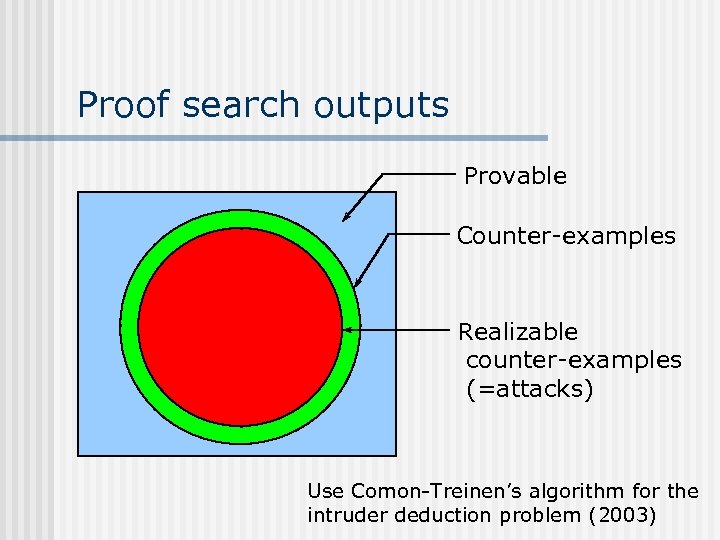Proof search outputs Provable Counter-examples Realizable counter-examples (=attacks) Use Comon-Treinen’s algorithm for the intruder deduction problem (2003)

Main results for agreement property with a bounded number of sessions 1. Basic part of Protocol Logic is describable in first-order predicate logic. 2. First-order proof search-based completeness proof is applicable to our Basic Protocol Logic, hence, usable for proving correctness and detecting attacks at once. 3. Provability of correctness property is decidable (by finite domain property).

1. 2. 3. Basic Protocol Logic (or BPL, for short) Proof search-based completeness proof Example of our proof construction / counter-example generation

Language of Basic Protocol Logic (1) n n Sorts: name, nonce, message, (key) Terms: n Atomic terms: • • • : atomic terms of sort (principal) name : atomic terms of sort nonce : variables of sort message • All atomic terms of sort name and nonce are terms of sort message. n Compound terms of sort message:

Language of Basic Protocol Logic (2) Formulas: n Atomic formulas: Trace formula: a sequence of primitive actions (denoted by , or ) (Here we use sends, receives, generates as primitive actions. ) n e. g. (P generates n n before P sends before Q receives Equality and subterm relations ( Compound formulas: Made by first-order logical connectives ) . )

Logical Axioms of BPL n n Base: Axioms of frist-order predicate logic with equality Rules for trace formulas: n (for ) n (where are the list of order-preserving merges of and example: (the list of order-preserving merges) n Axioms of universal sentences over terms (known as decidable [Venkataraman 87]): if is axiom is valid in free term algebra. )

An example of the non-logical axioms: Nonce Verification axiom (Cf. Authentication-tests based Strand space) does not include (i. e. , is not a forwarded message). is the only message sent by P which includes Intuitive meaning: .

An example of the non-logical axioms: Nonce Verification axiom (Cf. Authentication tests based strand space) does not include (i. e. , is not a forwarded message). is the only message sent by P which includes . Intuitive meaning: decrypt send back

An example of the non-logical axioms: Nonce Verification axiom (Cf. Authentication tests based strand space) does not include (i. e. , is not a forwarded message). is the only message sent by P which includes First order formalization: .

An example of Honesty (The Needham-Schroeder protocol) n A’s honesty: (( A performs no action ) ( A performs and A does not perform any other actions)) A’s run (A performs no action) (0) (1) (2)

Formalization of Honesty (The Needham-Schroeder protocol) n A’s honesty (described in BPL)

Main Results on BPL n Complete for a certain formal trace semantics. n Decidable for Provability of the query (which represents an agreement property). n Applicable to counter-example generations (i. e. , flaw detections)

Formal Trace-Based Semantics A formal trace model: n : name domain n : nonce domain n : free term algebra domain on n : a sequence of primitive actions n : valuation and along with , , n is extended to interpretation: n n Truth conditions: n n n etc.

Completeness Theorem For any query (which represents an agreement property), the formula is provable in BPL iff it is true for any model

Completeness Proof (1) Proof-Search Tree Construction n n Proof-search (i. e. , bottom-up proof construction) is based on the sequent calculus of first-order predicate logic Proof-search tree is constructed in Rounds: (Each round decomposes the outermost logical symbols. ) n Round 0 : put the query at the bottom of the tree n Round i : apply the rules for logical connectives (then go to Round i+1 unless the current topmost sequent is closed, i. e. , matches an axiom. )

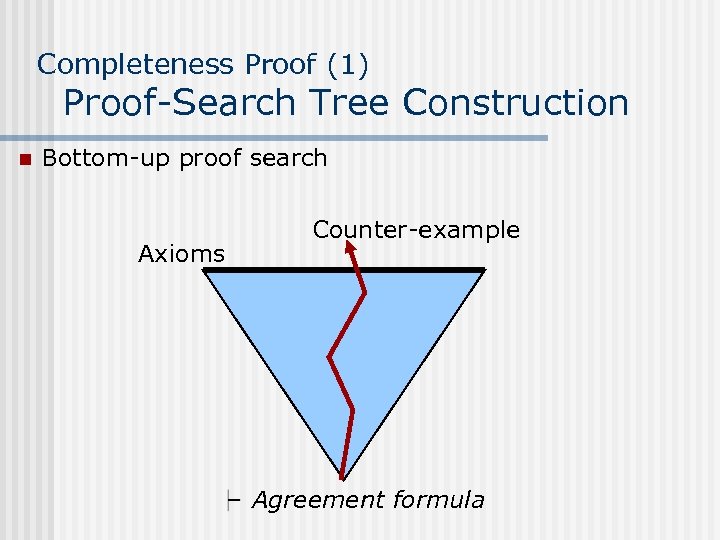Completeness Proof (1) Proof-Search Tree Construction n Bottom-up proof search Axioms Counter-example Agreement formula

Completeness Proof (2) Main Lemma For any given query (which represents an agreement property), if its proof-search tree includes a branch which is not closed at the end of Round 3, then there exists a countermodel for the query.

Completeness Proof (3) Construction of Counter-Models n A model which is obtained from a topmost nonclosed sequent at the end of Round 3 (say, ) is as follows: 1. Take the set of literals from problem of these literals. and , and solve the satisfaction 2. Decompose each literal which consists of compound terms. 3. (e. g. , and ) 3. Take representatives as n and . : n , . n (where is the representative of the equivalence class of ) . n Interpretations for compound terms and formulas are defined by inductions. n

Completeness Proof (4) Essential Idea Let T be the set of terms in Round 3. For any variable (say, which appears above Round 3, an equation m=t with some t always appears in the left side. ) T Search domain does not increase above Round 3. (closed) left ( : new variable) (Axiom of Query: , formula) (in Honesty) ,

Decidability From Main Lemma and Soundness: If a query is provable in BPL, then the proof-construction procedure terminates by Round 3.

Counter-Example Generations (1) Realizable Traces n We cannot directly consider counter-models to be an attack on the protocol in question, because some of them cannot be realizable. (An example of the unrealizable trace) Use Comon-Treinen’s algorithm for the intruder deduction problem (2003).

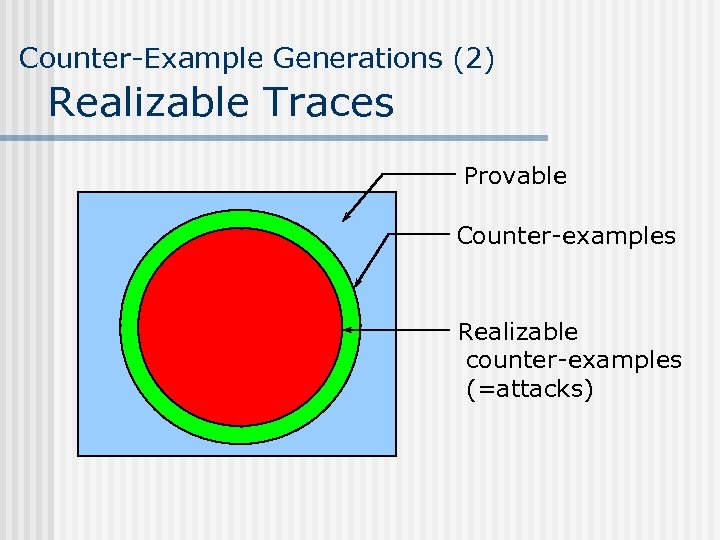Counter-Example Generations (2) Realizable Traces Provable Counter-examples Realizable counter-examples (=attacks)

Proposition For any given query, we can determine whethere exists a realizable counterexample (i. e. , a concrete attack on the protocol in question) whenever we set any upper-bound on the number of sessions.

Example: Proof construction and counter-example generation of the Needham-Schroeder The NS protocol

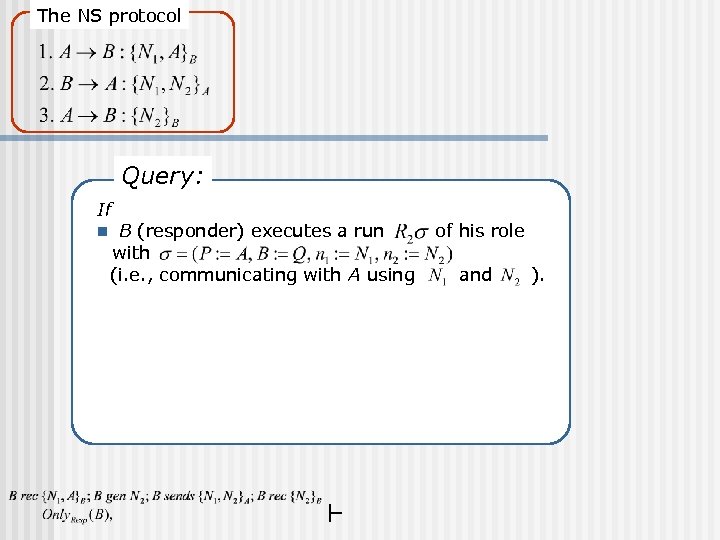The NS protocol Query: If n B (responder) executes a run with (i. e. , communicating with A using of his role and ).

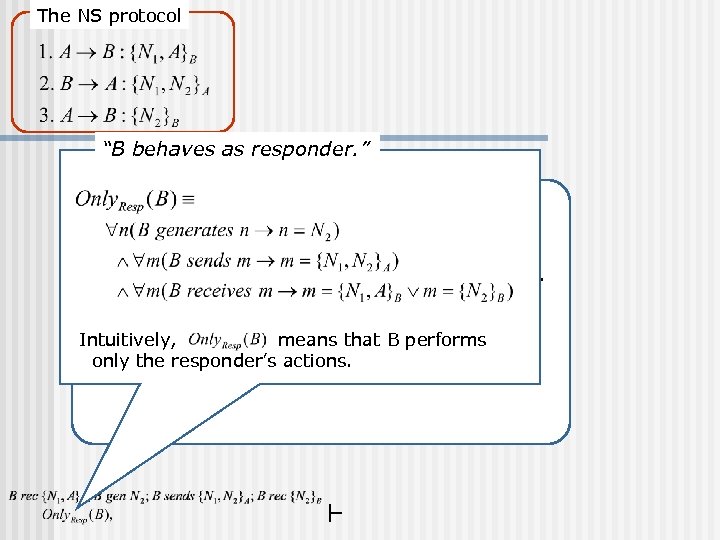The NS protocol “B behaves as responder. ” Query: If n B (responder) executes a run with (i. e. , communicating with A using of his role and Intuitively, means that B performs only the responder’s actions. ).

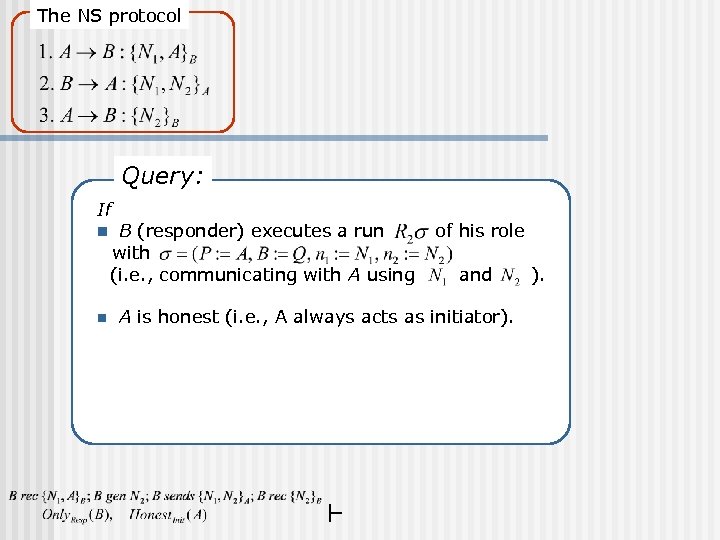The NS protocol Query: If n n B (responder) executes a run with (i. e. , communicating with A using of his role and A is honest (i. e. , A always acts as initiator).

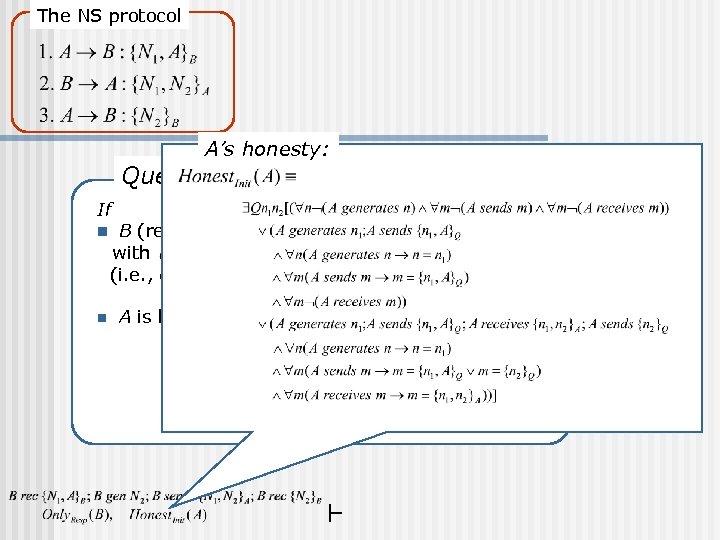The NS protocol Query: If n n A’s honesty: B (responder) executes a run with (i. e. , communicating with A using of his role and A is honest (i. e. , A always acts as initiator).

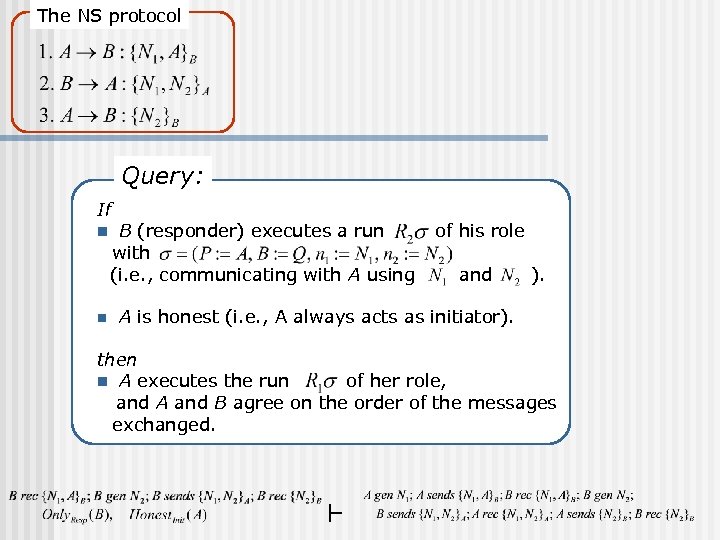The NS protocol Query: If n n B (responder) executes a run with (i. e. , communicating with A using of his role and ). A is honest (i. e. , A always acts as initiator). then n A executes the run of her role, and A and B agree on the order of the messages exchanged.

The NS protocol

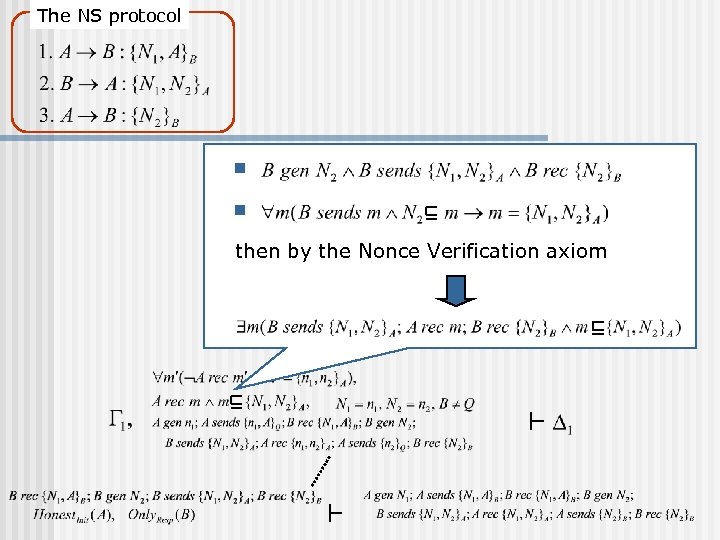The NS protocol n n then by the Nonce Verification axiom

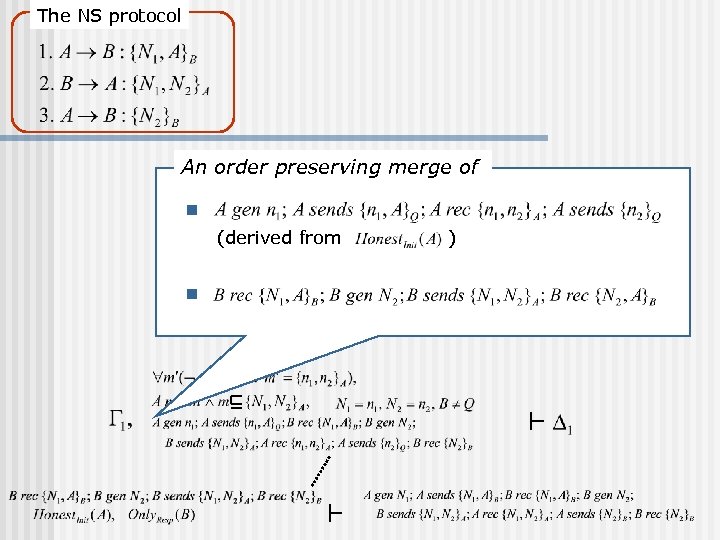The NS protocol An order preserving merge of n (derived from n )

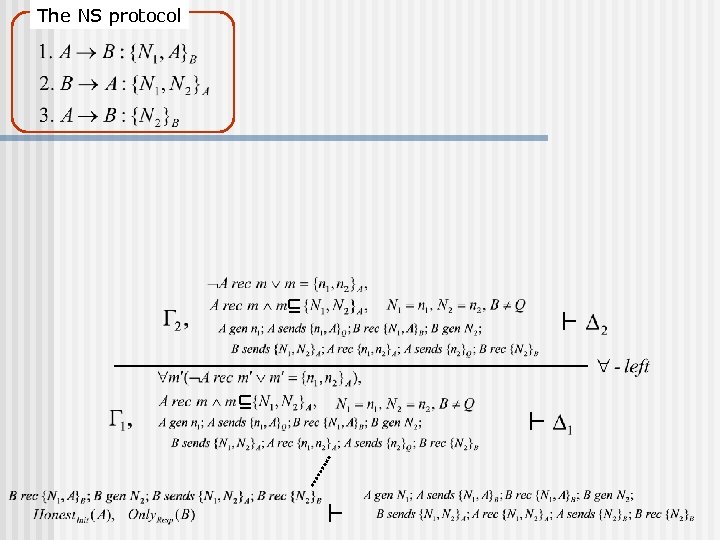The NS protocol

The NS protocol Obtained by instantiation for where is the list of terms such that n The length is less than or equal to the maximal length of terms appearing in the query. n Each is constructed by atomic terms appearing in the lower sequent.

The NS protocol

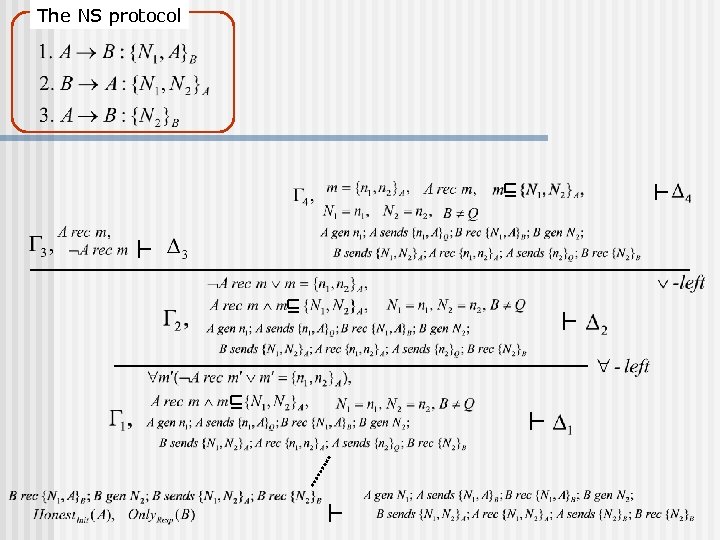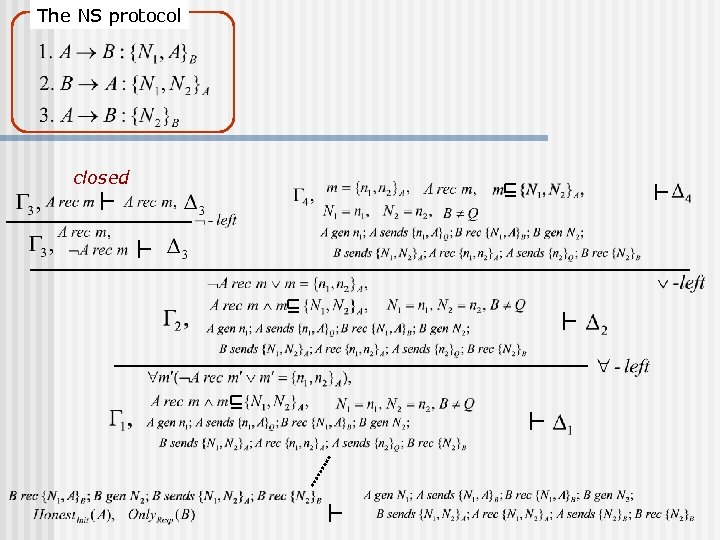The NS protocol closed

The NS protocol This branch is not closed is not valid in the free term algebra. is not axiom.

The NS protocol Countermodel (with closed )

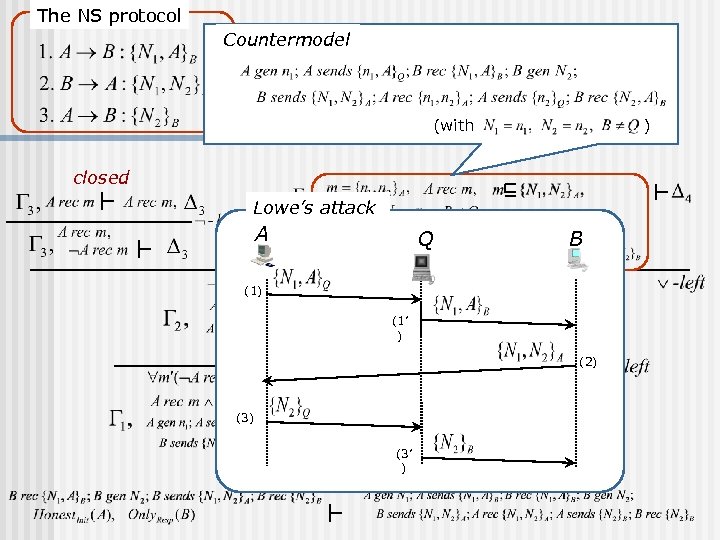The NS protocol Countermodel (with ) closed Lowe’s attack A Q B (1) (1’ ) (2) (3’ )

The NSL protocol Lowe’s modification of the NS protocol:

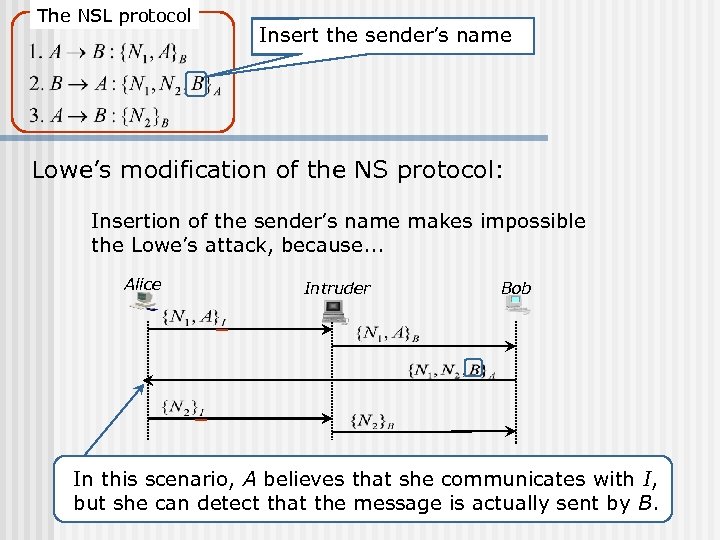The NSL protocol Insert the sender’s name Lowe’s modification of the NS protocol: Insertion of the sender’s name makes impossible the Lowe’s attack, because. . . Alice Intruder Bob In this scenario, A believes that she communicates with I, but she can detect that the message is actually sent by B.

The NSL protocol closed

The NSL protocol This branch is closed

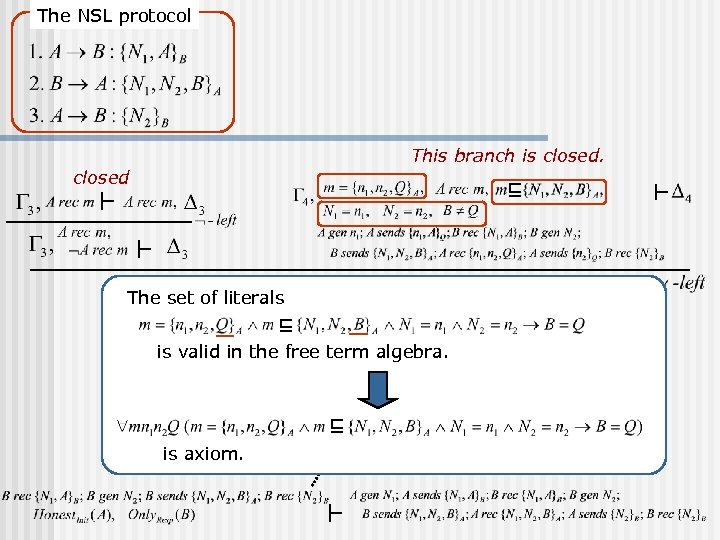The NSL protocol This branch is closed The set of literals is valid in the free term algebra. is axiom.

Realizable counter-examples of the NS protocol (1) n In the proof-search tree, there are some open branches, and each topmost sequent is: n Left side includes an order-preserving merge of the following trace formulas u u (where ) n are satisfied.

Realizable counter-examples of the NS protocol (2) n Counter-model n where an order-preserving merge of the following formulas n u u

Conclusions and Future Work n n n Gave an inference system for proving protocols correct based on first-order predicate logic Showed completeness and decidability Presented how to construct proofs / generate counter-examples Implementation for automation Compositionality issue for automated protocol design