ae593213c30de8edbae62a2139e97475.ppt
- Количество слайдов: 50
 Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 1
Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 1
 Try these problems l Ch 6 u. Problem 12 u. Problems 14 -16 (see p 157) l Ch 7 u. Problem 1 u. Problem 5 Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 2
Try these problems l Ch 6 u. Problem 12 u. Problems 14 -16 (see p 157) l Ch 7 u. Problem 1 u. Problem 5 Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 2

 New York University/ING Barings Portfolio Diversification and the Capital Asset Pricing Model Prof. Ian Giddy New York University
New York University/ING Barings Portfolio Diversification and the Capital Asset Pricing Model Prof. Ian Giddy New York University
 Equity Risk and Return: Summary Investors diversify, because you get a better return for a given risk. l There is a fully-diversified “market portfolio” that we should all choose l The risk of an individual asset can be measured by how much risk it adds to the “market portfolio. ” l Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 5
Equity Risk and Return: Summary Investors diversify, because you get a better return for a given risk. l There is a fully-diversified “market portfolio” that we should all choose l The risk of an individual asset can be measured by how much risk it adds to the “market portfolio. ” l Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 5
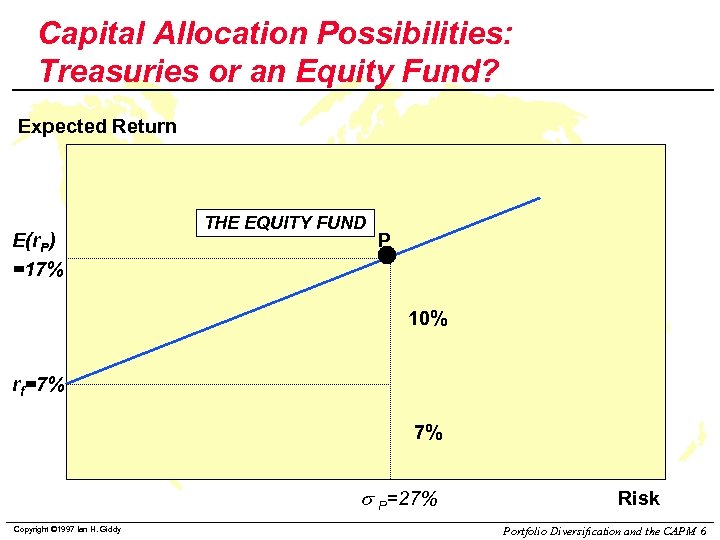 Capital Allocation Possibilities: Treasuries or an Equity Fund? Expected Return E(r. P) =17% THE EQUITY FUND P 10% rf=7% 7% s P=27% Copyright © 1997 Ian H. Giddy Risk Portfolio Diversification and the CAPM 6
Capital Allocation Possibilities: Treasuries or an Equity Fund? Expected Return E(r. P) =17% THE EQUITY FUND P 10% rf=7% 7% s P=27% Copyright © 1997 Ian H. Giddy Risk Portfolio Diversification and the CAPM 6
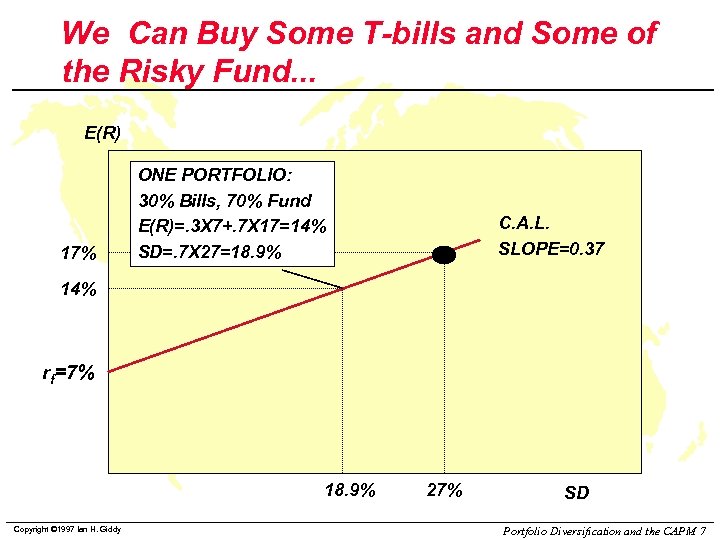 We Can Buy Some T-bills and Some of the Risky Fund. . . E(R) 17% ONE PORTFOLIO: 30% Bills, 70% Fund E(R)=. 3 X 7+. 7 X 17=14% SD=. 7 X 27=18. 9% C. A. L. SLOPE=0. 37 14% rf=7% 18. 9% Copyright © 1997 Ian H. Giddy 27% SD Portfolio Diversification and the CAPM 7
We Can Buy Some T-bills and Some of the Risky Fund. . . E(R) 17% ONE PORTFOLIO: 30% Bills, 70% Fund E(R)=. 3 X 7+. 7 X 17=14% SD=. 7 X 27=18. 9% C. A. L. SLOPE=0. 37 14% rf=7% 18. 9% Copyright © 1997 Ian H. Giddy 27% SD Portfolio Diversification and the CAPM 7
 . . . Or Buy Two Risky Assets E(r) A B Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 8
. . . Or Buy Two Risky Assets E(r) A B Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 8
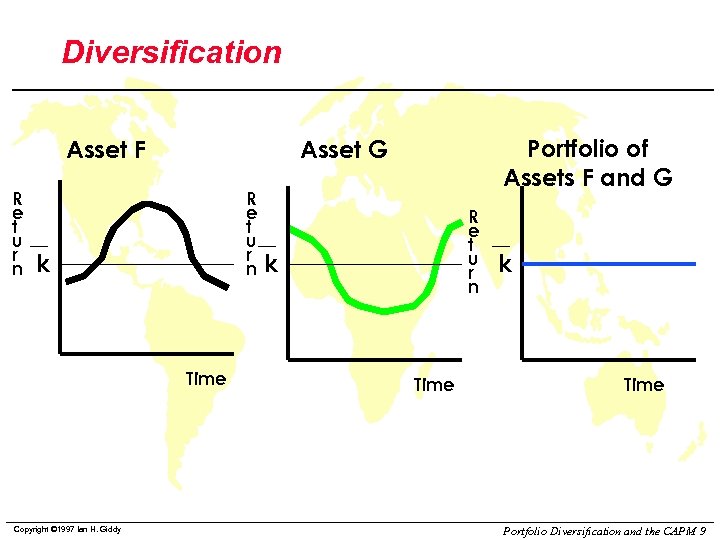 Diversification Asset F R e t u r n k Time Copyright © 1997 Ian H. Giddy Portfolio of Assets F and G Asset G R e t u r n k Time Portfolio Diversification and the CAPM 9
Diversification Asset F R e t u r n k Time Copyright © 1997 Ian H. Giddy Portfolio of Assets F and G Asset G R e t u r n k Time Portfolio Diversification and the CAPM 9
 Portfolio Return. . . To compute the return of a portfolio: use the weighted average of the returns of all assets in the portfolio, with the weight given each asset calculated as (value of asset)/(value of portfolio). The portfolio return E(Rp) is: E(Rp) = (w 1 k 1)+(w 2 k 2)+. . . (wnkn) = S wj kj where wj = weight of asset j, kj = return on asset j Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 10
Portfolio Return. . . To compute the return of a portfolio: use the weighted average of the returns of all assets in the portfolio, with the weight given each asset calculated as (value of asset)/(value of portfolio). The portfolio return E(Rp) is: E(Rp) = (w 1 k 1)+(w 2 k 2)+. . . (wnkn) = S wj kj where wj = weight of asset j, kj = return on asset j Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 10
 . . . and Risk (Standard Deviation) Portfolio return is the weighted average of all assets’ returns, l But portfolio standard deviation is normally less than the weighted average of all assets’ standard deviations! l The reason: asset returns are imperfectly correlated. l Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 11
. . . and Risk (Standard Deviation) Portfolio return is the weighted average of all assets’ returns, l But portfolio standard deviation is normally less than the weighted average of all assets’ standard deviations! l The reason: asset returns are imperfectly correlated. l Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 11
 Measuring Portfolio Risk The variance of a 2 -asset portfolio is: where w. A and w. B are the weights of A and B in the portfolio. Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 12
Measuring Portfolio Risk The variance of a 2 -asset portfolio is: where w. A and w. B are the weights of A and B in the portfolio. Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 12
 Return and Risk, Generalized Portfolio return: where wi are the weights of each asset in the portfolio. (Expected return is simply the weighted sum of the individual asset returns. ) Portfolio variance: When i = j, the term wiwj. Fi. Fj. Dij becomes wi 2 Fi 2. Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 13
Return and Risk, Generalized Portfolio return: where wi are the weights of each asset in the portfolio. (Expected return is simply the weighted sum of the individual asset returns. ) Portfolio variance: When i = j, the term wiwj. Fi. Fj. Dij becomes wi 2 Fi 2. Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 13
 Covariance and Correlation The correlation coefficient scales the covariance to a value between -1 and +1: Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 15
Covariance and Correlation The correlation coefficient scales the covariance to a value between -1 and +1: Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 15
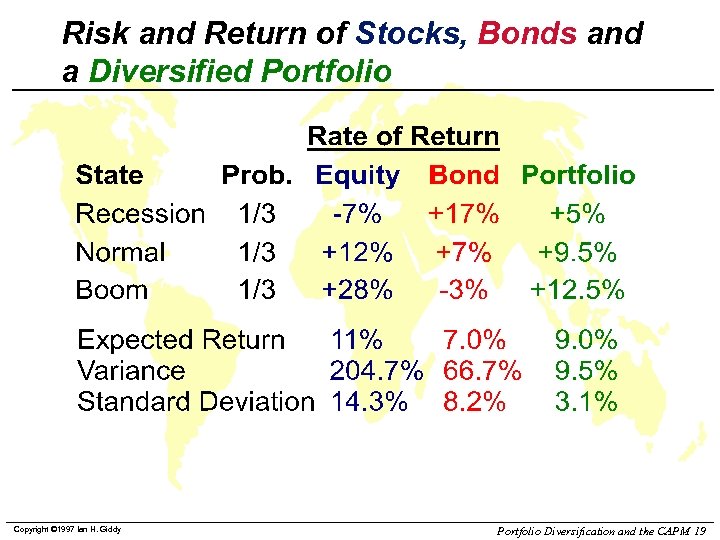 Risk and Return of Stocks, Bonds and a Diversified Portfolio Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 19
Risk and Return of Stocks, Bonds and a Diversified Portfolio Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 19
 The Correlation Between Stock and Bond Returns l Covariance = 0. 3333(-7 -11)(17 -7) + 0. 3333(12 -11)(7 -7) +0. 3333(28 -11)(-3 -7) = -116. 67 l Correlation = -116. 66 / 14. 3(8. 2) = -0. 99 Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 20
The Correlation Between Stock and Bond Returns l Covariance = 0. 3333(-7 -11)(17 -7) + 0. 3333(12 -11)(7 -7) +0. 3333(28 -11)(-3 -7) = -116. 67 l Correlation = -116. 66 / 14. 3(8. 2) = -0. 99 Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 20
 Portfolio Return and Standard Deviation Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 21
Portfolio Return and Standard Deviation Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 21
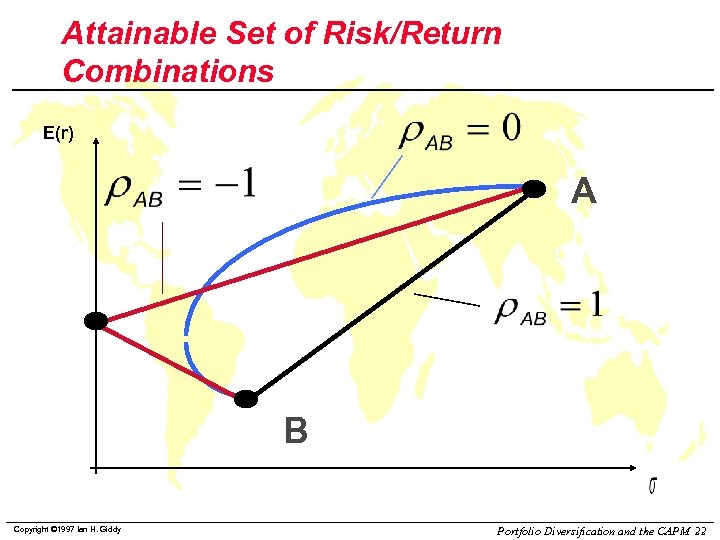 Attainable Set of Risk/Return Combinations E(r) A B Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 22
Attainable Set of Risk/Return Combinations E(r) A B Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 22
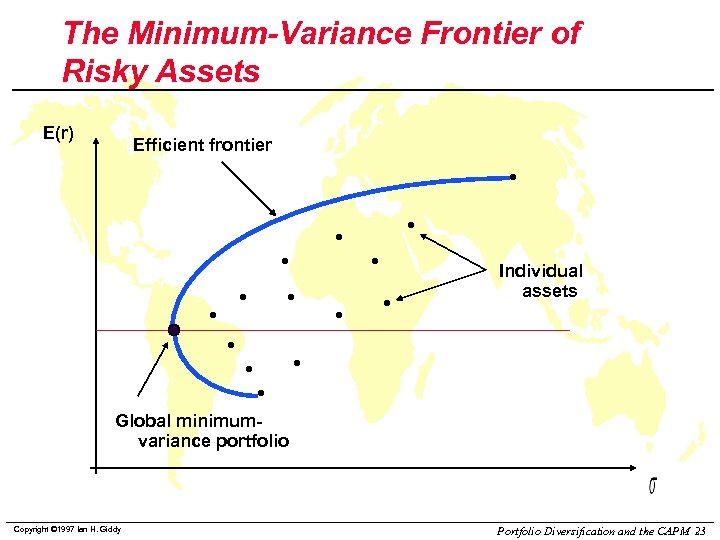 The Minimum-Variance Frontier of Risky Assets E(r) Efficient frontier Individual assets Global minimumvariance portfolio Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 23
The Minimum-Variance Frontier of Risky Assets E(r) Efficient frontier Individual assets Global minimumvariance portfolio Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 23
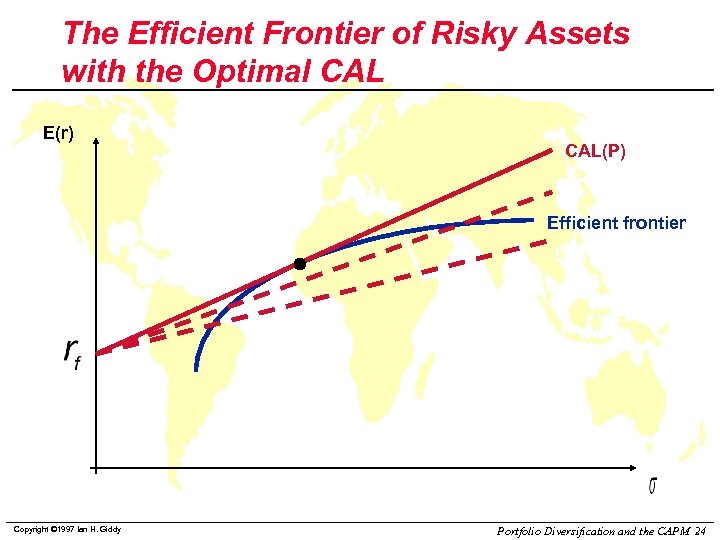 The Efficient Frontier of Risky Assets with the Optimal CAL E(r) CAL(P) Efficient frontier Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 24
The Efficient Frontier of Risky Assets with the Optimal CAL E(r) CAL(P) Efficient frontier Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 24
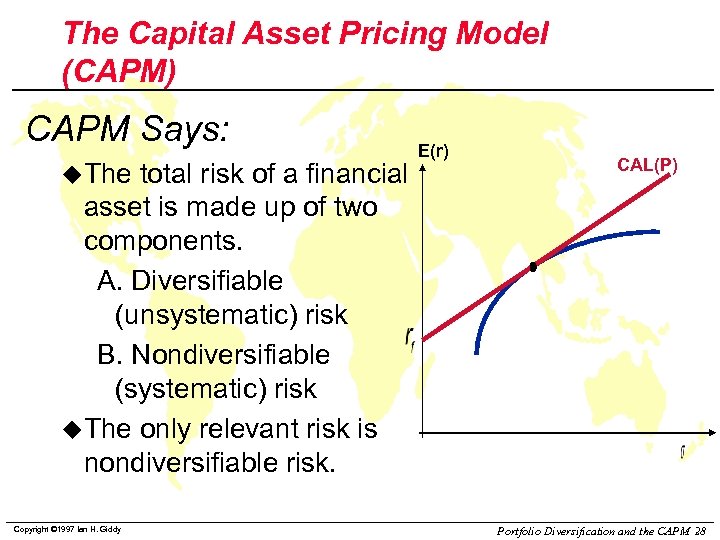 The Capital Asset Pricing Model (CAPM) CAPM Says: u. The total risk of a financial asset is made up of two components. A. Diversifiable (unsystematic) risk B. Nondiversifiable (systematic) risk u. The only relevant risk is nondiversifiable risk. Copyright © 1997 Ian H. Giddy E(r) CAL(P) Portfolio Diversification and the CAPM 28
The Capital Asset Pricing Model (CAPM) CAPM Says: u. The total risk of a financial asset is made up of two components. A. Diversifiable (unsystematic) risk B. Nondiversifiable (systematic) risk u. The only relevant risk is nondiversifiable risk. Copyright © 1997 Ian H. Giddy E(r) CAL(P) Portfolio Diversification and the CAPM 28
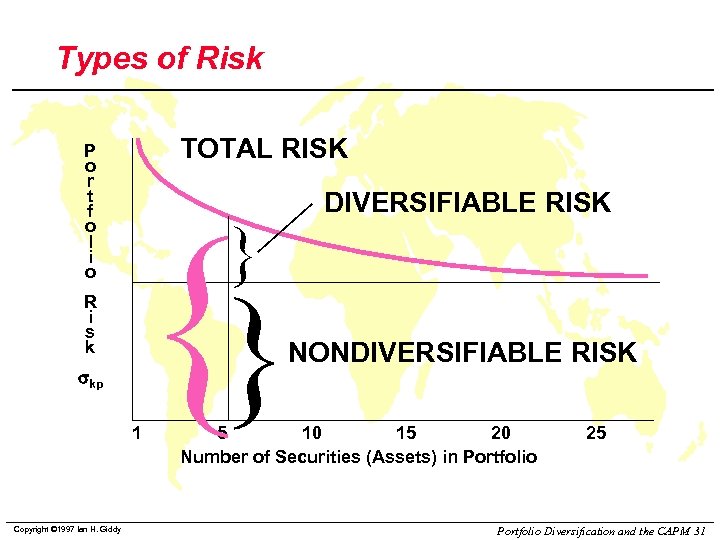 Types of Risk TOTAL RISK P o r t f o l i o R i s k skp 1 Copyright © 1997 Ian H. Giddy {} } DIVERSIFIABLE RISK NONDIVERSIFIABLE RISK 5 10 15 20 Number of Securities (Assets) in Portfolio 25 Portfolio Diversification and the CAPM 31
Types of Risk TOTAL RISK P o r t f o l i o R i s k skp 1 Copyright © 1997 Ian H. Giddy {} } DIVERSIFIABLE RISK NONDIVERSIFIABLE RISK 5 10 15 20 Number of Securities (Assets) in Portfolio 25 Portfolio Diversification and the CAPM 31
 The Model: CAPM The CAPM (Capital Asset Pricing Model) links together nondiversifiable risk and return for all assets: A. Beta Coefficient (b) is a relative measure of nondiversifiable risk; an index of the change of an asset's return in response to a change in the market return B. Market Return (km) is the return on the market portfolio of all traded securities Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 32
The Model: CAPM The CAPM (Capital Asset Pricing Model) links together nondiversifiable risk and return for all assets: A. Beta Coefficient (b) is a relative measure of nondiversifiable risk; an index of the change of an asset's return in response to a change in the market return B. Market Return (km) is the return on the market portfolio of all traded securities Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 32
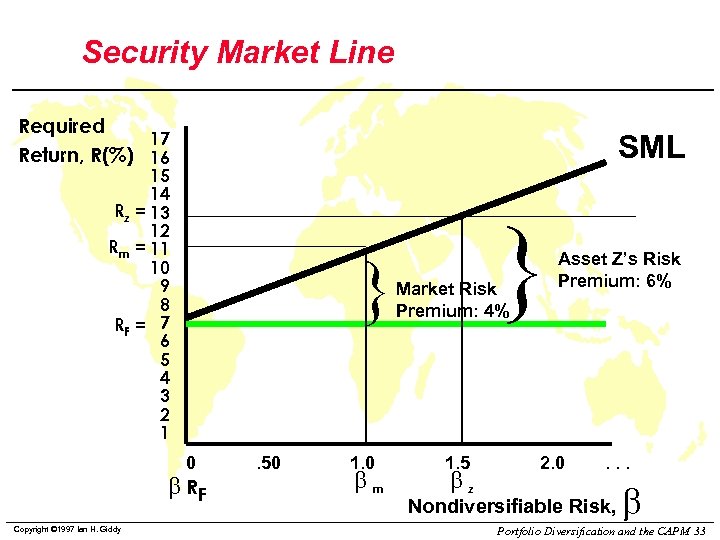 Security Market Line Required 17 Return, R(%) 16 SML 15 14 Rz = 13 12 Rm = 11 10 9 8 RF = 7 6 5 4 3 2 1 } 0 b RF Copyright © 1997 Ian H. Giddy . 50 1. 0 bm } Market Risk Premium: 4% 1. 5 bz Asset Z’s Risk Premium: 6% 2. 0 . . . Nondiversifiable Risk, b Portfolio Diversification and the CAPM 33
Security Market Line Required 17 Return, R(%) 16 SML 15 14 Rz = 13 12 Rm = 11 10 9 8 RF = 7 6 5 4 3 2 1 } 0 b RF Copyright © 1997 Ian H. Giddy . 50 1. 0 bm } Market Risk Premium: 4% 1. 5 bz Asset Z’s Risk Premium: 6% 2. 0 . . . Nondiversifiable Risk, b Portfolio Diversification and the CAPM 33
 The Equation for the CAPM Rj = RF + bj (Rm - RF) where: Rj = RF = bj Rm = = Required return on asset j; Risk-free rate of return Beta Coefficient for asset j; Market return The term [bj(Rm - RF)] is called the risk premium and (Rm-RF) is called the market risk premium Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 34
The Equation for the CAPM Rj = RF + bj (Rm - RF) where: Rj = RF = bj Rm = = Required return on asset j; Risk-free rate of return Beta Coefficient for asset j; Market return The term [bj(Rm - RF)] is called the risk premium and (Rm-RF) is called the market risk premium Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 34
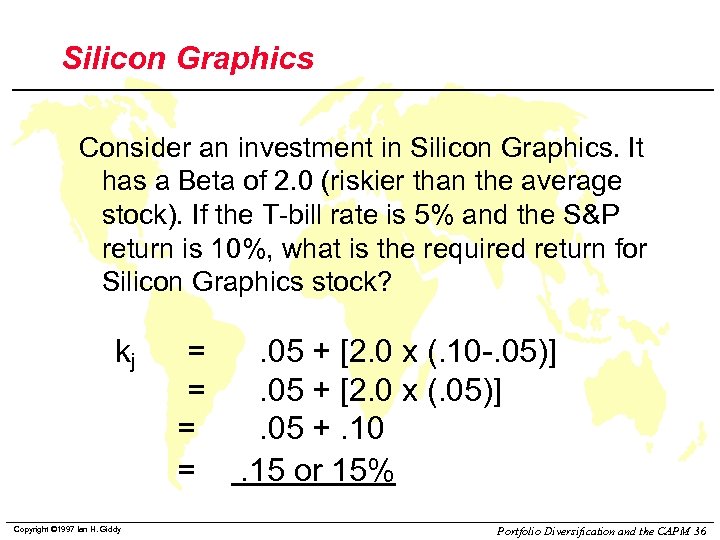 Silicon Graphics Consider an investment in Silicon Graphics. It has a Beta of 2. 0 (riskier than the average stock). If the T-bill rate is 5% and the S&P return is 10%, what is the required return for Silicon Graphics stock? kj Copyright © 1997 Ian H. Giddy = = . 05 + [2. 0 x (. 10 -. 05)]. 05 + [2. 0 x (. 05)]. 05 +. 10. 15 or 15% Portfolio Diversification and the CAPM 36
Silicon Graphics Consider an investment in Silicon Graphics. It has a Beta of 2. 0 (riskier than the average stock). If the T-bill rate is 5% and the S&P return is 10%, what is the required return for Silicon Graphics stock? kj Copyright © 1997 Ian H. Giddy = = . 05 + [2. 0 x (. 10 -. 05)]. 05 + [2. 0 x (. 05)]. 05 +. 10. 15 or 15% Portfolio Diversification and the CAPM 36
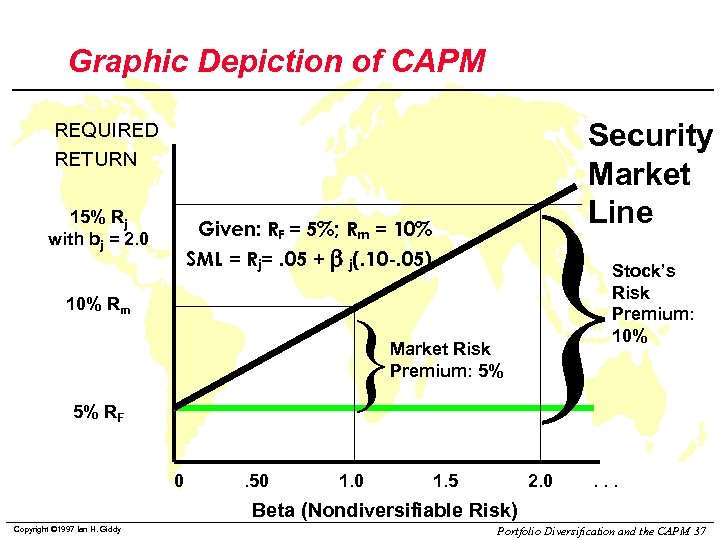 Graphic Depiction of CAPM Security Market Line REQUIRED RETURN 15% Rj with bj = 2. 0 Given: RF = 5%; Rm = 10% SML = Rj=. 05 + b j(. 10 -. 05) 10% Rm } Market Risk Premium: 5% 5% RF 0 . 50 1. 5 } Stock’s Risk Premium: 10% 2. 0 . . . Beta (Nondiversifiable Risk) Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 37
Graphic Depiction of CAPM Security Market Line REQUIRED RETURN 15% Rj with bj = 2. 0 Given: RF = 5%; Rm = 10% SML = Rj=. 05 + b j(. 10 -. 05) 10% Rm } Market Risk Premium: 5% 5% RF 0 . 50 1. 5 } Stock’s Risk Premium: 10% 2. 0 . . . Beta (Nondiversifiable Risk) Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 37
 Interpreting Beta l Market Beta = 1. 0 = average level of risk u. A Beta of. 5 is half as risky as average u. A Beta of 2. 0 is twice as risky as average u. A negative Beta asset moves in opposite direction to market Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 38
Interpreting Beta l Market Beta = 1. 0 = average level of risk u. A Beta of. 5 is half as risky as average u. A Beta of 2. 0 is twice as risky as average u. A negative Beta asset moves in opposite direction to market Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 38
 Finding Beta: Example You have found the following data relative to the stock of the Telmex Corp. and current conditions: Required/expected return Market portfolio return Risk premium for market portfolio = 20% = 11% = 6% What is the Beta of Telmex stock? Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 43
Finding Beta: Example You have found the following data relative to the stock of the Telmex Corp. and current conditions: Required/expected return Market portfolio return Risk premium for market portfolio = 20% = 11% = 6% What is the Beta of Telmex stock? Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 43
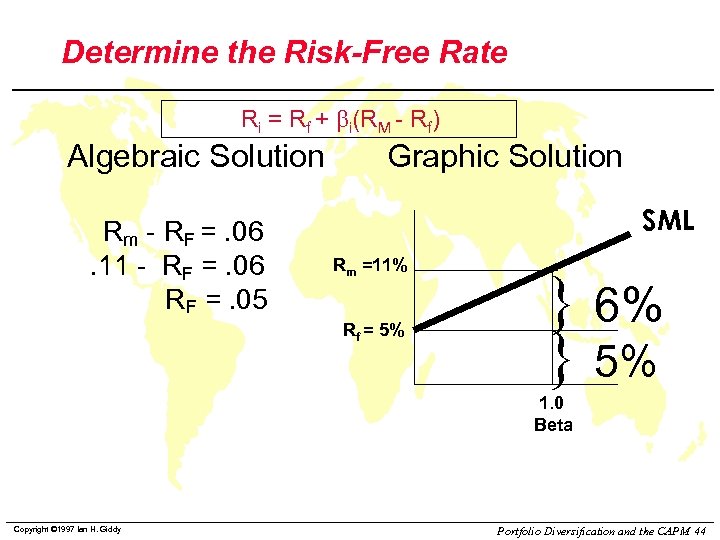 Determine the Risk-Free Rate Ri = Rf + bi(RM - Rf) Algebraic Solution Rm - RF =. 06. 11 - RF =. 06 RF =. 05 Graphic Solution SML Rm =11% Rf = 5% } 6% } 5% 1. 0 Beta Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 44
Determine the Risk-Free Rate Ri = Rf + bi(RM - Rf) Algebraic Solution Rm - RF =. 06. 11 - RF =. 06 RF =. 05 Graphic Solution SML Rm =11% Rf = 5% } 6% } 5% 1. 0 Beta Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 44
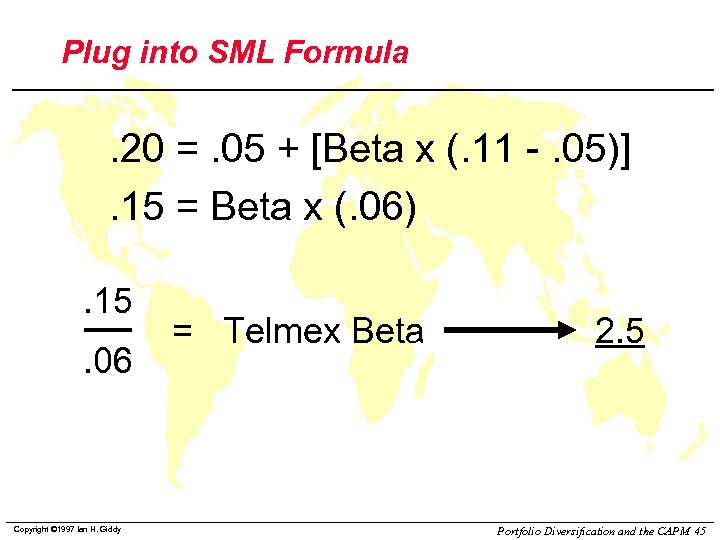 Plug into SML Formula . 20 =. 05 + [Beta x (. 11 -. 05)]. 15 = Beta x (. 06). 15. 06 Copyright © 1997 Ian H. Giddy = Telmex Beta 2. 5 Portfolio Diversification and the CAPM 45
Plug into SML Formula . 20 =. 05 + [Beta x (. 11 -. 05)]. 15 = Beta x (. 06). 15. 06 Copyright © 1997 Ian H. Giddy = Telmex Beta 2. 5 Portfolio Diversification and the CAPM 45
 New York University/ING Barings Portfolio Theory Assignment Prof. Ian Giddy New York University
New York University/ING Barings Portfolio Theory Assignment Prof. Ian Giddy New York University
 Try these problems l Ch 6 u. Problem 12 u. Problems 14 -16 (see p 157) l Ch 7 u. Problem 1 u. Problem 5 Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 47
Try these problems l Ch 6 u. Problem 12 u. Problems 14 -16 (see p 157) l Ch 7 u. Problem 1 u. Problem 5 Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 47
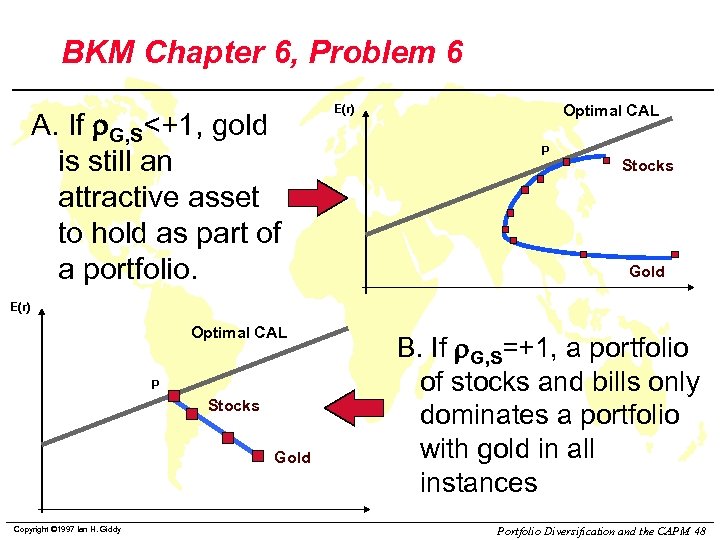 BKM Chapter 6, Problem 6 A. If r. G, S<+1, gold is still an attractive asset to hold as part of a portfolio. Optimal CAL E(r) P Stocks Gold E(r) Optimal CAL P Stocks Gold Copyright © 1997 Ian H. Giddy B. If r. G, S=+1, a portfolio of stocks and bills only dominates a portfolio with gold in all instances Portfolio Diversification and the CAPM 48
BKM Chapter 6, Problem 6 A. If r. G, S<+1, gold is still an attractive asset to hold as part of a portfolio. Optimal CAL E(r) P Stocks Gold E(r) Optimal CAL P Stocks Gold Copyright © 1997 Ian H. Giddy B. If r. G, S=+1, a portfolio of stocks and bills only dominates a portfolio with gold in all instances Portfolio Diversification and the CAPM 48
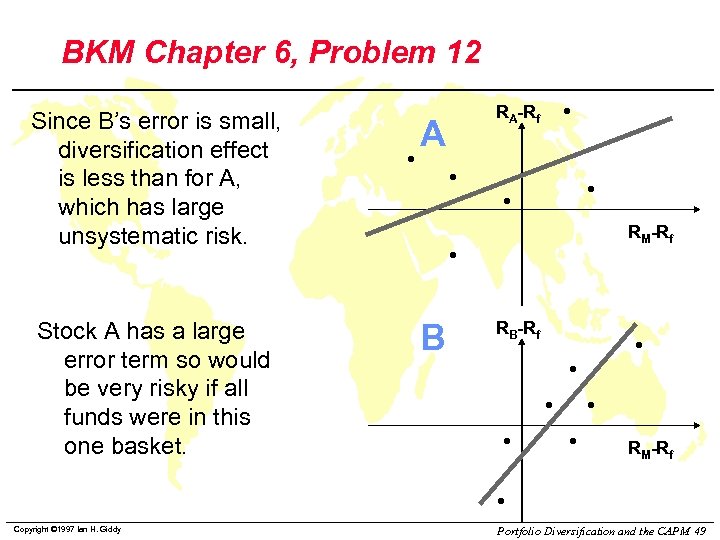 BKM Chapter 6, Problem 12 Since B’s error is small, diversification effect is less than for A, which has large unsystematic risk. Stock A has a large error term so would be very risky if all funds were in this one basket. Copyright © 1997 Ian H. Giddy A RA-Rf RM-Rf B RB-Rf RM-Rf Portfolio Diversification and the CAPM 49
BKM Chapter 6, Problem 12 Since B’s error is small, diversification effect is less than for A, which has large unsystematic risk. Stock A has a large error term so would be very risky if all funds were in this one basket. Copyright © 1997 Ian H. Giddy A RA-Rf RM-Rf B RB-Rf RM-Rf Portfolio Diversification and the CAPM 49
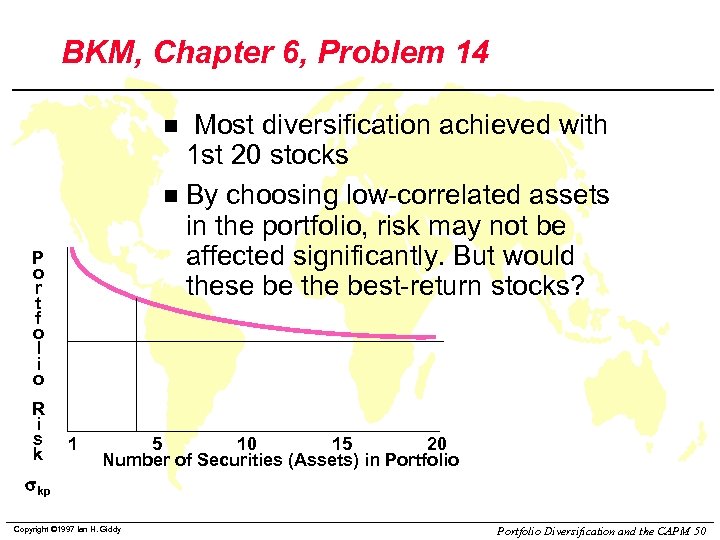 BKM, Chapter 6, Problem 14 Most diversification achieved with 1 st 20 stocks n By choosing low-correlated assets in the portfolio, risk may not be affected significantly. But would these be the best-return stocks? n P o r t f o l i o R i s k 1 5 10 15 20 Number of Securities (Assets) in Portfolio skp Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 50
BKM, Chapter 6, Problem 14 Most diversification achieved with 1 st 20 stocks n By choosing low-correlated assets in the portfolio, risk may not be affected significantly. But would these be the best-return stocks? n P o r t f o l i o R i s k 1 5 10 15 20 Number of Securities (Assets) in Portfolio skp Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 50
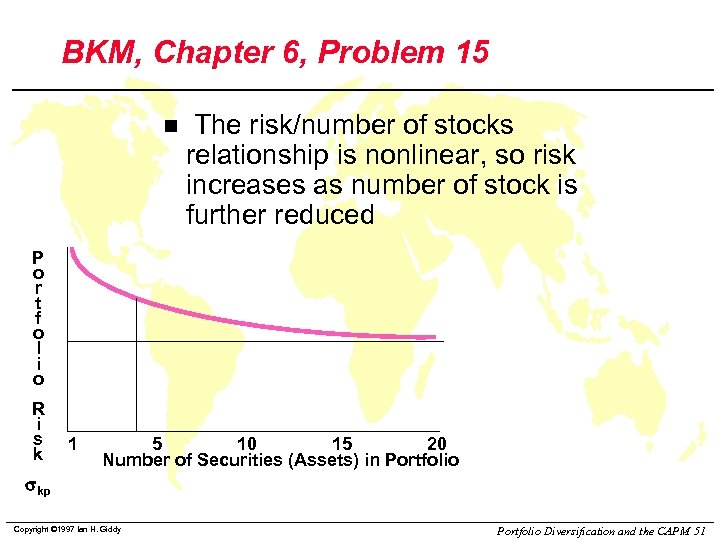 BKM, Chapter 6, Problem 15 n The risk/number of stocks relationship is nonlinear, so risk increases as number of stock is further reduced P o r t f o l i o R i s k 1 5 10 15 20 Number of Securities (Assets) in Portfolio skp Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 51
BKM, Chapter 6, Problem 15 n The risk/number of stocks relationship is nonlinear, so risk increases as number of stock is further reduced P o r t f o l i o R i s k 1 5 10 15 20 Number of Securities (Assets) in Portfolio skp Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 51
 BKM, Chapter 6, Problem 16 E(r) Hennessy’s portfolio n Copyright © 1997 Ian H. Giddy Limiting Hennessy’s holdings may have little impact on the risk of the total portfolio Portfolio Diversification and the CAPM 52
BKM, Chapter 6, Problem 16 E(r) Hennessy’s portfolio n Copyright © 1997 Ian H. Giddy Limiting Hennessy’s holdings may have little impact on the risk of the total portfolio Portfolio Diversification and the CAPM 52
![BKM, Chapter 7, Problem 1 E(RP) = Rf + b[E(RM) - Rf] 20 = BKM, Chapter 7, Problem 1 E(RP) = Rf + b[E(RM) - Rf] 20 =](https://present5.com/presentation/ae593213c30de8edbae62a2139e97475/image-39.jpg) BKM, Chapter 7, Problem 1 E(RP) = Rf + b[E(RM) - Rf] 20 = 5 + b(15 -5) b =15/10 = 1. 5 Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 53
BKM, Chapter 7, Problem 1 E(RP) = Rf + b[E(RM) - Rf] 20 = 5 + b(15 -5) b =15/10 = 1. 5 Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 53
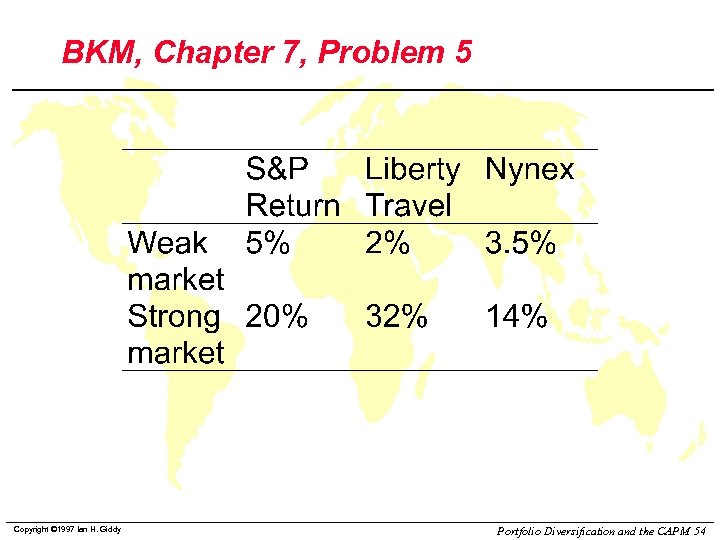 BKM, Chapter 7, Problem 5 Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 54
BKM, Chapter 7, Problem 5 Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 54
 BKM, Chapter 7, Problem 5 A ) The beta is the change in the stock return per change in the market return. Therefore: b. Aggressive = (2 -32)/(5 -20) = 2. 00 b. Defensive = (3. 5 -14)/(5 -20) =. 70 B ) The expected return is an average of the two possible outcomes: E(RAgg. ) =. 5(2+32) = 17% E(RDef. ) =. 5(3. 5+14) = 8. 75% Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 55
BKM, Chapter 7, Problem 5 A ) The beta is the change in the stock return per change in the market return. Therefore: b. Aggressive = (2 -32)/(5 -20) = 2. 00 b. Defensive = (3. 5 -14)/(5 -20) =. 70 B ) The expected return is an average of the two possible outcomes: E(RAgg. ) =. 5(2+32) = 17% E(RDef. ) =. 5(3. 5+14) = 8. 75% Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 55
 BKM, Chapter 7, Problem 5 C / The SML is determined by the market expected return of. 5(20+5) = 12. 5%, with a beta of 1, and the bill return of 8%. Therefore, the equation for the security market line is: E(R) = 8 + b(12. 5 - 8) Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 56
BKM, Chapter 7, Problem 5 C / The SML is determined by the market expected return of. 5(20+5) = 12. 5%, with a beta of 1, and the bill return of 8%. Therefore, the equation for the security market line is: E(R) = 8 + b(12. 5 - 8) Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 56
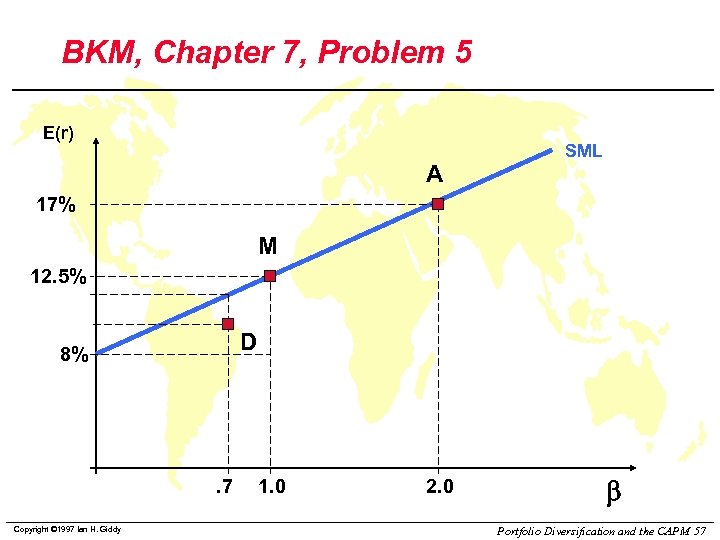 BKM, Chapter 7, Problem 5 E(r) A SML 17% M 12. 5% D 8% . 7 Copyright © 1997 Ian H. Giddy 1. 0 2. 0 b Portfolio Diversification and the CAPM 57
BKM, Chapter 7, Problem 5 E(r) A SML 17% M 12. 5% D 8% . 7 Copyright © 1997 Ian H. Giddy 1. 0 2. 0 b Portfolio Diversification and the CAPM 57
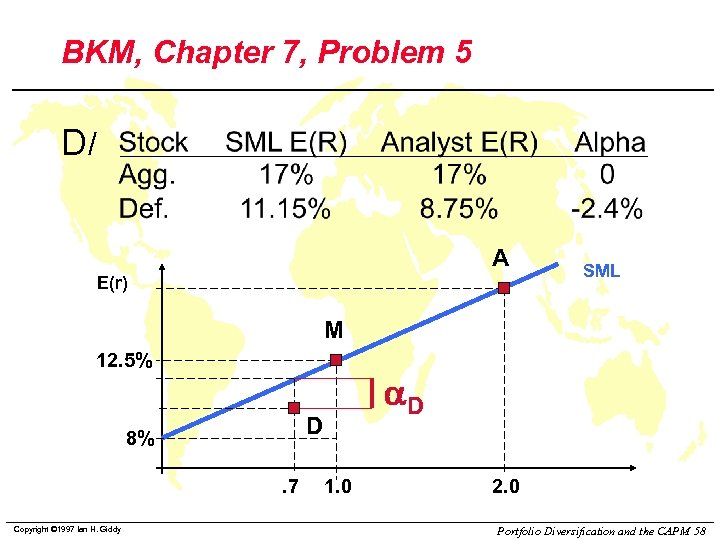 BKM, Chapter 7, Problem 5 D/ A E(r) SML M 12. 5% D 8%. 7 Copyright © 1997 Ian H. Giddy a. D 1. 0 2. 0 Portfolio Diversification and the CAPM 58
BKM, Chapter 7, Problem 5 D/ A E(r) SML M 12. 5% D 8%. 7 Copyright © 1997 Ian H. Giddy a. D 1. 0 2. 0 Portfolio Diversification and the CAPM 58
 BKM, Chapter 7, Problem 5 E / The hurdle rate is determined by the project beta. 7. The correct discount rate is 11. 15%, the fair return on the defensive stock. Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 59
BKM, Chapter 7, Problem 5 E / The hurdle rate is determined by the project beta. 7. The correct discount rate is 11. 15%, the fair return on the defensive stock. Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 59
 Equity Risk and Return: Summary Investors diversify, because you get a better return for a given risk. l There is a fully-diversified “market portfolio” that we should all choose l The risk of an individual asset can be measured by how much risk it adds to the “market portfolio” l The CAPM tells us how the required return relates to the relevant risk. l Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 60
Equity Risk and Return: Summary Investors diversify, because you get a better return for a given risk. l There is a fully-diversified “market portfolio” that we should all choose l The risk of an individual asset can be measured by how much risk it adds to the “market portfolio” l The CAPM tells us how the required return relates to the relevant risk. l Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 60
 Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 61
Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 61
 www. giddy. org Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 62
www. giddy. org Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 62
 Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 63
Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 63
 www. giddy. org Ian Giddy NYU Stern School of Business Tel 212 -998 -0704; Fax 212 -995 -4220 igiddy@stern. nyu. edu http: //www. giddy. org Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 64
www. giddy. org Ian Giddy NYU Stern School of Business Tel 212 -998 -0704; Fax 212 -995 -4220 igiddy@stern. nyu. edu http: //www. giddy. org Copyright © 1997 Ian H. Giddy Portfolio Diversification and the CAPM 64


