Converting Macromolecular Regulatory Models from Deterministic to Stochastic

Converting Macromolecular Regulatory Models from Deterministic to Stochastic Formulation Pengyuan Wang, Ranjit Randhawa, Clifford A. Shaffer, Yang Cao, and William T. Baumann Virginia Tech, Blacksburg VA

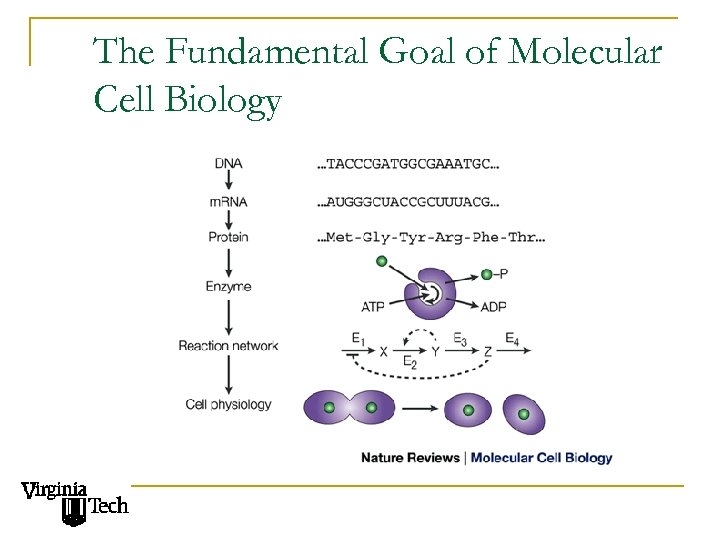The Fundamental Goal of Molecular Cell Biology

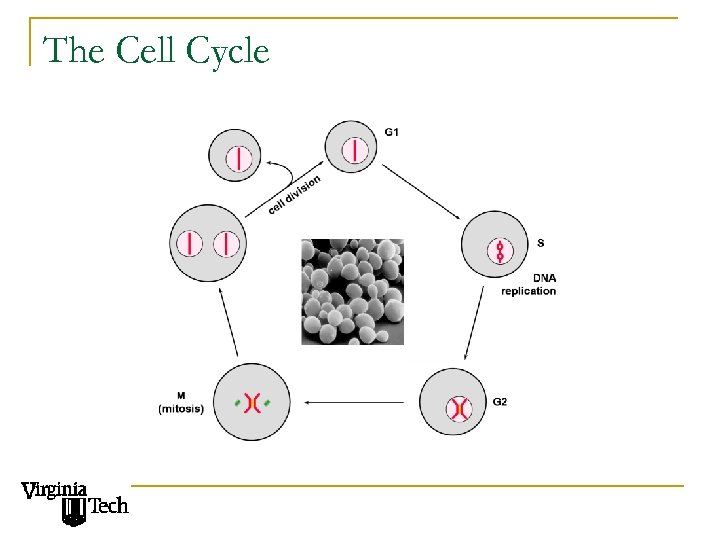The Cell Cycle

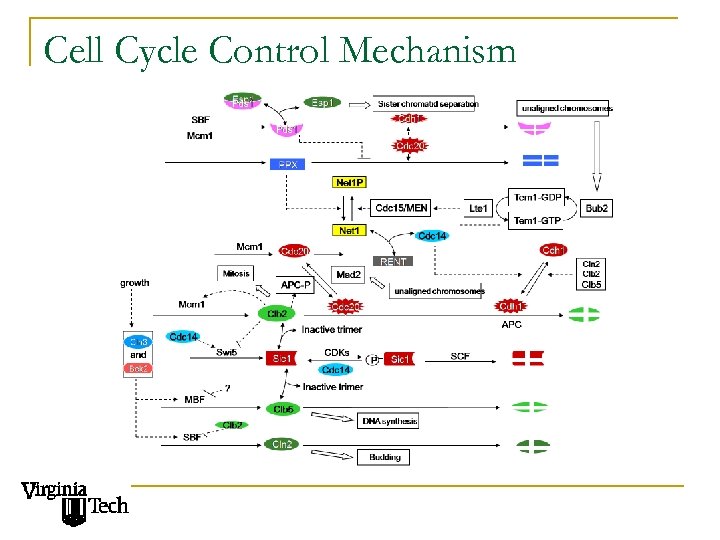Cell Cycle Control Mechanism

Modeling Techniques n One method: Use ODEs that describe the rate at which each protein concentration changes q Protein A degrades protein B: … with initial condition [A](0) = A 0. q Parameter c determines the rate of degradation. Sometimes modelers use “creative” rate laws to approximate subsystems

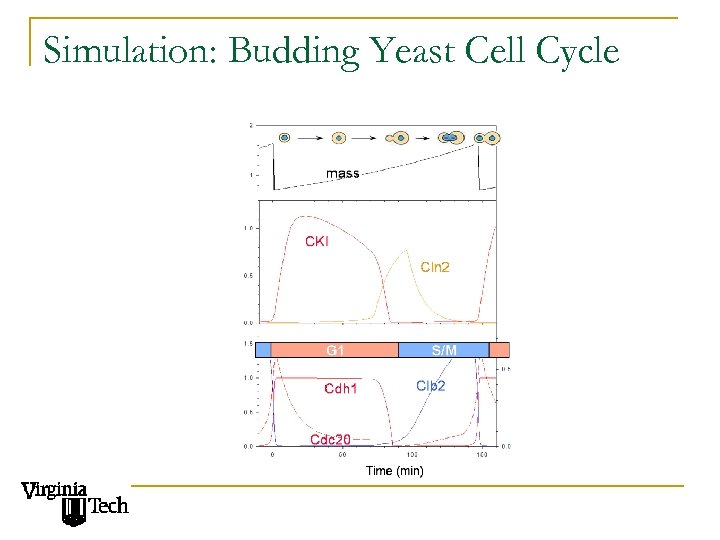Simulation: Budding Yeast Cell Cycle

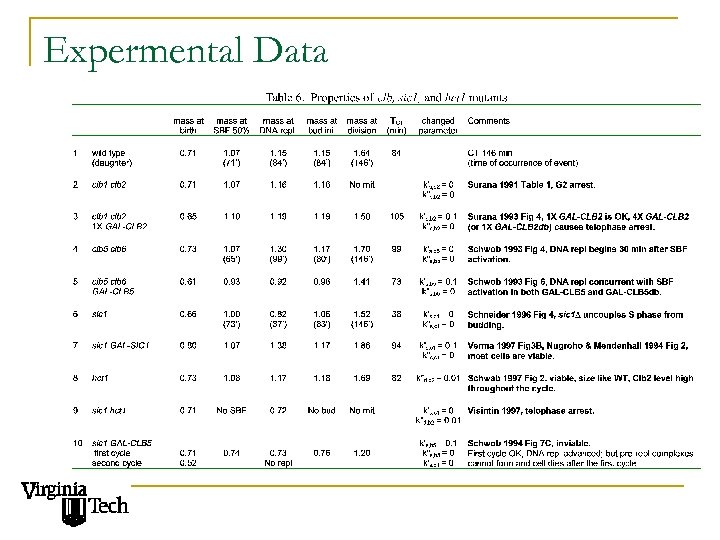Expermental Data

Putting it Together

Chen/Tyson Budding Yeast Model n n n Contains over 30 ODEs, some nonlinear. Events can cause concentrations to be reset. About 140 rate constant parameters q Most are unavailable from experiment and must set by the modeler

Fundamental Activities of the Modeler n Collect information q n Define/modify models q n A user interface problem Run simulations q n Search literature (databases), Lab notebooks Equation solvers (ODEs, PDEs, deterministic, stochastic) Compare simulation results to experimental data q Analysis

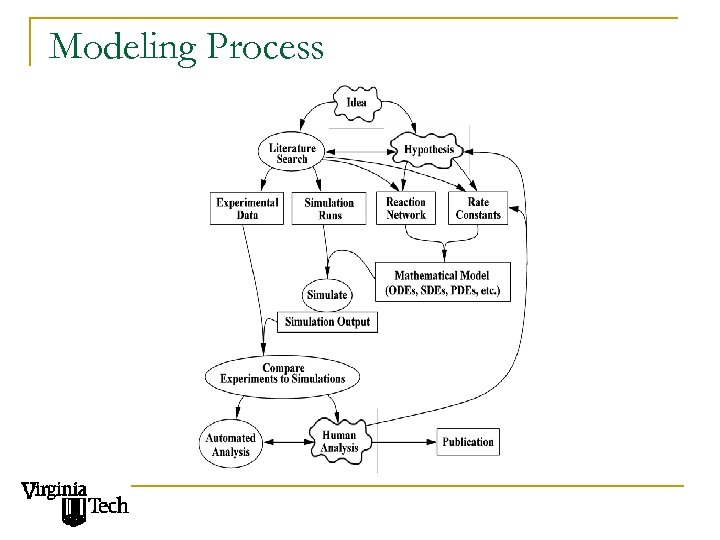Modeling Process

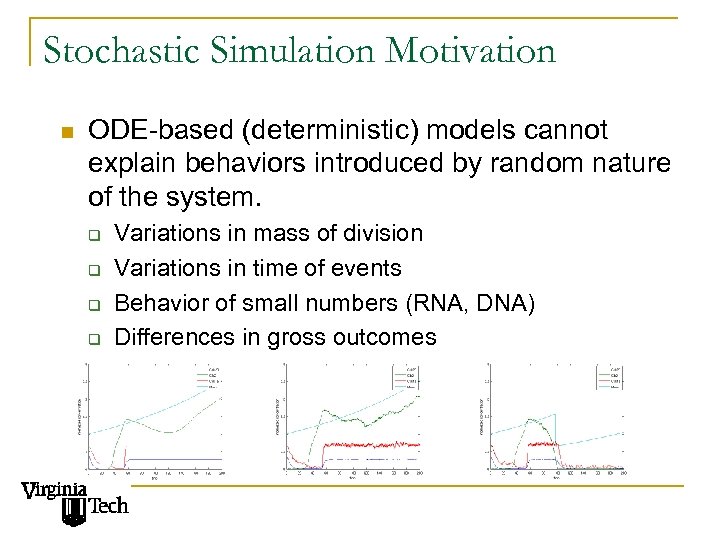Stochastic Simulation Motivation n ODE-based (deterministic) models cannot explain behaviors introduced by random nature of the system. q q Variations in mass of division Variations in time of events Behavior of small numbers (RNA, DNA) Differences in gross outcomes

Gillespie’s Stochastic Simulation Algorithm (SSA) n n There is a population for each chemical species There is a “propensity” for each reaction, in part determined by population Each reaction changes population for associated species Loop: q q n Pick next reaction (random, propensity) Update populations, propensities Slow, there approximations to speed it up

Question n Given an existing deterministic model, how do we convert it to a formulation capable of stochastic simulation? q q n Can this be automated? Is there a fundamental difference in representation? SSA is known to be CPU-intensive. How much computation resource is really needed to simulate the converted model stochastically?

Relation between the Two Formulations n n n In common: both models describe the same reaction network. Difference: the reaction rate equation is replaced by a propensity function describing how likely that the reaction will fire in next unit time. Connection: although they have different physical meanings, propensity function shares the same expression as corresponding reaction rate equation (written in number of molecules). q Caveat: except for the “creative” rate laws

Missing Information n Usually ODE models are written in terms of normalized concentrations. Thus they need to be converted to models in terms of number of molecules (population). Some information is missing q q q Characteristic concentration Explicit definition of units Volume of the container.

Conversion n The relation between normalized concentration, real concentration and population of a species:

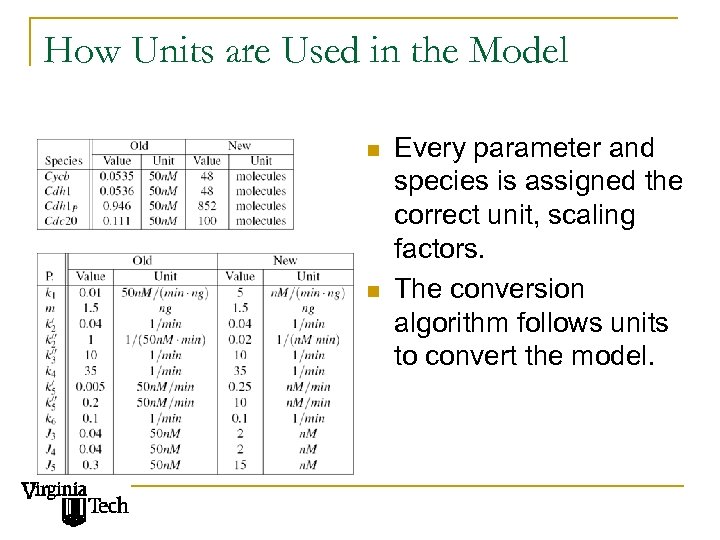How Units are Used in the Model n n Every parameter and species is assigned the correct unit, scaling factors. The conversion algorithm follows units to convert the model.

The Challenge n n n Assigning correct units to species and parameters is difficult because all the species, parameters, and reactions are connected by the whole reaction network. Once the modeler is forced to provide the “complete” specification, the conversion can be automated Caveats: q q “Creative” rate laws Events

Events Need Extra Care /*deterministic events*/ If (A>threshold) Then {event is triggered}. (Here “>” means rising above a threshold) n /*stochastic events*/ If (Athreshold) Then {event is triggered; minimum=A}. (we ask for A truly rising from a low value, not happening to rise by oscillation. ) Except for events, all other parts of the model are automatically converted by Jig. Cell.

Conversion Tool n n Part of the Jig. Cell modeling suite Automatically checks unit consistency inside the model q q q Every two quantities (a parameter, a species, or the result of a sub-expression) connected by + or in the rate law equation must have same units. All species whose values are changed by the same reaction must have the same units. The unit of the result from the rate law equation must be equal to the unit of the reaction rate.

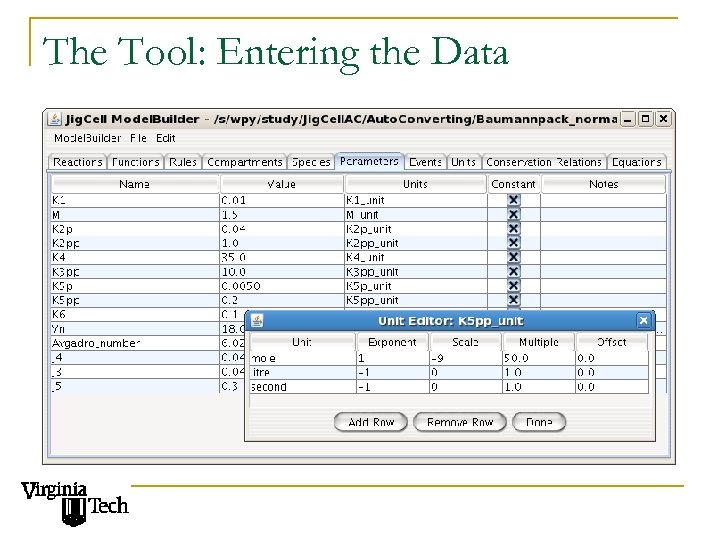The Tool: Entering the Data

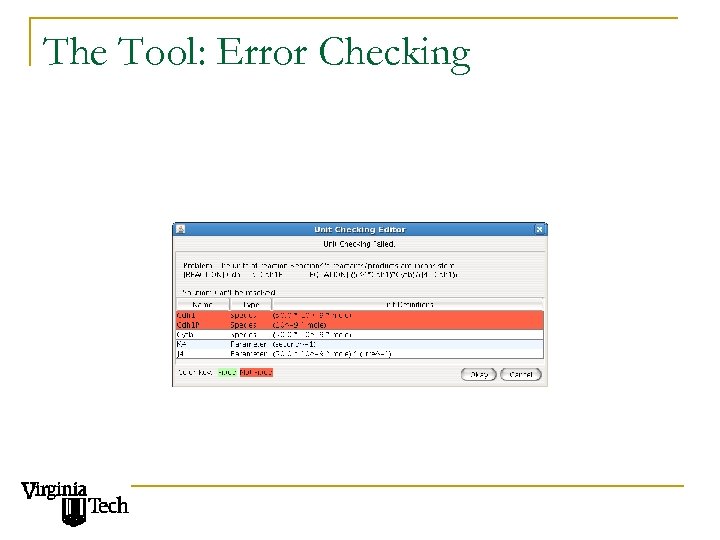The Tool: Error Checking

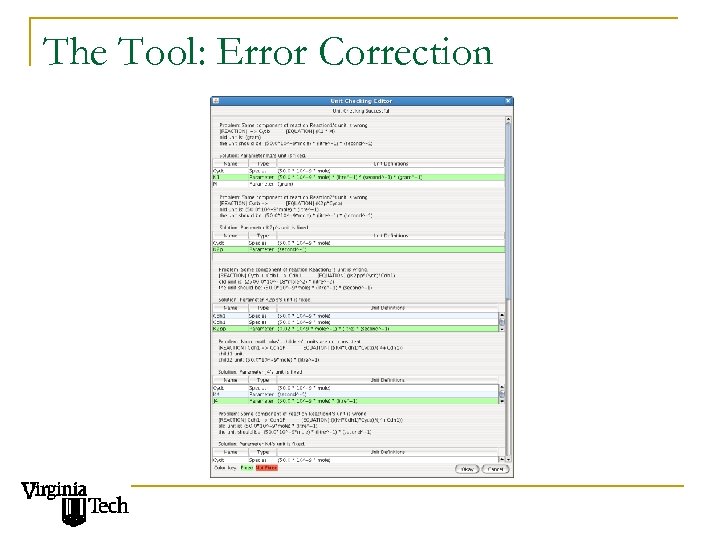The Tool: Error Correction

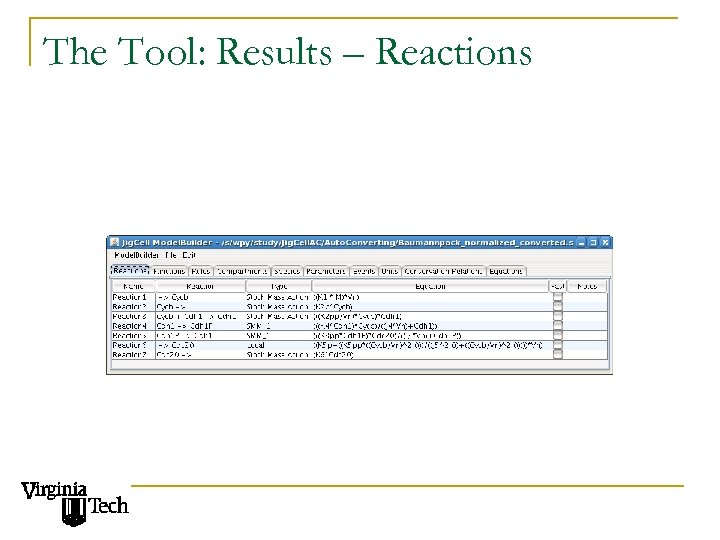The Tool: Results – Reactions

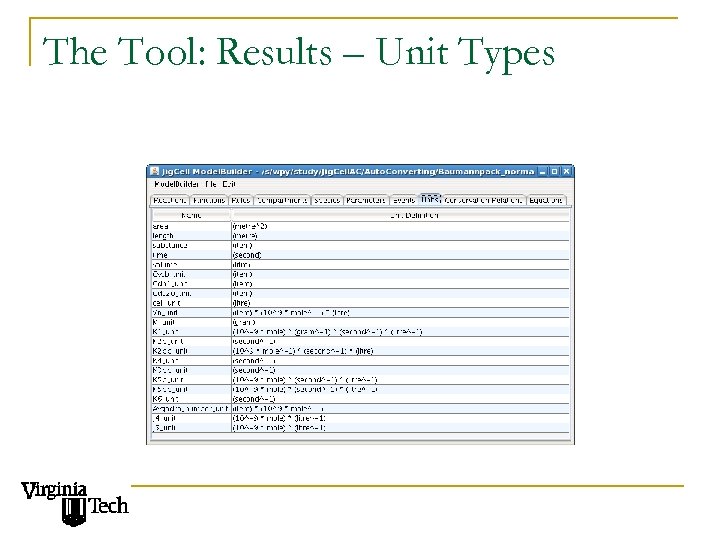The Tool: Results – Unit Types

Simulation Experiments: Setup n Model: q q n Data: q q n A simplified cell cycle model A full-sized budding yeast cell cycle model* 38 of 45 species in full-sized model use realistic characteristic concentration found in the literature. Cell volume is set to 50 f. L. Simulator: q Stoch. Kit, a C++ stochastic simulator integrated into Jig. Cell, running SSA.

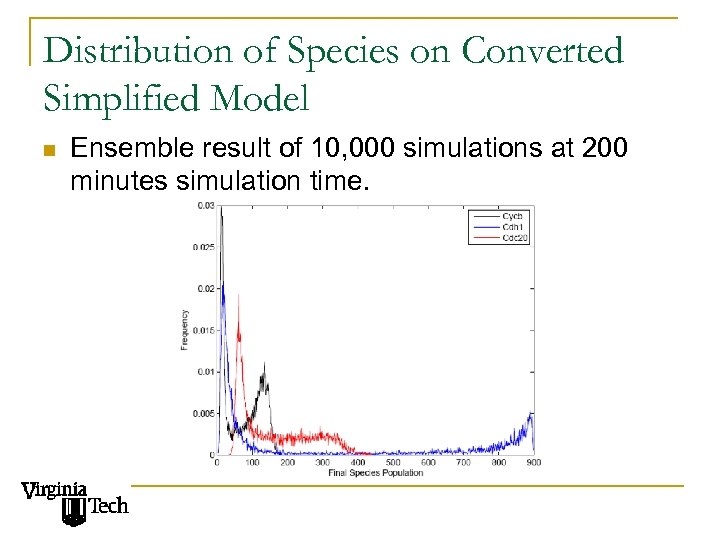Distribution of Species on Converted Simplified Model n Ensemble result of 10, 000 simulations at 200 minutes simulation time.

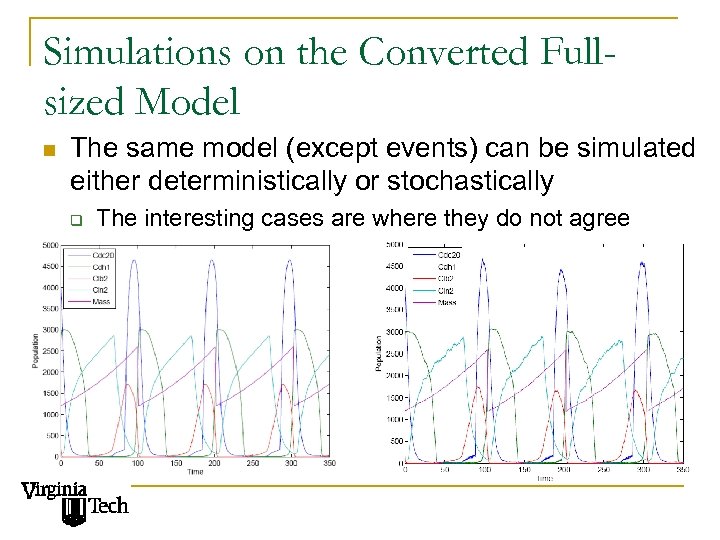Simulations on the Converted Fullsized Model n The same model (except events) can be simulated either deterministically or stochastically q The interesting cases are where they do not agree

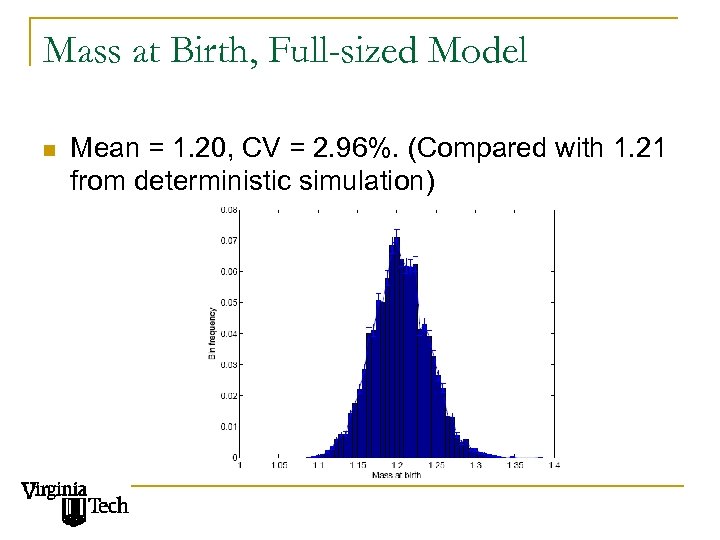Mass at Birth, Full-sized Model n Mean = 1. 20, CV = 2. 96%. (Compared with 1. 21 from deterministic simulation)

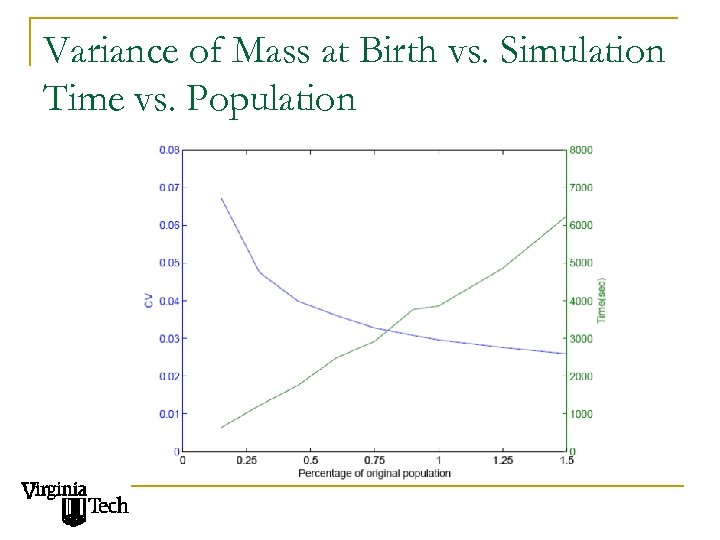Variance of Mass at Birth vs. Simulation Time vs. Population

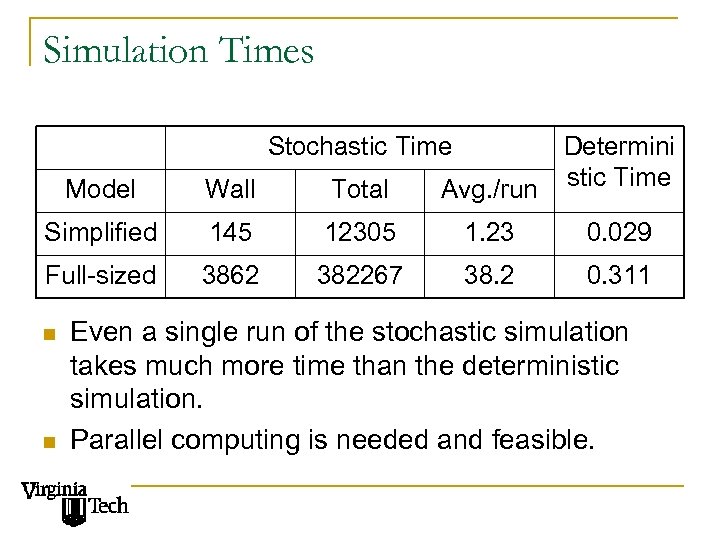Simulation Times Stochastic Time Determini Avg. /run stic Time Model Wall Total Simplified 145 12305 1. 23 0. 029 Full-sized 3862 382267 38. 2 0. 311 n n Even a single run of the stochastic simulation takes much more time than the deterministic simulation. Parallel computing is needed and feasible.

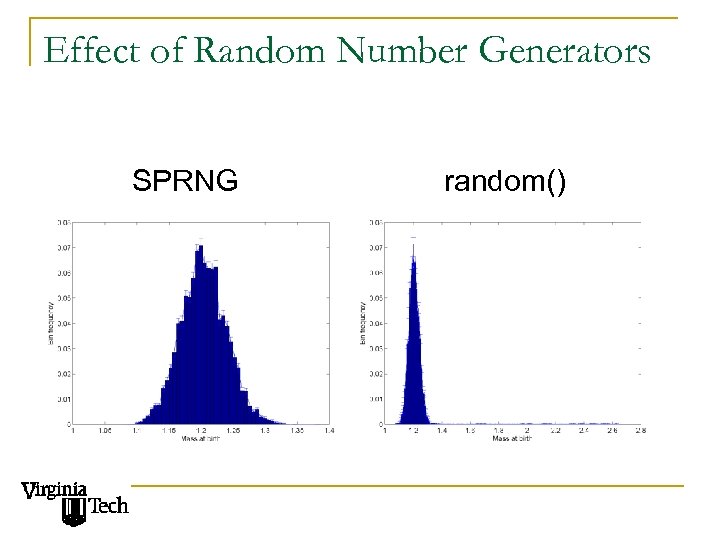Effect of Random Number Generators SPRNG random()

Conclusions n Improved support for the conversion process q n Deterministic and stochastic formulations are not fundamentally different q n The Jig. Cell conversion tool Deterministic modelers like to take short cuts Real experience with stochastic simulations on meaningful models q q q Events Runtimes Approximation results

Future Work n n Initial conditions distribution Truly growing volume: q q n Our previous model had growing mass but fixed volume, which is not realistic Change to growing volume will change the reaction rate (propensity function) Simulations on mutants of particular interest