c8c07ffb14352ff6888d7762f268efec.ppt
- Количество слайдов: 28

Conversion Driven Design of Binary to Mixed Radix Circuits Ashur Rafiev, Julian Murphy, Danil Sokolov, Alex Yakovlev School of EECE, Newcastle University, UK {ashur. rafiev, j. p. murphy, danil. sokolov, alex. yakovlev} @ ncl. ac. uk 1 ICCD 2008

Outline Æ Switching Balanced Codes Conversion Driven Design (CDD) Motivation Conversion Basics Bitwise Approach Bitwise Gate Grouping Algorithm Artificial Combinational Loops Problem Operandwise Approach Operandwise Gate Grouping Algorithm Benchmark Results Conclusions Outline 2 ICCD 2008

Switching Balanced Codes M-of-N data encoding: data signal is represented with • N wires • M of them are active (high) Return-to-zero (RTZ) protocol: data signals are separated with dummy signals (spacers) Application areas: • Security • Asynchronous system design • Network-on-chip communication Switching Balanced Codes 3 ICCD 2008
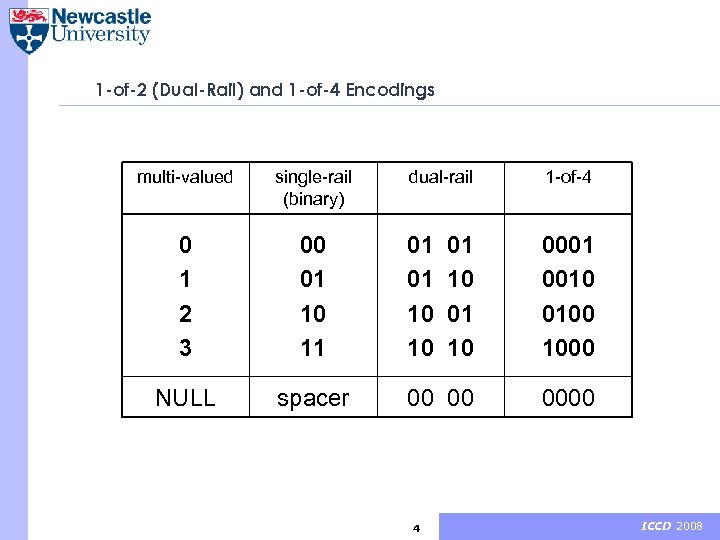
1 -of-2 (Dual-Rail) and 1 -of-4 Encodings multi-valued single-rail (binary) 0 1 2 3 00 01 10 11 NULL spacer dual-rail 1 -of-4 01 01 10 10 01 10 0001 0010 0100 1000 0000 4 ICCD 2008

Outline Switching Balanced Codes Æ Conversion Driven Design Motivation Conversion Basics Bitwise Approach Bitwise Gate Grouping Algorithm Artificial Combinational Loops Problem Operandwise Approach Operandwise Gate Grouping Algorithm Benchmark Results Conclusions Outline 5 ICCD 2008

Conversion Driven Design: Motivation + Higher radix signals consume less power and reduce crosstalk effect – Require multi-valued logic synthesis + Some tools and techniques è Reuse existing popular design tools for multivalued system design already exist (e. g. MV-SIS) – Moving away from the RTL design flow is frequently frowned upon by industry 6 ICCD 2008
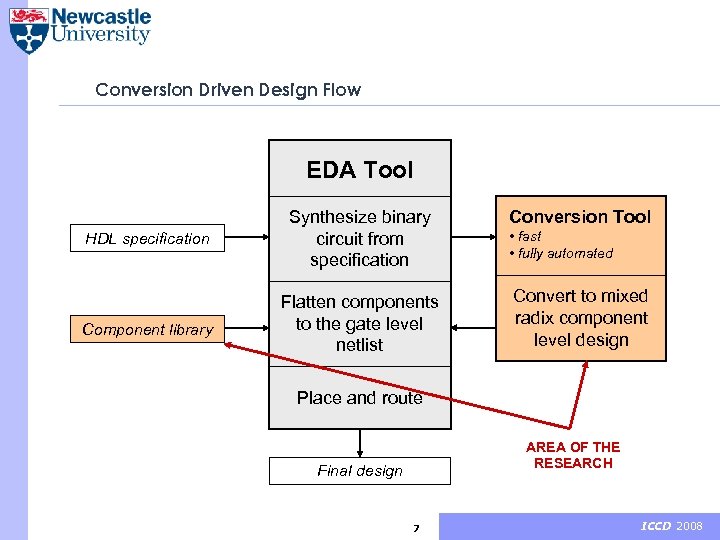
Conversion Driven Design Flow EDA Tool Conversion Tool HDL specification Synthesize binary circuit from specification Component library Flatten components to the gate level netlist Convert to mixed radix component level design • fast • fully automated Place and route AREA OF THE RESEARCH Final design 7 ICCD 2008
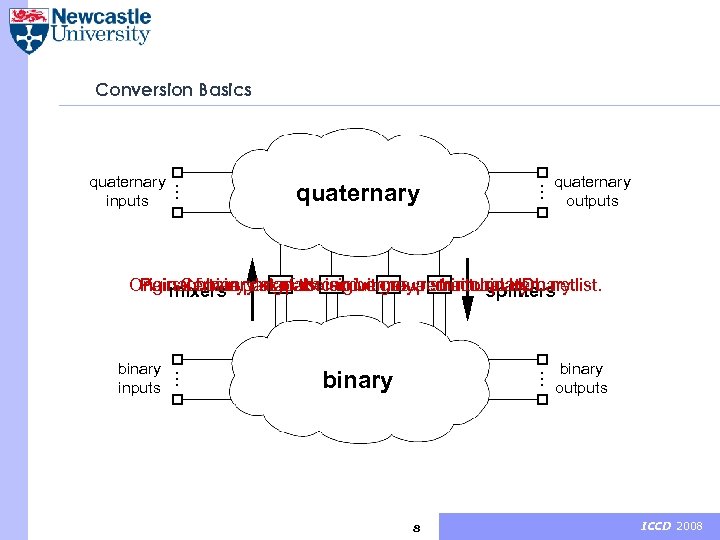
Conversion Basics quaternary outputs … … quaternary inputs … Original binarypart of … can be grouped intobinary. netlist. Pairs. Certain datapath is given as a structural HDL of binary signals circuit may remain quaternary. the mixers splitters binary outputs binary … … binary inputs 8 ICCD 2008

Conversion Basics Signal converters: § A splitter converts one quaternary signal into two binary. § A mixer converts two binary signals into one quaternary. § The way the signals (gates) are grouped determines the efficiency of the conversion, therefore the conversion problem corresponds directly to the gate grouping problem. 9 ICCD 2008

Outline Switching Balanced Codes Conversion Driven Design Motivation Conversion Basics Æ Bitwise Approach Bitwise Gate Grouping Algorithm Artificial Combinational Loops Problem Operandwise Approach Operandwise Gate Grouping Algorithm Benchmark Results Conclusions Outline 10 ICCD 2008
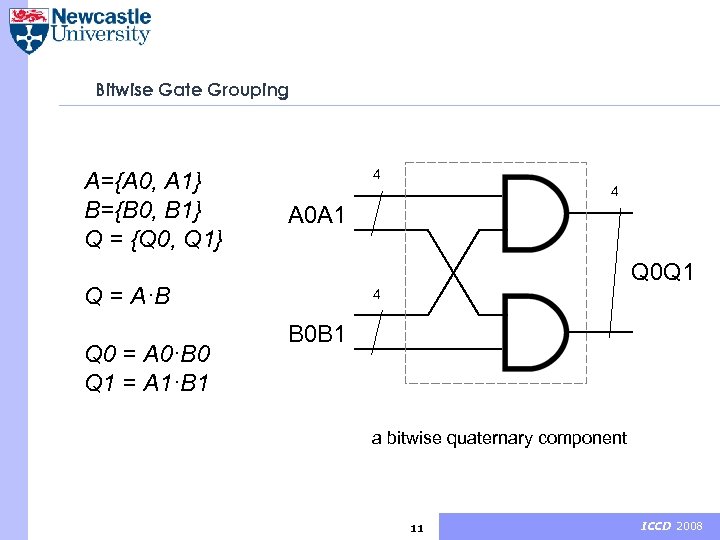
Bitwise Gate Grouping A={A 0, A 1} B={B 0, B 1} Q = {Q 0, Q 1} 4 4 A 0 A 1 Q 0 Q 1 Q = A·B Q 0 = A 0·B 0 Q 1 = A 1·B 1 4 B 0 B 1 a bitwise quaternary component 11 ICCD 2008

Bitwise Gate Grouping Algorithm § Uses heuristics to extract bitwise meaning of signals from the flat netlist. • Input and output port grouping is given • Algorithm is iterative, based on breadth-first search • Bitwise Regularity Ratio is used as an estimation criteria. It is calculated for each gate pair on each iteration. Bitwise Regularity Ratio (BRR) depends on how many quaternary links a pair of gates can form with respect to the state of the conversion on the given iteration. 12 ICCD 2008
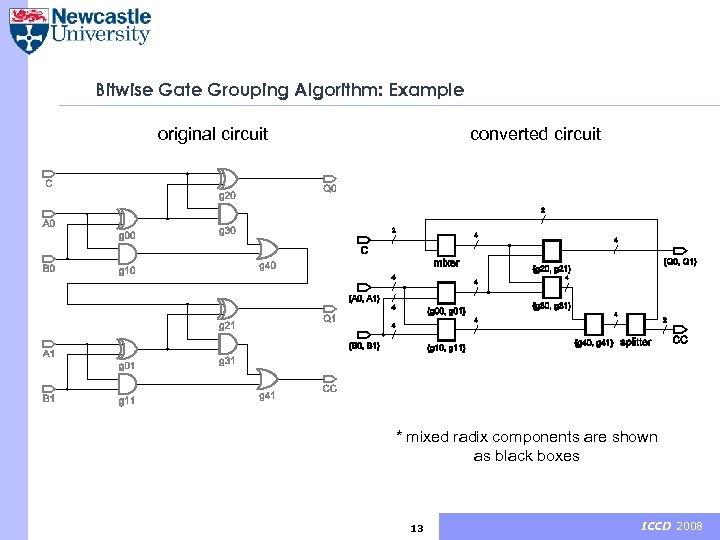
Bitwise Gate Grouping Algorithm: Example original circuit converted circuit BRR=2 BRR=1 * mixed radix components are shown as black boxes 13 ICCD 2008
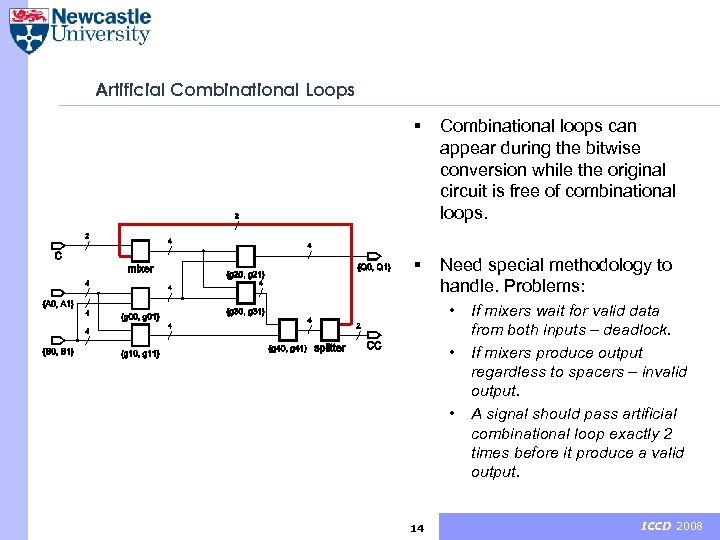
Artificial Combinational Loops § Combinational loops can appear during the bitwise conversion while the original circuit is free of combinational loops. § Need special methodology to handle. Problems: • • • 14 If mixers wait for valid data from both inputs – deadlock. If mixers produce output regardless to spacers – invalid output. A signal should pass artificial combinational loop exactly 2 times before it produce a valid output. ICCD 2008

Bitwise Gate Grouping Disadvantages of the algorithm: § Computational cost O(N) = 2 N 2 log 22 N, N is a number of gates in the original circuit. Disadvantages of the approach: § Inefficient for circuits without bitwise nature of signals, e. g. S-boxes. § The algorithm can produce combinational loops. Bitwise (naive) approach is inefficient for CDD. 15 ICCD 2008

Outline Switching Balanced Codes Conversion Driven Design Motivation Conversion Basics Bitwise Approach Bitwise Gate Grouping Algorithm Artificial Combinational Loops Problem Æ Operandwise Approach Operandwise Gate Grouping Algorithm Benchmark Results Conclusions Outline 16 ICCD 2008
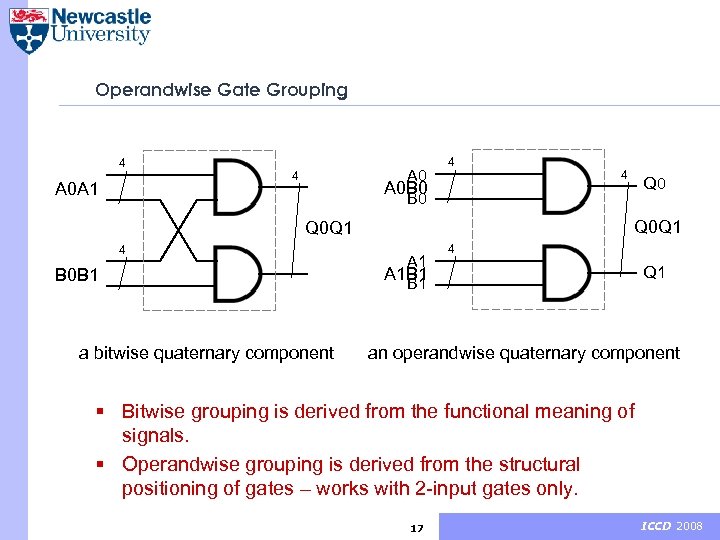
Operandwise Gate Grouping 4 A 0 A 1 A 0 B 0 4 4 4 Q 0 Q 1 4 B 0 B 1 a bitwise quaternary component Q 0 A 1 B 1 4 Q 1 an operandwise quaternary component § Bitwise grouping is derived from the functional meaning of signals. § Operandwise grouping is derived from the structural positioning of gates – works with 2 -input gates only. 17 ICCD 2008
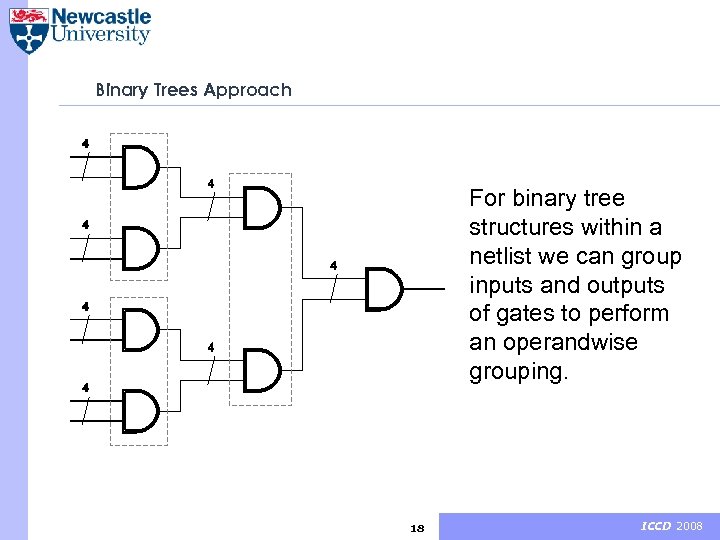
Binary Trees Approach For binary tree structures within a netlist we can group inputs and outputs of gates to perform an operandwise grouping. 18 ICCD 2008
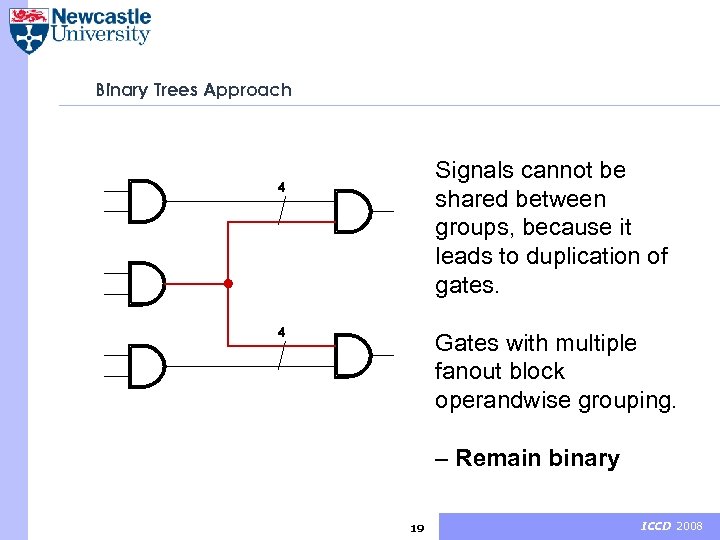
Binary Trees Approach Signals cannot be shared between groups, because it leads to duplication of gates. Gates with multiple fanout block operandwise grouping. – Remain binary 19 ICCD 2008
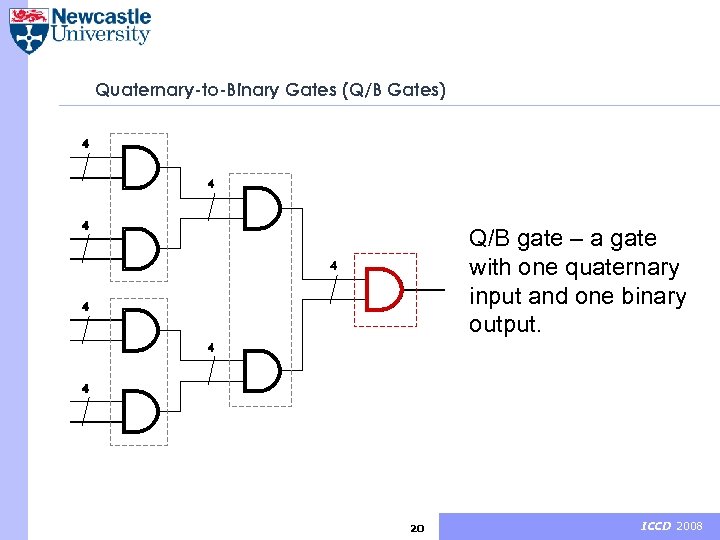
Quaternary-to-Binary Gates (Q/B Gates) Q/B gate – a gate with one quaternary input and one binary output. 20 ICCD 2008
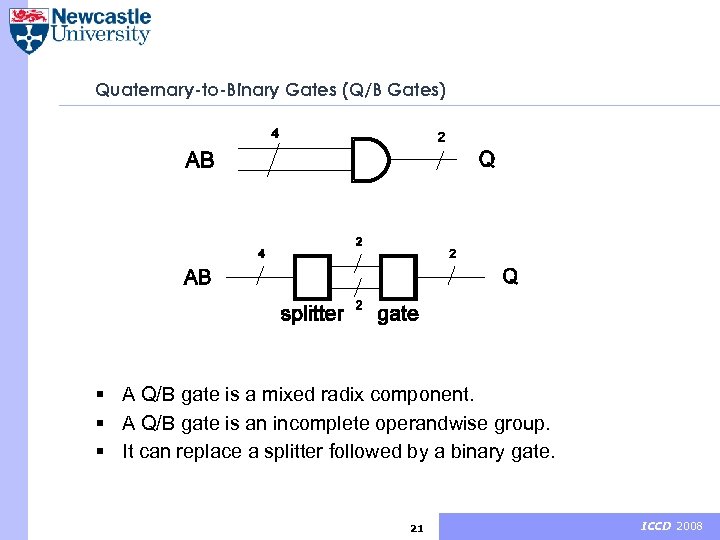
Quaternary-to-Binary Gates (Q/B Gates) § A Q/B gate is a mixed radix component. § A Q/B gate is an incomplete operandwise group. § It can replace a splitter followed by a binary gate. 21 ICCD 2008

Operandwise Gate Grouping Algorithm § Phase I: group all signals regardless of gate fanouts (some gates will be duplicated). § Output ports can be grouped arbitrarily. § Phase II: analyse duplicates and discard groups leading to duplication. § Phase III: insert signal converters and Q/B gates. Computational cost of the algorithm is O(N) = 3 N, where N is a number of gates in the original circuit. 22 ICCD 2008
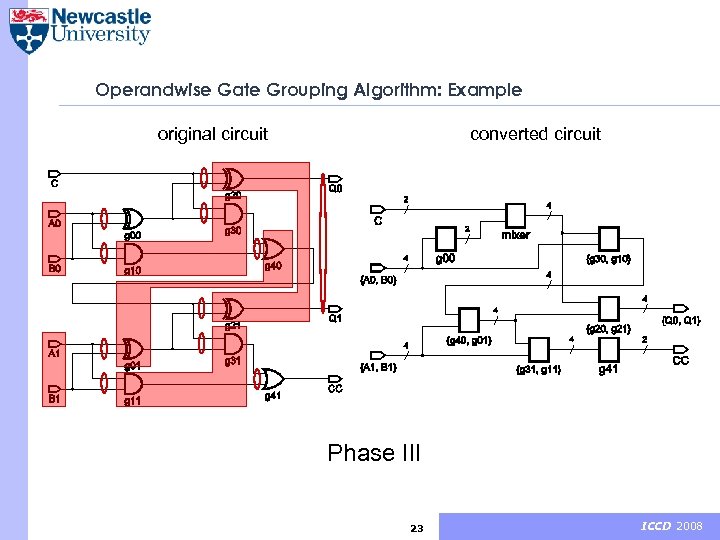
Operandwise Gate Grouping Algorithm: Example original circuit converted circuit Phase III II I 23 ICCD 2008

Operandwise Gate Grouping Advantages of the algorithm: § Low computational cost. § It is highly modular: one can add more passes to the algorithm to increase efficiency of the conversion. Disadvantages of the algorithm: § Can produce significant “fractioning” of binary and quaternary parts of the circuit increasing the number of signal converters required. 24 ICCD 2008
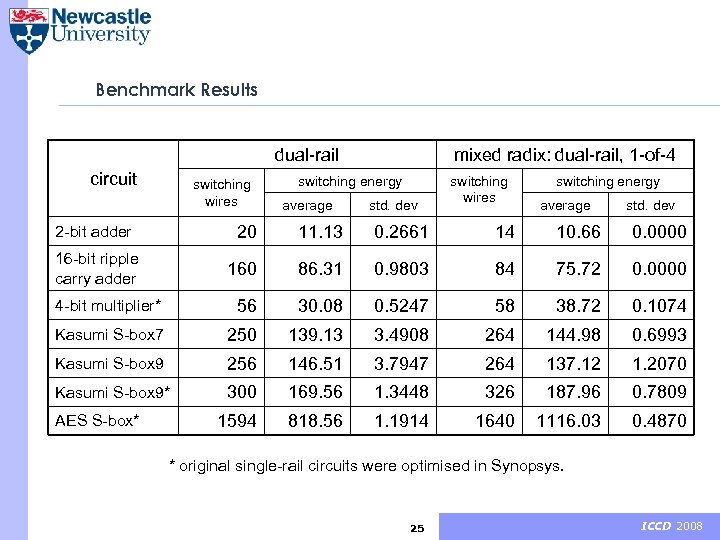
Benchmark Results dual-rail circuit switching wires mixed radix: dual-rail, 1 -of-4 switching energy average std. dev switching wires switching energy average std. dev 20 11. 13 0. 2661 14 10. 66 0. 0000 160 86. 31 0. 9803 84 75. 72 0. 0000 4 -bit multiplier* 56 30. 08 0. 5247 58 38. 72 0. 1074 Kasumi S-box 7 250 139. 13 3. 4908 264 144. 98 0. 6993 Kasumi S-box 9 256 146. 51 3. 7947 264 137. 12 1. 2070 Kasumi S-box 9* 300 169. 56 1. 3448 326 187. 96 0. 7809 1594 818. 56 1. 1914 1640 1116. 03 0. 4870 2 -bit adder 16 -bit ripple carry adder AES S-box* * original single-rail circuits were optimised in Synopsys. 25 ICCD 2008

Outline Switching Balanced Codes Conversion Driven Design Motivation Conversion Basics Bitwise Approach Bitwise Gate Grouping Algorithm Artificial Combinational Loops Problem Operandwise Approach Operandwise Gate Grouping Algorithm Benchmark Results Æ Conclusions Outline 26 ICCD 2008

Conclusions § Conversion driven design technique was suggested in order to reuse popular EDA tools for MVL synthesis. § Binary and quaternary mixed radix was selected to improve the efficiency of the conversion. § Two conversion (gate grouping) algorithms were implemented analysed. • Bitwise approach is not efficient for CDD • Operandwise approach is fast and flexible but not efficient enough in terms of saving switching energy. Future work: § Improve operandwise component implementations. § Add more heuristics to the operandwise algorithm to increase the efficiency of the conversion. 27 ICCD 2008

The End Thank you! Questions? 28 ICCD 2008
c8c07ffb14352ff6888d7762f268efec.ppt