CONTROL AUTOMATICO CAPITULO VII ESTABILIDAD EN EL DOMINIO

CONTROL AUTOMATICO CAPITULO VII ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Juan F. del Pozo L.

ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Introducción Criterio de Nyquist La estabilidad relativa y el criterio de Nyquist Respuesta de frecuencia de circuito cerrado Estabilidad de los sistemas de control con atraso de tiempo 08/12/2017 FIEC 2

08/12/2017 FIEC 3 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Introducción Se investigará la estabilidad de un sistema en función a su respuesta a la frecuencia En base de su respuesta a la frecuencia se obtendrá información sobre su estabilidad relativa del sistema y la manera de mejorarla En 1932, Nyquist desarrolló un criterio con el que se analiza la estabilidad del sistema, tanto absoluta como relativa, a partir de su respuesta a la frecuencia

08/12/2017 FIEC 4 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Introducción En 1932, Nyquist desarrolló un criterio con el que se analiza la estabilidad del sistema, tanto absoluta como relativa, a partir de su respuesta a la frecuencia Sea F(s) la función de transferencia de un sistema El sistema es estable o no, estabilidad absoluta, en función de la ausencia o existencia de polos ubicados en el semiplano derecho del Plano Complejo En forma general:

08/12/2017 FIEC 5 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Introducción Si hacemos variar a “s” en el Plano s de tal forma que genere un recorrido cerrado “Gs” que abarque todo el semiplano derecho (“Recorrido de Nyquist”) y si F(s) tiene polos y ceros ubicados en ese semiplano, la transformación conforme de F(s) generará un contorno cerrado “GF” que encerrará el origen del Plano Complejo un número equivalente a la diferencia de ceros menos polos ubicados a la derecha del Plano s Por ejemplo: F(s) = 1/(s+p1)(s+p2)(s+p3) F(s) tiene 2 polos en el semiplano de la derecha: P = 2; y ningún cero: Z = 0; el sistema es inestable. En el Plano Complejo, el ángulo total de F(s) produce 2 circulamientos en dirección CMR, N = -2. que también ponen de manifiesto que el sistema es inestable. Para que el sistema sea estable, no debe haber polos de F(s) en el semiplano de la derecha; o dicho de otra manera, N debe ser igual a Z; en nuestro caso: P ¹ 0 y N ¹ Z; el sistema es inestable.

08/12/2017 FIEC 6 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Introducción Lo que se ha comprobado con esto es algo trivial, puesto que si sé la ubicación de las raíces de la Ecuación Característica, sabré su estabilidad absoluta. De la Ecuación Característica conozco sus polos que equivalen a los polos de lazo abierto, pero no sus ceros que corresponden a las raíces de la Ecuación Característica. Pero si ahora en lugar de hacer el análisis de q(s), Ecuación Característica, lo hacemos a H(s)G(s) que representa la “Función de Transferencia de Lazo Abierto” de la cual si conozco tanto sus ceros como sus polos, tendré: Este cambio implica que en lugar de tomar en cuenta los circulamientos del origen del plano complejo, ahora tomaremos en cuenta los circulamientos al punto (-1 j 0)

08/12/2017 FIEC 7 Criterio de Nyquist Para que un sistema sea estable, es necesario que todos los polos de la Función de Transferencia de Lazo Cerrado “T(s)” deben encontrarse en el semiplano de la izquierda del plano “s”; o dicho de otra manera los ceros (sus raíces) de la Ecuación Característica “q(s)” ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA

08/12/2017 FIEC 8 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Criterio de Nyquist Selecciono un recorrido cerrado Gs en el sentido de las manecillas del reloj que encierre todo el semiplano de la derecha La transformación conforme para GH(s) genera también un recorrido cerrado GGH en el plano complejo Se establece si el recorrido GGH encierra o no el punto (-1 j0), y si lo hace, establecer el valor de N que es el número de veces del circulamiento y su dirección, positivo si es en el sentido del reloj y negativo si CMR Puesto que conozco el número de polos P de GH(s) encerrados en Gs y el valor de N de los circulamientos del punto (-1 j0) del gráfico conforme de GH(s), puedo obtener Z que corresponderá al número de ceros (raíces) de q(s) encerrados en Gs Para que el sistema sea estable es indispensable que: “Z = 0”, o lo que es lo mismo: “N = - P”

08/12/2017 FIEC 9 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Criterio de Nyquist Aplicar el criterio de estabilidad de Nyquist a un sistema en que su función de transferencia de lazo tiene tres polos, uno en el origen, otro en –1/t1 y otro en –1/t2. . Ejemplo 9.3 Selecciono un recorrido cerrado Gs en el sentido de las manecillas del reloj que encierre todo el semiplano de la derecha Identifico los puntos: a, b, c, d, e, f, g, h Nota: observe que el recorrido Gs no pasa por encima del polo en el origen debido a que es un punto singular de GH(s) Genero la transformación conforme de esos puntos para GH(s), que serán puntos del recorrido cerrado GGH

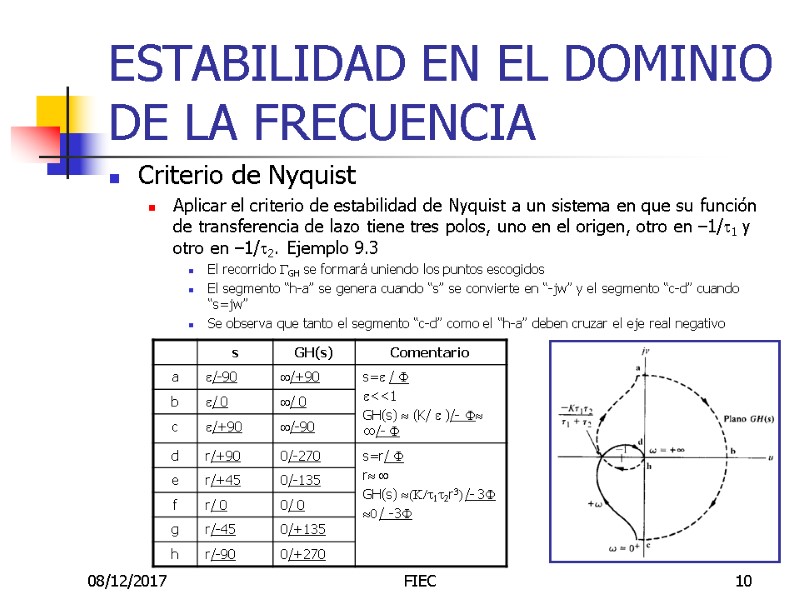
08/12/2017 FIEC 10 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Criterio de Nyquist Aplicar el criterio de estabilidad de Nyquist a un sistema en que su función de transferencia de lazo tiene tres polos, uno en el origen, otro en –1/t1 y otro en –1/t2. Ejemplo 9.3 El recorrido GGH se formará uniendo los puntos escogidos El segmento “h-a” se genera cuando “s” se convierte en “-jw” y el segmento “c-d” cuando “s=jw” Se observa que tanto el segmento “c-d” como el “h-a” deben cruzar el eje real negativo

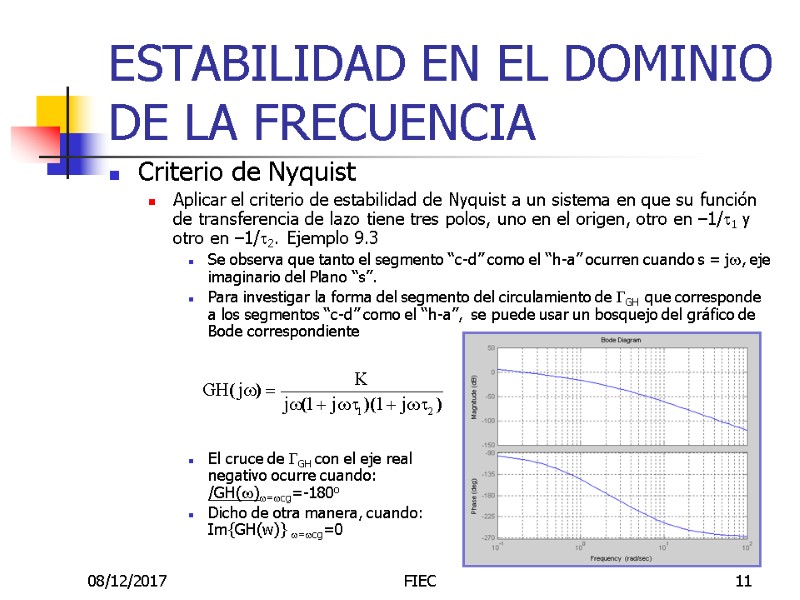
08/12/2017 FIEC 11 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Criterio de Nyquist Aplicar el criterio de estabilidad de Nyquist a un sistema en que su función de transferencia de lazo tiene tres polos, uno en el origen, otro en –1/t1 y otro en –1/t2. Ejemplo 9.3 Se observa que tanto el segmento “c-d” como el “h-a” ocurren cuando s = jw, eje imaginario del Plano “s”. Para investigar la forma del segmento del circulamiento de GGH que corresponde a los segmentos “c-d” como el “h-a”, se puede usar un bosquejo del gráfico de Bode correspondiente El cruce de GGH con el eje real negativo ocurre cuando: /GH(w)w=wcg=-180o Dicho de otra manera, cuando: Im{GH(w)} w=wcg=0

08/12/2017 FIEC 12 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Criterio de Nyquist Se observa que tanto el segmento “c-d” como el “h-a” deben cruzar el eje real negativo Para investigar en forma analítica este punto tenemos: La estabididad absoluta del sistema depende del valor de la parte real de GH(w) referente a (-1 j0)

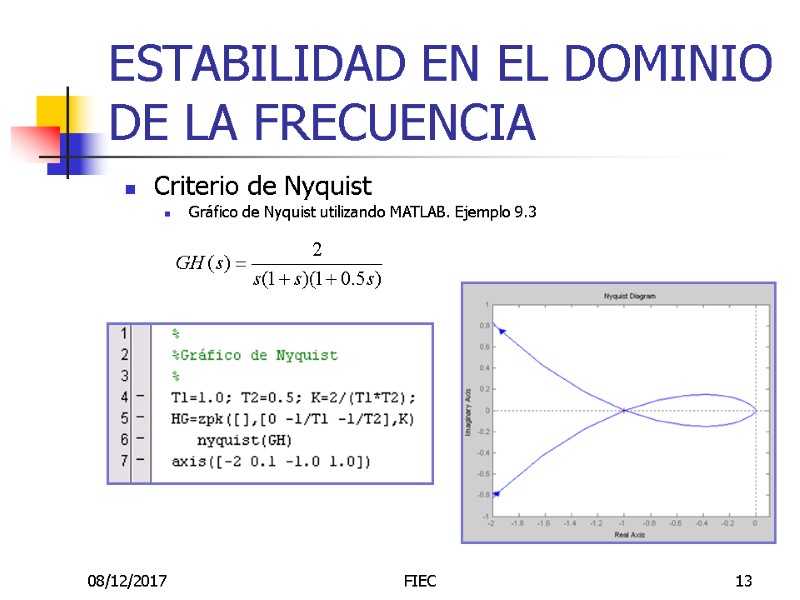
08/12/2017 FIEC 13 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Criterio de Nyquist Gráfico de Nyquist utilizando MATLAB. Ejemplo 9.3

08/12/2017 FIEC 14 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Criterio de Nyquist Aplicar el criterio de estabilidad de Nyquist a un sistema que posee un cero en el semiplano de la derecha y dos polos iguales en el semiplano de la izquierda. Ejercicio 9.6 Selecciono un recorrido cerrado Gs en el sentido de las manecillas del reloj que encierre todo el semiplano de la derecha Identifico los puntos: a, b, c, d, e, f Genero la transformación conforme de esos puntos para GH(s), que serán puntos del recorrido cerrado GGH El segmento “a-b” se genera cuando “s” se convierte en “+jw” y el segmento “f-a” cuando “s=-jw”

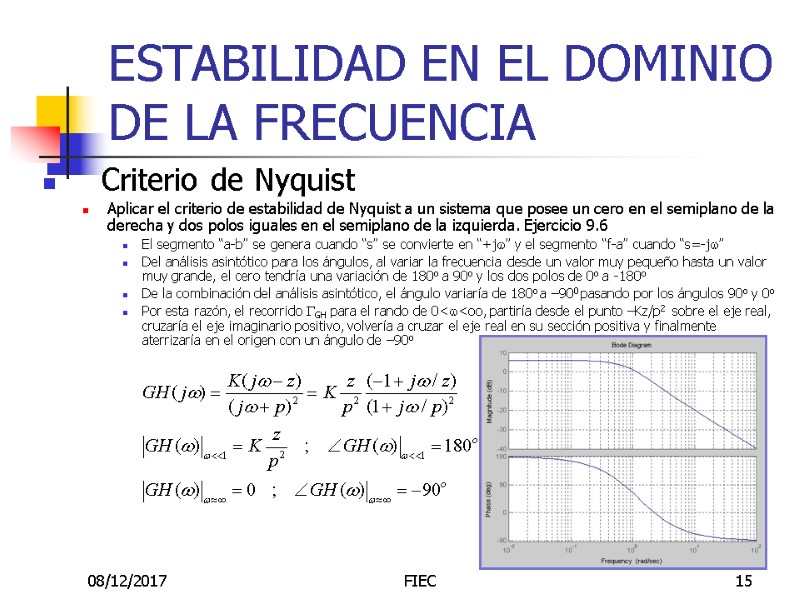
08/12/2017 FIEC 15 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Criterio de Nyquist Aplicar el criterio de estabilidad de Nyquist a un sistema que posee un cero en el semiplano de la derecha y dos polos iguales en el semiplano de la izquierda. Ejercicio 9.6 El segmento “a-b” se genera cuando “s” se convierte en “+jw” y el segmento “f-a” cuando “s=-jw” Del análisis asintótico para los ángulos, al variar la frecuencia desde un valor muy pequeño hasta un valor muy grande, el cero tendría una variación de 180o a 90o y los dos polos de 0o a -180o De la combinación del análisis asintótico, el ángulo variaría de 180o a –900 pasando por los ángulos 90o y 0o Por esta razón, el recorrido GGH para el rando de 0

08/12/2017 FIEC 16 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Criterio de Nyquist Aplicar el criterio de estabilidad de Nyquist a un sistema que posee un cero en el semiplano de la derecha y dos polos iguales en el semiplano de la izquierda. Ejercicio 9.6 Diagrama de Nyquist utilizando MATLAB, para valores de K=0.4(azul), 0.5(verde), 0.6(rojo) Situación: estable (N=0, Z=0), crítica, inestable (N=1, Z=1); P=0

08/12/2017 FIEC 17 La estabilidad relativa y el criterio de Nyquist El criterio de Nyquist proporciona una información adecuada relacionada con la estabilidad absoluta Nyquist define la estabilidad absoluta en términos de los circulamientos al punto (-1 j0) del plano complejo La proximidad del gráfico polar de GH(jw) al punto (-1 j0) es una medida de la estabilidad relativa del sistema La ganancia del sistema produce alteraciones al gráfico polar de GH(jw), de tal manera de alejarse o acercarse al punto (-1 j0), introduciendo el criterio de un mejor o peor margen para la estabilidad; es decir, una idea de estabilidad relativa Dada la dominancia de los sistemas de segundo orden, se establecerá una relación entre la respuesta a la frecuencia y su comportamiento dinámico en el dominio del tiempo ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA

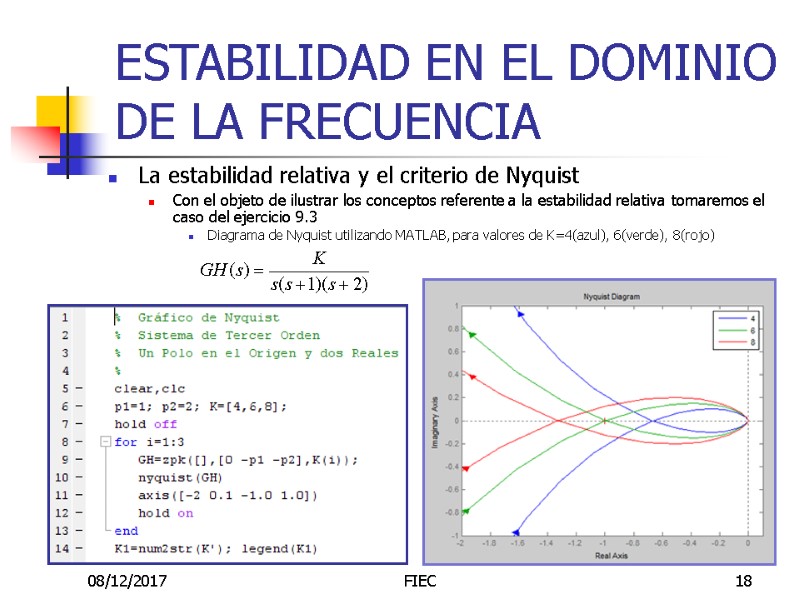
08/12/2017 FIEC 18 La estabilidad relativa y el criterio de Nyquist Con el objeto de ilustrar los conceptos referente a la estabilidad relativa tomaremos el caso del ejercicio 9.3 Diagrama de Nyquist utilizando MATLAB, para valores de K=4(azul), 6(verde), 8(rojo) ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA

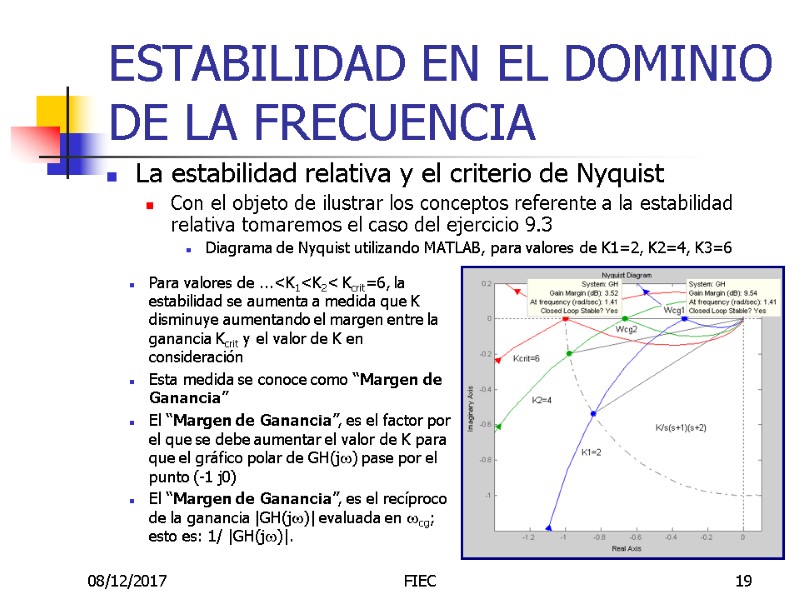
08/12/2017 FIEC 19 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA La estabilidad relativa y el criterio de Nyquist Con el objeto de ilustrar los conceptos referente a la estabilidad relativa tomaremos el caso del ejercicio 9.3 Diagrama de Nyquist utilizando MATLAB, para valores de K1=2, K2=4, K3=6 Para valores de ...

08/12/2017 FIEC 20 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA La estabilidad relativa y el criterio de Nyquist Con el objeto de ilustrar los conceptos referente a la estabilidad relativa tomaremos el caso del ejercicio 9.3 Diagrama de Nyquist utilizando MATLAB, para valores de K1=2, K2=4, K3=6 Una medida alterna de la estabilidad relativa puede definirse en términos del margen del ángulo de fase entre el sistema actual y su caso marginalmente estable Esta medida se conoce como “Margen de Fase” El “Margen de Fase”, es el ángulo de fase a través del cual debe girar el gráfico polar de GH(jw) , en “wcp”, para que pase por el punto (-1 j0) El “Margen de Fase”, es igual a la fase adicional que se necesita antes de que el sistema se vuelva inestable

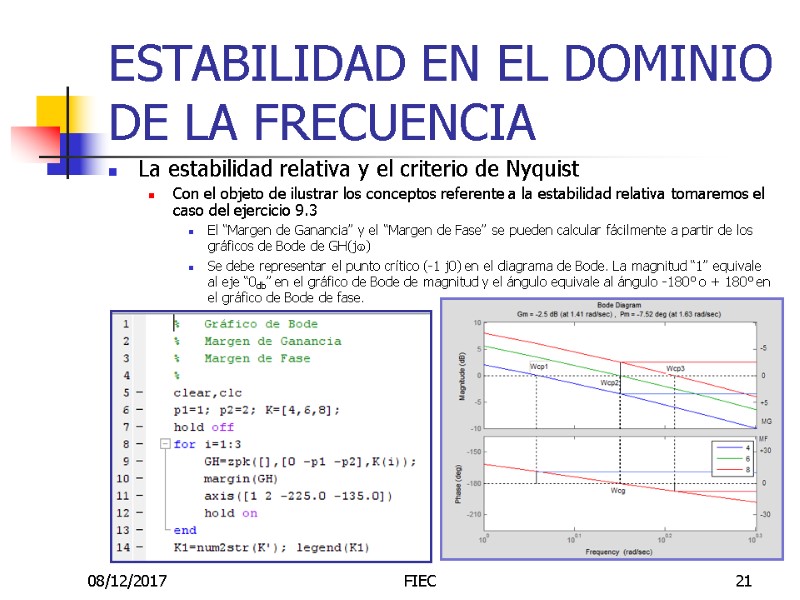
08/12/2017 FIEC 21 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA La estabilidad relativa y el criterio de Nyquist Con el objeto de ilustrar los conceptos referente a la estabilidad relativa tomaremos el caso del ejercicio 9.3 El “Margen de Ganancia” y el “Margen de Fase” se pueden calcular fácilmente a partir de los gráficos de Bode de GH(jw) Se debe representar el punto crítico (-1 j0) en el diagrama de Bode. La magnitud “1” equivale al eje “0db” en el gráfico de Bode de magnitud y el ángulo equivale al ángulo -180° o + 180° en el gráfico de Bode de fase.

08/12/2017 FIEC 22 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Margen de fase de un sistema de segundo orden Dada la gran importancia de los sistemas de segundo orden (puesto que muchos sistemas pueden ser aproximados a uno de este tipo), se establecerá una relación entre la respuesta a la frecuencia y su comportamiento dinámico en el dominio del tiempo Se encontrará una vinculación entre el Margen de Fase y la Constante de Amortiguamiento La función de transferencia de lazo GH(jw) para un sistema de segundo grado es: La expresión correspondiente a la fase y magnitud:

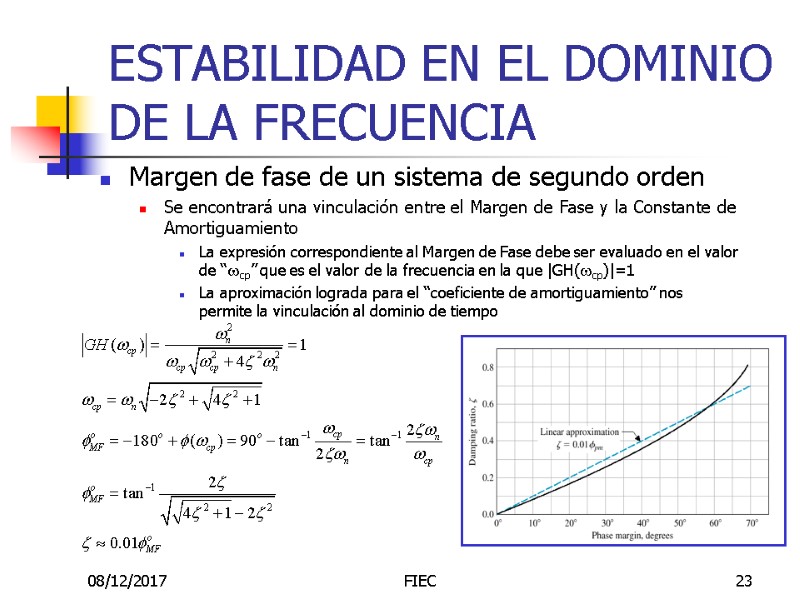
08/12/2017 FIEC 23 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Margen de fase de un sistema de segundo orden Se encontrará una vinculación entre el Margen de Fase y la Constante de Amortiguamiento La expresión correspondiente al Margen de Fase debe ser evaluado en el valor de “wcp” que es el valor de la frecuencia en la que |GH(wcp)|=1 La aproximación lograda para el “coeficiente de amortiguamiento” nos permite la vinculación al dominio de tiempo

08/12/2017 FIEC 24 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Respuesta de frecuencia de circuito cerrado Ancho de Banda del sistema El Ancho de Banda de un sistema de realimentación de lazo cerrado nos proporciona una excelente medida de la fidelidad de su respuesta En sistemas de lazo cerrado, en los que la magnitud para bajas frecuencias asintóticamente es 0 db, el Ancho de Banda es la frecuencia “wBP” en donde la curva de la magnitud es –3 db La velocidad de respusta de un sistema de lazo cerrado será proporcional a “wBP” El tiempo de estabilización “Ts” de un sistema de lazo cerrado es inversamente proporcional a “wBP”

08/12/2017 FIEC 25 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Respuesta de frecuencia de circuito cerrado Ancho de Banda del sistema Sección 9.6. Consideraremos dos sistemas de lazo cerrado de segundo orden que tienen igual coeficiente de amortiguamiento. Observaremos sus respuestas al escalón unitario

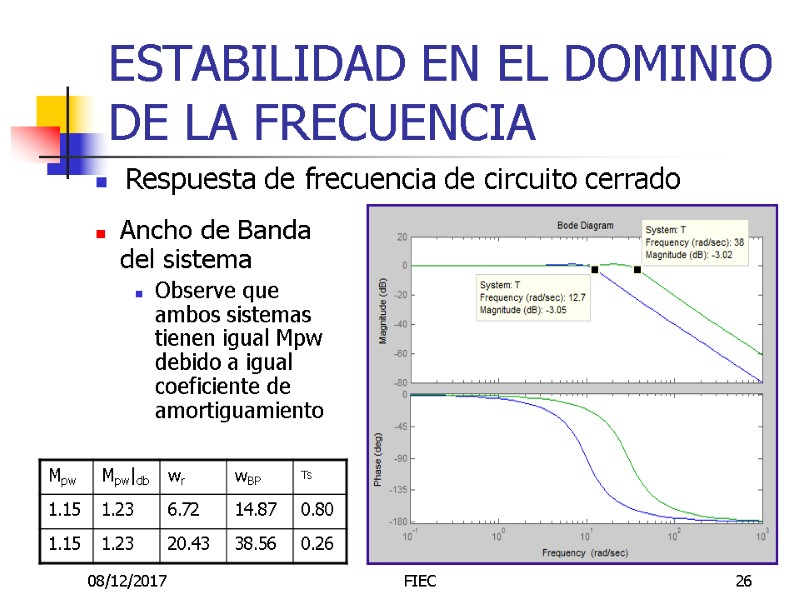
08/12/2017 FIEC 26 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Ancho de Banda del sistema Observe que ambos sistemas tienen igual Mpw debido a igual coeficiente de amortiguamiento Respuesta de frecuencia de circuito cerrado

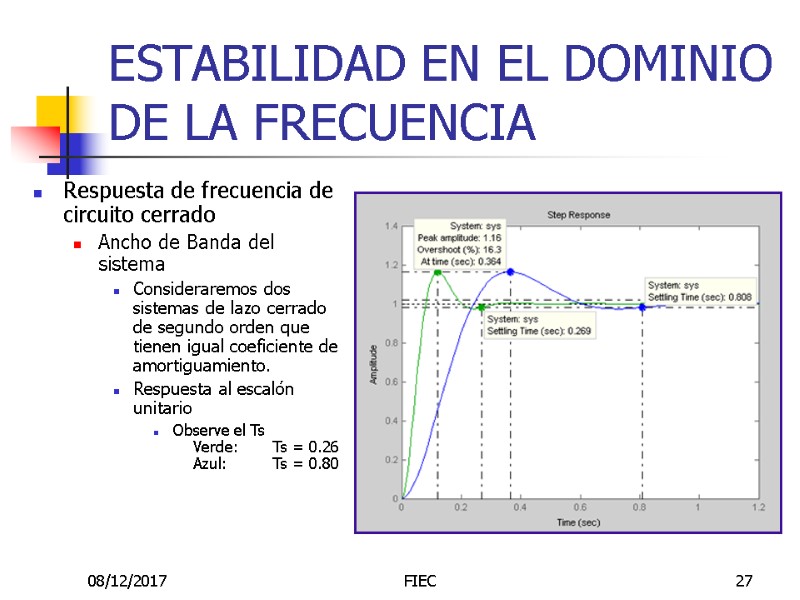
08/12/2017 FIEC 27 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Respuesta de frecuencia de circuito cerrado Ancho de Banda del sistema Consideraremos dos sistemas de lazo cerrado de segundo orden que tienen igual coeficiente de amortiguamiento. Respuesta al escalón unitario Observe el Ts Verde: Ts = 0.26 Azul: Ts = 0.80

08/12/2017 FIEC 28 Estabilidad de los sistemas de control con atraso de tiempo Existen muchos sistemas de control que tienen un atraso de tiempo dentro del circuito cerrado Se presenta en aquellos sistemas en donde se mueve un material que necesita un tiempo finito para pasar de un punto a otro El atraso de tiempo afecta a la estabilidad del sistema El efecto del atraso de tiempo es conveniente visualizarlo con el método de Nyquist debido a que no afecta a la curva de la magnitud solo altera la curva de la fase ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA

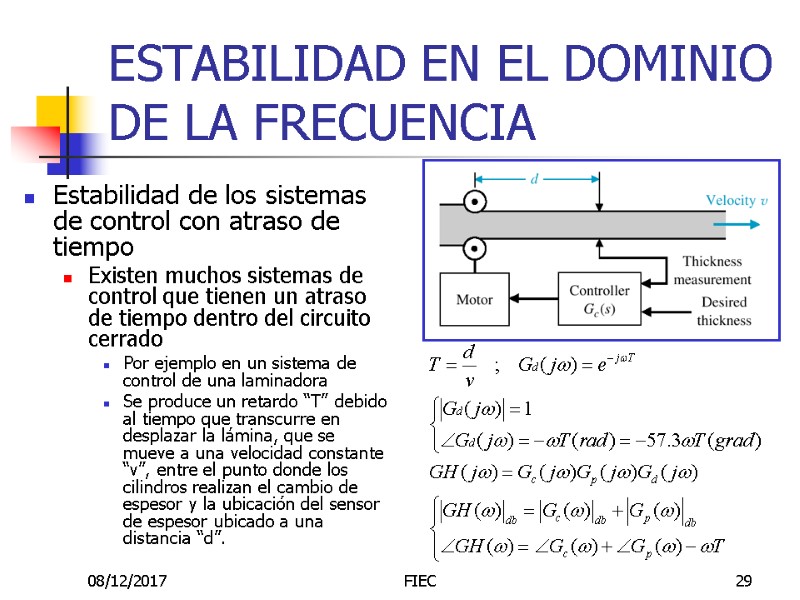
08/12/2017 FIEC 29 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Estabilidad de los sistemas de control con atraso de tiempo Existen muchos sistemas de control que tienen un atraso de tiempo dentro del circuito cerrado Por ejemplo en un sistema de control de una laminadora Se produce un retardo “T” debido al tiempo que transcurre en desplazar la lámina, que se mueve a una velocidad constante “v”, entre el punto donde los cilindros realizan el cambio de espesor y la ubicación del sensor de espesor ubicado a una distancia “d”.

ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Estabilidad de los sistemas de control con atraso de tiempo Existen muchos sistemas de control que tienen un atraso de tiempo dentro del circuito cerrado Por ejemplo en un sistema de control de una laminadora Se produce un retardo “T” debido al tiempo que transcurre en desplazar la lámina, que se mueve a una velocidad constante “v”, entre el punto donde los cilindros realizan el cambio de espesor y la ubicación del sensor de espesor ubicado a una distancia “d”. 08/12/2017 FIEC 30

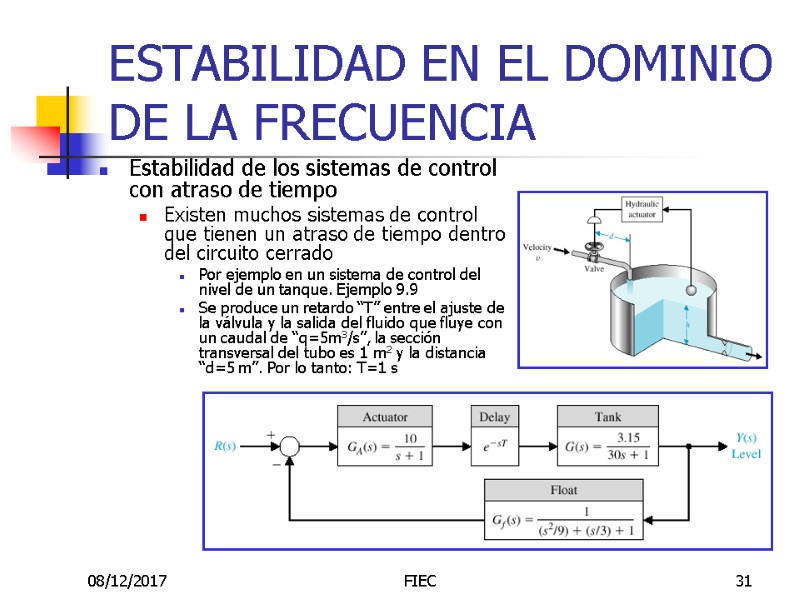
08/12/2017 FIEC 31 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Estabilidad de los sistemas de control con atraso de tiempo Existen muchos sistemas de control que tienen un atraso de tiempo dentro del circuito cerrado Por ejemplo en un sistema de control del nivel de un tanque. Ejemplo 9.9 Se produce un retardo “T” entre el ajuste de la válvula y la salida del fluido que fluye con un caudal de “q=5m3/s”, la sección transversal del tubo es 1 m2 y la distancia “d=5 m”. Por lo tanto: T=1 s

08/12/2017 FIEC 32 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Estabilidad de los sistemas de control con atraso de tiempo Existen muchos sistemas de control que tienen un atraso de tiempo dentro del circuito cerrado Por ejemplo en un sistema de control del nivel de un tanque. Ejemplo 9.9a Se produce un retardo “T” entre el ajuste de la válvula y la salida del fluido que fluye con un caudal de “q=5m3/s”, la sección transversal del tubo es 1 m2 y la distancia “d=5 m”. Por lo tanto: T=1 s

08/12/2017 FIEC 33 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Estabilidad de los sistemas de control con atraso de tiempo Existen muchos sistemas de control que tienen un atraso de tiempo dentro del circuito cerrado Por ejemplo en un sistema de control del nivel de un tanque. Ejemplo 9.9 Se produce un retardo “T” entre el ajuste de la válvula y la salida del fluido que fluye con un caudal de “q=5 m3/s”, la sección transversal del tubo es 1 m2 y la distancia “d=5 m”. Por lo tanto: T=1 s Para efecto de cálculo, el retardo lo representaremos mediante la Función de “Pade”. En nuestro caso usaremos la aproximación de segundo orden

08/12/2017 FIEC 34 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Estabilidad de los sistemas de control con atraso de tiempo Sistema de control del nivel de un tanque. Ajustar K de tal forma que el MF = 30º Ejemplo 9.9b

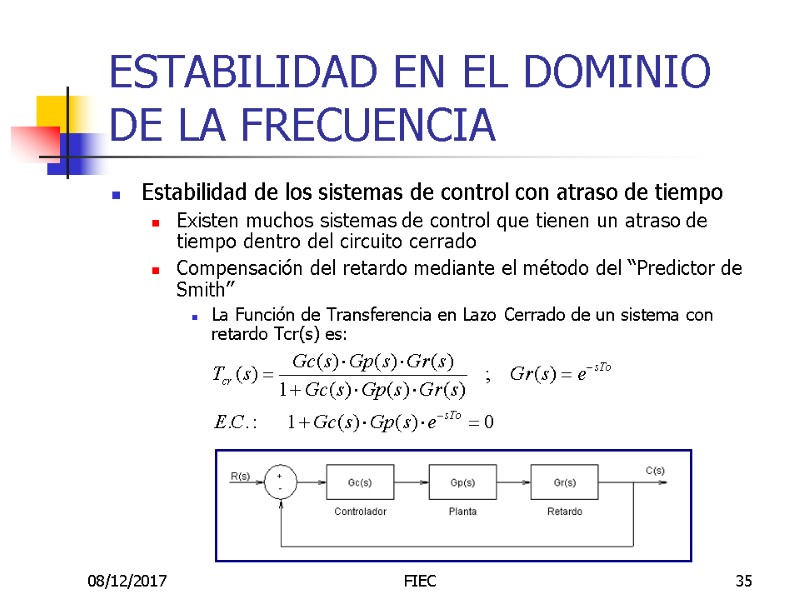
08/12/2017 FIEC 35 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Estabilidad de los sistemas de control con atraso de tiempo Existen muchos sistemas de control que tienen un atraso de tiempo dentro del circuito cerrado Compensación del retardo mediante el método del “Predictor de Smith” La Función de Transferencia en Lazo Cerrado de un sistema con retardo Tcr(s) es:

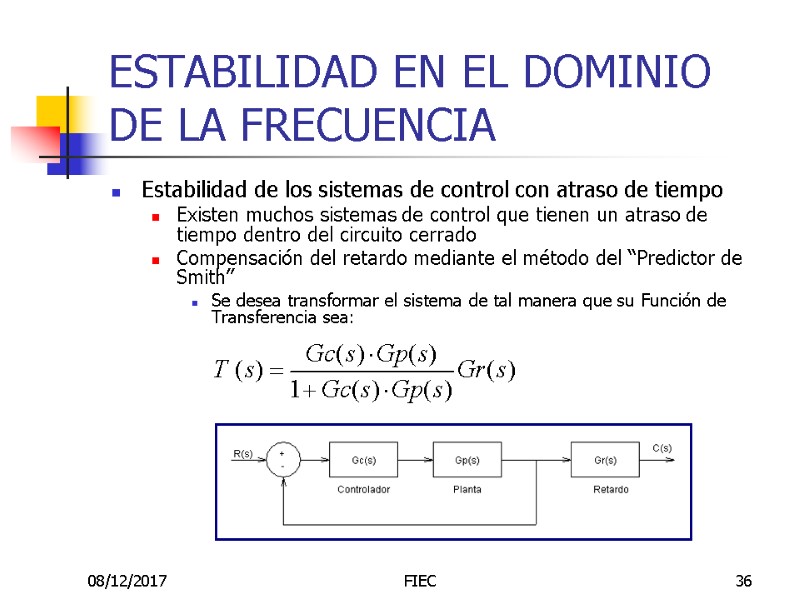
08/12/2017 FIEC 36 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Estabilidad de los sistemas de control con atraso de tiempo Existen muchos sistemas de control que tienen un atraso de tiempo dentro del circuito cerrado Compensación del retardo mediante el método del “Predictor de Smith” Se desea transformar el sistema de tal manera que su Función de Transferencia sea:

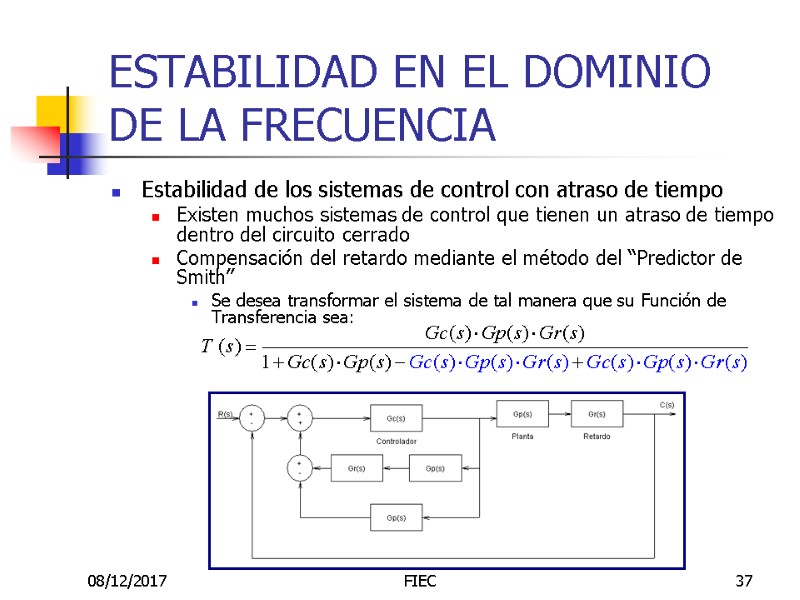
08/12/2017 FIEC 37 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Estabilidad de los sistemas de control con atraso de tiempo Existen muchos sistemas de control que tienen un atraso de tiempo dentro del circuito cerrado Compensación del retardo mediante el método del “Predictor de Smith” Se desea transformar el sistema de tal manera que su Función de Transferencia sea:

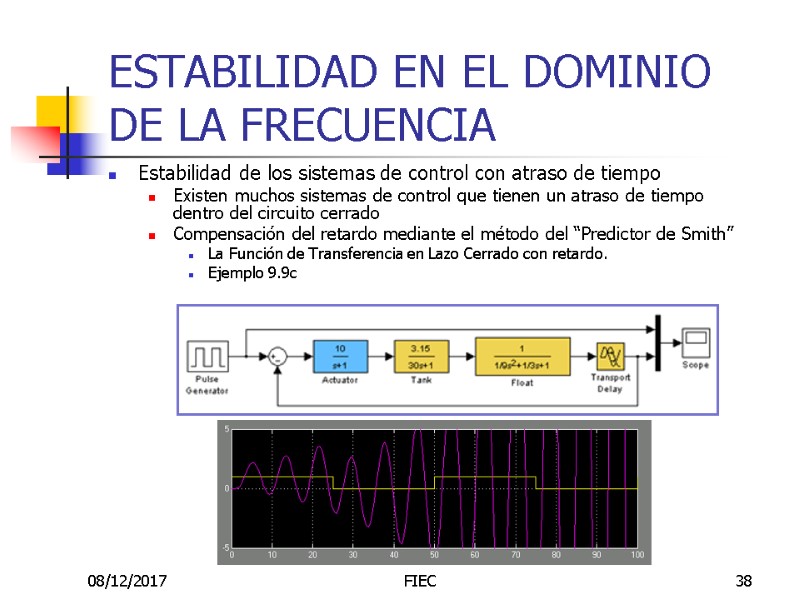
08/12/2017 FIEC 38 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Estabilidad de los sistemas de control con atraso de tiempo Existen muchos sistemas de control que tienen un atraso de tiempo dentro del circuito cerrado Compensación del retardo mediante el método del “Predictor de Smith” La Función de Transferencia en Lazo Cerrado con retardo. Ejemplo 9.9c

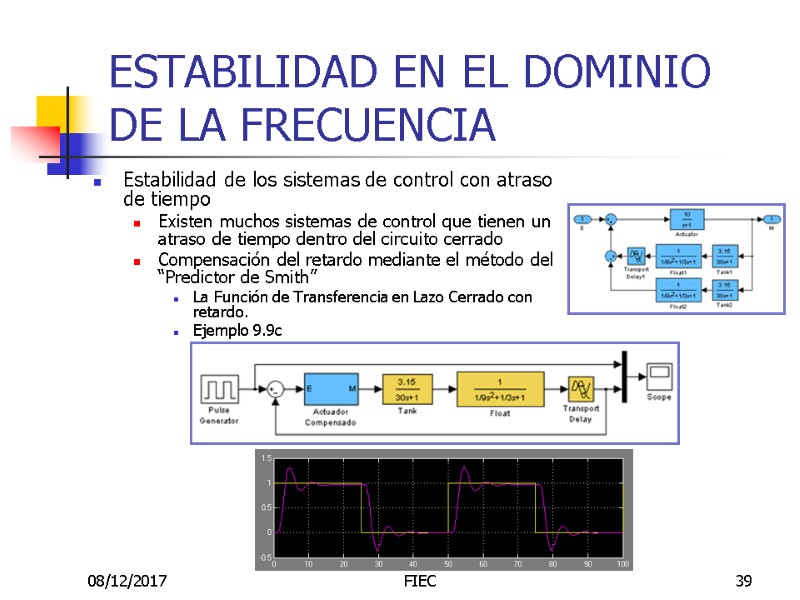
08/12/2017 FIEC 39 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Estabilidad de los sistemas de control con atraso de tiempo Existen muchos sistemas de control que tienen un atraso de tiempo dentro del circuito cerrado Compensación del retardo mediante el método del “Predictor de Smith” La Función de Transferencia en Lazo Cerrado con retardo. Ejemplo 9.9c

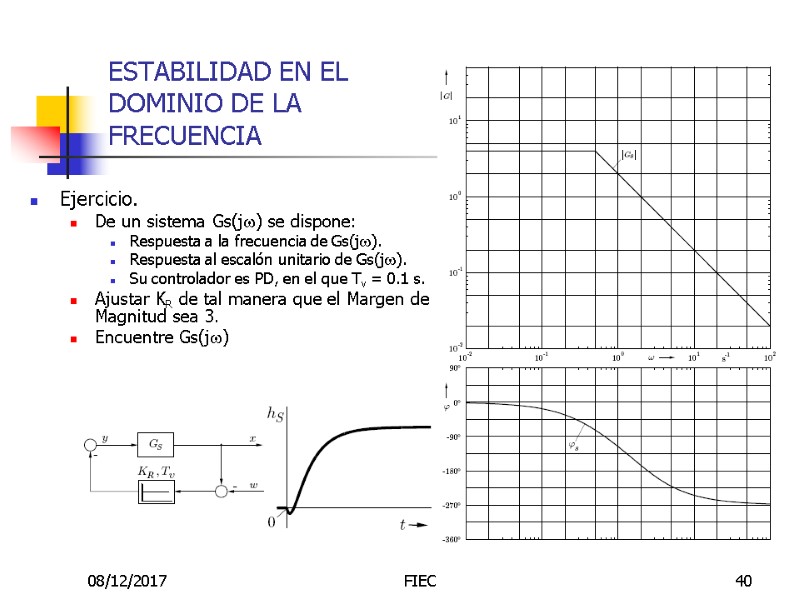
08/12/2017 FIEC 40 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Ejercicio. De un sistema Gs(jw) se dispone: Respuesta a la frecuencia de Gs(jw). Respuesta al escalón unitario de Gs(jw). Su controlador es PD, en el que Tv = 0.1 s. Ajustar KR de tal manera que el Margen de Magnitud sea 3. Encuentre Gs(jw)

08/12/2017 FIEC 41 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Ejercicio. Del gráfico de de Bode de magnitud de Gs(jw) se puede reconocer que se trata de un sistema de “Primer Orden”. Del gráfico de respuesta al escalón se observa que el sistema tiene retardo. Del gráfico de fase de Gs(jw), para frecuencias muy altas, el ángulo es asintótico a -270º; por lo tanto, según Pade, el retardo debe ser de primer orden puesto que contribuye con - 180º. El retardo contribuirá en w = 2/T con - 90º al gráfico del ángulo del sistema de primer orden.

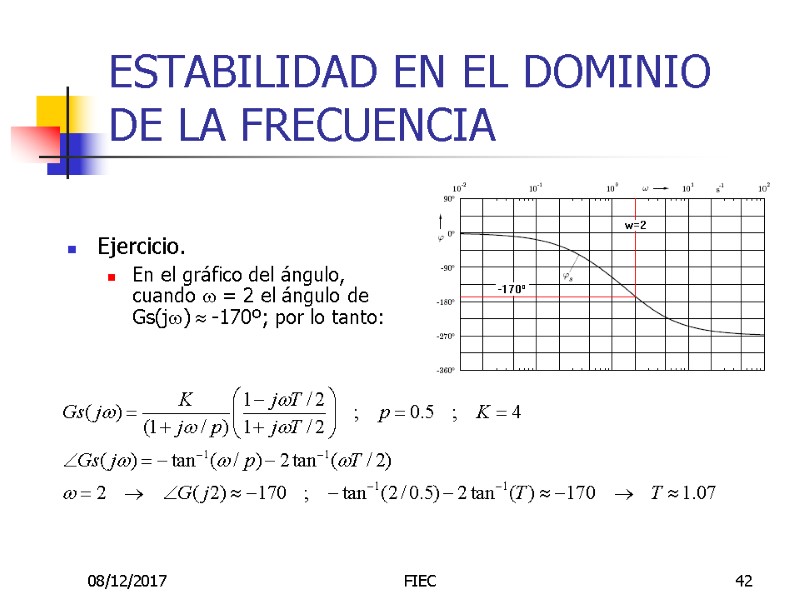
08/12/2017 FIEC 42 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Ejercicio. En el gráfico del ángulo, cuando w = 2 el ángulo de Gs(jw) » -170º; por lo tanto:

08/12/2017 FIEC 43 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Ejercicio. El controlador es PD, en el que Tv = 0.1 s. Ajustar KR de tal manera que el Margen de Magnitud sea 3. El ángulo de de la Función de Transferencia de Lazo Abierto debe ser -180º cuando la frecuencia es wcg, en ese valor de la frecuencia se deberá evaluar el Margen de Ganancia deseado. Utilizando Matlab se puede encontrar el valor de la frecuencia wcg >> w=solve('atan(0.1*w)-atan(2*w)-2*atan(0.535*w)+pi','w') w = 3.00078

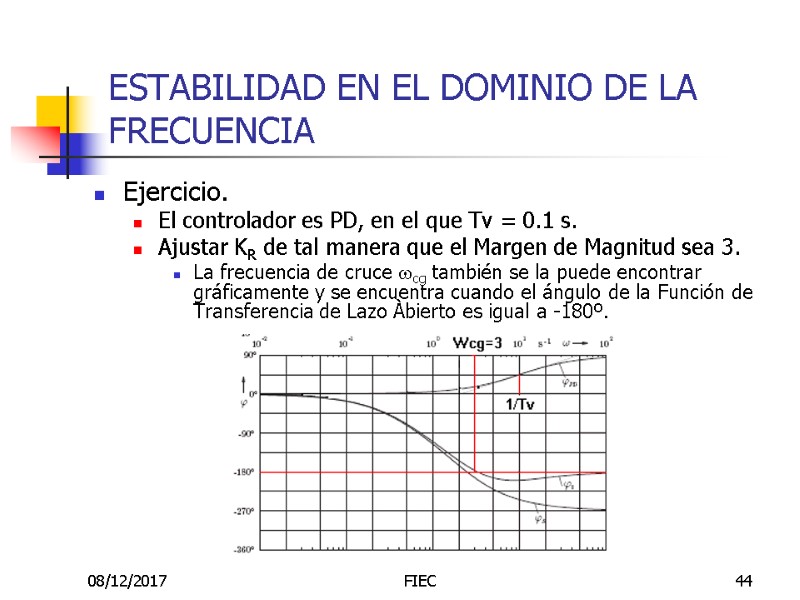
08/12/2017 FIEC 44 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Ejercicio. El controlador es PD, en el que Tv = 0.1 s. Ajustar KR de tal manera que el Margen de Magnitud sea 3. La frecuencia de cruce wcg también se la puede encontrar gráficamente y se encuentra cuando el ángulo de la Función de Transferencia de Lazo Àbierto es igual a -180º.

08/12/2017 FIEC 45 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Ejercicio. El controlador es PD, en el que Tv = 0.1 s. Ajustar KR de tal manera que el Margen de Magnitud sea 3. La Magnitud de Lazo Abierto evaluado en la frecuencia de cruce wcg es igual al inverso del Margen de Magnitud.

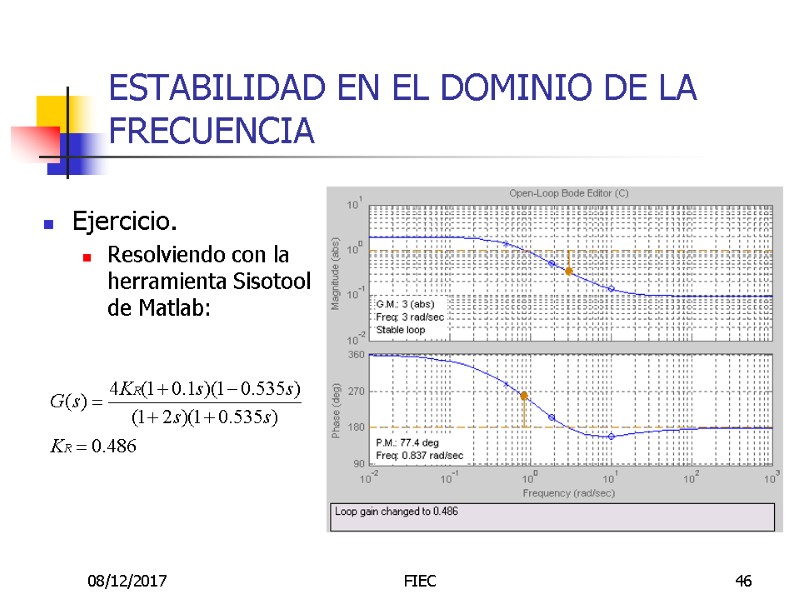
08/12/2017 FIEC 46 ESTABILIDAD EN EL DOMINIO DE LA FRECUENCIA Ejercicio. Resolviendo con la herramienta Sisotool de Matlab: