Contingency analysis Sample Test statistic Null hypothesis

Contingency analysis

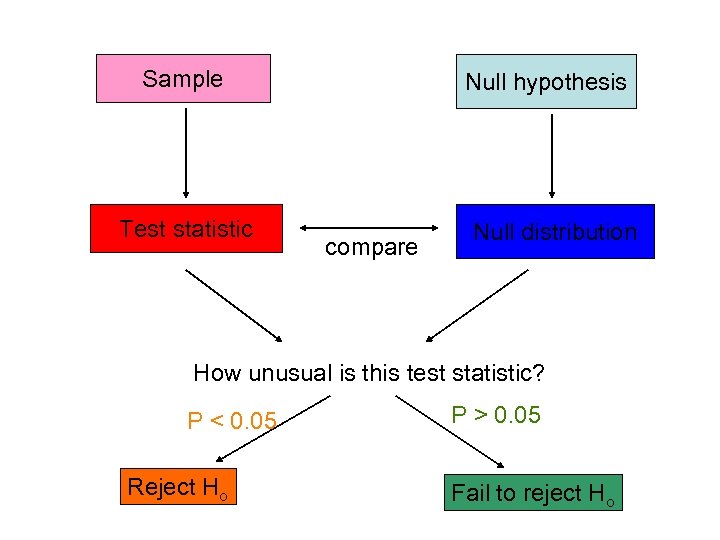Sample Test statistic Null hypothesis compare Null distribution How unusual is this test statistic? P < 0. 05 Reject Ho P > 0. 05 Fail to reject Ho

Using one tail in the 2 • We always use only one tail for a 2 test • Why?

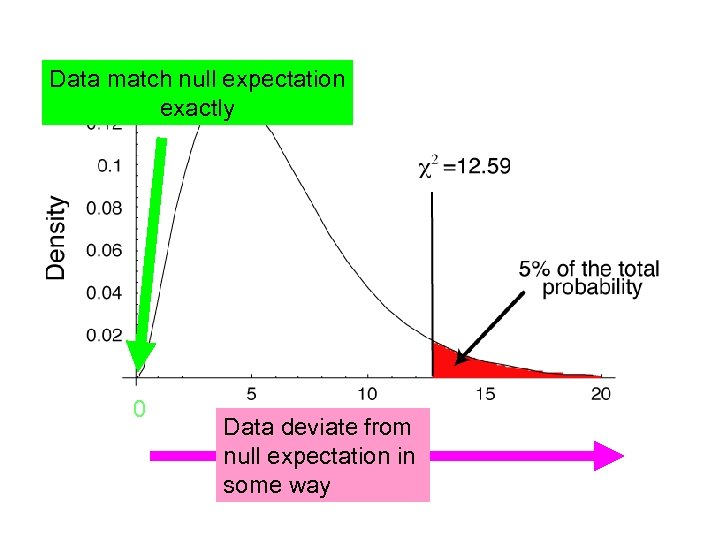Data match null expectation exactly 0 Data deviate from null expectation in some way

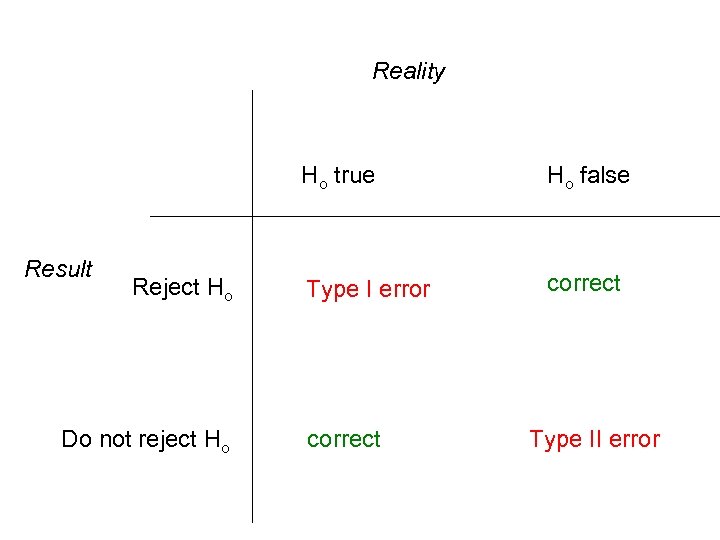Reality Ho true Result Reject Ho Do not reject Ho Ho false Type I error correct Type II error

If null hypothesis is really true… Do not reject Ho Correct answer Reject Ho Type I error Test statistic

If null hypothesis is really false… Do not reject Ho Type II error Reject Ho correct Test statistic

Errors and statistics • These are theoretical - you usually don’t know for sure if you’ve made an error • Pr[Type I error] = • Pr[Type II error] = … – Requires power analysis – Depends on sample size

Contingency analysis • Estimates and tests for an association between two or more categorical variables

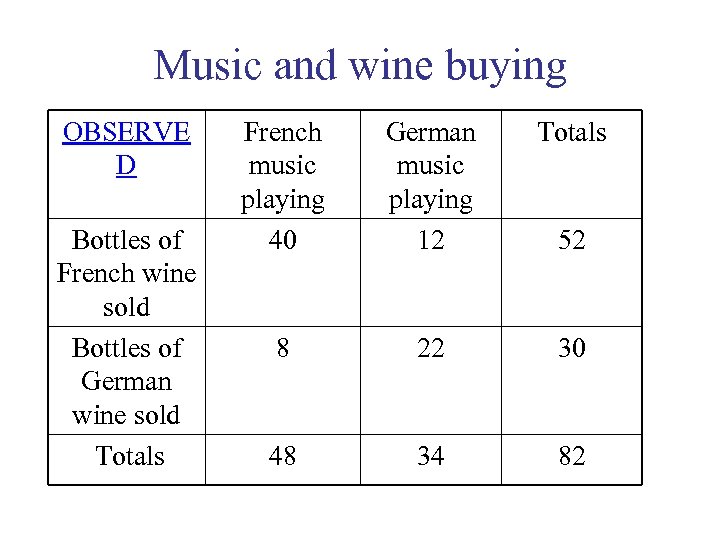Music and wine buying OBSERVE D Bottles of French wine sold Bottles of German wine sold Totals French music playing 40 German music playing 12 Totals 8 22 30 48 34 82 52

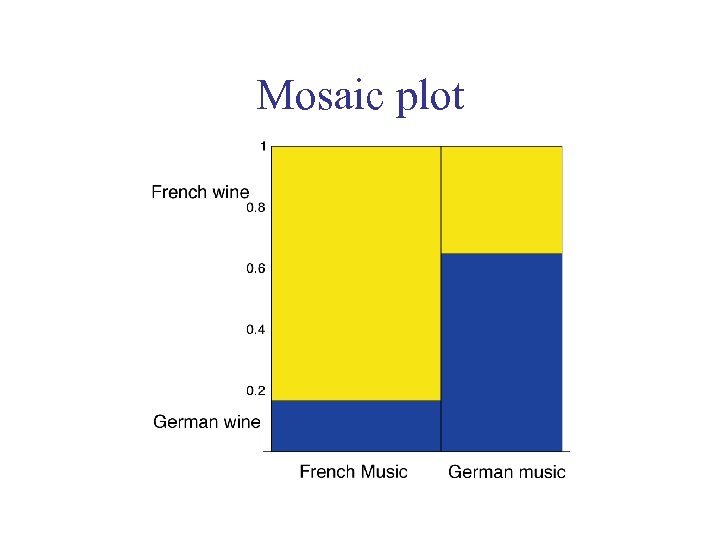Mosaic plot

Odds ratio • Odds of success = probability of success divided by the probability of failure

Estimating the Odds ratio • Odds of success = probability of success divided by the probability of failure

Music and wine buying OBSERVED French music playing Bottles of French wine sold Bottles of German wine sold Totals 40 8 48

Example • Out of 48 bottles of wine, 40 were French

Example • Out of 48 bottles of wine, 40 were French Interpretation: people are about 5 times more likely to buy a French wine

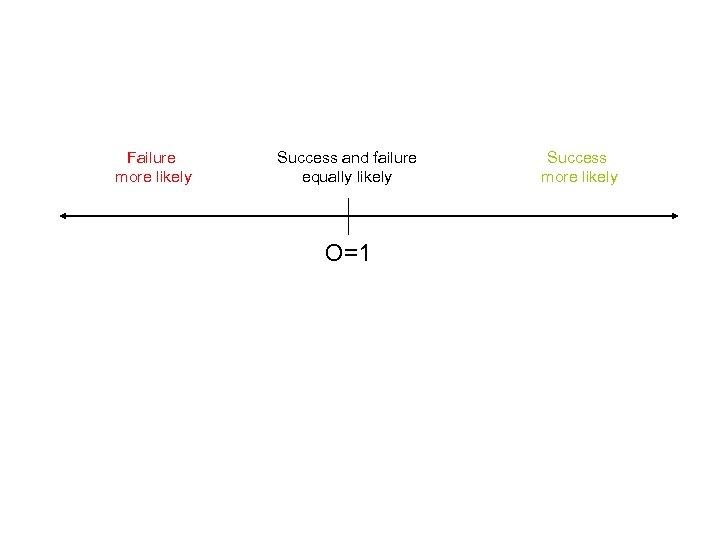Failure more likely Success and failure equally likely O=1 Success more likely

Odds ratio • The odds of success in one group divided by the odds of success in a second group

Estimating the Odds ratio • The odds of success in one group divided by the odds of success in a second group

Music and wine buying • Group 1 = French music, Group 2 = German music • Success = French wine

Group 2 • Out of 34 bottles of wine, 12 were French

Music and wine buying • Group 1 = French music, Group 2 = German music • Success = French wine

Music and wine buying • Group 1 = French music, Group 2 = German music • Success = French wine Interpretation: people are about 9 times more likely to buy French wine in Group 1 compared to Group 2

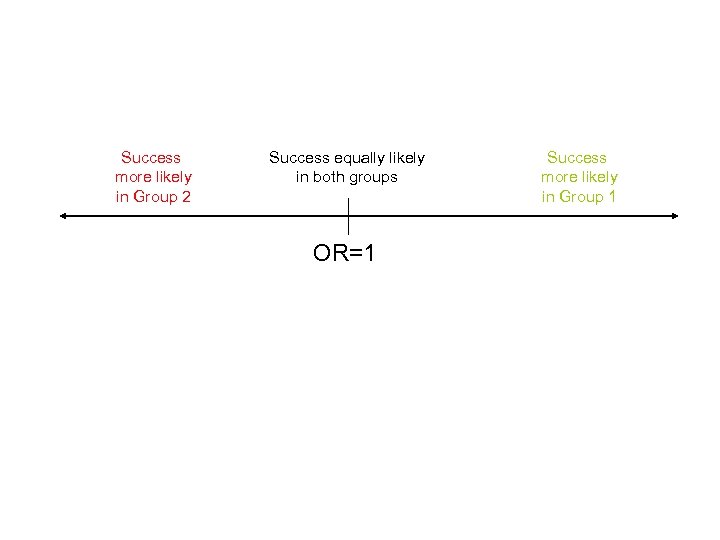Success more likely in Group 2 Success equally likely in both groups OR=1 Success more likely in Group 1

Hypothesis testing • Contingency analysis • Is there a difference in odds between two groups?

Hypothesis testing • Contingency analysis • Is there an association between two categorical variables?

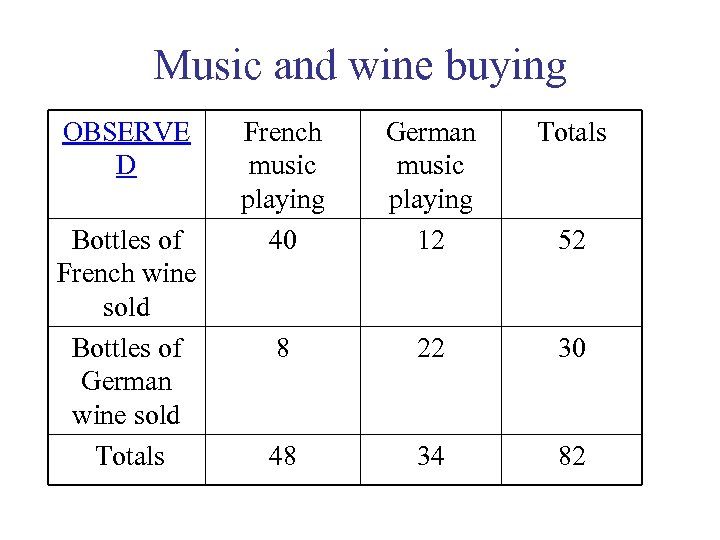Music and wine buying OBSERVE D Bottles of French wine sold Bottles of German wine sold Totals French music playing 40 German music playing 12 Totals 8 22 30 48 34 82 52

Contingency analysis • Is there a difference in the odds of buying French wine depending on the music that is playing? • Is there an association between wine bought and music playing? • Is the nationality of the wine independent of the music playing when it is sold?

Hypotheses • H 0: The nationality of the bottle of wine is independent of the nationality of the music played when it is sold. • HA: The nationality of the bottle of wine sold depends on the nationality of the music being played when it is sold.

Calculating the expectations With independence, Pr[ French wine AND French music] = Pr[French wine] Pr[French music]

Calculating the expectations OBS. French music German music Totals Pr[French wine] = 52/82=0. 634 Pr[French music] = 48/82= 0. 585 French wine sold 52 German wine sold 30 Totals 48 34 82 By H 0, Pr[French wine AND French music] = (0. 634)(0. 585)=0. 37112

Calculating the expectations EXP. French music French wine sold German music 0. 37 (82) = 30. 4 52 German wine sold Totals 30 48 34 82 By H 0, Pr[French wine AND French music] = (0. 634)(0. 585)=0. 37112

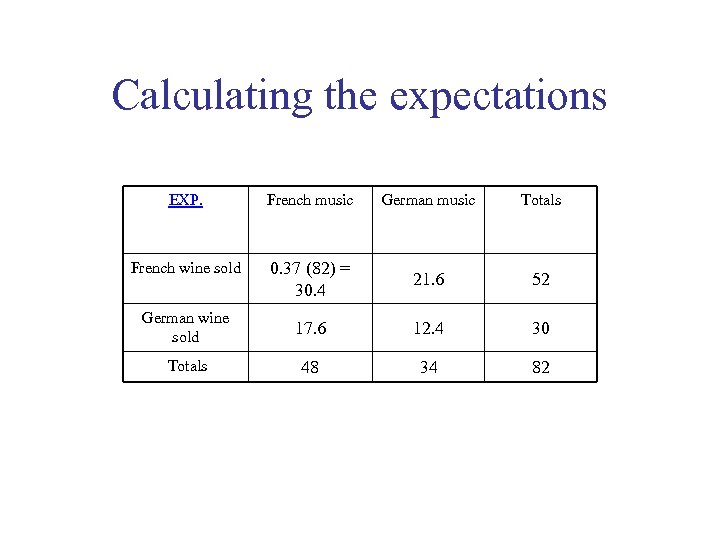Calculating the expectations EXP. French music German music Totals French wine sold 0. 37 (82) = 30. 4 21. 6 52 German wine sold 17. 6 12. 4 30 Totals 48 34 82

2

Degrees of freedom For a 2 Contingency test, df = # categories -1 - # parameters df= (# columns -1)(# rows -1) For music/wine example, df = (2 -1) = 1

Conclusion 2 = 20. 0 >> 21, =0. 05 = 3. 84, So we can reject the null hypothesis of independence, and say that the nationality of the wine sold did depend on what music was played.

Assumptions • This 2 test is just a special case of the 2 goodness-of-fit test, so the same rules apply. • You can’t have any expectation less than 1, and no more than 20% < 5

Fisher’s exact test • For 2 x 2 contingency analysis • Does not make assumptions about the size of expectations • JMP will do it, but cumbersome to do by hand

Other extensions you might see • Yates correction for continuity • G-test • Read about these in your book