Constructing Fair-Exchange Protocols for E-commerce Via Distributed Computation

Constructing Fair-Exchange Protocols for E-commerce Via Distributed Computation of RSA Signatures Jung Min Park, Edwin K. P. Chong, Howard Jay Siegel 22 -th Annual ACM Symp. on Principles of Distributed Computing, July 2003.

Outline Introduction ¢ Related Work ¢ Technical Background ¢ The Fair-exchange Protocol ¢ Efficiency Evaluations ¢ Conclusion ¢

INTRODUCTION ¢ fair-exchange problem l ¢ fair-exchange protocol l ¢ either each party gets the other's item, or neither party does Require zero-knowledge proofs in exchange protocol Novel method for constructing efficient fairexchange protocol l Employ RSA-based multisignatures No zero-knowledge proofs in exchange protocol and only once in setup phase(one-time cost) compatible with the underlying standard (singlesigner) signature scheme

INTRODUCTION-fair-exchange protocol ¢ gradual exchange protocols l l ¢ protocols requiring an online trusted third party (TTP) l l l ¢ probability of fair exchange is gradually increased over rounds Impractical: communication intensive, require equal computational power to ensure the security TTP must be available for the entire duration of every exchange protocol is simple and efficient on-line TTP is expensive, can become bottleneck optimistic fair-exchange protocols (with an offline TTP) l l TTP is involved only if one party behaves unfairly or aborts the protocol prematurely, otherwise never involved. Seem to be most practical

INTRODUCTION-optimistic fair-exchange protocol ¢ two types of protocol frameworks l ¢ Asokan et al, Bao et al cryptographic primitive each protocol employs a different technique for constructing it l ensures fairness(Fairness primitive) l is the cornerstone of the fair-exchange protocol l its design poses the greatest technical challenge. l

optimistic fair-exchange protocol framework example EXCHANGE ¢ 1. 2. Alice --- c. A, V --> Bob Alice <--- σB ----- Bob • 3. 4. Or Bob stop the protocol Alice ---- σA ----> Bob • Or Alice stop the protocol Initiate by Bob • If σA is invalid(4) or Bob do not receive σA(3) 1. Bob --- c. A, V, σB --> Charlie • l or initiates the dispute resolution protocol DISPUTE RESOLUTION 1. l End by Bob • ¢ l Charlie compute σA 1. Bob <---- σA ---- Charlie 2. Alice <---- σB ---- Charlie Alice and Bob : two players exchanging digital signatures σA and σB on a message M Charlie : TTP Fairness primitive • c. A : commitment that Alice send to Bob, no intrinsic value • V : voucher that provides proof of the following: (i) exist a tamperproof one-to-one link between c. A and σA , and (ii) Charlie can compute σA using c. A if needed.

RELATED WORK ¢ four types of optimistic fair-exchange protocols (categorized by fairness primitive creation) • (i) protocols using verifiable escrows • Pro: can apply to almost any signature scheme • Con: computation and communication overhead • (ii) protocols using verifiable encryptions • Pro: efficiency(less computation and communication overhead) • Con: vulnerable to security flaw (based on ad hoc techniques) • (iii) protocols using convertible undeniable signatures • con: also utilizes zero-knowledge proofs in the exchange protocol • Con: needs a different verification algorithm compare to standard signature • (iv) protocols using one-time tokens • Pro: no zero-knowledge proofs in the exchange protocol • Con: not a truly optimistic protocol, TTP has to be involved intermittently to replenish the exhausted one-time tokens.

TECHNICAL BACKGROUND Multisignatures(1/2) ¢ multisignature scheme l ¢ Multiple-signers signature has little or no difference in size with an individual signature multisignatures are compatible with the underlying (single-signer) signature scheme. most convertible undeniable signatures not l algorithm is identical between multisignature verifying and underlying signature scheme verifying l

TECHNICAL BACKGROUND Multisignatures (2/2) ¢ a typical multisignature scheme l l l l l n (>=2) signers, 1 verifier ski : partial private key of signer i σi : partial signature created by partial private key ski pki : partial public key corresponding to ski sk : joint private key, sk = sk 1 +…+ skn σ : multisignature combined form the σi , and will send to the verifier pk : joint public key corresponding to sk verifier will verifies σ using pk If correctly, it is infeasible to create a multisignature using only a proper subset of {sk 1 , …, skn}

TECHNICAL BACKGROUND Our Multisignature Paradigm ¢ EXCHANGE ¢ a modified version of the typical multisignature model primary signer is the “owner” of the multisignature primary signer(Alice) ¢ sk 1( σ1(Alice’s commitment) 4. End by Bob ), with corresponding pk 1 • or initiates the dispute resolution protocol l sk 2 ( σ2 ) (no pk 2) l σ(Alice’s signature) : σ1 + ¢ 2 DISPUTE RESOLUTION σ 1. Initiate by Bob Cosigner(Charlie-TTP) ¢ ¢ 1. 2. Alice --- σ1, V --> Bob Alice <--- σB ----- Bob • Or Bob stop the protocol 3. Alice ---- σ ----> Bob • Or Alice stop the protocol l l ¢ • If σ is invalid(4) or Bob do not receive(3) 1. Bob --- σ1, V, σB --> Charlie sk 2( σ2 ) Verifier(Bob) l σB • Charlie compute σ 1. Bob <---- σ ---- Charlie 2. Alice <---- σB ---- Charlie

TECHNICAL BACKGROUND The RSA Signature Scheme ¢ RSA Scheme • p, q : big primes ; N = p * q • e : public key • random integer e, 1<e<ψ(N), such that gcd(e, ψ(N))=1 • ψ(N) : Euler totient function. number of integers in the interval [1, N] that are relatively prime to N • ψ(N) = (p-1)*(q-1) when p, q are primes • d : private key • unique integer d, 1<d<ψ(N), such that ed = 1(mod ψ(N) ¢ signature generation on message M l σ = H(M)dmod N • H: {0, 1}* ZN : public hash function • ZN : signature space , the set of integers modulo N • {0, 1}* denotes a binary string of arbitrary finite length ¢ Signature validation l σemod. N = H(M)

TECHNICAL BACKGROUND ¢ ¢ Our RSA-Based Multisignature Scheme(1/4) Boyd’scheme splits d multiplicatively l d = d 1 d 2(mod ψ(N) ) l H(M)d = H(M) d 1 d 2(mod N) We split d additively l p, q : safe primes • p = 2 p’+1, q = 2 q’+1, p’, q’ are all primes l l ZN* : multiplicative group of integers modulo N QN : the set of quadratic residues modulo N • signing space • QN = {a | a ZN* , there exists an x ZN* with x 2=a(mod. N)} • QN is a cyclic subgroup of ZN* , QN ZN* • |QN| = | ZN*| / 4 = p’q’ = λ

TECHNICAL BACKGROUND Our RSA-Based Multisignature Scheme(2/4) l H(M)d = H(M) d 1 * H (M) d 2(mod N) • H: {0, 1}* QN : public hash function l partial public key e 1 • d 1 e 1 = (mod λ) ¢ Lemma : l l l Let N = pq, where p = 2 p’ + 1, q = 2 q’ + 1, and p, q, p’, q’ are all prime numbers. Assume p < q. Then, 1. The order of elements in ZN* is one of the integers in the set { 1, 2, p’, q’, 2 p’, 2 q’, p’q’, 2 p’q’} 2. Given an element a ZN* {-1, 1} such that ord(a) < p’q’, then either gcd(a-1, N) or gcd(a+1, N) is a prime factor of N

TECHNICAL BACKGROUND Our RSA-Based Multisignature Scheme(3/4) ¢ characteristic of the elements of QN l For all b QN, b≠+-1, if gcd(b+1, N) and gcd(b-1, N) are not prime factors of N, then ord(b) = p’q’ keys satisfy the • If b QN , then ord(b) is one of {a, p’, q’, p’q’} • By Lagrange's Theorem and |QN| = p’q’ ¢ KEY GENERATION • p, q : safe primes ; N = p * q • e : joint public key following relations : ed = 1(mod λ) e 1 d 1 = 1(mod λ) d 1 + d 2 = d (mod λ) • random integer e, 1<e< λ, such that gcd(e, λ)=1 • d : joint private key • unique integer d, 1<d< λ, such that ed = 1(mod λ) • e 1, d 1: e 1 d 1 = 1(mod λ), similar to above • d 2 : cosigner’s partial private key, d 2 = d – d 1 (mod λ)

TECHNICAL BACKGROUND Our RSA-Based Multisignature Scheme(4/4) ¢ SIGNATURE GENERATION l l l σi = H(M)d i mod N, i =1, 2 H(M)d = σ1 * σ2 = H(M) d 1+d 2(mod N) Signature validation • σ1 e 1 mod N = H(M) • σ e mod N = H(M) ¢ splitting d multiplicatively(Boyd’scheme) in the protocol is insecure l l l (e * d 2 – e 1) is a mulyiple of λ cosigner can factor N efficiently using Koblitz's probabilistic algorithm by λ compute d 1 via the extended Euclidean algorithm

TECHNICAL BACKGROUND THE FAIREXCHANGE PROTOCOL(1/3) ¢ Players • Alice(primary signer, customer) • Charlie(cosigner, TTP) • Bob(verifier, merchant) ¢ REGISTRATION l Alice prove to Charlie • e 1 d 1 = 1(mod λ) • e(d 1 +d 2)= 1(mod λ) • without revealing d 1 and λ (Charlie knows the rest of the keys) l Charlie sends VC to Alice • VC : voucher created by Charlie signing on e 1 • VC assures the following: (i) verification of e 1 to Alice, and (ii) verification of the keys’ algebraic relations • and, as a result, Charlie can generate a multisignature from the corresponding partial signature

TECHNICAL BACKGROUND THE FAIREXCHANGE PROTOCOL (2/3) ¢ EXCHANGE 1. 2. Alice ---CCA , σ1, Vc --> Bob Alice <--- Eγ(μ) ----- Bob • 3. Alice ---- σ ----> Bob • 4. l l l Or Alice stop the protocol End by Bob • l Or Bob stop the protocol or initiates the dispute resolution protocol σ1 and Vc constitute the fairness primitive c. A and V CCA: certificate by Certificate Authority(CA) certifing e and N Eγ(μ): encrypted merchandise, constitute the σB σ as σA

TECHNICAL BACKGROUND THE FAIREXCHANGE PROTOCOL (3/3) ¢ DISPUTE RESOLUTION 1. Initiate by Bob • If σ is invalid(4) or Bob do not receive σ(3) • Bob --- σ1, Vc, Eγ(μ), CCA , M--> Charlie 2. Charlie compute σ • σ = σ1 * H(M)d 2 (mod N) • Bob <---- σ ------ Charlie • Alice <---- Eγ(μ) ---- Charlie

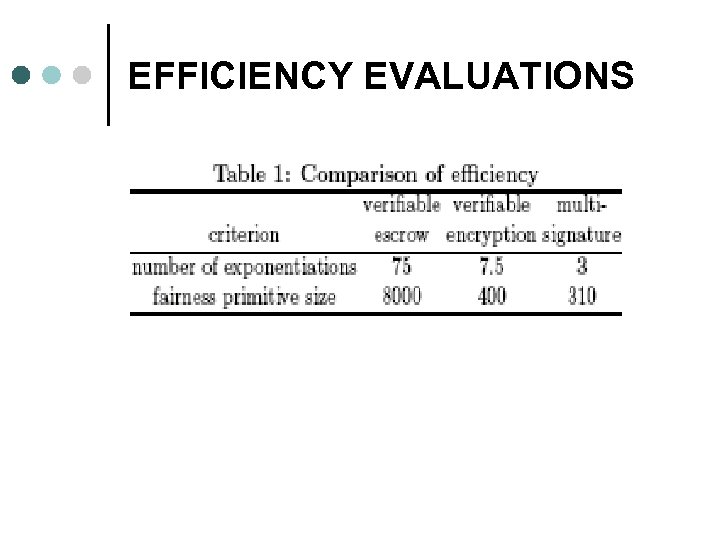
EFFICIENCY EVALUATIONS

CONCLUSIONS ¢ a novel multisignature paradigm • which is quite different from the conventional model • a novel method for constructing efficient optimistic fair-exchange protocols using RSA-based multisignatures. ¢ Advantages of Our approach l Efficient • No zero-knowledge proofs in the exchange protocol, only in the registration phase l Simple • uses multisignatures that are compatible with the underlying (single-signer) signature l Flexible • Can be applied to constructing fair-exchange protocols via multisignatures based on signature algorithms other than RSA • can be used with the protocol framework of Asokan et al