Constructing a Large Node Chow-Liu Tree Based on

Constructing a Large Node Chow-Liu Tree Based on Frequent Itemsets Kaizhu Huang, Irwin King, Michael R. Lyu Multimedia Information Processing Laboratory The Chinese University of Hong Kong Shatin, NT. Hong Kong {kzhuang, king, lyu}@cse. cuhk. edu. hk ICONIP 2002, November 19, 2002 Orchid Country Club, Singapore

Outline v. Background n n Probabilistic Classifiers Chow-Liu Tree v. Motivation v. Large Node Chow-Liu tree v. Experimental Results v. Conclusion

A Typical Classification Problem v. Given a set of symptoms, one wants to find out whether these symptoms give rise to a particular disease.

Background a constant for a given instance of A 1, A 2, …An v. Probabilistic Classifiers The classification function is defined as: The joint probability is not easily estimated from the dataset; thus the assumption about the distribution has to be made, dependence or independence relationship among variables. n

Background v. Chow-Liu Tree (CLT) n Assumption: a dependence tree exists among the variables, given the class variable C. A tree dependence structure

Background v. Chow-Liu Tree n Advantages l l n Class Variable Comparable with some of the state-of-the-art classifiers. The tree structure enables it a resistance to the over-fitting problem and a decomposition characteristic. Disadvantages l It cannot model non-tree dependence relationship among attributes or variables.

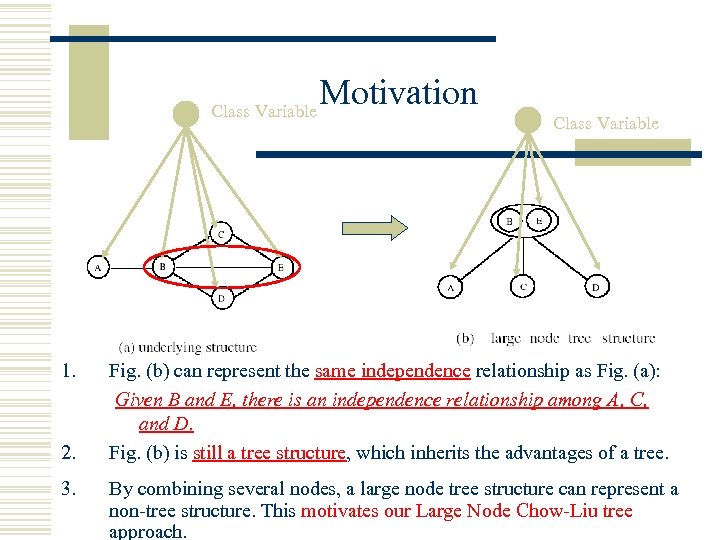
Class Variable 1. 2. 3. Motivation Class Variable Fig. (b) can represent the same independence relationship as Fig. (a): Given B and E, there is an independence relationship among A, C, and D. Fig. (b) is still a tree structure, which inherits the advantages of a tree. By combining several nodes, a large node tree structure can represent a non-tree structure. This motivates our Large Node Chow-Liu tree approach.

Overview of Large Node Chow-Liu Tree (LNCLT) Underlying structure Step 1: draft the Chow. Liu tree Step 2: draft the Chow. Liu tree The same independence relationship Step 1. Draft the Chow-Liu tree Draft the CL-tree of the dataset according to the CLT algorithm. Step 2. Refine the Chow-Liu tree based on some combination rules Refine the Chow-Liu tree into a large node Chow-Liu tree based on some combination rules

Combination Rules v Bounded cardinality The cardinality of each large node should not greater than a bound “k”. v Frequent Itemsets Each large node should be Frequent itemset. v Father-son or sibling relationship The nodes in a large node should be a father-son or sibling relationship.

Combination Rules (1) 1. Bounded Cardinality n n The cardinality of each large node ( the number of nodes in a large node) should not greater than a bound “k”. An example is that: if we set “k” as the number of the attributes or variables, the LNCLT will be a “one large node tree”, which will lose all the merits as a tree. “One node tree” will lose all the merits of the “tree”.

Combination Rules (2) v. Frequent Itemsets Food store example: In a food store, if you buy {bread}, it will be highly possible for you to buy {butter}. Thus {bread, butter} is called a frequent itemset. Frequent Itemset is the set of attributes that occur with each other frequently. Frequent Itemsets are possible “large nodes”, since the attributes in a Frequent Itemset act just like one “attribute”— they occur with each other frequently at the same time.

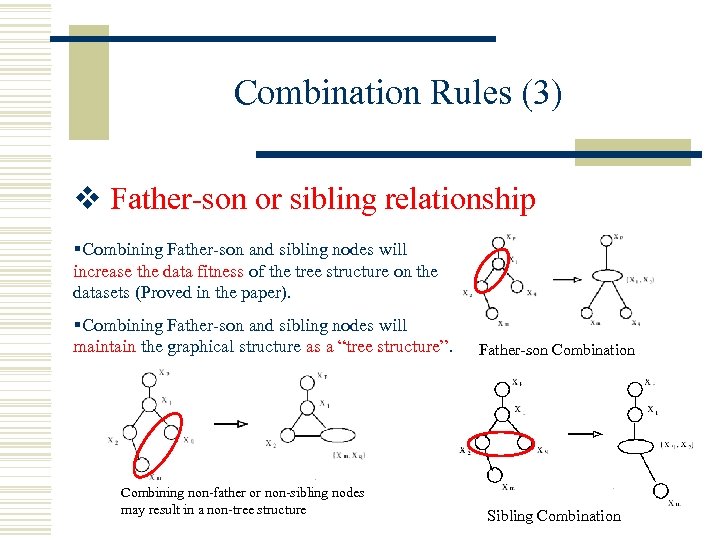
Combination Rules (3) v Father-son or sibling relationship §Combining Father-son and sibling nodes will increase the data fitness of the tree structure on the datasets (Proved in the paper). §Combining Father-son and sibling nodes will maintain the graphical structure as a “tree structure”. Combining non-father or non-sibling nodes may result in a non-tree structure Father-son Combination Sibling Combination

Constructing Large Node Chow-Liu Tree 1. Generate the frequent itemsets Call Apriori[AS 94] to generate the frequent itemsets, which have the size less than k. Record all the frequent itemsets together with their frequnecy into list L. 2. Draft the Chow-Liu tree Draft the CL-tree of the dataset according to the CLT algorithm. 3. Combine nodes based on Combining rules Iteratively combine the frequent itemset with maximum frequency, which satisfy the combination conditions: father-son or sibling relationship until L is NULL.

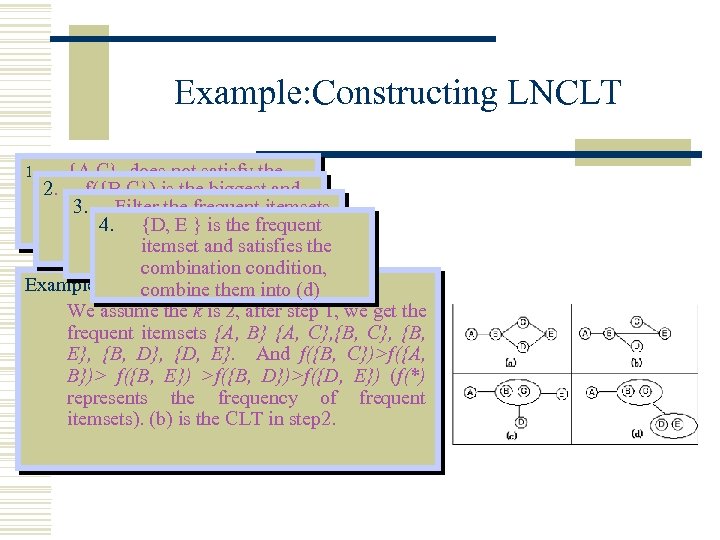
Example: Constructing LNCLT 1. {A, C} does not satisfy the 2. combination condition, filter f({B, C}) is the biggest and 3. . Filter the frequent satisfies out {A, C} combination itemsets 4. which combine them with {D, E } coverage condition, haveis the frequent into{B, C} , the {D, E} is left. (c)itemset and satisfies the combination condition, Example: combine them into (d) We assume the k is 2, after step 1, we get the frequent itemsets {A, B} {A, C}, {B, E}, {B, D}, {D, E}. And f({B, C})>f({A, B})> f({B, E}) >f({B, D})>f({D, E}) (f(*) represents the frequency of frequent itemsets). (b) is the CLT in step 2.

Experimental Setup v. Dataset: MNIST-handwritten digit (28*28 gray-level bitmap) database training dataset size: 60000 testing dataset size: 10000 v Experimental Environments n n Platform: win 2000 Developing tool: Visual C++ 6. 0

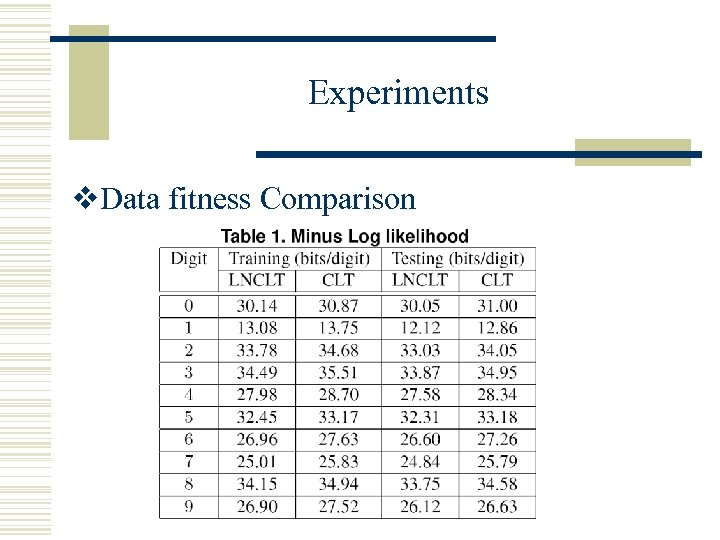
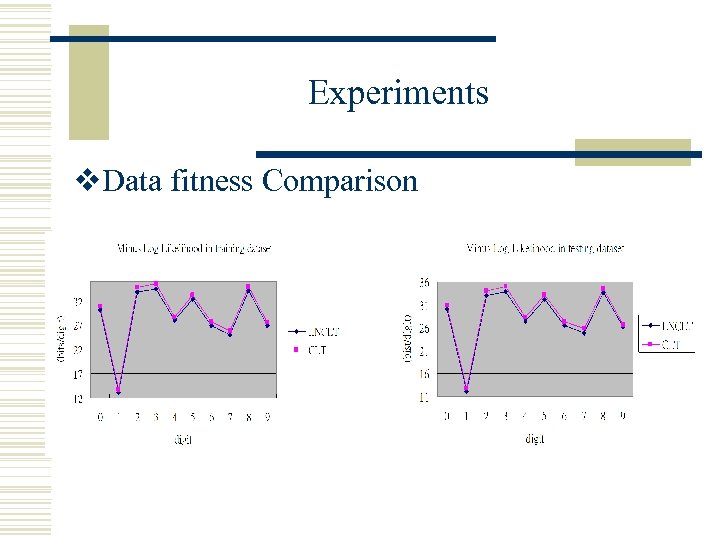
Experiments v. Data fitness Comparison

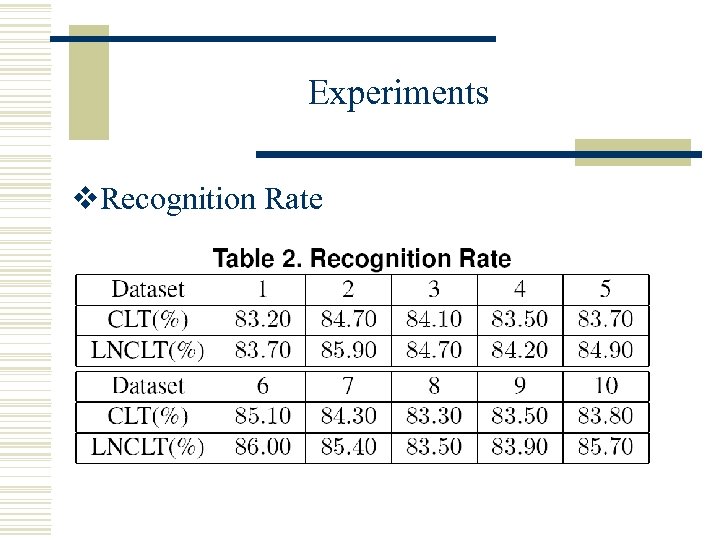
Experiments v. Recognition Rate

Future Work v. Evaluate our algorithm extensively in other benchmark datasets. v. Examine other combining rules.

Conclusion v A novel Large Node Chow-Liu tree is constructed based on Frequent Itemsets. v LNCLT can partially overcome the disadvantages of CLT, i. e. , inability to represent non-tree structures. v We demonstrate that our LNCLT model has a better data fitness and a better prediction accuracy theoretically and experimentally.

Main References w w w [AS 1994] R. Agrawal, R. Srikant, 1994, “Fast algorithms for mining association rules”, Proc. VLDB-94 1994. [Chow, Liu 1968] Chow, C. K. and Liu, C. N. (1968). Approximating discrete probability distributions with dependence trees. IEEE Trans. on Information Theory, 14, (pp 462 -467) [Friedman 1997] Friedman, N. , Geiger, D. and Goldszmidt, M. (1997). Bayesian Network Classifiers. Machine Learning, 29, (pp. 131 -161). [Cheng 1997] Cheng, J. Bell, D. A. Liu, W. 1997, Learning Belief Networks from Data: An Information Theory Based Approach. In Proceedings of ACM CIKM’ 97 [Cheng 2001] Cheng, J. and Greiner, R. 2001, Learning Bayesian Belief Network Classifiers: Algorithms and System, E. Stroulia and S. Matwin(Eds. ): AI 2001, LNAI 2056, (pp. 141 -151), w Learning Bayesian Belief Network Classifiers: Algorithms and System, E. Stroulia and S. Matwin(Eds. ): AI 2001, LNAI 2056, (pp. 141 -151).

Q&A Thanks.