Constraint Satisfaction Problems ECE 457 Applied Artificial Intelligence

Constraint Satisfaction Problems ECE 457 Applied Artificial Intelligence Spring 2007 Lecture #4

Outline n n Defining constraint satisfaction problems (CSP) CSP search algorithms n Russell & Norvig, chapter 5 ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 2

States n What do we know about states? n n n A state might be a goal (goal test) A state has a value (cost or payoff) An agent moves from state to state using actions The state space can be discreet or continuous Ties in with the problem definition n Initial state, goal test, set of actions and their costs defined in problem ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 3

Definitions n A constraint-satisfaction problem has n A set of variables n n Each variable has a domain of values n n Xi Di = {di 1, di 2, …, din} A set of constraints on the values each variable can take n n V = {X 1, X 2, …, Xn} C = {C 1, C 2, …, Cm} A state is a set of assignment of values n S 1 = {X 1 = d 12, X 4 = d 45} ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 4

Definitions n Consistent (legal) state n n Complete state n n Does not violate any constraints All variables have a value Goal state n n Consistent and complete Might not exist n Proof of inconsistency ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 5

Example: 8 -queen n Variables: 64 squares n n Values: Queen or no queen n n Xi, j D = {queen, empty} States: All board configurations n n V = {X 1, 1, X 1, 2, …, X 64, 64} 1. 8 x 1014 complete states Constraints: Attacks n n {Xi, j = queen Xi, j+n = empty, Xi, j = queen Xi+n, j+n = empty} 92 complete and consistent states ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 6

Example: 8 -queen ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 7

Example: The Einstein Puzzle n There are 5 houses in 5 different colours. In each house lives a person with a different nationality. These 5 owners drink a certain beverage, smoke a certain brand of cigar and keep a certain pet. No owners have the same pet, smoke the same brand of cigar or drink the same drink. Who keeps the fish? n n n n The The The The English lives in a red house. Swede keeps dogs as pets. Dane drinks tea. green house is on the left of the white house. green house owner drinks coffee. person who smokes Pall Mall rears birds. owner of the yellow house smokes Dunhill. man living in the house right in the centre drinks milk. Norwegian lives in the first house. man who smokes Blend lives next to the one who keeps cats. man who keeps horses lives next to the man who smokes Dunhill. owner who smokes Blue Master drinks beer. German smokes Prince. Norwegian lives next to the blue house. man who smokes Blend has a neighbour who drinks water. ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 8

Example: The Einstein Puzzle 1 n 3 4 5 25 variables n n 2 V = {N 1, …, N 5, C 1, …, C 5, D 1, …, D 5, S 1, …, S 5, P 1, …, P 5} Domains n n n Ni {English, Swede, Dane, Norwegian, German} Ci {green, yellow, blue, red, white} Di {tea, coffee, milk, beer, water} Si {Pall Mall, Dunhill, Blend, Blue Master, Prince} Pi {dog, cat, horse, fish, birds} ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 9

Example: The Einstein Puzzle n The Norwegian lives in the first house. n n The English lives in a red house. n n N 1 = Norwegian (Ni = English) (Ci = Red) The green house is on the left of the white house. n n n (Ci = green) (Ci+1 = white) (C 5 ≠ green) (C 1 ≠ white) ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 10

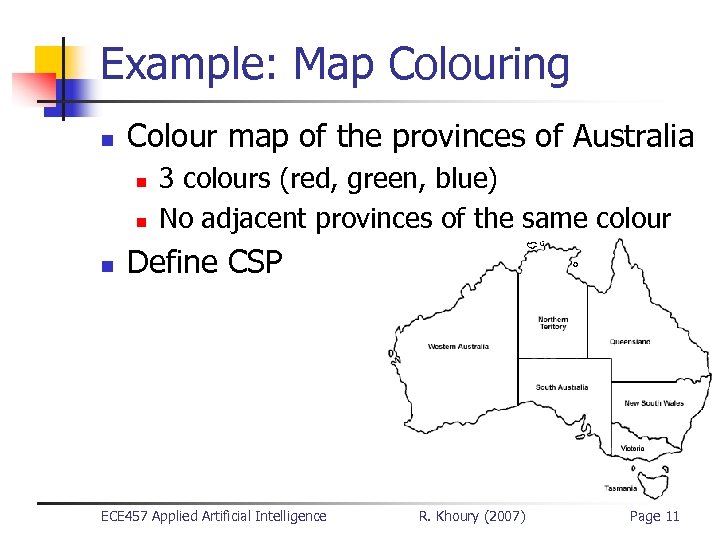
Example: Map Colouring n Colour map of the provinces of Australia n n n 3 colours (red, green, blue) No adjacent provinces of the same colour Define CSP ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 11

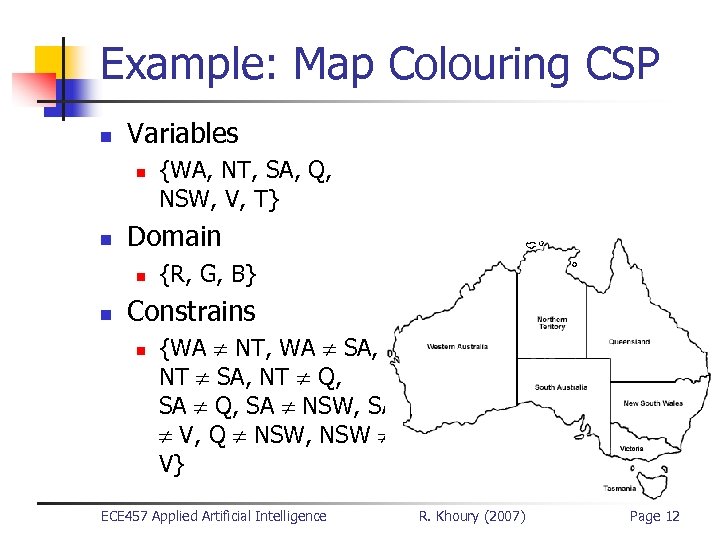
Example: Map Colouring CSP n Variables n n Domain n n {WA, NT, SA, Q, NSW, V, T} {R, G, B} Constrains n {WA NT, WA SA, NT Q, SA NSW, SA V, Q NSW, NSW V} ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 12

Solving CSP n Iterative improvement methods n n Start with random complete state, improve until consistent Tree searching n Start with empty state, make consistent variable assignments until complete ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 13

Iterative Improvement n Algorithm: n n Start with random complete state While not consistent n n n Not complete n n n Pick a variable (randomly or with a heuristic) Change its assignment to minimize number of violated constraints Might not search all state space Might not find a solution even if one exists We won’t do that in this course ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 14

Tree Search n Formulate CSP as tree n n n Root node: no variables are assigned a value Action: assign a value if it does not violate any constraints Solution node at depth n for n-variable problem ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 15

Backtracking Search n n Start with empty state While not complete n n Pick a variable (randomly or with heuristic) If it has a value that does not violate any constraints n n Assign that value Else n n Go back to previous variable Assign it another value ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 16

Backtracking Search n Depth-first search algorithm n n Algorithm complete n n n Goes down one variable at a time In a dead end, back up to last variable whose value can be changed without violating any constraints, and change it If you backed up to the root and tried all values, then there are no solutions Will find a solution if one exists Will expand the entire (finite) search space if necessary Depth-limited search with limit = n ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 17

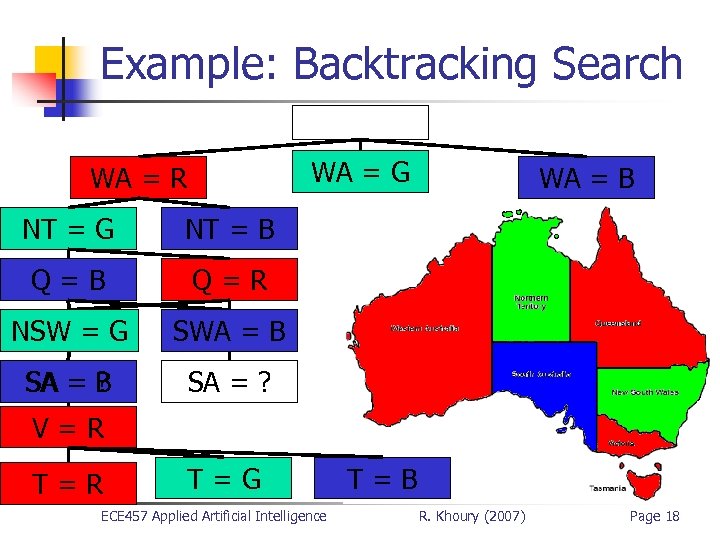
Example: Backtracking Search WA = G WA = R NT = G NT = B Q=R NSW = G NSW = B SWA R SA = B ? WA = B SA = ? V=R T=G ECE 457 Applied Artificial Intelligence T=B R. Khoury (2007) Page 18

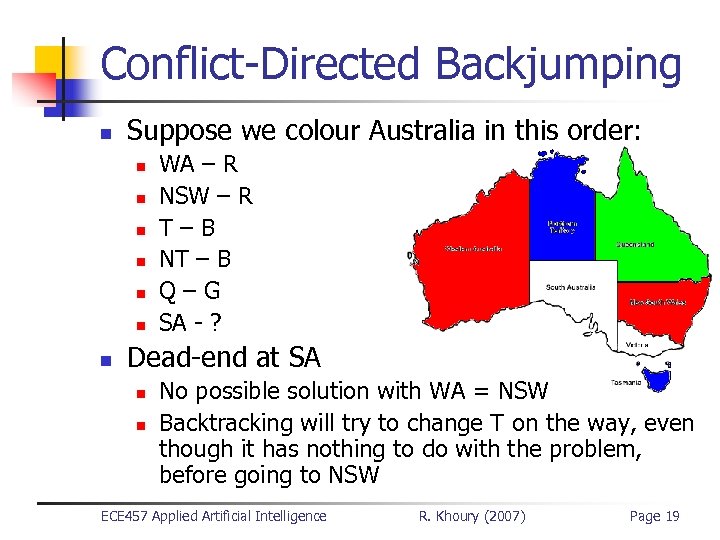
Conflict-Directed Backjumping n Suppose we colour Australia in this order: n n n n WA – R NSW – R T–B NT – B Q–G SA - ? Dead-end at SA n n No possible solution with WA = NSW Backtracking will try to change T on the way, even though it has nothing to do with the problem, before going to NSW ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 19

Conflict-Directed Backjumping n Backtracking goes back one level in the search tree at a time n n n Chronological backtrack Not rational in cases where the previous step is not involved to the conflict Conflict-directed backjumping (CBJ) n n n Should go back to a variable involved in the conflict Skip several levels if needed to get there Non-chronological backtrack ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 20

Conflict-Directed Backjumping n Maintain a conflict set for each variable n List of previously-assigned variables that are related by constraints conf(WA) = {} conf(NSW) = {} conf(T) = {} conf(NT) = {WA} conf(Q) = {NSW, NT} conf(SA) = {WA, NSW, NT, Q} n When we hit a dead-end, backjump to the deepest variable in the conflict set ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 21

Conflict-Directed Backjumping n Learn from the conflict by updating the conflict set of the variable we jumped to n n n Conflict at Xj, backjump to Xi conf(Xi)={X 1, X 2, X 3} conf(Xj)={X 3, X 4, X 5, Xi} conf(Xi) = conf(Xi) conf(Xj) – {Xi} conf(Xi) = {X 1, X 2, X 3, X 4, X 5} Xi absorbed the conflict set of Xj ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 22

Conflict-Directed Backjumping conf(WA) = {} conf(NSW) = {} conf(T) = {} conf(NT) = {WA} conf(Q) = {NSW, NT} conf(SA) = {WA, NSW, NT, Q} n SA backjump to Q n n n Q backjump to NT n n conf(Q) = {WA, NSW, NT} Meaning: “There is no consistent solution from Q onwards, given the preceding assignments of WA, NSW and NT together” conf(NT) = {WA, NSW} NT backjump over T to NSW n conf(NSW) = {WA} ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 23

Heuristics n Backtracking and CDJ searches are variations of depth-limited search n n n Uninformed search technique Can we make it an informed search? Add some heuristics n n n Which variable to assign next? In which order should the values be tried? How to detect dead-ends early? ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 24

Variable & Value Heuristics n Most constrained variable n n n Most constraining variable n n Choose the variable with the fewest legal values remaining in its domain aka Minimum remaining values Choose the variable that’s part of the most constraints Useful to pick first variable to assign aka Degree heuristic Least constraining variable n n Pick the variable that’s part of the fewest constrains Keeps maximum flexibility for future assignments ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 25

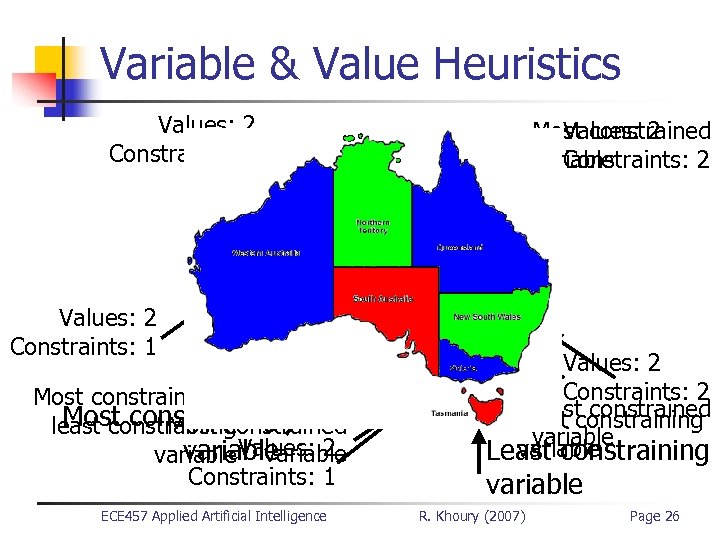
Variable & Value Heuristics Values: 2 Constraints: 2 Values: 2 Constraints: 1 Most constrained & Most constraining Most constrained least constraining variable Values: 2 Constraints: 1 ECE 457 Applied Artificial Intelligence Most constrained Values: 2 variable Constraints: 2 Values: 2 Constraints: 2 Most constrained Most constraining variable Least constraining variable R. Khoury (2007) Page 26

Forward Checking n n How to detect dead-ends early? Keep track of the domain of unassigned variables n n n Use constraints to prune domain of unassigned variables Backtrack when a variable has an empty domain Do not waste time exploring further ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 27

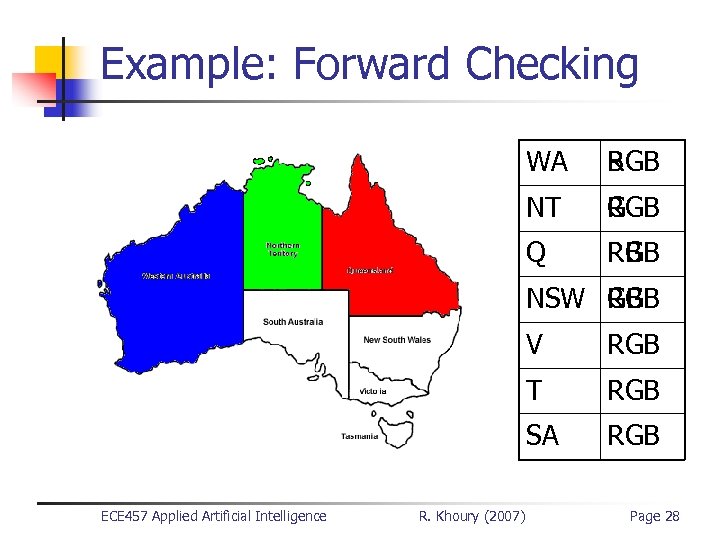
Example: Forward Checking WA B RGB NT G RG RGB Q R RB RGB NSW RGB GB V T R. Khoury (2007) RGB SA ECE 457 Applied Artificial Intelligence RGB R RG RGB Page 28

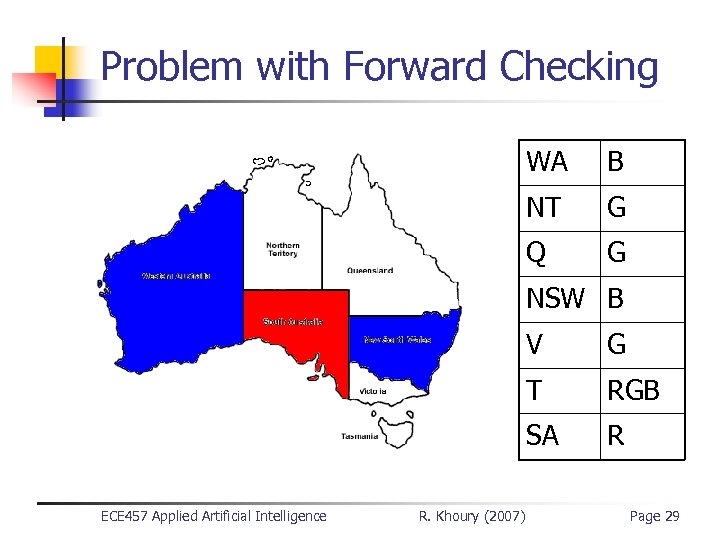
Problem with Forward Checking WA B NT G Q G NSW B V T R. Khoury (2007) RGB SA ECE 457 Applied Artificial Intelligence G R Page 29

Constraint Propagation n n Propagate the consequences of a variable’s constraints onto other variables Represent CSP as NT constraint graph WA n n n Nodes are variables Arcs are constraints Q NSW SA Check for consistency V T ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 30

Checking for Consistency n Node consistency n n n Arc consistency n n n Unary constraint (e. g. NT G) A node is consistent if and only if all values in its domain satisfy all unary constraints Binary constraint (e. g. NT Q) An arc Xi Xj or (Xi, Xj) is consistent if and only if, for each value a in the domain of Xi, there is a value b in the domain of Xj that is permitted by the binary constraints between Xi and Xj. Path consistency n Can be reduced to arc consistency ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 31

Checking for Consistency n Node consistency n n Simply scan domain of values of each variable and remove those that are not valid Arc consistency n Examine edges and delete values from domains to make arcs consistent ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 32

Checking for Consistency n Remove inconsistent values from a variable’s domain n Backtrack if empty domain Maintaining node and arc consistency reduces the size of the tree More computationally expensive than Forward Checking, but worth it ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 33

AC-3 Algorithm n n Keep queue of arcs (Xi, Xj) to be checked for consistency If checking an arc removes a value from the domain of Xi, then all arcs (Xk, Xi) are reinserted in the queue ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 34

AC-3 Algorithm n n Add all arcs to queue While queue not empty n n Get next arc from queue For each value di of Xi n If there is no consistent value dj in Xj n n Delete di If a value di was deleted n For each neighbour Xk of Xi n Add arc (Xk, Xi) to queue ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 35

AC-3 Algorithm n Advantages n n n Prunes tree, reduces amount of searching For n-node CSP that’s n-consistent, solution is guaranteed with no backtracking Disadvantage n Computationally expensive n If pruning takes longer than searching, it’s not worth it ECE 457 Applied Artificial Intelligence R. Khoury (2007) Page 36