256e21b5e51283a70b4d08f87db957ac.ppt
- Количество слайдов: 67

Constraint Satisfaction Problems & Constraint Programming Representing Knowledge with Constraints x 1 x 2 x 6 x 3 x 5 KNOWLEDGE REPRESENTATION & REASONING x 4 1

KR&R for Combinatorial Problems n Many, many practical applications g Resource allocation, scheduling, routing, frequency n Sports scheduling example assignment, timetabling, vehicle routing, etc. g In sports league scheduling we try to build the schedule of matches between teams (e. g. football teams). There are n Properties various constraints: g Computationally difficult · Each team must play each other exactly twice (once home and once away) g Technical and modeling expertise needed · g Experimental in nature No team can play more than two consecutive home or away matches g Important ($$$) in practice · The number of times that a team plays two consecutive n Many solution techniques home or away matches must be minimum · Teams that use the same stadium cannot play home games g (Mixed) integer programming at the same date g Specialized methods · Games between top teams must occur at certain dates (due g Local search/metaheuristics to TV coverage) g Constraint programming · Etc. KNOWLEDGE REPRESENTATION & REASONING 2

Quotations n “Constraint programming represents one of the closest approaches computer science has yet made to the Holy Grail of programming: the user states the problem, the computer solves it. ” Eugene C. Freuder, Constraints, April 1997 n “Were you to ask me which programming paradigm is likely to gain most in commercial significance over the next 5 years I’d have to pick Constraint Programming, even though it’s perhaps currently one of the least known and understood. ” Dick Pountain, BYTE, February 1995 KNOWLEDGE REPRESENTATION & REASONING 3
Constraint Programming n Constraint programming is the continuous dream of programming x 1 g State the constraints g The solver will find a solution n Knowledge representation with constraints is the preferred model in many domains g Scheduling Vehicle routing g Resource allocation g Temporal Reasoning g … g KNOWLEDGE REPRESENTATION & REASONING x 2 x 6 x 3 x 5 x 4 4

What is Constraint Programming? n Broad Answer: Programming where the use of constraints plays a central role g · alternative to logic programming, functional programming, object- oriented programming · there are constraint programming languages that support this n What is a constraint? g Let X 1, X 2, . . . , Xn be a finite sequence of variables, each associated with a domain, D 1, D 2, . . . , Dn. g A constraint on X 1, X 2, . . . , Xn is a relation D 1 × D 2 × · · · × Dn · can be defined explicitly/extensionally or implicitly/intentionally KNOWLEDGE REPRESENTATION & REASONING 5

What is Constraint Programming? n Narrow Answer: A more specific answer is obtained by programming with constraints in a particular manner. g Constraint programming involves solving a problem by: g · Modelling: Formulate the problem as a finite set of constraints (a Constraint Satisfaction Problem). · Solving: Solve the CSP, perhaps by using a constraint programming language · Mapping: Map the solution to the CSP to a solution to the original problem KNOWLEDGE REPRESENTATION & REASONING 6

What is a Constraint? n What is a constraint? g Let X 1, X 2, . . . , Xn be a finite sequence of variables, each associated with a domain, D 1, D 2, . . . , Dn. g A constraint on X 1, X 2, . . . , Xn is a relation D 1 × D 2 × · · · × Dn · can be defined explicitly/extensionally or implicitly/intentionally There are constraints everywhere! explicit (0, 1, 0) (1, 0, 0) (1, 1, 1) implicit x+y>z Ø Ø Ø KNOWLEDGE REPRESENTATION & REASONING Room Myrto is occupied from 12: 00 until 15: 00 Traffic in the web < 100 Gbytes/sec Salary < 15 k Euro Train 1 must leave 20 minutes before train 2 arrives Exams for 1 st semester must be at least 2 days apart 7
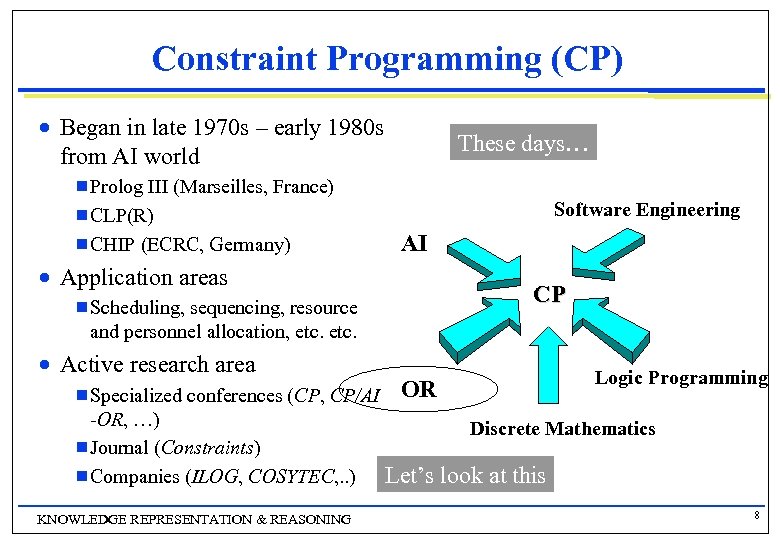
Constraint Programming (CP) n Began in late 1970 s – early 1980 s from AI world These days… g Prolog III (Marseilles, France) Software Engineering g CLP(R) g CHIP (ECRC, Germany) n AI Application areas CP g Scheduling, sequencing, resource and personnel allocation, etc. n Active research area g Specialized conferences (CP, CP/AI -OR, …) g Journal (Constraints) g Companies (ILOG, COSYTEC, . . ) KNOWLEDGE REPRESENTATION & REASONING Logic Programming OR Discrete Mathematics Let’s look at this 8

Constraint Programming n Two main contributions A new solving approach to combinatorial problems g · AI search methods and heuristics · Orthogonal and complementary to standard OR methods g A new language for representing combinatorial problems · Rich language for constraints · Much closer to the real problem than OR · Language for search procedures · Easily extensible KNOWLEDGE REPRESENTATION & REASONING 9
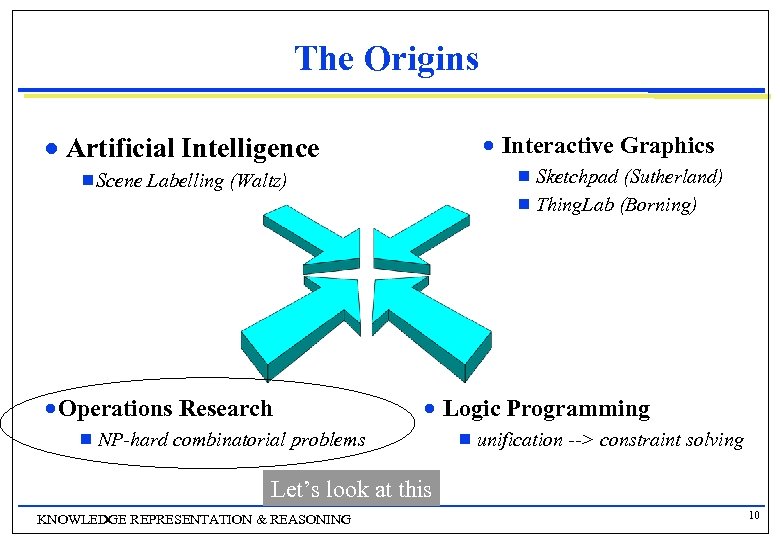
The Origins n Interactive Graphics Artificial Intelligence g Scene Sketchpad (Sutherland) g Thing. Lab (Borning) g Labelling (Waltz) Operations Research n g n Logic Programming n NP-hard combinatorial problems g unification --> constraint solving Let’s look at this KNOWLEDGE REPRESENTATION & REASONING 10

Integer Programming (IP) Consider the manufacture of television sets. A linear programming model might give a production plan of 205. 7 sets per week. n g No trouble stating that production should be 205 sets per week (or even ``roughly 200 sets per week''). Suppose we were buying warehouses to store finished goods. A model that suggests we buy 0. 7 warehouse at some location and 0. 6 somewhere else would be of little value. n g Warehouses come in integer quantities, and we would like our model to reflect that fact. This integrality restriction has far reaching effects. Modeling with integer variables has turned out to be useful far beyond restrictions to integral production quantities. With integer variables, one can model logical requirements, fixed costs, sequencing and scheduling requirements, and many other problem aspects. n KNOWLEDGE REPRESENTATION & REASONING 11

Integer Programming (IP) n The trouble with all this modeling power, however, is that problems with as few as 40 variables can be beyond the abilities of even the most sophisticated computers. Most real problems with more than 100 or so variables are not possible to solve unless they show specific exploitable structure. g Despite the possibility (or even likelihood) of enormous computing times, there are methods that can be applied to solving integer programs. g n An IP problem in which all variables are required to be integer is called a pure integer programming problem. g If some variables are restricted to be integer and some are not then the problem is a mixed integer programming problem (MIP). g The case where the integer variables are restricted to be 0 or 1 is called pure (mixed) 0 -1 programming problems or pure (mixed) binary integer programming problems. KNOWLEDGE REPRESENTATION & REASONING 12

Relationship to Linear Programming Given an integer program There is an associated linear program called the linear relaxation formed by dropping the integrality restrictions: Since (LR) is less constrained than (IP), the following are immediate: If (IP) is a minimization, the optimal objective value for (LR) is less than or equal to the optimal objective for (IP). n If (IP) is a maximization, the optimal objective value for (LR) is greater than or equal to that of (IP). n If (LR) is infeasible, then so is (IP). Solving (LR) does give some information: it gives a bound on the optimal value, and, if we are lucky, may give the optimal solution to IP. But for some problems it is very difficult to even get a feasible solution! feasible solution n KNOWLEDGE REPRESENTATION & REASONING 13
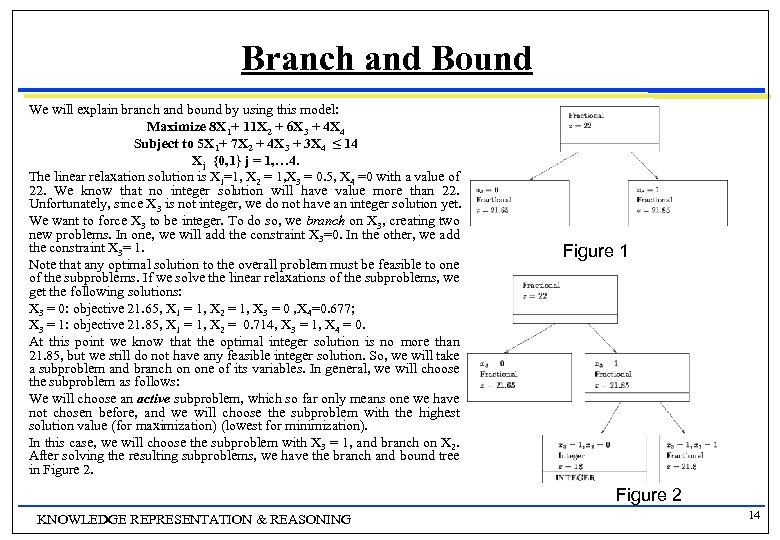
Branch and Bound We will explain branch and bound by using this model: Maximize 8 X 1+ 11 X 2 + 6 X 3 + 4 X 4 Subject to 5 X 1+ 7 X 2 + 4 X 3 + 3 X 4 ≤ 14 Xj {0, 1} j = 1, … 4. The linear relaxation solution is X 1=1, X 2 = 1, X 3 = 0. 5, X 4 =0 with a value of 22. We know that no integer solution will have value more than 22. Unfortunately, since X 3 is not integer, we do not have an integer solution yet. We want to force X 3 to be integer. To do so, we branch on X 3, creating two new problems. In one, we will add the constraint X 3=0. In the other, we add the constraint X 3= 1. Note that any optimal solution to the overall problem must be feasible to one of the subproblems. If we solve the linear relaxations of the subproblems, we get the following solutions: X 3 = 0: objective 21. 65, X 1 = 1, X 2 = 1, X 3 = 0 , X 4=0. 677; X 3 = 1: objective 21. 85, X 1 = 1, X 2 = 0. 714, X 3 = 1, X 4 = 0. At this point we know that the optimal integer solution is no more than 21. 85, but we still do not have any feasible integer solution. So, we will take a subproblem and branch on one of its variables. In general, we will choose the subproblem as follows: We will choose an active subproblem, which so far only means one we have not chosen before, and we will choose the subproblem with the highest solution value (for maximization) (lowest for minimization). In this case, we will choose the subproblem with X 3 = 1, and branch on X 2. After solving the resulting subproblems, we have the branch and bound tree in Figure 2. Figure 1 Figure 2 KNOWLEDGE REPRESENTATION & REASONING 14
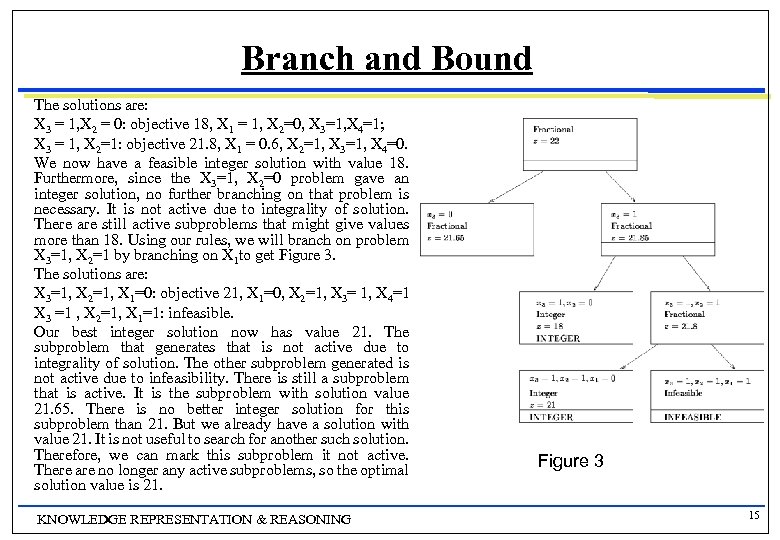
Branch and Bound The solutions are: X 3 = 1, X 2 = 0: objective 18, X 1 = 1, X 2=0, X 3=1, X 4=1; X 3 = 1, X 2=1: objective 21. 8, X 1 = 0. 6, X 2=1, X 3=1, X 4=0. We now have a feasible integer solution with value 18. Furthermore, since the X 3=1, X 2=0 problem gave an integer solution, no further branching on that problem is necessary. It is not active due to integrality of solution. There are still active subproblems that might give values more than 18. Using our rules, we will branch on problem X 3=1, X 2=1 by branching on X 1 to get Figure 3. The solutions are: X 3=1, X 2=1, X 1=0: objective 21, X 1=0, X 2=1, X 3= 1, X 4=1 X 3 =1 , X 2=1, X 1=1: infeasible. Our best integer solution now has value 21. The subproblem that generates that is not active due to integrality of solution. The other subproblem generated is not active due to infeasibility. There is still a subproblem that is active. It is the subproblem with solution value 21. 65. There is no better integer solution for this subproblem than 21. But we already have a solution with value 21. It is not useful to search for another such solution. Therefore, we can mark this subproblem it not active. There are no longer any active subproblems, so the optimal solution value is 21. KNOWLEDGE REPRESENTATION & REASONING Figure 3 15

Constraint Satisfaction Problems At the core of Constraint Programming KNOWLEDGE REPRESENTATION & REASONING 16

What is a Constraint Satisfaction Problem? n A constraint satisfaction problem (CSP) is defined by: g A set of variables X 1, …, Xn · Each variable Χi has a domain Di with its possible values g A set of constraints C 1, …, Cm · Each constraint involves a subset of the variables it specifies the allowed combinations of values for this subset 1 · A k-ary constraint C on a set of variables X 1, …, Xk is a subset of the Cartesian product D 1 x…x Dk {0, …, 5} · The set of variables in a constraint is called the constraint scope x n x 2 {0, …, 3} Binary and non-binary (or n-ary) constraint satisfaction problems KNOWLEDGE REPRESENTATION & REASONING 17

Constraint Satisfaction Problems n Solution of a CSP g Assignment of a value to each variable so that all constraints are satisfied n Goals: g Find one solution (feasibility problem) g Find all solutions g Find a solution that maximizes (or minimizes) some quantity · constraint optimization problem g Find an approximate “solution” All these tasks are NP-hard! (except perhaps one of them) KNOWLEDGE REPRESENTATION & REASONING 18
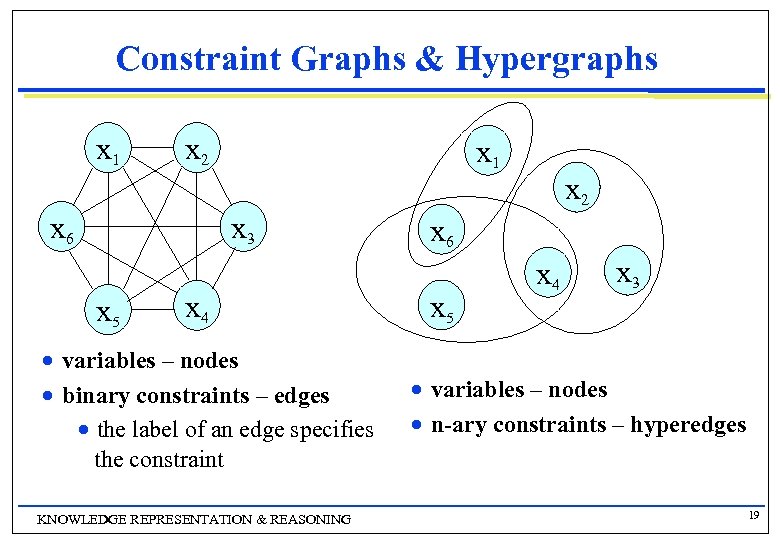
Constraint Graphs & Hypergraphs x 1 x 2 x 6 x 3 x 5 n n x 1 x 6 x 5 x 4 variables – nodes binary constraints – edges n the label of an edge specifies the constraint KNOWLEDGE REPRESENTATION & REASONING x 2 n n x 4 x 3 variables – nodes n-ary constraints – hyperedges 19
Example – Map Coloring We want to color each area in the map with a different color n We have three colors red, green, blue n KNOWLEDGE REPRESENTATION & REASONING 20

Example – Map Coloring Formal Definition: n Variables n g WA, NT, SA, Q, NSW, V, T n Domains (the same for all variables) g {red, green, blue} n Constraints g C(WA, NT) = {(red, green), (red, blue), (green, red), (green, blue), (blue, red), (blue, green)} g C(WA, SA) = … KNOWLEDGE REPRESENTATION & REASONING 21
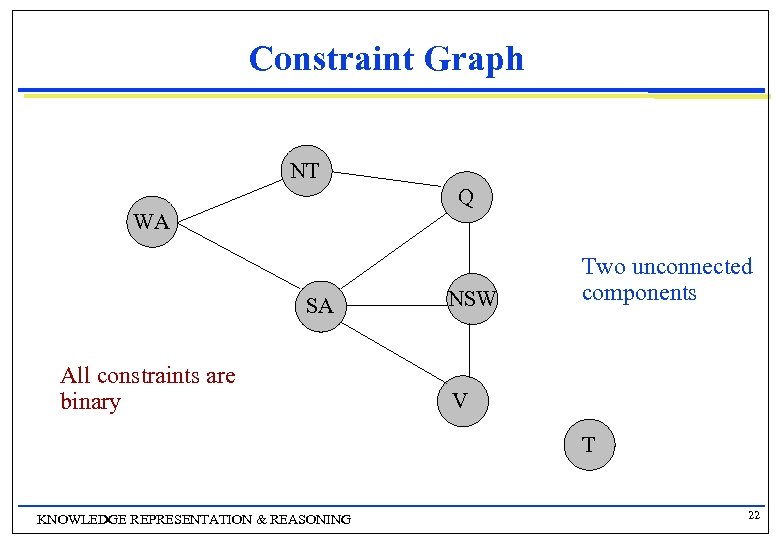
Constraint Graph NT Q WA SA All constraints are binary NSW Two unconnected components V T KNOWLEDGE REPRESENTATION & REASONING 22
Example – 8 Queens problem We want to place 8 queens on the chessboard so they can’t attack each other n KNOWLEDGE REPRESENTATION & REASONING 23

Example– 8 Queens problem n Formal Definition: n Variables g Each variable Xi (i=1, …, 8) represents the column where there is the i-th queen (i. e. the queen in the i-th row) n Domains g If the columns are represented by numbers from 1 to 8 then the domain of each variable Xi is Di = {1, 2, …, 8} KNOWLEDGE REPRESENTATION & REASONING 24

Παράδειγμα – 8 Queens problem n Constraints g There is a binary constraint C(Xi, Xj) for each pair of variables. These constraints can be defined as follows: g For all variables Xi and Xj , Xi Xj g For all variables Xi and Xj , if Xi = a and Xj = b then i – j a – b and i – j b – a KNOWLEDGE REPRESENTATION & REASONING 25
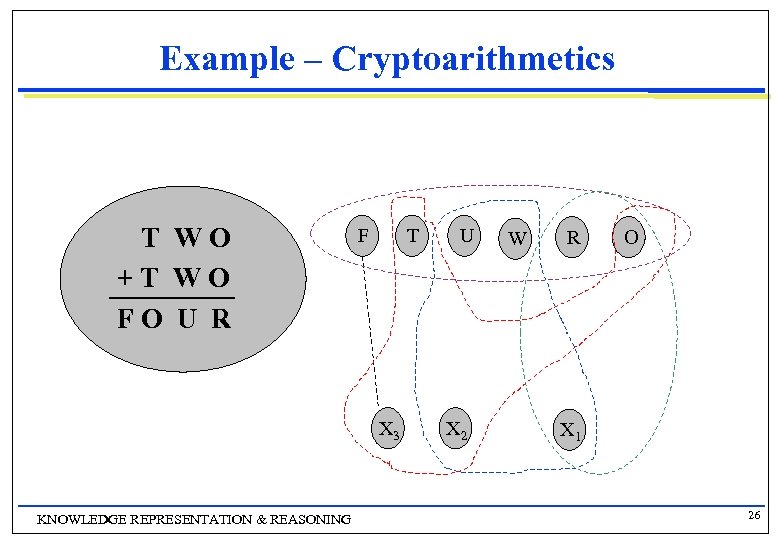
Example – Cryptoarithmetics T W O F T U W R O + T W O F O U R X 3 KNOWLEDGE REPRESENTATION & REASONING X 2 X 1 26

Example – Cryptoarithmetics Formal Definition: n Variables and Domains n g F, T, U, W, R, O {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} g X 1, X 2, X 3 {0, 1} n Constraints g alldifferent(F, T, U, W, R, O) T W O + T W O F O U R g O + O = R + 10 X 1 g X 1 + W = U + 10 X 2 + T = O + 10 X 3 g X 3 = F g KNOWLEDGE REPRESENTATION & REASONING 27
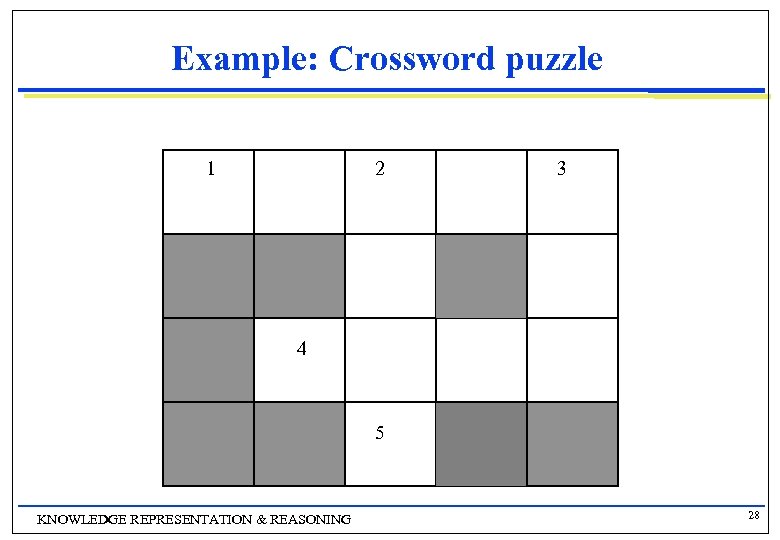
Example: Crossword puzzle 1 2 3 4 5 KNOWLEDGE REPRESENTATION & REASONING 28

Crossword puzzle as a CSP Variables and their domains n X 1 is 1 across g X 2 is 2 down g X 3 is 3 down g X 4 is 4 across g X 5 is 5 across g D 1 consists of all 5 -letter words in the dictionary D 2 consists of all 4 -letter words in the dictionary D 3 consists of all 3 -letter words in the dictionary D 4 consists of all 4 -letter words in the dictionary D 5 consists of all 2 -letter words in the dictionary Constraints (implicit/intensional) n C 12 is “the 3 rd letter of X 1 must equal the 1 st letter of X 2” g C 13 is “the 5 th letter of X 1 must equal the 1 st letter of X 3” g C 24 is … g C 25 is … g C 34 is. . . g KNOWLEDGE REPRESENTATION & REASONING 29
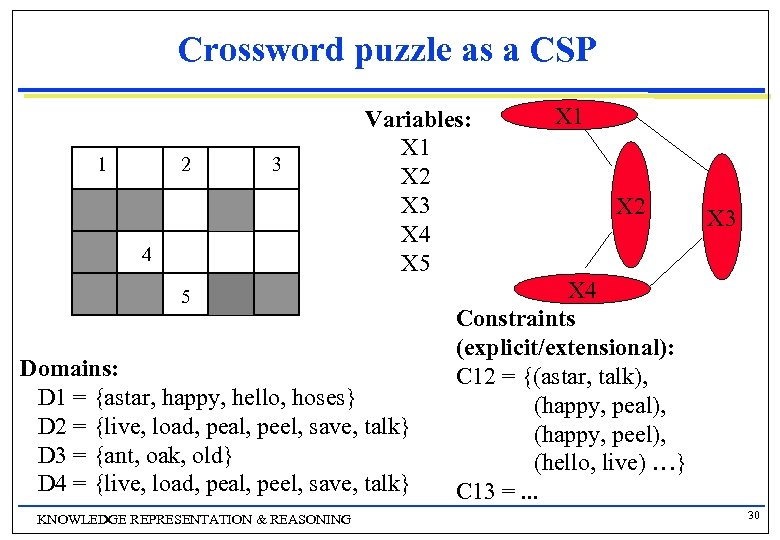
Crossword puzzle as a CSP 1 2 3 4 Variables: X 1 X 2 X 3 X 4 X 5 5 Domains: D 1 = {astar, happy, hello, hoses} D 2 = {live, load, peal, peel, save, talk} D 3 = {ant, oak, old} D 4 = {live, load, peal, peel, save, talk} KNOWLEDGE REPRESENTATION & REASONING X 1 X 2 X 3 X 4 Constraints (explicit/extensional): C 12 = {(astar, talk), (happy, peal), (happy, peel), (hello, live) …} C 13 =. . . 30

Real Constraint Satisfaction Problems n puzzles (not really practical applications, but they are fun) g N-queens, Zebra (five house puzzle), crossword puzzle, cryptoarithmetics (SEND+MORE=MONEY), mastermind n n n graph coloring analysis and synthesis of analog circuits option trading analysis cutting stock DNA sequencing crew scheduling chemical hypothetical reasoning warehouse location patient treatment scheduling airport counter allocation (Cathay Pacific Airways Ltd) crew rostering problem (Italian Railway Company) well activity scheduling (Saga Petroleum a. s. ) n KNOWLEDGE REPRESENTATION & REASONING 31

Early Commercial Applications (90 s) Lufthansa: Short-term staff planning. n Hongkong Container Harbor: Resource planning. n Renault: Short-term production planning. n Nokia: Software configuration for mobile phones. n Airbus: Cabin layout. n Siemens: Circuit verification. n Caisse d’epargne: Portfolio management. n KNOWLEDGE REPRESENTATION & REASONING 32

Applications in Research n Artificial Intelligence g Machine Vision g Natural Language Understanding g Temporal and Spatial Reasoning g Theorem Proving g Qualitative Reasoning § g Robotics § g Agents § g Planning KNOWLEDGE REPRESENTATION & REASONING § § Timetabling Scheduling Vehicle Routing Resource allocation Frequency Assignment 33

Applications in Research n Computer Science: g Program Analysis, Robotics, Agents n Molecular Biology, Biochemestry, Bioinformatics: g Protein Folding, Genomic Sequencing n Economics: g Scheduling, Stock Investment Planning n Linguistics: g Parsing n Medicine: g Decision Support n Physics: System Modeling KNOWLEDGE REPRESENTATION & REASONING 34

CSP Technology : Practical & Successful n Constraint satisfaction technology is one of the most successful examples of practical AI n There are many successful companies which build and trade CSP technology g ILOG g Cosytec g Parc Technologies g i 2 Technologies g IQ Software g … KNOWLEDGE REPRESENTATION & REASONING 35

CSP Technology : Practical & Successful! n n n n AKL n FSQP/CFSQP ALE n Goedel Amulet and Garnet n GNU-Prolog n ICE In. C++ library B-Prolog n IF/Prolog Bertrand n Brandeis Interval Arithmetic Constraint ILOG Numerica, ILOG Schedule, ILOG Solver n Interval Solver for Microsoft Excel Solver n JSolver n RISC-CLP(Real) CHIP n LIFE n SEL CIAL n MAC n ICStus CLAIRE n Newton n Screamer CLP n Nicolog n Star. FLIP++ CONFLEX' n Omega n Steeles constraint system' n Oz CPLEX n TOY n Pro. FIT n Toupie Cassowary n Prolog III, Prolog IV n Trilogy Contax n Pulsar n Unicalc Cooldraw, Deltablue, Skyblue, n QUAD-CLP(R) n cu-Prolog Thinglab. II n Quantum Leap n opbdp ECLi. PSe KNOWLEDGE REPRESENTATION & REASONING 36

A real CSP – Job-shop scheduling Examples of job shop scheduling problems include g factory scheduling problems, in which some operations have to be performed within one or several shifts g spacecraft mission scheduling problems, in which time windows are determined by astronomical events over which we have no control g patient treatment scheduling problems, in which a number of patients need to receive treatment that requires certain equipment within certain time windows, etc. n When solving a job shop CSP, the objective is to find as quickly as possible a feasible schedule, namely a schedule where each operation is performed within one of its legal time windows and no resource is oversubscribed. KNOWLEDGE REPRESENTATION & REASONING 37
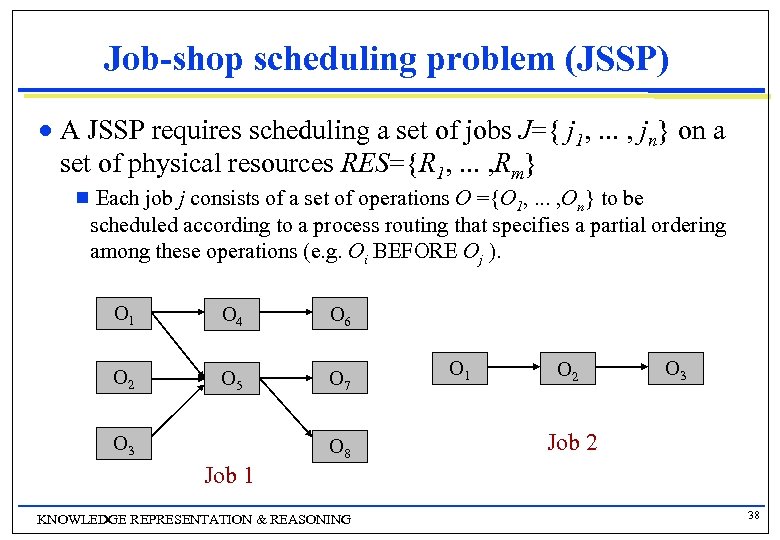
Job-shop scheduling problem (JSSP) n A JSSP requires scheduling a set of jobs J={ j 1, . . . , jn} on a set of physical resources RES={R 1, . . . , Rm} g Each job j consists of a set of operations O ={O 1, . . . , On} to be scheduled according to a process routing that specifies a partial ordering among these operations (e. g. Oi BEFORE Oj ). O 1 O 4 O 6 O 2 O 5 O 7 O 3 O 8 O 1 O 2 O 3 Job 2 Job 1 KNOWLEDGE REPRESENTATION & REASONING 38

Job-shop scheduling problem (JSSP) n n n Each job j has a release date rdj and a due date (or deadline) ddj between which all its operations have to be performed. Each operation Oi has a fixed duration dui and a start time sti whose value has to be selected. The domain of possible start times of each operation is initially constrained by the release and due dates of the job to which the operation belongs. g there can be additional unary constraints that further restrict the set of admissible start times of each operation, thereby defining one or several time windows within which an operation has to be carried out · e. g. a specific shift in factory scheduling n In order to be successfully executed, each operation Oi requires pi different resources (e. g. a machine) Rij (1 j pi ) KNOWLEDGE REPRESENTATION & REASONING 39

The JSSP as a CSP n Variables g A set of variables is associated with each operation, Oi, which consists of · the operation start time, sti · its resource requirements, Rij n Constraints g Precedence constraints defined by the process routings translate into linear inequalities of the type: sti +dui stj (i. e. Oi BEFORE Oj ) g Capacity constraints that restrict the use of each resource to only one operation at a time translate into disjunctive constraints of the form: ("p where Oi , Oj require Rp) sti +dui stj Ú stj +duj sti. These constraints simply express that, unless they use different resources, two operations Oi and Oj cannot overlap. KNOWLEDGE REPRESENTATION & REASONING 40
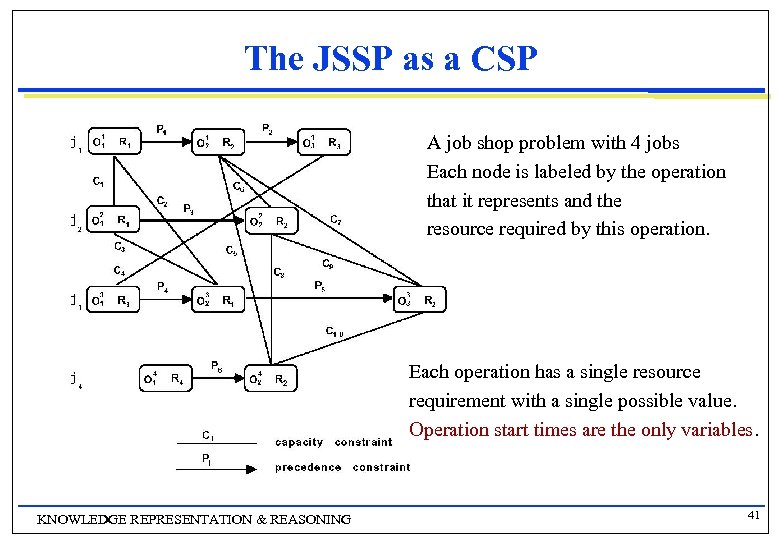
The JSSP as a CSP A job shop problem with 4 jobs Each node is labeled by the operation that it represents and the resource required by this operation. Each operation has a single resource requirement with a single possible value. Operation start times are the only variables. KNOWLEDGE REPRESENTATION & REASONING 41

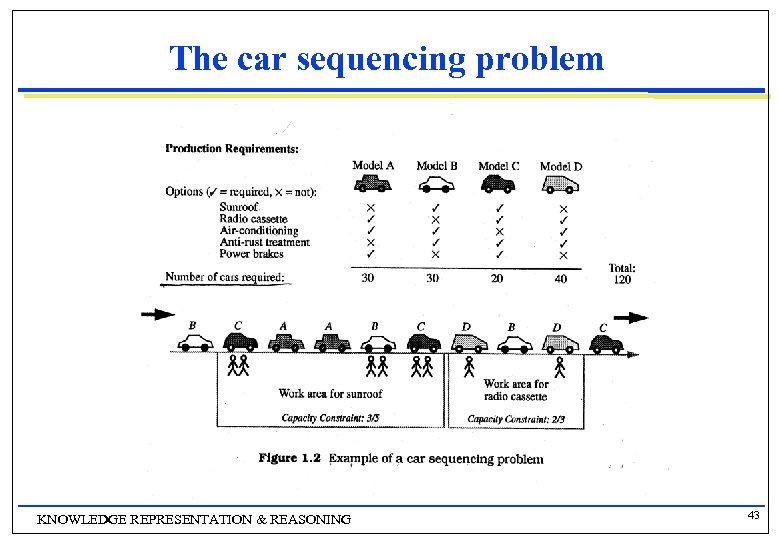
A real CSP – The car sequencing problem n n n In a car production scenario, cars are placed on conveyor belts which move through different work areas. A production line is normally required to produce cars of different models. The number of cars required for each model is called the production requirement. Each work area is constrained by its resource constraint or Capacity constraint. variable – one for every position in the conveyor belt (i. e. if there are n cars to be scheduled, the problem consists of n variables). domain - the set of car models, for example from model A to D. The task - to assign a value (a car model) to each variable (a position in the conveyor belt), satisfying both the production requirements and capacity constraints. KNOWLEDGE REPRESENTATION & REASONING 42
The car sequencing problem KNOWLEDGE REPRESENTATION & REASONING 43

Constraints and Databases n There are close links between CSPs and relational database theory Constraint terminology Database terminology CSP Variable Domain Constraint scope Constraint tuples Set of solutions KNOWLEDGE REPRESENTATION & REASONING Database Attribute domain Table schema Table instance Join of all tables 44

Constraints and Databases – Example n Consider the following CSP g A set of variables X = {x 0, …, x 9} g All variables have the domain D = {0, 1, 2} g There are constraints with the following scopes and allowed tuples: · c 1 = {x 0, x 1, x 3} – {(0, 0, 0), (0, 1, 0), (1, 0, 1), (1, 1, 1), (0, 1, 2)} · c 2 = {x 1, x 2, x 3} – {(0, 0, 0), (0, 0, 1), (1, 1, 0), (1, 0, 1), (0, 1, 2)} · c 3 = {x 1, x 4} – {(0, 0), (1, 1)} · c 4 = {x 3, x 6} – {(0, 0), (1, 1), (1, 0), (2, 0)} · c 5 = {x 4, x 5, x 6} – {(0, 0, 0), (0, 0, 1), (1, 1, 1), (1, 0, 2)} · c 6 = {x 4, x 7} – {(0, 1), (1, 0)} · c 7 = {x 5, x 8} – {(0, 1), (1, 0), (1, 1)} · c 8 = {x 6, x 9} – {(0, 0), (1, 1)} KNOWLEDGE REPRESENTATION & REASONING 45
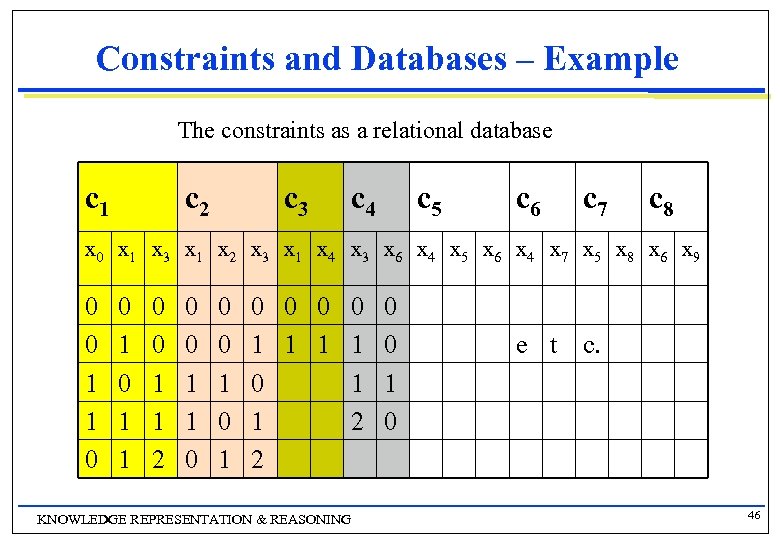
Constraints and Databases – Example The constraints as a relational database c 1 c 2 c 3 c 4 c 5 c 6 c 7 c 8 x 0 x 1 x 3 x 1 x 2 x 3 x 1 x 4 x 3 x 6 x 4 x 5 x 6 x 4 x 7 x 5 x 8 x 6 x 9 0 0 1 1 2 0 0 1 1 0 0 0 1 1 0 0 1 1 1 2 0 2 KNOWLEDGE REPRESENTATION & REASONING e t c. 46

Solving CSPs n Assuming we have expressed knowledge about a problem as a CSP g how can we reason with it? g how can we find a solution (if one exists)? g how can we find all solutions? g how can we infer new knowledge? Generate and test n Backtracking search algorithms n Approximation algorithms n Constraint propagation algorithms n KNOWLEDGE REPRESENTATION & REASONING 47

Solving CSPs n There are two general approaches to solving CSPs that are used in practice Systematic Search g · Explore systematically the space of all assignments · systematic = every valuation will be explored sometime · extends partial assignments g Local Search · explore the search space by small steps · start with an initial complete assignment · repairs complete assignments KNOWLEDGE REPRESENTATION & REASONING 48

First of all: Generate & Test Probably the most general problem solving method n Algorithm: n generate labelling test satisfaction Drawbacks: blind generator late discovery of inconsistencies KNOWLEDGE REPRESENTATION & REASONING Improvements: smart generator --> local search testing within generator --> backtracking 49

Generate and test: Crossword Puzzle n Try each possible combination until you find one that works: g astar – live – ant – live 1 2 3 g astar – live – ant – load g astar – live – ant – peal g… 4 5 Doesn’t check constraints until all variables have been instantiated n Very inefficient way to explore the space of possibilities (4*6*3*6 = 432 for this trivial problem, most inconsistent) n KNOWLEDGE REPRESENTATION & REASONING 50

Search Algorithms for CSPs A general search algorithm for CSPs n Initial State n g No value has been assigned to any variable n Actions g Assign a value from Di to an unassigned variable Xi n Goal Test g All variables have been assigned and all constraints are satisfied n The order in which the actions are executed does not matter g We can take advantage of this! KNOWLEDGE REPRESENTATION & REASONING 51

The Search Space of CSPs The search space is finite n The depth of the search tree is specified n g Equal to the number of variables n Solutions are always at the leaves of the search tree Leaves KNOWLEDGE REPRESENTATION & REASONING 52

Search Algorithms for CSPs n Which generic AI search algorithm looks suitable for CSPs? n Breadth-First Search ? g No! BFS will be inefficient because solutions are always at the leaves n Depth-First Search ? g Better than BFS. But it will frequently waste time searching while constraints are already violated n Hill Climbing ? g Minimize conflicts KNOWLEDGE REPRESENTATION & REASONING 53

Search Algorithms for CSPs n We will study variations of DFS especially for CSPs. g These algorithms are based on backtracking search Simple (or Chronological) Backtracking (BT) n Backjumping (BJ) n Forward Checking (FC) n FC with Conflict-based Backjumping (FC-CBJ) n Maintaining Arc Consistency (MAC) n Also two variations of hill climbing g Min-conflicts with Random Walk KNOWLEDGE REPRESENTATION & REASONING 54

Chronological Backtracking (ΒΤ) n n The basic idea in all systematic backtracking-based algorithms is to start with a partial solution (i. e. assignments of a subset of the variables) and continue assigning variables until we reach a complete solution BT follows this technique g Consider the variables in some order g Pick an unassigned variable and give it a provisional value such that it is consistent with all of the constraints g If no such assignment can be made, we’ve reached a dead end and need to backtrack to the previous variable and try its next value g Continue this process until a solution is found or we backtrack to the initial variable and have exhausted all possible valaues KNOWLEDGE REPRESENTATION & REASONING 55
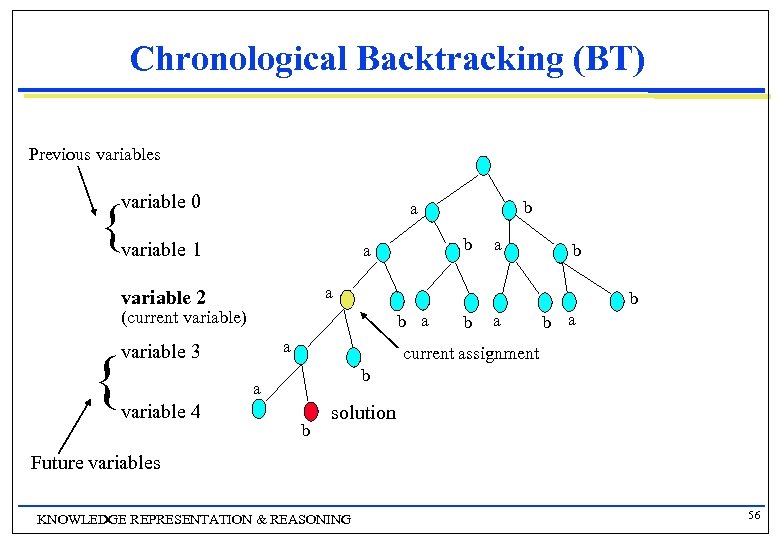
Chronological Backtracking (ΒΤ) Previous variable 0 { variable 1 a b (current variable) b a a variable 3 b a current assignment b a variable 4 b a variable 2 { b a b solution Future variables KNOWLEDGE REPRESENTATION & REASONING 56

Chronological Backtracking (ΒΤ) procedure CHRONOLOGICAL_BACKTRACKING (vars, doms, cons) solution BT (vars, Ø, doms, cons) function BT (unlabelled, compound_label, doms, cons) returns a solution or NIL if unlabelled = Ø then return compound_label else pick a variable x from unlabelled repeat pick a value v from Dx; delete v from Dx if compound_label + {(x, v)} violates no constraints then result BT(unlabelled - {x}, compound_label + {(x, v)}, doms, cons) if result NIL then return result end until Dx = Ø return NIL end KNOWLEDGE REPRESENTATION & REASONING 57
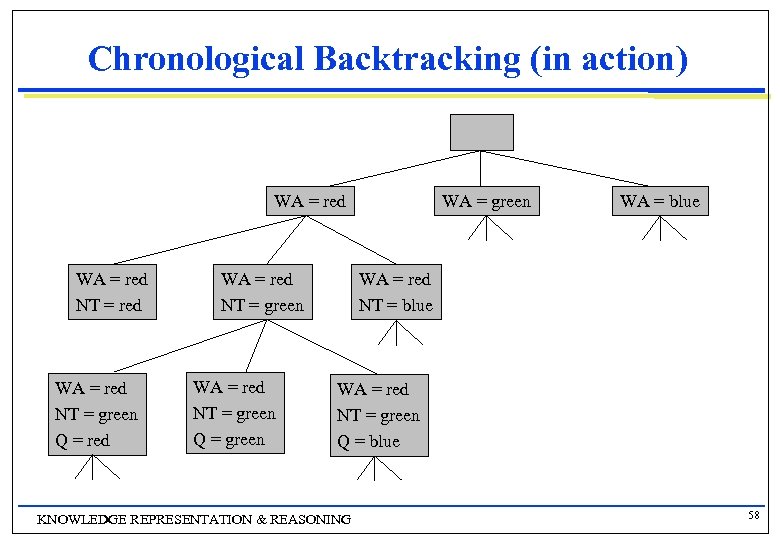
Chronological Backtracking (in action) WA = red NT = red WA = red NT = green Q = green WA = blue WA = red NT = green Q = blue KNOWLEDGE REPRESENTATION & REASONING 58
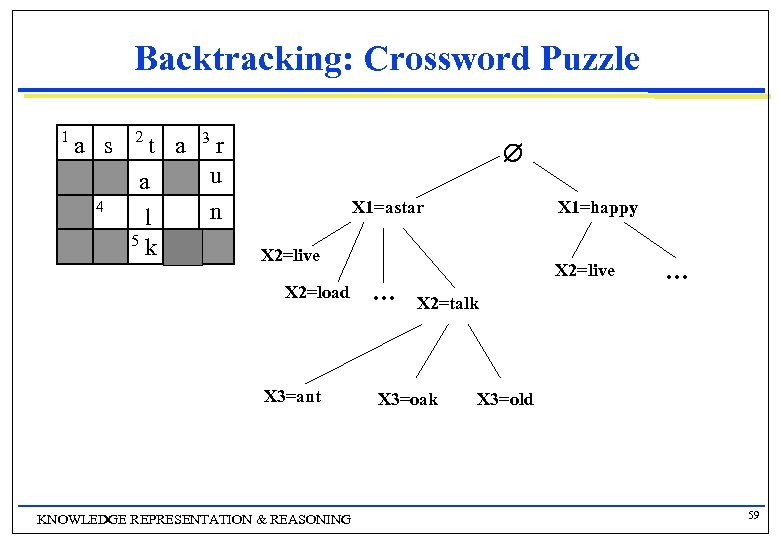
Backtracking: Crossword Puzzle 1 a s 4 2 t a 3 r u a n l 5 k X 1=astar X 1=happy X 2=live X 2=load X 3=ant KNOWLEDGE REPRESENTATION & REASONING … X 2=live … X 2=talk X 3=oak X 3=old 59

Chronological Backtracking (ΒΤ) Evaluation n Complete and Sound ? n g Yes and Yes n Time complexity: Ο(dne) g where d is the maximum domain size, n the number of variables, and e the number of constraints n Χώρος: Ο(nd) g the space required to store the domains of all variables n The complexities hold under the assumption that all constraint checks are performed in constant time and constraints are stored in constant space KNOWLEDGE REPRESENTATION & REASONING 60

GT & BT – Example 1 n Problem: X: : {1, 2}, Y: : {1, 2}, Z: : {1, 2} X = Y, X Z, Y > Z generate & test KNOWLEDGE REPRESENTATION & REASONING backtracking 61

GT & BT 4 -queen problem Q 1 1 2 3 4 Q 2 Q 3 Q 4 Place 4 queens so that no two queens are in attack. Qi: line number of queen in column i, for 1 i 4 Q 1, Q 2, Q 3, Q 4 Q 1 Q 2, Q 1 Q 3, Q 1 Q 4, Q 2 Q 3, Q 2 Q 4, Q 3 Q 4, Q 1 Q 2 -1, Q 1 Q 2+1, Q 1 Q 3 -2, Q 1 Q 3+2, Q 1 Q 4 -3, Q 1 Q 4+3, Q 2 Q 3 -1, Q 2 Q 3+1, Q 2 Q 4 -2, Q 2 Q 4+2, Q 3 Q 4 -1, Q 3 Q 4+1 KNOWLEDGE REPRESENTATION & REASONING 62

4 -queen problem first solution Q 1 Q 2 Q 3 Q 4 1 2 3 4 There is a total of 256 valuations GT algorithm will generate 64 valuations with Q 1=1; + + = 48 valuations with Q 1=2, 1 Q 2 3; 3 valuations with Q 1=2, Q 2=4, Q 3=1; 115 valuations to find first solution KNOWLEDGE REPRESENTATION & REASONING 63
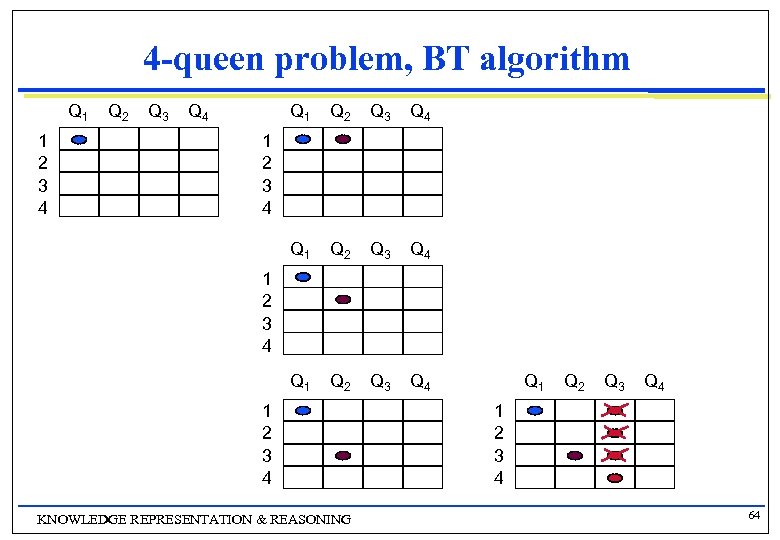
4 -queen problem, BT algorithm Q 1 Q 3 Q 1 Q 4 Q 2 Q 3 Q 4 Q 1 1 2 3 4 Q 2 Q 3 Q 4 1 2 3 4 KNOWLEDGE REPRESENTATION & REASONING Q 1 Q 2 Q 3 Q 4 1 2 3 4 64

Advantages n declarative nature with procedural capabilities (when needed) g n co-operative problem solving g n unified framework for integration of variety of special-purpose algorithms semantic foundation g g n focus on describing the problem to be solved, and choosing the algorithm to solve it amazingly clean and elegant languages roots in logic programming applications g proven success KNOWLEDGE REPRESENTATION & REASONING 65
Limitations NP-hard problems & tractability n unpredictable behaviour n ad-hoc modelling n too much expertise required n g new constraints, solvers, heuristics, modelling non-incremental (rescheduling) n awkward handling of optimization n g solvers tuned to finding first solution n weak solver collaboration g with OR engines for example KNOWLEDGE REPRESENTATION & REASONING 66

Useful Links n On-line guide to Constraint Programming g http: //kti. ms. mff. cuni. cz/%7 Ebartak/constraints/ n Constraints Archive g http: //www. cs. unh. edu/ccc/archive/ n CSPLib : a problem library for constraints g http: //4 c. ucc. ie/~tw/csplib/ n Course on Theory and Practice of Constraint Satisfaction g http: //www. cse. unl. edu/~choueiry/CSCE 990 -05/schedule. htm KNOWLEDGE REPRESENTATION & REASONING 67
256e21b5e51283a70b4d08f87db957ac.ppt