Constraint Propagation Constraint Propagation is

Constraint Propagation

Constraint Propagation … … is the process of determining how the possible values of one variable affect the possible values of other variables Constraint Propagation 2

Forward Checking After a variable X is assigned a value v, look at each unassigned variable Y that is connected to X by a constraint and deletes from Y’s domain any value that is inconsistent with v Constraint Propagation 3

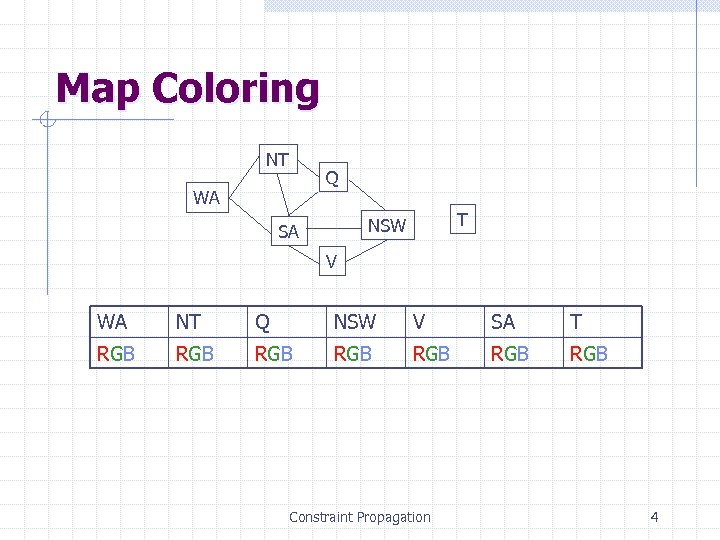Map Coloring NT Q WA T NSW SA V WA NT Q NSW V SA T RGB RGB Constraint Propagation 4

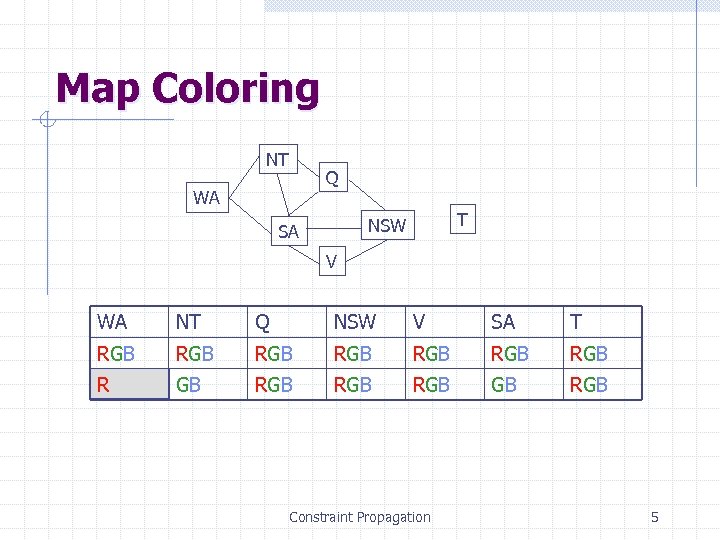Map Coloring NT Q WA T NSW SA V WA NT Q NSW V SA T RGB RGB R GB RGB RGB Constraint Propagation 5

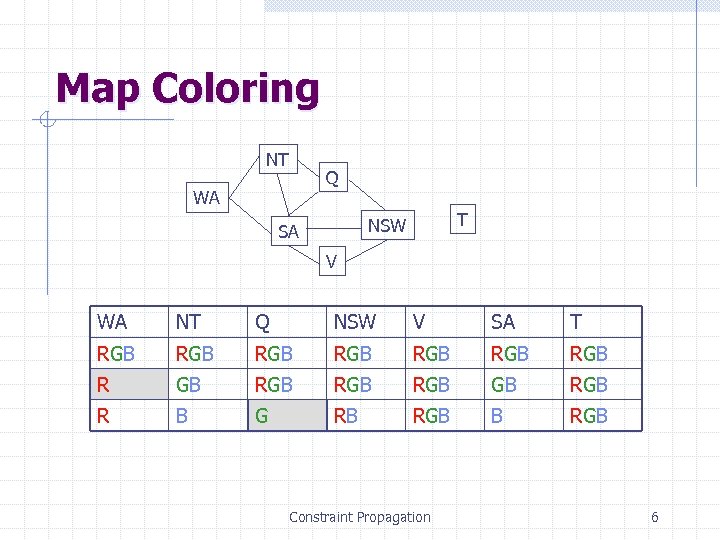Map Coloring NT Q WA T NSW SA V WA NT Q NSW V SA T RGB RGB R GB RGB RGB R B G RB RGB Constraint Propagation 6

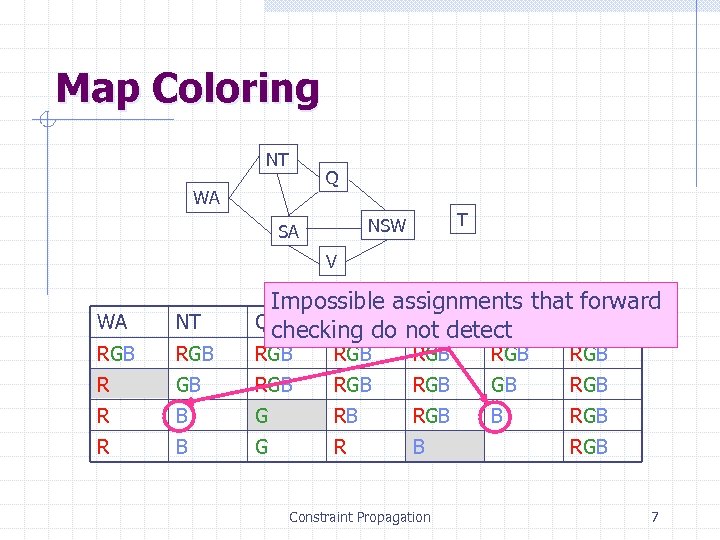Map Coloring NT Q WA T NSW SA V WA NT RGB R Impossible assignments that forward Q checking do not detect NSW V SA T RGB RGB RGB R B G RB RGB R B G R B Constraint Propagation RGB 7

Example: Street Puzzle 1 2 3 4 5 Ni = {English, Spaniard, Japanese, Italian, Norwegian} Ci = {Red, Green, White, Yellow, Blue} Di = {Tea, Coffee, Milk, Fruit-juice, Water} Ji = {Painter, Sculptor, Diplomat, Violonist, Doctor} Ai = {Dog, Snails, Fox, Horse, Zebra}

Example: Street Puzzle 2 3 4 1 5 Ni = {English, Spaniard, Japanese, Italian, Norwegian} Ci = {Red, Green, White, Yellow, Blue} Di = {Tea, Coffee, Milk, Fruit-juice, Water} Ji = {Painter, Sculptor, Diplomat, Violonist, Doctor} Ai = {Dog, Snails, Fox, Horse, Zebra} The Englishman lives in the Red house Who owns the Zebra? The Spaniard has a Dog Who drinks Water? The Japanese is a Painter The Italian drinks Tea The Norwegian lives in the first house on the left The owner of the Green house drinks Coffee The Green house is on the right of the White house The Sculptor breeds Snails The Diplomat lives in the Yellow house The owner of the middle house drinks Milk The Norwegian lives next door to the Blue house The Violonist drinks Fruit juice The Fox is in the house next to the Doctor’s The Horse is next to the Diplomat’s

Example: Task Scheduling T 1 T 2 T 4 T 3 T 1 T 2 T 4 must be done during T 3 be achieved before T 1 starts overlap with T 3 start after T 1 is complete • Are the constraints compatible? • Find the temporal relation between every two tasks

constraint propagation Constraint Propagation 11

Edge Labeling in Computer Vision Russell and Norvig: Chapter 24, pages 745 -749 Constraint Propagation 12

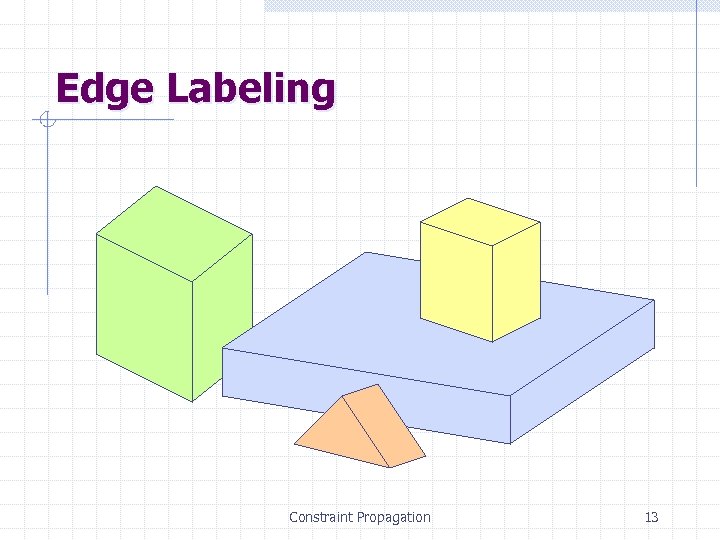Edge Labeling Constraint Propagation 13

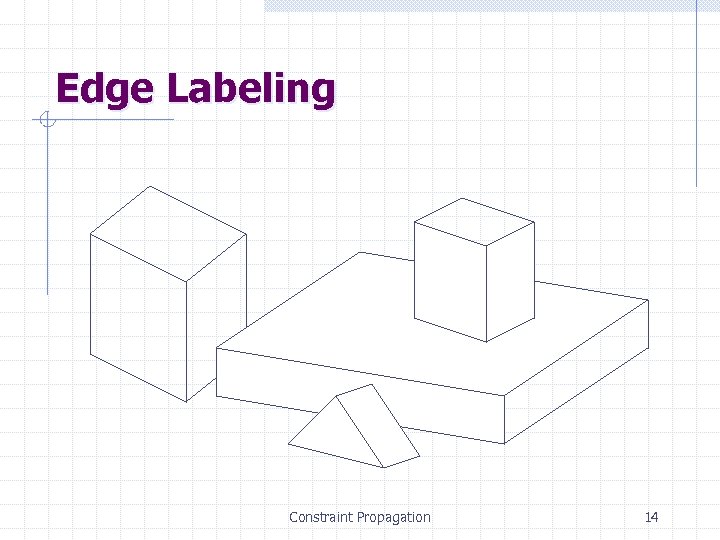Edge Labeling Constraint Propagation 14

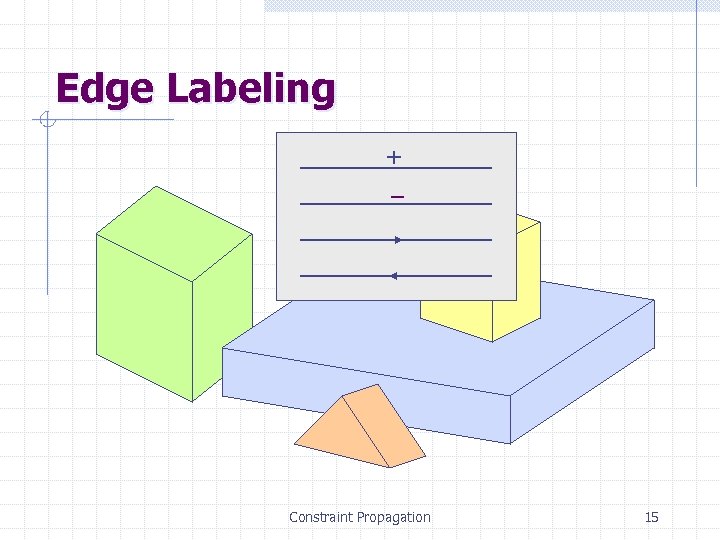Edge Labeling + – Constraint Propagation 15

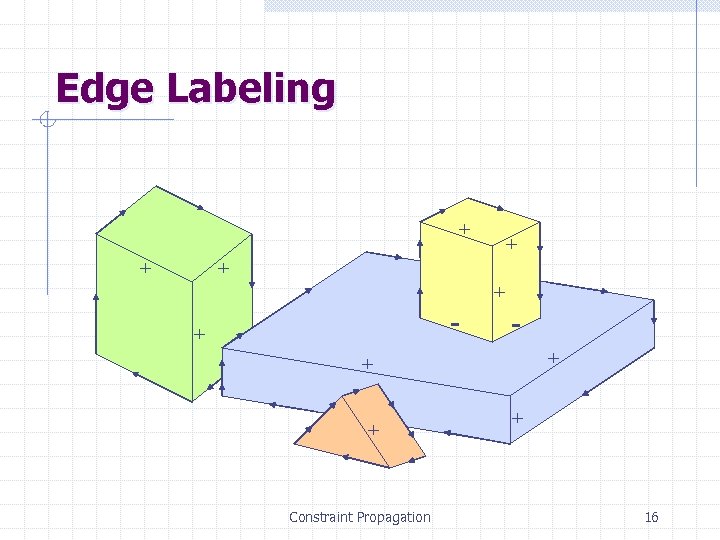Edge Labeling + + + - + + Constraint Propagation + 16

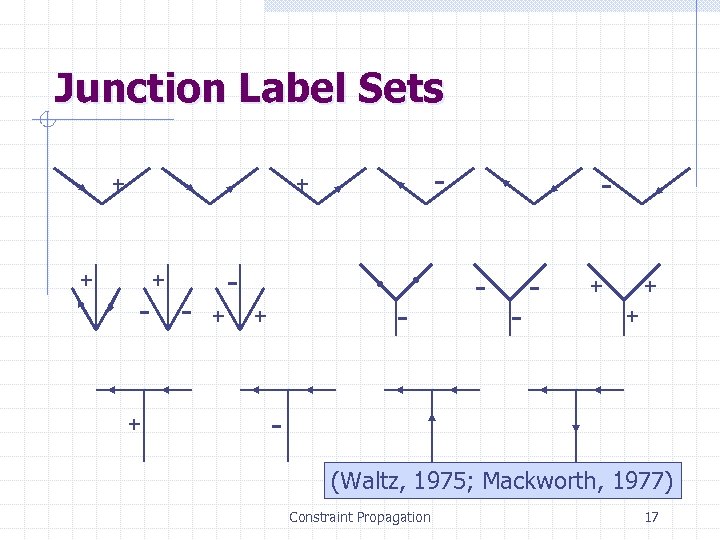Junction Label Sets + - + - - + + - - - + + + (Waltz, 1975; Mackworth, 1977) Constraint Propagation 17

Edge Labeling as a CSP A variable is associated with each junction The domain of a variable is the label set of the corresponding junction Each constraint imposes that the values given to two adjacent junctions give the same label to the joining edge Constraint Propagation 18

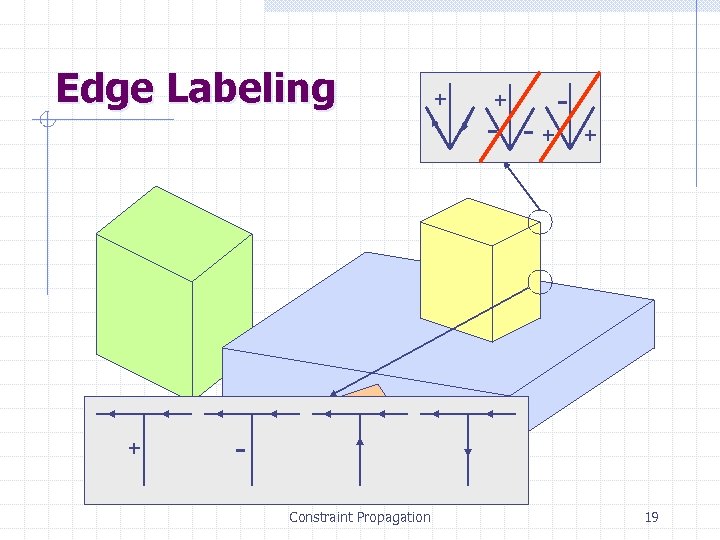Edge Labeling + + + - -+ + Constraint Propagation 19

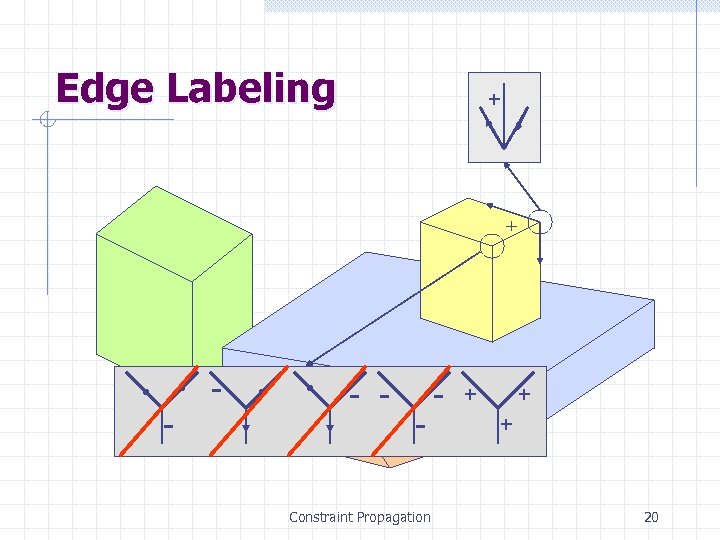Edge Labeling + + - - - Constraint Propagation - + + + 20

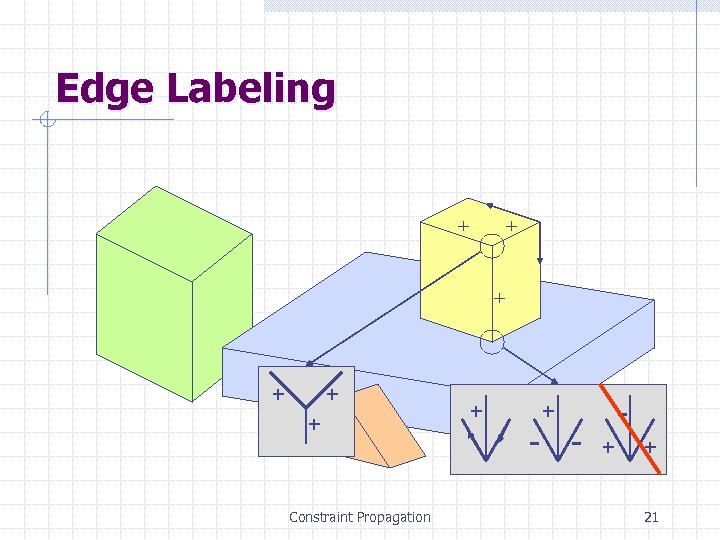Edge Labeling + + + Constraint Propagation + - - + + 21

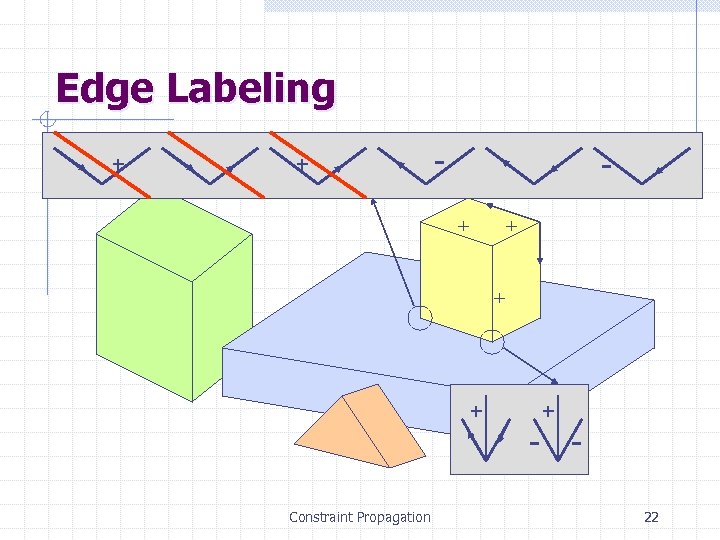Edge Labeling + + - + + + - Constraint Propagation 22

Removal of Arc Inconsistencies REMOVE-ARC-INCONSISTENCIES(J, K) removed false X label set of J Y label set of K For every label y in Y do n If there exists no label x in X such that the constraint (x, y) is satisfied then w Remove y from Y w If Y is empty then contradiction true w removed true Label set of K Y Return removed Constraint Propagation 23

CP Algorithm for Edge Labeling Associate with every junction its label set contradiction false Q stack of all junctions while Q is not empty and not contradiction do n J UNSTACK(Q) n For every junction K adjacent to J do w If REMOVE-ARC-INCONSISTENCIES(J, K) then n STACK(K, Q) (Waltz, 1975; Mackworth, 1977) Constraint Propagation 24

General CP for Binary Constraints Algorithm AC 3 contradiction false Q stack of all variables while Q is not empty and not contradiction do n X UNSTACK(Q) n For every variable Y adjacent to X do w If REMOVE-ARC-INCONSISTENCIES(X, Y) then n STACK(Y, Q) Constraint Propagation 25

General CP for Binary Constraints Algorithm AC 3 contradiction false Q stack of all variables while Q is not empty and not contradiction do n X UNSTACK(Q) n For every variable Y adjacent to X do w If REMOVE-ARC-INCONSISTENCY(X, Y) then n STACK(Y, Q) REMOVE-ARC-INCONSISTENCY(X, Y) removed false For every value y in the domain of Y do n If there exists no value x in the domain of X such that the constraints on (x, y) is satisfied then w Remove y from the domain of Y w If Y is empty then contradiction true w removed true Constraint Propagation 26 Return removed

Complexity Analysis of AC 3 n = number of variables d = number of values per variable s = maximum number of constraints on a pair of variables Each variables is inserted in Q up to d times REMOVE-ARC-INCONSISTENCY takes O(d 2) time CP takes O(n s d 3) time Constraint Propagation 27

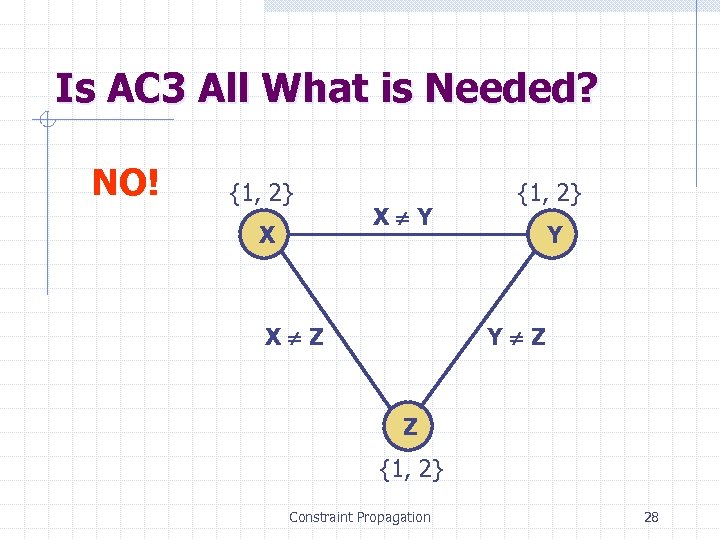Is AC 3 All What is Needed? NO! {1, 2} X X Y X Z {1, 2} Y Y Z Z {1, 2} Constraint Propagation 28

Solving a CSP Interweave constraint propagation, e. g. , • forward checking • AC 3 and backtracking + Take advantage of the CSP structure Constraint Propagation 29

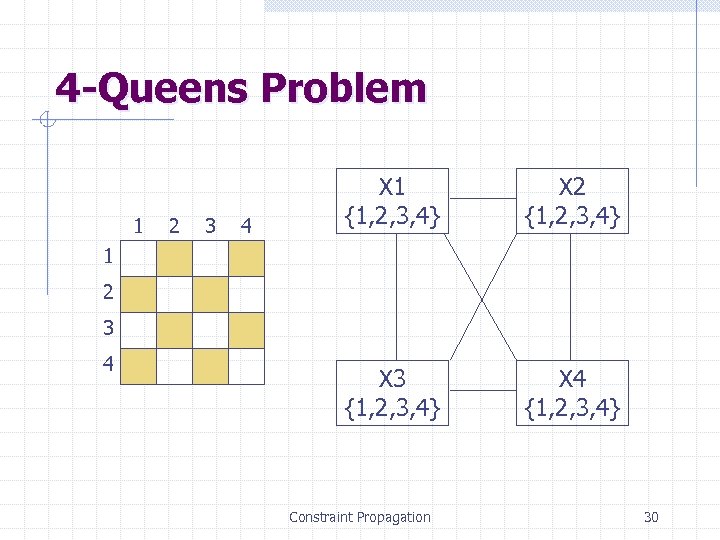4 -Queens Problem 1 2 3 4 X 1 {1, 2, 3, 4} X 2 {1, 2, 3, 4} X 3 {1, 2, 3, 4} X 4 {1, 2, 3, 4} 1 2 3 4 Constraint Propagation 30

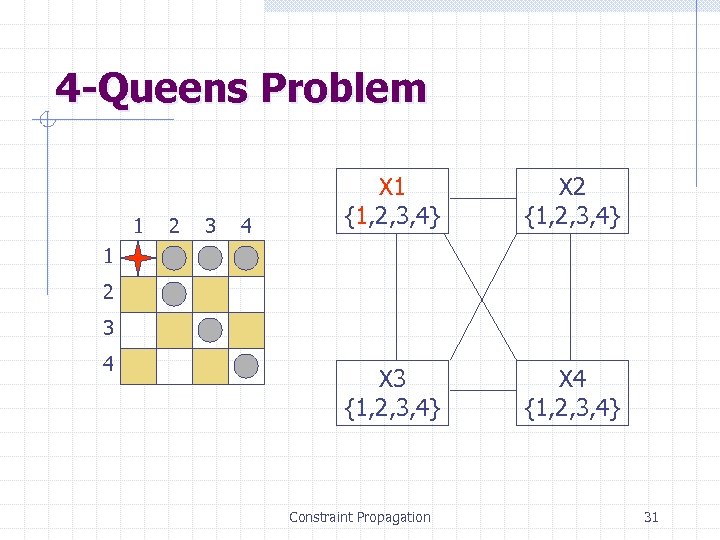4 -Queens Problem 1 2 3 4 X 1 {1, 2, 3, 4} X 2 {1, 2, 3, 4} X 3 {1, 2, 3, 4} X 4 {1, 2, 3, 4} 1 2 3 4 Constraint Propagation 31

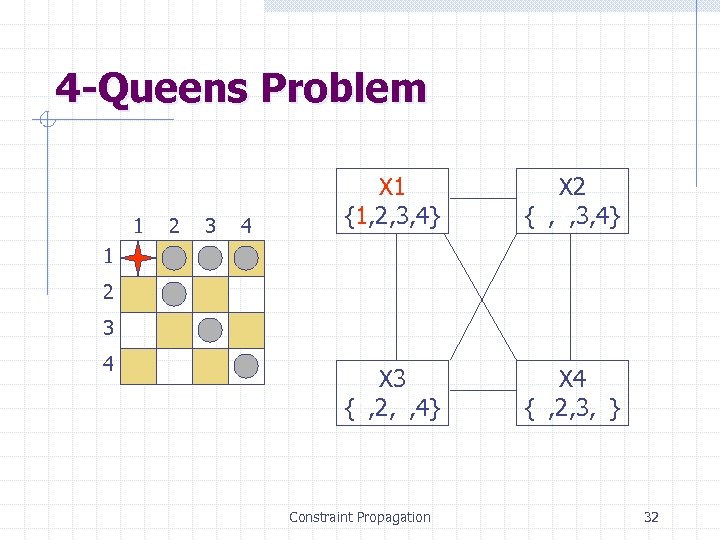4 -Queens Problem 1 2 3 4 X 1 {1, 2, 3, 4} X 2 {1, 2, 3, 4} X 3 {1, 2, 3, 4} X 4 {1, 2, 3, 4} 1 2 3 4 Constraint Propagation 32

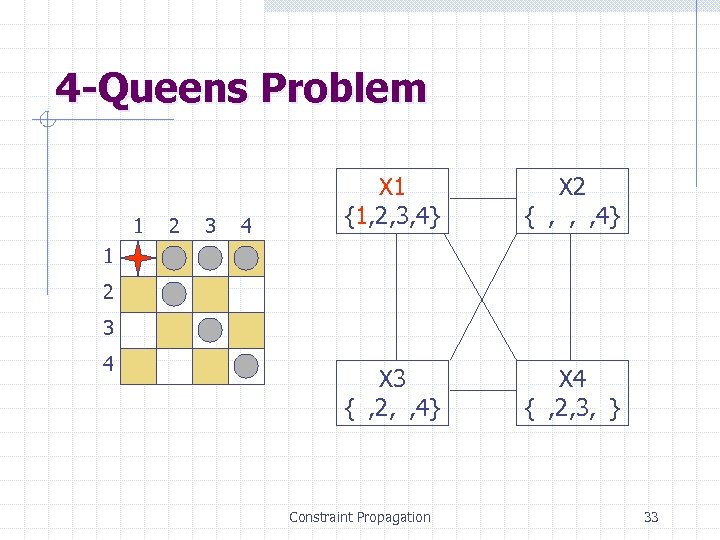4 -Queens Problem 1 2 3 4 X 1 {1, 2, 3, 4} X 2 {1, 2, 3, 4} X 3 {1, 2, 3, 4} X 4 {1, 2, 3, 4} 1 2 3 4 Constraint Propagation 33

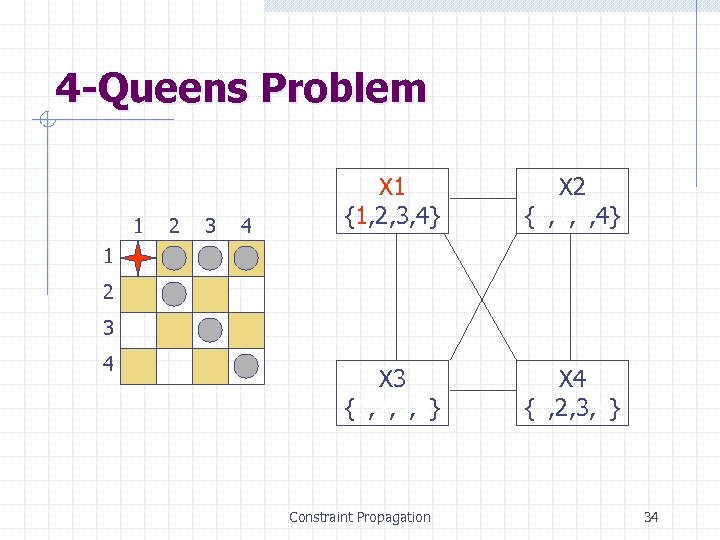4 -Queens Problem 1 2 3 4 X 1 {1, 2, 3, 4} X 2 {1, 2, 3, 4} X 3 {1, 2, 3, 4} X 4 {1, 2, 3, 4} 1 2 3 4 Constraint Propagation 34

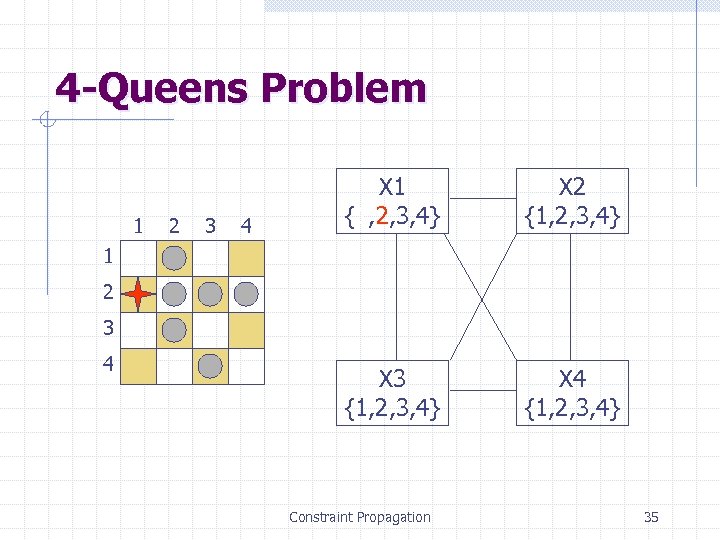4 -Queens Problem 1 2 3 4 X 1 {1, 2, 3, 4} X 2 {1, 2, 3, 4} X 3 {1, 2, 3, 4} X 4 {1, 2, 3, 4} 1 2 3 4 Constraint Propagation 35

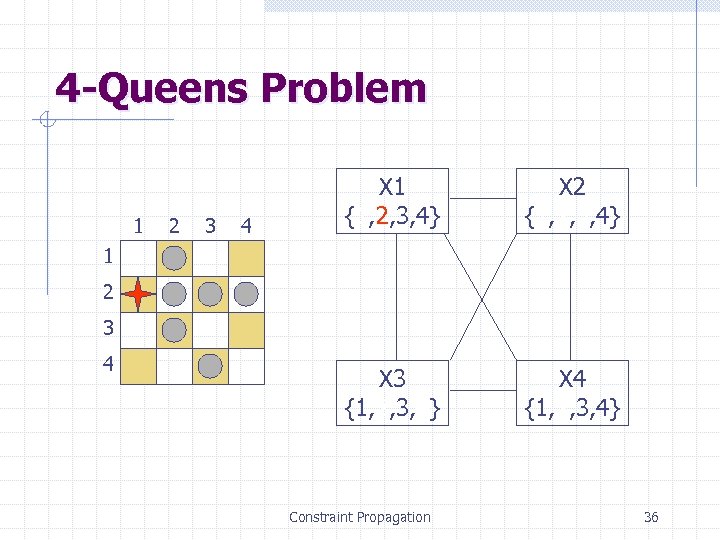4 -Queens Problem 1 2 3 4 X 1 {1, 2, 3, 4} X 2 {1, 2, 3, 4} X 3 {1, 2, 3, 4} X 4 {1, 2, 3, 4} 1 2 3 4 Constraint Propagation 36

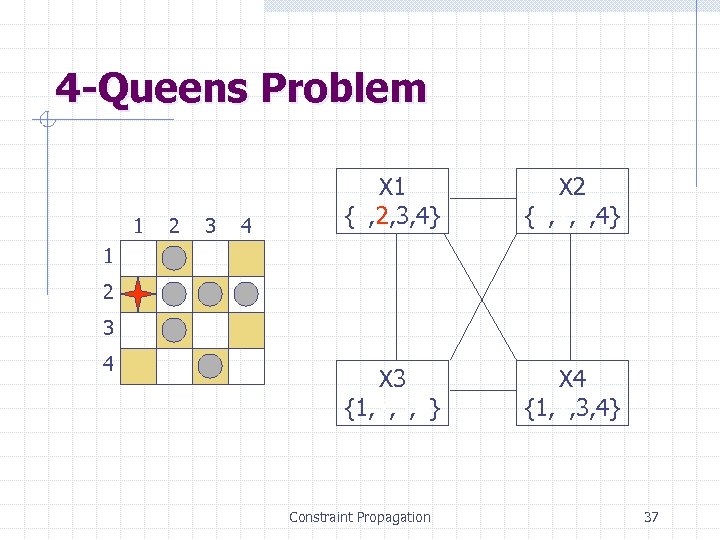4 -Queens Problem 1 2 3 4 X 1 {1, 2, 3, 4} X 2 {1, 2, 3, 4} X 3 {1, 2, 3, 4} X 4 {1, 2, 3, 4} 1 2 3 4 Constraint Propagation 37

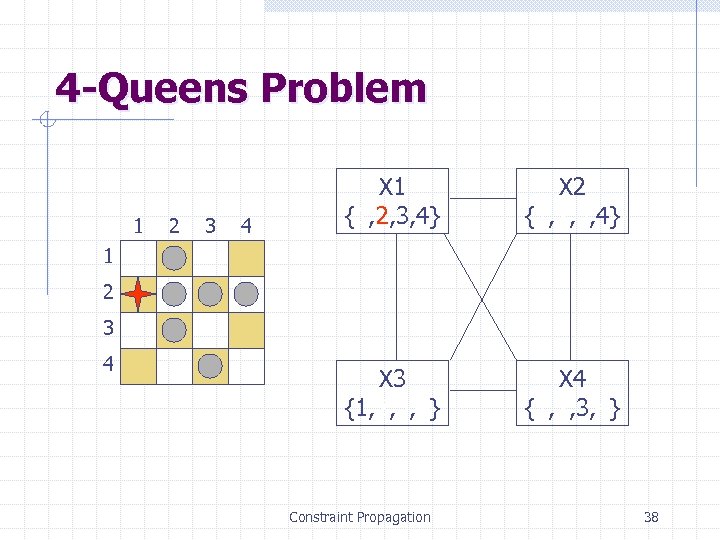4 -Queens Problem 1 2 3 4 X 1 {1, 2, 3, 4} X 2 {1, 2, 3, 4} X 3 {1, 2, 3, 4} X 4 {1, 2, 3, 4} 1 2 3 4 Constraint Propagation 38

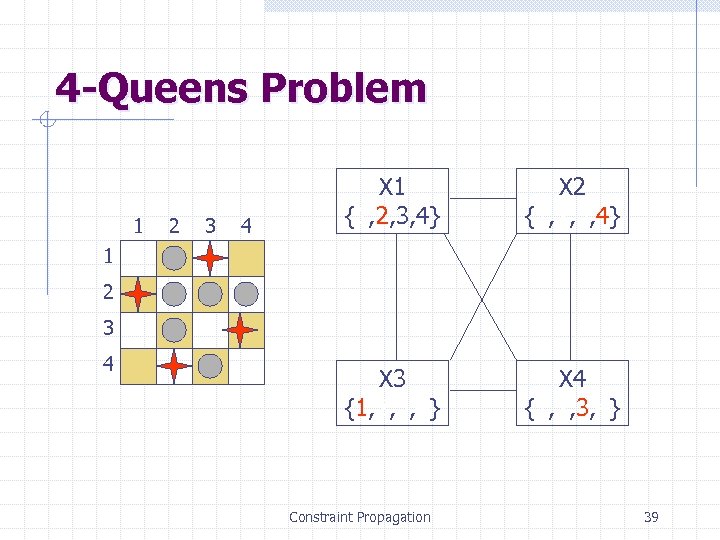4 -Queens Problem 1 2 3 4 X 1 {1, 2, 3, 4} X 2 {1, 2, 3, 4} X 3 {1, 2, 3, 4} X 4 {1, 2, 3, 4} 1 2 3 4 Constraint Propagation 39

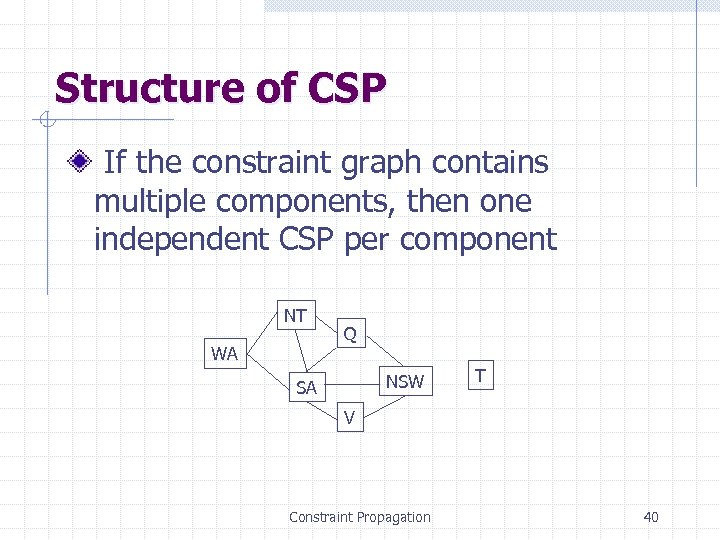Structure of CSP If the constraint graph contains multiple components, then one independent CSP per component NT WA Q NSW SA T V Constraint Propagation 40

Structure of CSP If the constraint graph contains multiple components, then one independent CSP per component If the constraint graph is a tree (no loop), then the CSP can be solved efficiently Constraint Propagation 41

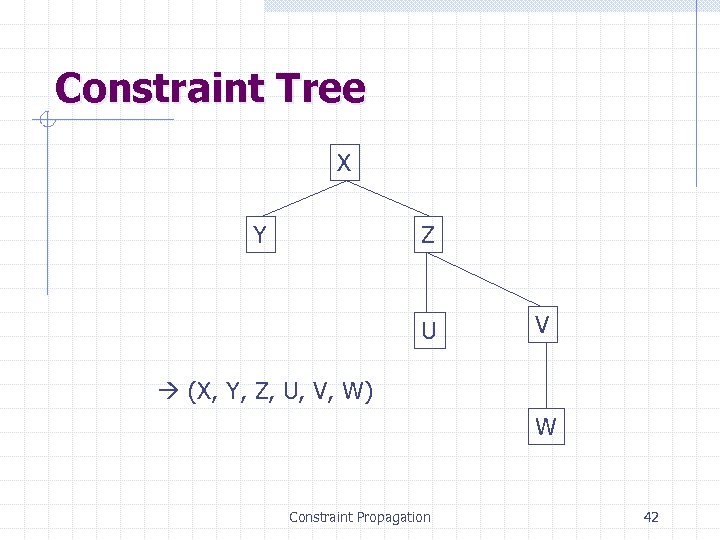Constraint Tree X Y Z U V (X, Y, Z, U, V, W) W Constraint Propagation 42

Constraint Tree Order the variables from the root to the leaves (X 1, X 2, …, Xn) For j = n, n-1, …, 2 do REMOVE-ARC-INCONSISTENCY(Xj, Xi) where Xi is the parent of Xj Assign any legal value to X 1 For j = 2, …, n do n assign any value to Xj consistent with the value assigned to Xi, where Xi is the parent of Xj Constraint Propagation 43

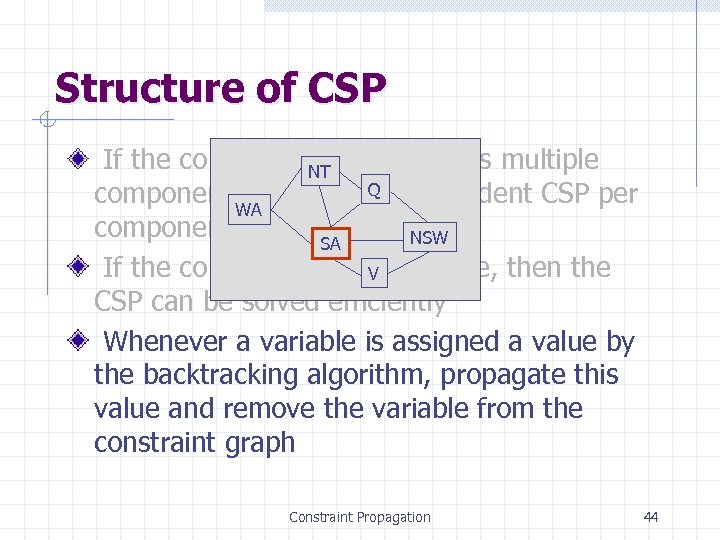Structure of CSP If the constraint NT graph contains multiple components, then one. Qindependent CSP per WA component NSW SA If the constraint graph is a tree, then the V CSP can be solved efficiently Whenever a variable is assigned a value by the backtracking algorithm, propagate this value and remove the variable from the constraint graph Constraint Propagation 44

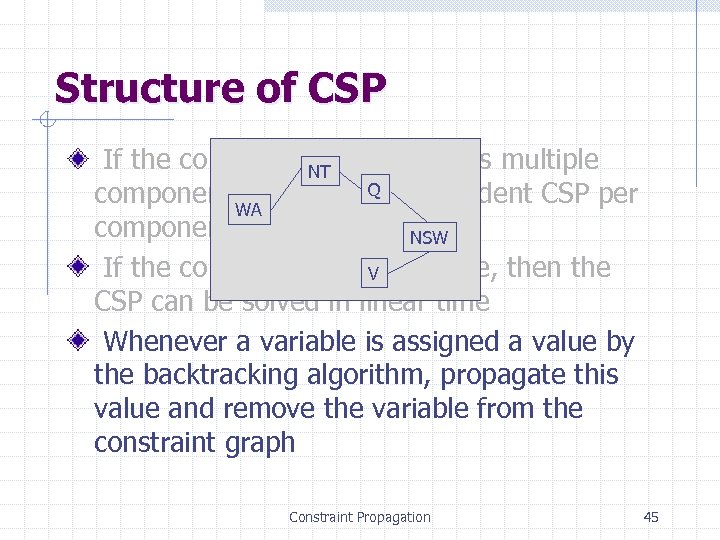Structure of CSP If the constraint NT graph contains multiple components, then one. Qindependent CSP per WA component NSW If the constraint graph is a tree, then the V CSP can be solved in linear time Whenever a variable is assigned a value by the backtracking algorithm, propagate this value and remove the variable from the constraint graph Constraint Propagation 45

Backtracking Algorithm CSP-BACKTRACKING({}) CSP-BACKTRACKING(a) n n partial assignment of variables If a is complete then return a X select unassigned variable D select an ordering for the domain of X For each value v in D do w If v is consistent with a then n n Add (X= v) to a result CSP-BACKTRACKING(a) If result failure then return result Return failure

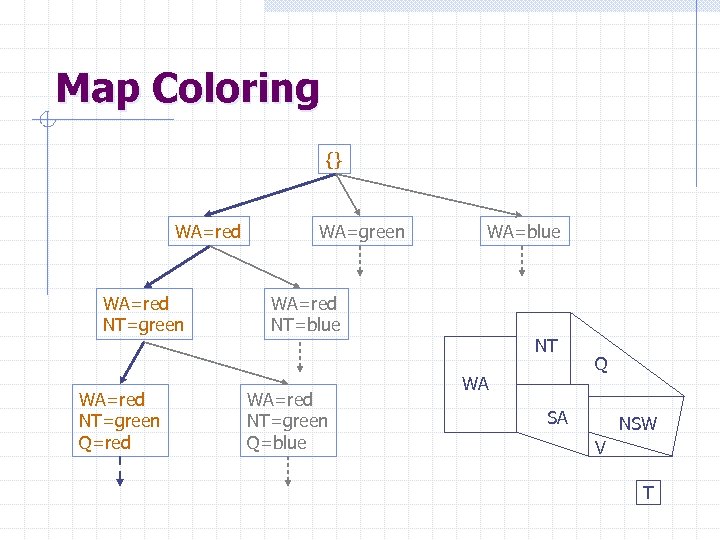Map Coloring {} WA=red NT=green Q=red WA=green WA=blue WA=red NT=green Q=blue NT WA Q SA NSW V T

Questions 1. Which variable X should be assigned a value next? 2. In which order should its domain D be sorted?

Questions 1. Which variable X should be assigned a value next? 2. In which order should its domain D be sorted? 3. What are the implications of a partial assignment for yet unassigned variables? ( Constraint Propagation -- see next class)

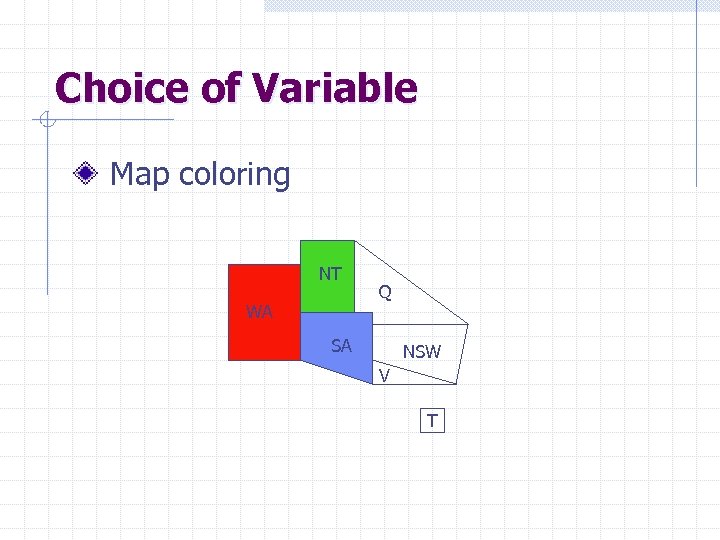Choice of Variable Map coloring NT WA Q SA NSW V T

Choice of Variable Most-constrained-variable heuristic: Select a variable with the fewest remaining values

Choice of Variable NT WA Q SA NSW V T Most-constraining-variable heuristic: Select the variable that is involved in the largest number of constraints on other unassigned variables

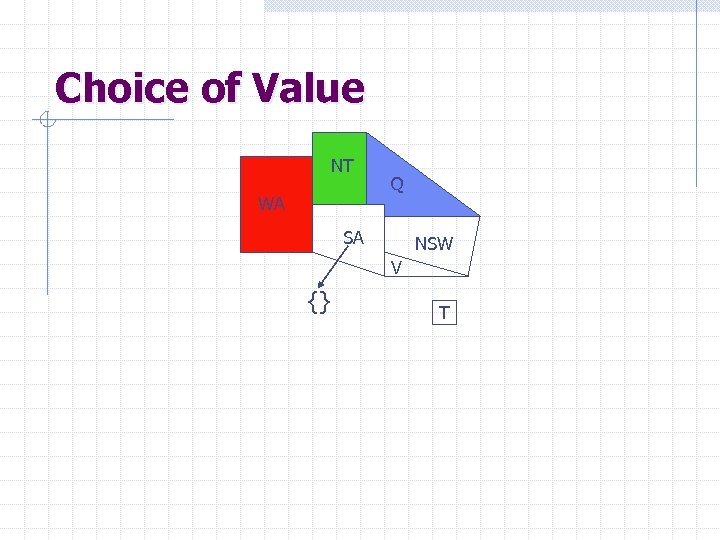Choice of Value NT WA Q SA NSW V {} T

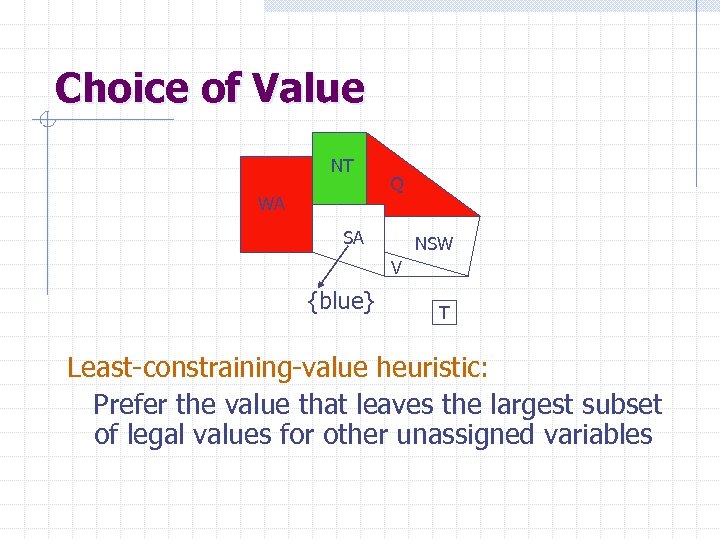Choice of Value NT WA Q SA NSW V {blue} T Least-constraining-value heuristic: Prefer the value that leaves the largest subset of legal values for other unassigned variables

Local Search for CSP 1 2 3 3 2 2 3 2 0 2 2 2 Pick initial complete assignment (at random) Repeat • Pick a conflicted variable var (at random) • Set the new value of var to minimize the number of conflicts • If the new assignment is not conflicting then return it (min-conflicts heuristics)

Remark Local search with min-conflict heuristic works extremely well for million-queen problems The reason: Solutions are densely distributed in the O(nn) space, which means that on the average a solution is a few steps away from a randomly picked assignment

Applications CSP techniques allow solving very complex problems Numerous applications, e. g. : n n n Crew assignments to flights Management of transportation fleet Flight/rail schedules Task scheduling in port operations Design Brain surgery

Stereotaxic Brain Surgery

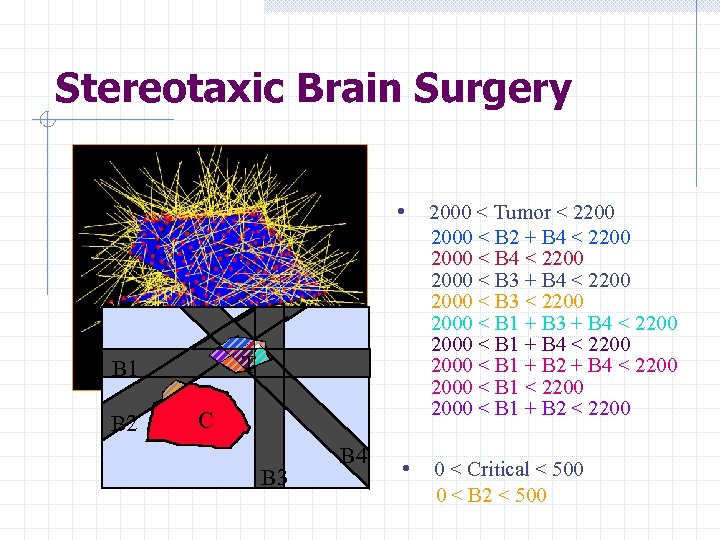Stereotaxic Brain Surgery • • 0 < Critical < 500 0 < B 2 < 500 T B 1 B 2 2000 < Tumor < 2200 2000 < B 2 + B 4 < 2200 2000 < B 3 < 2200 2000 < B 1 + B 3 + B 4 < 2200 2000 < B 1 + B 2 < 2200 C B 3 B 4

Constraint Programming “Constraint programming represents one of the closest approaches computer science has yet made to the Holy Grail of programming: the user states the problem, the computer solves it. ” Eugene C. Freuder, Constraints, April 1997

Over-Constrained Problems Weaken an over-constrained problem by: n n Enlarging the domain of a variable Loosening a constraint Removing a variable Removing a constraint Constraint Propagation 61

Non-Binary Constraints So far, all constraints have been binary (two variables) or unary (one variable) Constraints with more than 2 variables would be difficult to propagate Theoretically, one can reduce a constraint with k>2 variables to a set of binary constraints by introducing additional variables Constraint Propagation 62

When to Use CSP Techniques? When the problem can be expressed by a set of variables with constraints on their values When constraints are relatively simple (e. g. , binary) When constraints propagate well (AC 3 eliminates many values) When the solutions are “densely” distributed in the space of possible assignments Constraint Propagation 63

Summary Forward checking Constraint propagation Edge labeling in Computer Vision Interweaving CP and backtracking Exploiting CSP structure Weakening over-constrained CSP Constraint Propagation 64

Game Playing

Games as search problems Chess, Go Simulation of war (war game) 스타크래프트의 전투 Claude Shannon, Alan Turing Chess program (1950년대) Constraint Propagation 66

Contingency problems The opponent introduces uncertainty 마이티에서는 co-work이 필요 고스톱에서는 co-work방지가 필요 Hard to solve in chess, 35100 possible nodes, 1040 different legal positions Time limits how to make the best use of time to reach good decisions Pruning, heuristic evaluation function Constraint Propagation 67

Perfect decisions in two person games The initial state, A set of operators, A terminal test, A utility function (payoff function) Mini-max algorithm, Negmax algorithms Constraint Propagation 68

Mini-max algorithm (AND-OR tree) Constraint Propagation 69

상대방의 관점 Constraint Propagation 70

Negmax Knuth and Moore (1975) F(n) = f(n), if n has no successors F(n) = max{-F(n 1), …, -F(nk)}, if n has successors n 1, …, nk Constraint Propagation 71

The Negmax formalism Constraint Propagation 72

Imperfect Decisions utility function evaluation terminal test cutoff test Evaluation function : : : an estimate of the utility of the game from a given position Chess material value (장기도 유사) Weighted linear function w 1 f 1+w 2 f 2+…. +wnfn Constraint Propagation 73

Cutting off search To set a fixed depth limit, so that the cutoff test succeeds for all nodes at or below depth d iterative deepening until time runs out 위험이 있을 수 있다 Quiescent posiiton : : : unlikely to exhibit wild swings in value in near future Quiescent search : : Non-quiescent search extra search to find quiescent position Horizon problem Constraint Propagation 74

Alpha-beta pruning Eliminate unnecessary evaluations Pruning Constraint Propagation 75

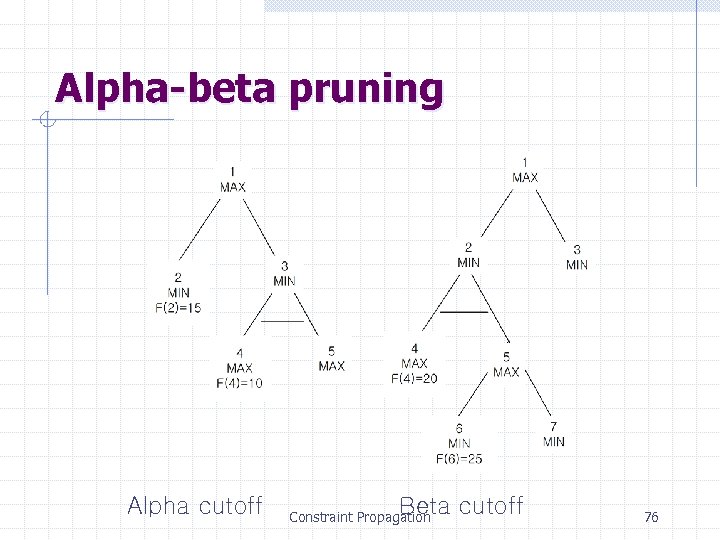Alpha-beta pruning Alpha cutoff Beta cutoff Constraint Propagation 76

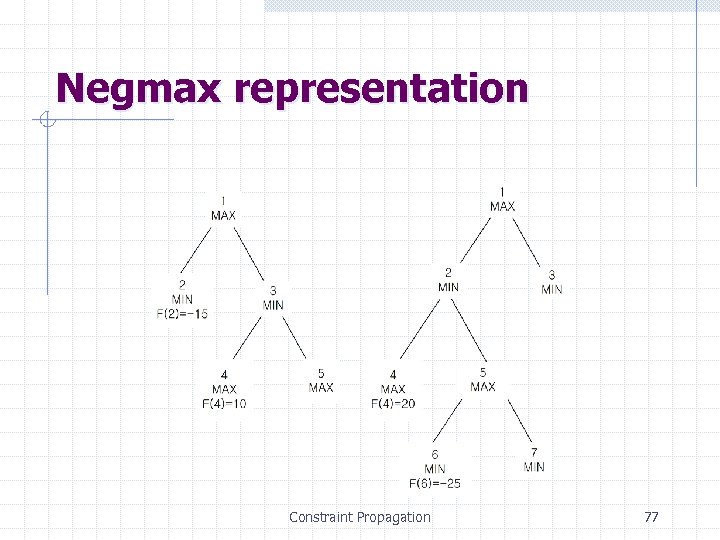Negmax representation Constraint Propagation 77

Example Constraint Propagation 78

Games with Chance nodes expected value Backgammon, 윷놀이 Expectimax value Constraint Propagation 79

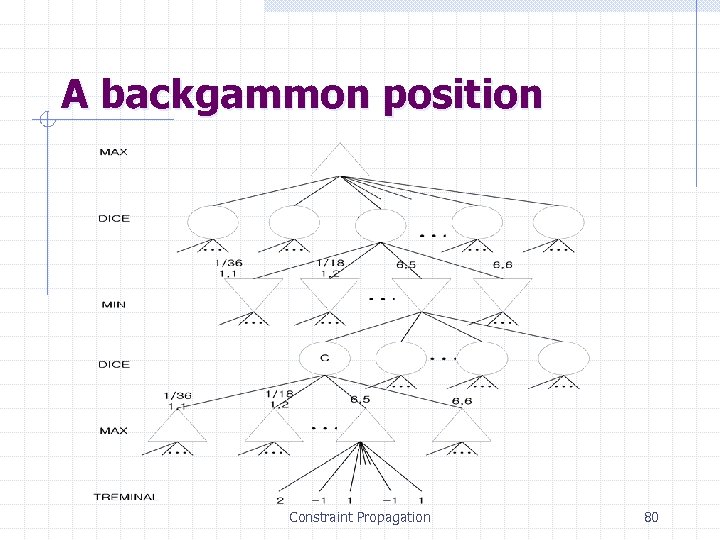A backgammon position Constraint Propagation 80

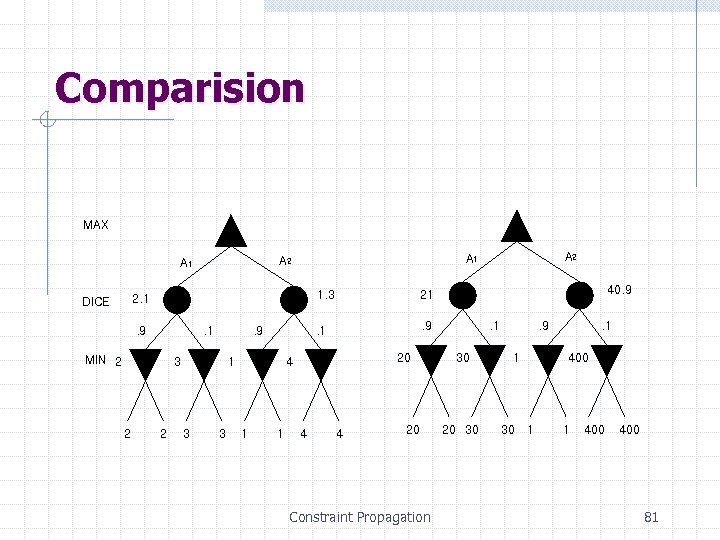Comparision MAX 1. 3 . 9 . 1 MIN 2 . 9 3 2 2 1 3 3 . 9 20 4 1 1 4 40. 9 21 . 1 2. 1 DICE A 2 A 1 4 20 Constraint Propagation . 1 30 20 30 . 9 1 30 . 1 400 1 1 400 81