Constraint Programming Planning and Scheduling with Time and

Constraint Programming, Planning and Scheduling with Time and Resource Constraints Claude Le Pape - ILOG S. A. Disclaimer: not (at all) a complete overview of the field! 1 C. Le Pape

Outline • Constraint Programming • Constraint-Based Scheduling • Cooperative Problem-Solving 2 C. Le Pape

Constraint Programming • Explicit problem definition • Separation between problem definition and problem solving • Systematic deduction of the consequences of made decisions (constraint propagation) Partial constraint propagation è development of heuristic search algorithms to generate and optimize solutions • Incremental constraint propagation (with global fix point semantics) • Localized definition of the constraint propagation process (each constraint propagates independently of other constraints) è many different types of constraints viewed as as many sub-problems 3 C. Le Pape

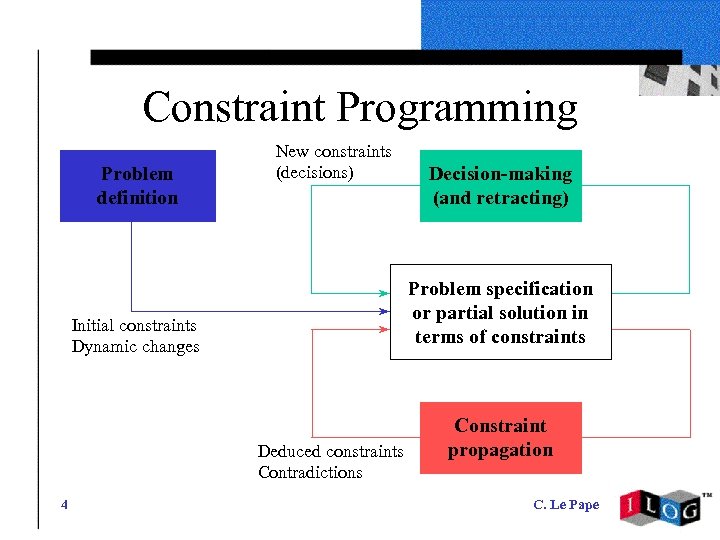Constraint Programming Problem definition New constraints (decisions) Problem specification or partial solution in terms of constraints Initial constraints Dynamic changes Deduced constraints Contradictions 4 Decision-making (and retracting) Constraint propagation C. Le Pape

Example: Propagation Variables: x in [1. . 3] y in [1. . 3] z in [1. . 3] Constraints: x - y = 1 y < z x != z x - y = 1 y < z x in [2. . 3] y in [1. . 2] z in [2. . 3] x != z 5 x in [2. . 3] y in [1. . 2] z in [1. . 3] x in [2. . 3] y in [1. . 2] z in [2. . 3] C. Le Pape

Example: Decision-Making Variables: x in [2. . 3] y in [1. . 2] z in [2. . 3] y = 2 Constraints: x - y = 1 y < z x != z x = 3 y = 2 z = 3 FAILURE Backtrack y = 1 6 x = 2 y = 1 z = 3 C. Le Pape

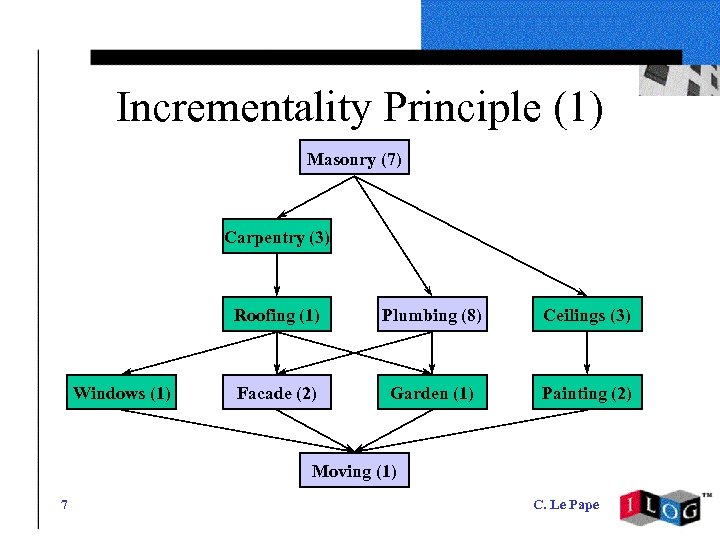Incrementality Principle (1) Masonry (7) Carpentry (3) Roofing (1) Windows (1) Plumbing (8) Ceilings (3) Facade (2) Garden (1) Painting (2) Moving (1) 7 C. Le Pape

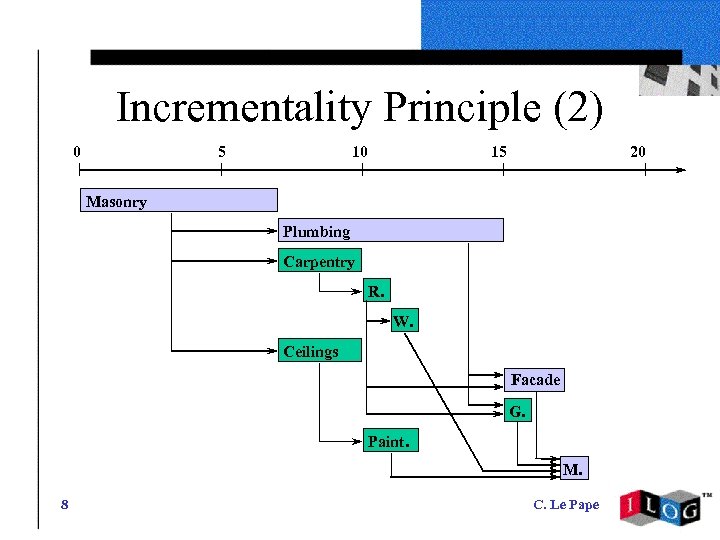Incrementality Principle (2) 0 5 10 15 20 Masonry Plumbing Carpentry R. W. Ceilings Facade G. Paint. M. 8 C. Le Pape

Incrementality Principle (3) • "Plumber" = "Roofer" • Solution: Order "Plumbing" and "Roofing" • Heuristic choice For example, "Plumbing" before "Roofing" 9 C. Le Pape

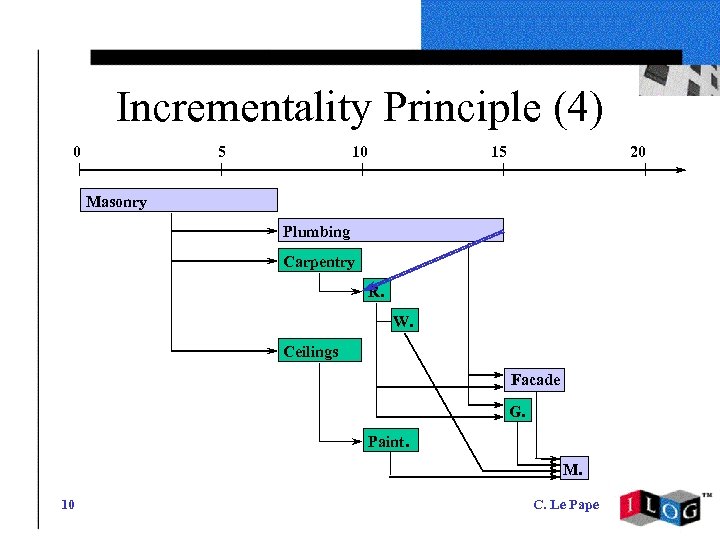Incrementality Principle (4) 0 5 10 15 20 Masonry Plumbing Carpentry R. W. Ceilings Facade G. Paint. M. 10 C. Le Pape

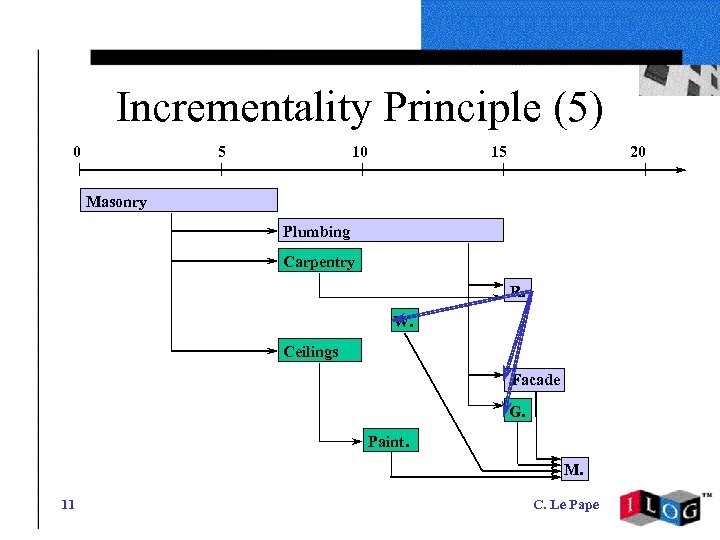Incrementality Principle (5) 0 5 10 15 20 Masonry Plumbing Carpentry R. W. Ceilings Facade G. Paint. M. 11 C. Le Pape

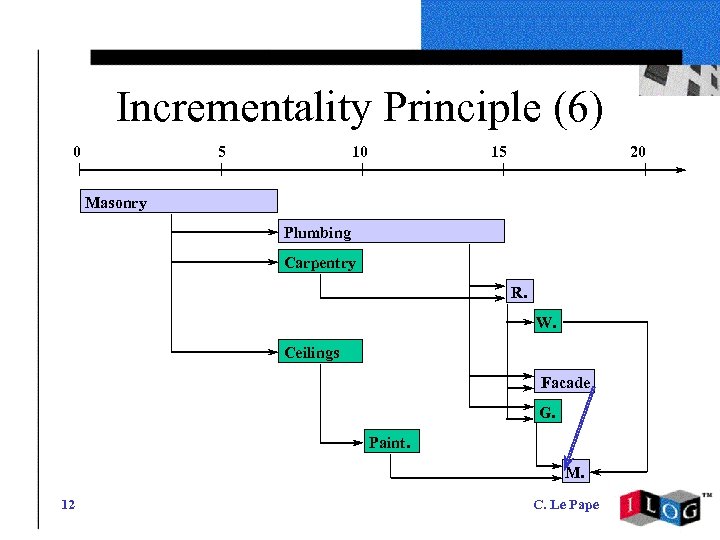Incrementality Principle (6) 0 5 10 15 20 Masonry Plumbing Carpentry R. W. Ceilings Facade G. Paint. M. 12 C. Le Pape

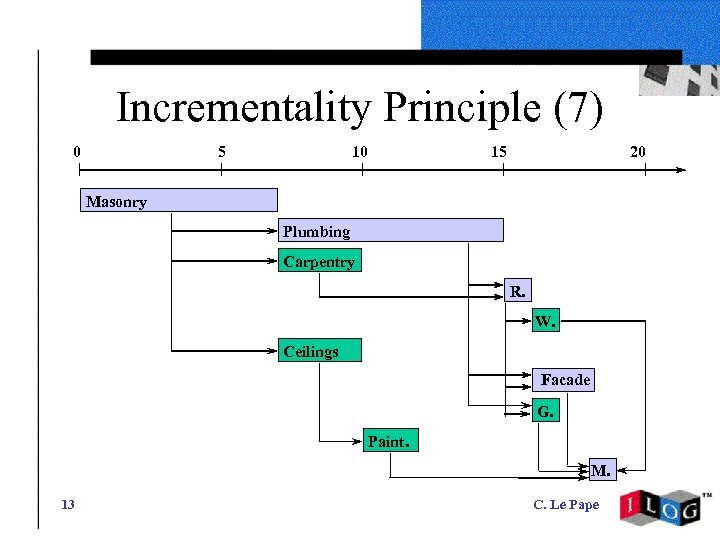Incrementality Principle (7) 0 5 10 15 20 Masonry Plumbing Carpentry R. W. Ceilings Facade G. Paint. M. 13 C. Le Pape

Incrementality Principle (8) Constraint propagation consists in incrementally updating characteristics of a partial problem solution when an additional constraint is added These characteristics may be: – indicators of contradictions – domains of variables (relational propagation) – the overall set of constraints (logic/algebraic propagation) 14 C. Le Pape

Incrementality Principle (9) Particular case: arc-consistency A constraint propagation technique enforces arc-consistency if and only if when propagation stops the following statement holds: for every constraint c(v 1. . . vn) for every variable vi for every value vali in the domain of vi there are values val 1. . . vali-1 vali+1. . . valn in the domains of v 1. . . vi-1 vi+1. . . vn such that val 1. . . vali-1 vali+1. . . valn satisfy c Considering a constraint as a sub-problem, arc-consistency consists of removing all the values that do not belong to any solution of the sub-problem 15 C. Le Pape

Locality Principle (1) • Each constraint (or constraint type) "includes" all the information necessary to enable its propagation and, in particular, to determine whether it is satisfied or not as soon as all its variables are instantiated • The constraint propagation methods associated with a constraint (or constraint type) are a priori independent of the methods associated with other constraints 16 C. Le Pape

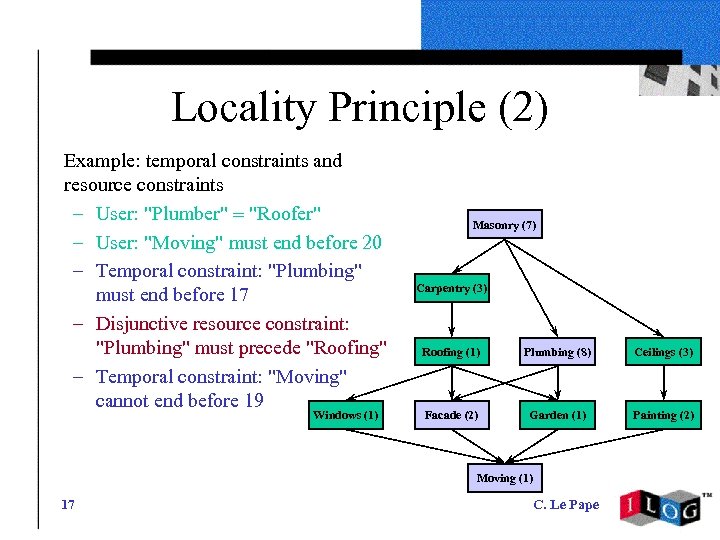Locality Principle (2) Example: temporal constraints and resource constraints – User: "Plumber" = "Roofer" – User: "Moving" must end before 20 – Temporal constraint: "Plumbing" must end before 17 – Disjunctive resource constraint: "Plumbing" must precede "Roofing" – Temporal constraint: "Moving" cannot end before 19 Windows (1) Masonry (7) Carpentry (3) Roofing (1) Plumbing (8) Ceilings (3) Facade (2) Garden (1) Painting (2) Moving (1) 17 C. Le Pape

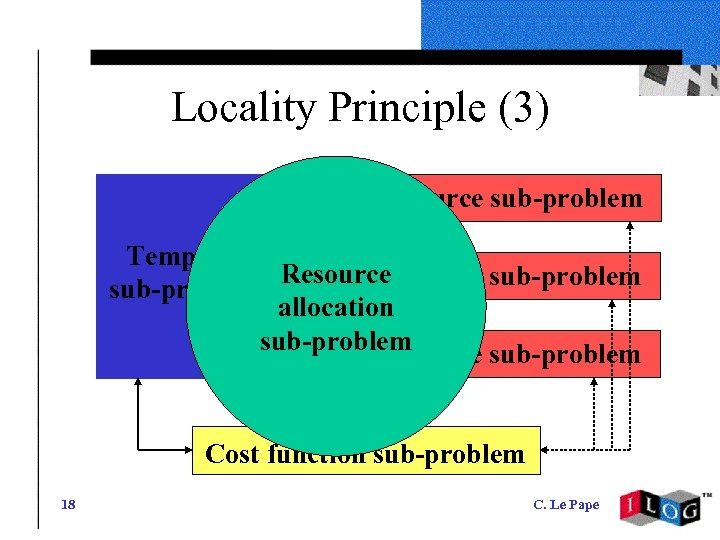Locality Principle (3) Resource sub-problem Temporal Resource sub-problem allocation sub-problem Resource sub-problem Cost function sub-problem 18 C. Le Pape

Outline • Constraint Programming • Constraint-Based Scheduling • Cooperative Problem-Solving 19 C. Le Pape

Outline • Constraint Programming • Constraint-Based Scheduling – Scheduling Problems – Propagation of Temporal Constraints – Propagation of Resource Constraints – Examples of Applications • Cooperative Problem-Solving 20 C. Le Pape

Scheduling Problems "Scheduling is the allocation of resources over time to perform a collection of tasks" [Baker 74] – Pure scheduling problems: assignment of start and end times to activities (each activity requires given resources with given capacities) – Pure resource allocation problems: assignment of resources to activities (the start and end times of each activity are given) – Joint scheduling and resource allocation problems: assignment of resources and start and end times to activities 21 C. Le Pape

Scheduling Problems • Transportation – Traffic scheduling and control (aircrafts, buses, trains, trucks) – Loading and unloading (aircrafts, ships, trucks) – Crew rostering • Production and maintenance • Manpower planning and timetabling (shifts, courses, exams) • Project or mission scheduling • Network planning and routing • Computer or printer job scheduling • Mixture planning, rack configuration, textile cutting, . . . 22 C. Le Pape

Variety of Scheduling Problems • • • 23 Activities Resources Constraints Optimization criteria Problem size Time available to make a decision C. Le Pape

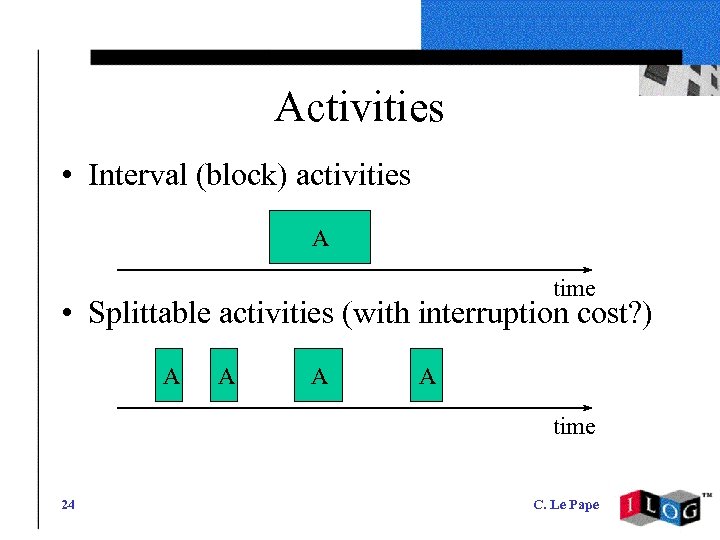Activities • Interval (block) activities A time • Splittable activities (with interruption cost? ) A A time 24 C. Le Pape

Resources • Unary resources – one person – one machine • Discrete resources – a group of people with the same capabilities • State resources – an oven with different possible temperatures • Energetic resources – a limited number of human-days each week • Required, provided, consumed or produced by activities 25 C. Le Pape

Constraints • Temporal constraints – Fixed or variable durations – Precedence constraints – Minimal and maximal delays • Resource constraints – Fixed capacity – Variable capacity (time versus capacity tradeoffs) – Variable capacity over time • Specific constraints 26 C. Le Pape

Capacity Constraints • Periods during which a resource is not fully available – Maintenance periods – Vacations – Forbidden states (at night) • Periods during which some minimal amount must be required or provided 27 C. Le Pape

Optional/Variable Requirements • Optional activities – Resource alternatives – Sub-contracts 28 C. Le Pape

Optional/Variable Requirements • Time versus capacity tradeoffs 2 people during 3 days or 3 people during 2 days 29 C. Le Pape

Optional/Variable Requirements • Variable requirement over time Example: 8 person-days with either 2 or 3 people at any time 30 C. Le Pape

Transition Times • Tool setup between two tasks on the same machine • State change (oven temperature, color used in a painting shop) • Cleaning 31 C. Le Pape

Percentage Constraints • a% of activity A on resource RA must be done before (or after): – B starts – B ends – b% of activity B on resource RB are done • Often complements variable requirements over time 32 C. Le Pape

Synchronization Constraints • When A executes, B requires (at least, at most) c 1 units of resource R • When A does not execute, B requires (at least, at most) c 2 units of resource R 33 C. Le Pape

Optimization Criteria • No optimization criterion • A well-defined criterion – – Project makespan Number of activities performed within given delays Maximal or average tardiness or earliness Peak or average resource utilization • A combination of well-defined criteria • Preferences (soft constraints) • Optimization versus robustness 34 C. Le Pape

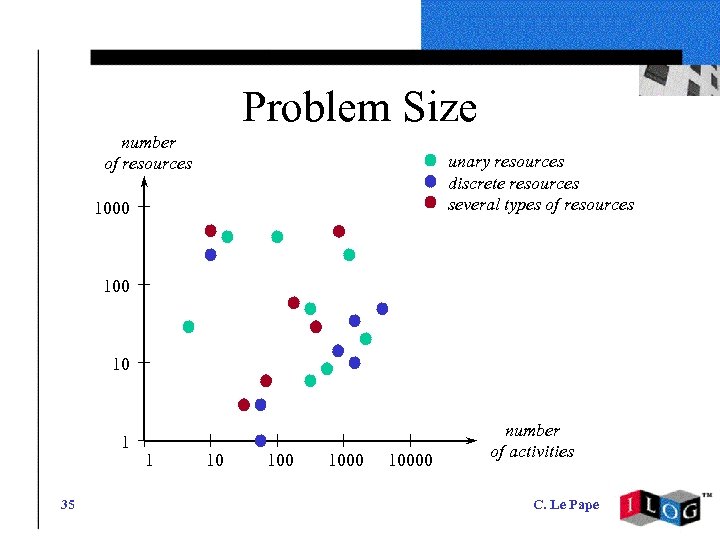Problem Size number of resources unary resources discrete resources several types of resources 1000 10 1 35 1 10 10000 number of activities C. Le Pape

Suitable Response Time • Reactive train traffic control: two seconds • Predictive production and maintenance scheduling: minutes to hours • Reactive production and maintenance scheduling: seconds • Predictive timetabling: minutes to hours • Reactive computer or printer job scheduling: small fraction of the average job duration 36 C. Le Pape

Outline • Constraint Programming • Constraint-Based Scheduling – Scheduling Problems – Propagation of Temporal Constraints – Propagation of Resource Constraints – Examples of Applications • Cooperative Problem-Solving 37 C. Le Pape

Variables (Definition) From now on, we focus on interval activities … Three variables start(A) end(A) duration(A) for each activity A 38 C. Le Pape

Variables (Implementation) • Finite domain (bit vector) – The domain of each variable is a finite set • Interval domain (pair of numbers) – The domain of each variable is an interval startmin(A), startmax(A), endmin(A), endmax(A) durationmin(A), durationmax(A) 39 C. Le Pape

Basic Relation end(A) = start(A) + duration(A) endmin(A) = max(endmin(A), startmin(A) + durationmin(A)) endmax(A) = min(endmax(A), startmax(A) + durationmax(A)) startmin(A) = max(startmin(A), endmin(A) - durationmax(A)) startmax(A) = min(startmax(A), endmax(A) - durationmin(A)) durationmin(A) = max(durationmin(A), endmin(A) - startmax(A)) durationmax(A) = min(durationmax(A), endmax(A) - startmin(A)) 40 C. Le Pape

Temporal Constraints • Simple precedence constraints start(A) £ start(B) start(A) £ end(B) end(A) £ start(B) end(A) £ end(B) 41 C. Le Pape

Temporal Constraints • Precedence constraints with minimal delays start(A) + delay £ start(B) start(A) + delay £ end(B) end(A) + delay £ start(B) end(A) + delay £ end(B) 42 C. Le Pape

Temporal Constraints • Precedence constraints with fixed delays start(A) + delay = start(B) start(A) + delay = end(B) end(A) + delay = start(B) end(A) + delay = end(B) 43 C. Le Pape

Temporal Constraints • Maximal delays start(A) £ start(B) + delay start(A) £ end(B) + delay end(A) £ start(B) + delay end(A) £ end(B) + delay 44 C. Le Pape

Propagation of Time Bounds var(A) + delay £ var(B) varmin(B) = max(varmin(B), varmin(A) + delay) varmax(A) = min(varmax(A), varmax(B) - delay) Complete propagation for bounded domains – Contradiction found when the constraints conflict – Best possible varmin(A) and varmax(A) found otherwise – Incremental variant of an operations research algorithm for project scheduling (PERT networks) 45 C. Le Pape

Propagation of Time Bounds Complexity – For a consistent network: O(n*m) where n is the number of activities and m the number of constraints if constraints are propagated in the first-in first-out order – For an inconsistent network: O(h*n 2) where h is the time horizon (can be reduced to O(n*m) but not always worth it in practice) 46 C. Le Pape

Minimal and Maximal Distances • [x + dxy £ y] and [y + dyz £ z] implies [x + (dxy + dyz) £ z] • Useful to solve disjunctions of temporal constraints [x - 5 £ y] [y + 2 £ z] [z + 4 £ x] OR [v + 3 £ w] 47 C. Le Pape

Minimal and Maximal Distances Matrix-based method Whenever dxy is modified, update dwz to max(dwz, dwx + dxy + dyz) Complexity – O(n 2) after each modification of the constraint network – O(n 3) to initialize the matrix 48 C. Le Pape

Outline • Constraint Programming • Constraint-Based Scheduling – Scheduling Problems – Propagation of Temporal Constraints – Propagation of Resource Constraints – Examples of Applications • Cooperative Problem-Solving 49 C. Le Pape

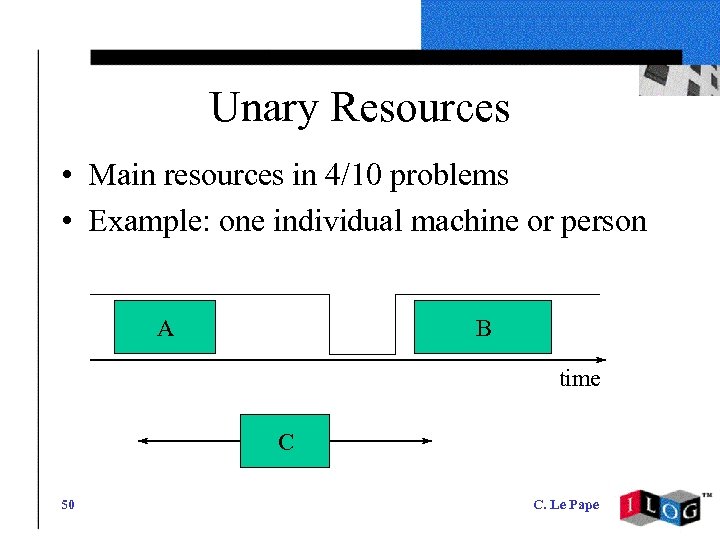Unary Resources • Main resources in 4/10 problems • Example: one individual machine or person A B time C 50 C. Le Pape

Discrete Resources • Main resources in 5/10 problems • Example: group of identical machines B A C time D 51 C. Le Pape

State Resources • Main resources in 1/20 problems • Example: oven with different temperatures B A C time D 52 C. Le Pape

Energetic Resources • Main resources in 1/20 problems • Example: number of man-days per week A B time C 53 C. Le Pape

Constraint Propagation Models • • 54 Explicit time-tables Disjunctive constraints Energetic reasoning Edge finding (task intervals) C. Le Pape

Explicit Time-Tables (UD) • WA(t) = [start(A) £ t < end(A)] • "t, SA [WA(t) * capacity(A)] £ capacity(t) A C B time C 55 C. Le Pape

Explicit Time-Tables (S) • WA(t) = [start(A) £ t < end(A)] • "t, WA(t) implies [state(A) = state(t)] B D A C time D 56 C. Le Pape

Explicit Time-Tables (E) • • • a. A(I) = max(0, endmin(A) - start(I)) b. A(I) = max(0, end(I) - startmax(A)) d(I) = end(I) - start(I) d(A) = durationmin(A) WA(I) = min(a. A(I), b. A(I), d(A)) • SA [WA(I) * capacity(A)] £ capacity(I) 57 C. Le Pape

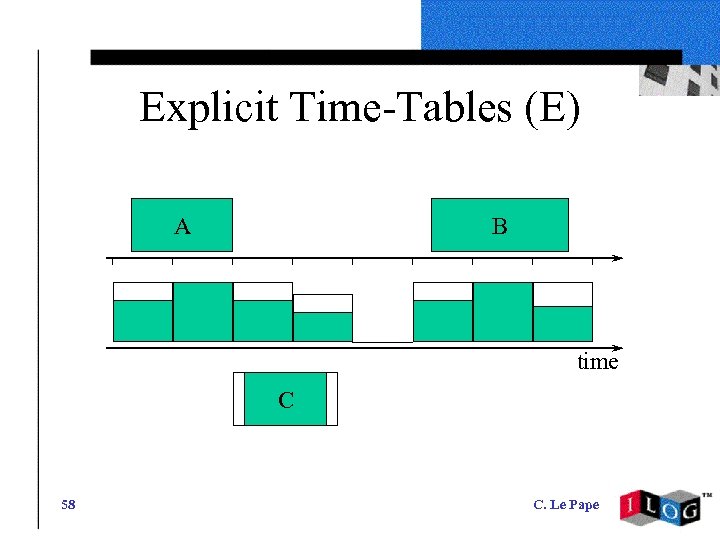Explicit Time-Tables (E) A B time C 58 C. Le Pape

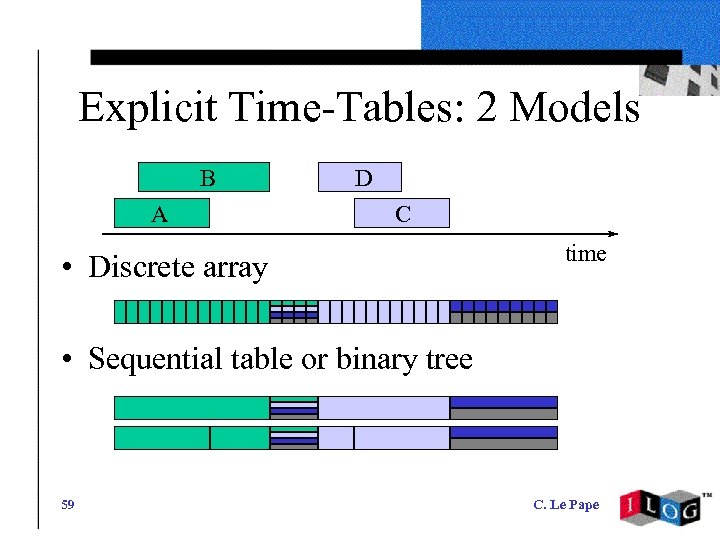Explicit Time-Tables: 2 Models B A D C • Discrete array time • Sequential table or binary tree 59 C. Le Pape

Explicit Time-Tables: Extensions • Minimal capacity constraints (UDE) • Default state (S) • Constraints between time-tables or between time-tables and other variables (UDES) 60 C. Le Pape

Disjunctive Constraints (U) • [end(A) £ start(B)] OR [end(B) £ start(A)] • • 61 [endmin(A) > startmax(B)] implies [end(B) £ start(A)] [endmin(B) > startmax(A)] implies [end(A) £ start(B)] C. Le Pape

Disjunctive Constraints (U) • Optional activities – Resource alternatives – Sub-contracts • Transition times – Tool setups – Color changes – Cleaning 62 C. Le Pape

Disjunctive Constraints (U) • 63 [end(A) + ttime(A, B) £ start(B)] OR [end(B) + ttime(B, A) £ start(A)] OR [duration(A) = 0] OR [duration(B) = 0] OR [capacity(A) = 0] OR [capacity(B) = 0] C. Le Pape

Energetic Reasoning (UD) • • • a. A(I) = max(0, endmin(A) - start(I)) b. A(I) = max(0, end(I) - startmax(A)) d(I) = end(I) - start(I) d(A) = durationmin(A) WA(I) = min(a. A(I), b. A(I), d(A)) • SA [WA(I) * capacity(A)] £ capacity(I) 64 C. Le Pape

Energetic Reasoning (UD) • Habographs [Beck 92] – Intervals: [id. . jd) or [b + id. . b + jd) • Energetic resources [Le Pape 94] – Intervals: [id. . (i+1)d) or [b + id. . b + (i+1)d) • Energetic reasoning rules [Lopez 91] – Intervals: [startmin(A). . endmax(B)) or [startmin(A). . x) 65 C. Le Pape

Energetic Reasoning (U) • I = [startmin(A). . endmax(B)) • d(I) < SC<>A, BWC(I) + d(A) + d(B) implies [end(B) £ start(A)] A[1. . 8 - 2 - 3. . 10] B[0. . 3 - 2. . 5] C[2. . 4 - 1 - 3. . 5] I = [1. . 5) [4 < 1 + 2] implies [2 £ start(A)] 66 C. Le Pape

Edge Finding (U) • Basic idea Prove that an activity A executes before (or after) a set of other activities W • Notations smin(W) = min. BÎW startmin(B) emax(W) = max. BÎW endmax(B) dmin(W) = SBÎW durationmin(B) 67 C. Le Pape

Edge Finding (U) • emax(W) < smin(W + {A}) + dmin(W + {A}) implies [smin(W') + dmin(W') £ start(A)] for every W' included in W A[0. . 11 - 6. . 17] B[1. . 7 - 4 - 5. . 11] C[1. . 8 - 3 - 4. . 11] W = {B C} [11 < 0 + 13] implies [1 + 7 £ start(A)] 68 C. Le Pape

Edge Finding (U) • Jackson's Preemptive Schedule [Pinson 88] [Carlier & Pinson 90/94] – O(n 2) O(n*log(n)) • Iterative algorithm [Nuijten 94] – O(n 2) with no specific data structure • Task intervals [Caseau & Laburthe 94] – O(n 3) – Incremental – More deductions è more precise time-bounds 69 C. Le Pape

Edge Finding (U) • "Not-first" deduction rule emax(W) < smin(A) + dmin(W + {A}) implies [min. BÎW(smin(B) + dmin(B)) £ start(A)] • [Nuijten 94] [Caseau & Laburthe 94] • [Baptiste & Le Pape 96]: Complete application in O(n 2) time and O(n) space 70 C. Le Pape

Edge Finding (U) • "Not-first" deduction rule with knapsack D = smin(A) + dmin(W + {A}) - emax(W) > 0 implies [min. W' | f(W')(smin(W') + dmin(W')) £ start(A)] with f(W') defined as [W = W' OR D £ dmin(W')] • Complete application in exponential time (includes the NP-complete knapsack problem) • Partial application [Caseau & Laburthe 95] 71 C. Le Pape

Comparison • Theoretical results – Unique fix point semantics – Modeling power – Time and space complexity – Pruning power • Experimental results 72 C. Le Pape

Outline • Constraint Programming • Constraint-Based Scheduling – Scheduling Problems – Propagation of Temporal Constraints – Propagation of Resource Constraints – Examples of Applications • Cooperative Problem-Solving 73 C. Le Pape

MSS: Problem Definition (1) Molding Shop Scheduling • 2 types of cast-iron (standard and special) • For each cast-iron type: – available quantity every hour • 3 molding machines • For each machine: – shifts – breaks (lunch, maintenance) – periods during which the machine can manufacture only some types of parts 74 C. Le Pape

MSS: Problem Definition (2) • 30 types of parts • For each part type: – cast-iron type – one or more possible machines • For each (part, machine) pair: – – – 75 production speed cast-iron consumption minimal and maximal batch size maximal break duration (one break per batch allowed) minimal production time before and after the break C. Le Pape

MSS: Problem Definition (3) • 200 orders for parts • For each order: – part type – number of parts – due-date • Optimization criterion – relaxation of due-dates – closer due-dates are more important than further due-dates 76 C. Le Pape

MSS: Problem Representation (1) • Part type = Discrete resource – Produced by activities – Due-dates è minimal production constraints • Machine = State resource – Part type produced at time t = state at time t – Default state 0 out of shifts and during breaks • Cast-iron type = Energetic resource 77 C. Le Pape

MSS: Problem Representation (2) • Minimal and maximal number of (ordered) batches for each (part, machine) pair • Batch = 3 Interval activities – – – – 78 BB before the break, B for the break, AB after the break end(BB) = start(B) and end(B) = start(AB) duration(BB) not in [1, minimal-duration-before-break - 1] duration(AB) not in [1, minimal-duration-after-break - 1] duration(B) £ maximal-break-duration batch-duration = duration(BB) + duration(AB) batch-duration £ maximal-batch-size / production-rate batch-duration not in [1, (minimal-batch-size - 1) / production-rate] C. Le Pape

MSS: Problem Representation (3) • Resource constraints – – BB and AB require the machine in the "part type" state BB and AB require the cast-iron at the given consumption rate B requires the machine in the state 0 AB produces the batch of parts (batch-duration * production-rate units of the part type) • Redundant constraints – From start(BB) to end(AB), the state of the machine is either 0 or "part-type" – Counter of the minimal and maximal production of each part type each day 79 C. Le Pape

MSS: Search Procedure • Select a batch with unbound start time or unbound duration – If the batch is optional: • either confirm or cancel the batch – Else if the start time is unbound: • either schedule (ASAP) or postpone the batch – Else (the duration is unbound): • instantiate the duration • Iterate 80 C. Le Pape

MSS: Results • 2200 lines of ILOG SCHEDULER source code – 1400 lines for representing the problem – 600 lines for reading the data – 200 lines for solving the problem • Executable – 880 K on an IBM RS 600 – 420 K on a SUN-4 • CPU time (for 300 non-zero activities and 40 resources) – In most cases: 10 seconds – When more: search is stopped and restarted with relaxed due-dates 81 C. Le Pape

CSS: Problem Definition Construction Site Scheduling Resource-constrained project scheduling problem with: – – – – – 82 1 unary resource and 3 discrete resources 15 interval activities and 15 interruptible activities 15 activities with time-versus-capacity tradeoffs 10 activities with variable requirements over time temporal constraints periods during which a resource is not or not fully available percentage constraints synchronization constraints 40 preference constraints (10 levels of preferences) C. Le Pape

CSS: Search Procedure • Select preferences • Impose the selected preferences as constraints • Search for a solution within a limited number of backtracks (blend of preemptive job-shop scheduling and resource-constrained project scheduling) • Save the solution if one is found • Iterate with a different set of preferences 83 C. Le Pape

CSS: Results • 2200 lines of CLAIRE source code (+ 2200 lines library) – 1100 lines for representing the problem – 300 lines for reading the data – 800 lines for solving the problem • 3000 lines for the graphical interface • Executable – 1130 K on a PC under OS 2 (with graphical interface) • CPU time (for 30 activities and 4 resources) – "Good" schedules obtained in 5 to 10 iterations – 15 seconds per iteration 84 C. Le Pape

Outline • Constraint Programming • Constraint-Based Scheduling • Cooperative Problem-Solving 85 C. Le Pape

Outline • Constraint Programming • Constraint-Based Scheduling • Cooperative Problem-Solving – Introduction – Problem Decomposition – Constraint Propagation – Search 86 C. Le Pape

Problem Solving • Two main other classes of techniques – Linear Programming and Mixed Integer Programming – Local Search 87 C. Le Pape

Mixed Integer Programming (1) • Explicit problem definition – Linear constraints – Real (floating point) and integer variables – One optimization criterion • Separation between problem definition and problem solving • The continuous relaxation (when fractional values are allowed for integer variables) is solvable in polynomial time Ø Bound on optimization criterion Ø Guidance for solving the MIP problem by branch-and-bound (rounding, cuts, …) 88 C. Le Pape

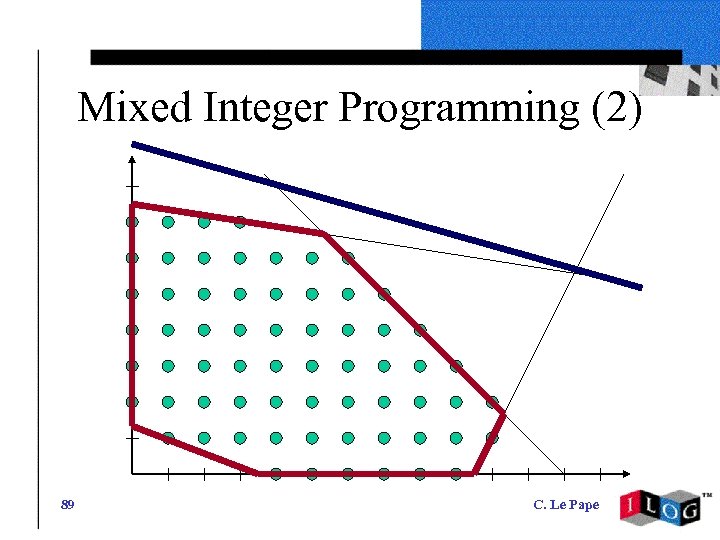Mixed Integer Programming (2) 89 C. Le Pape

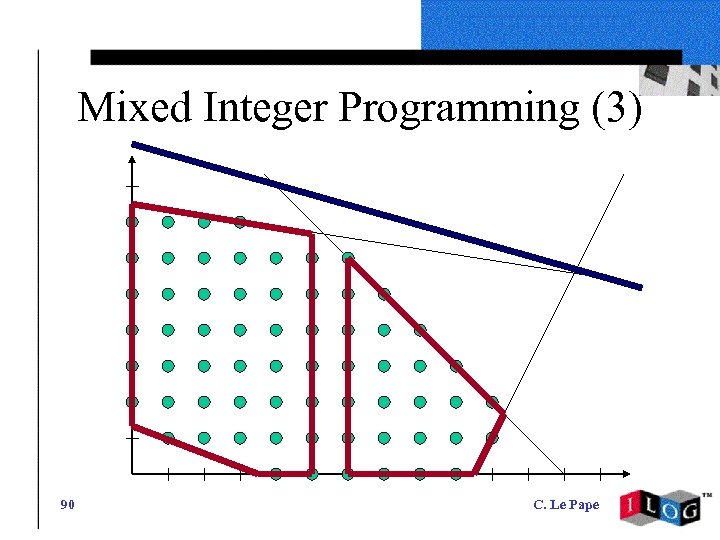Mixed Integer Programming (3) 90 C. Le Pape

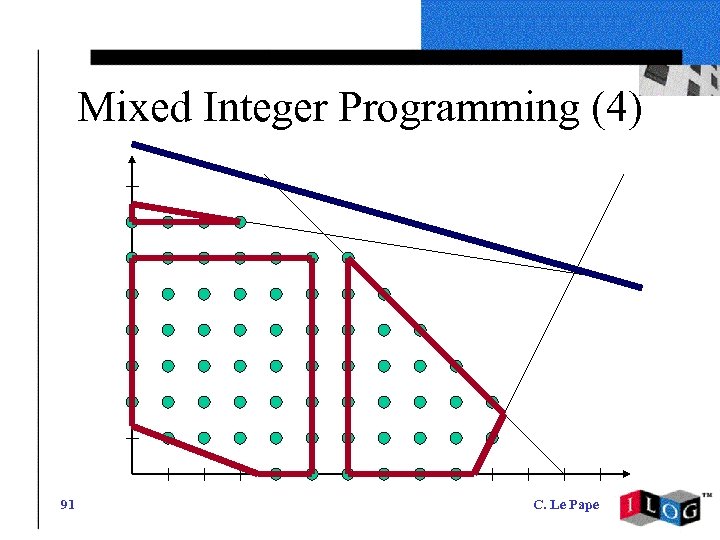Mixed Integer Programming (4) 91 C. Le Pape

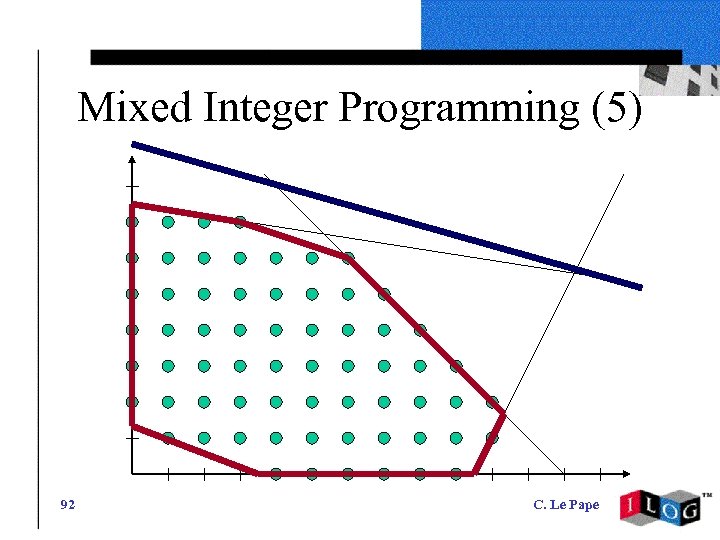Mixed Integer Programming (5) 92 C. Le Pape

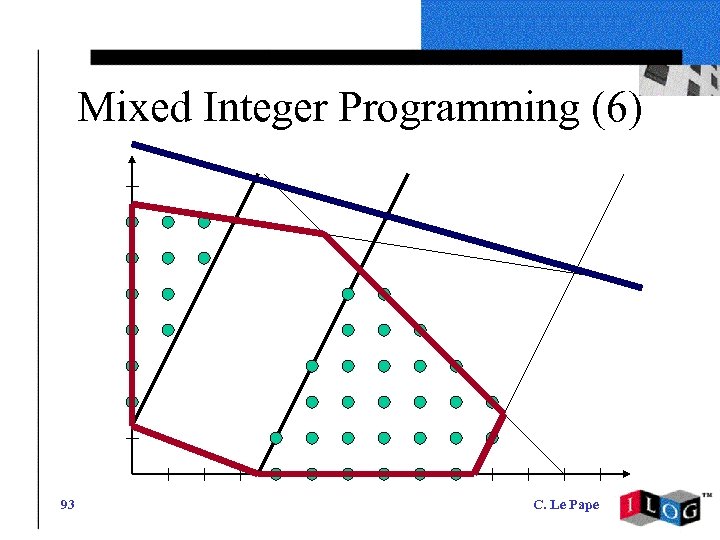Mixed Integer Programming (6) 93 C. Le Pape

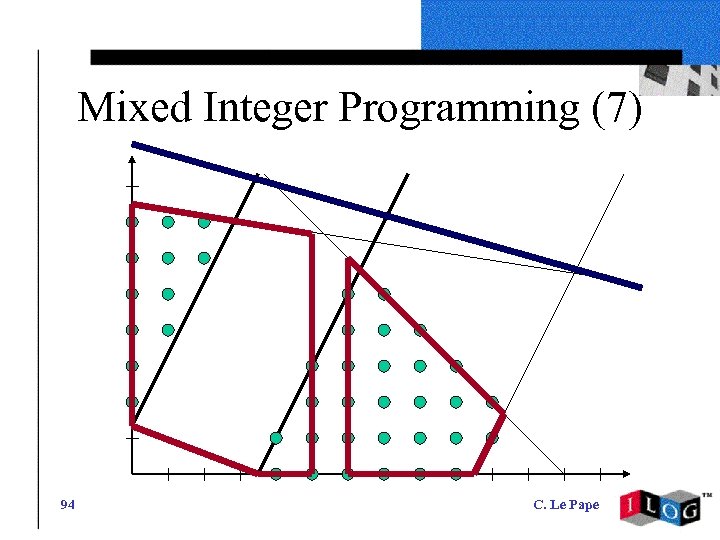Mixed Integer Programming (7) 94 C. Le Pape

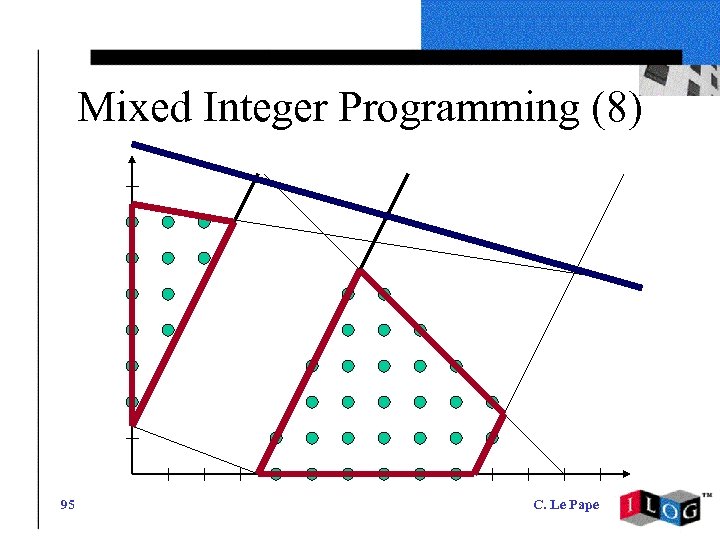Mixed Integer Programming (8) 95 C. Le Pape

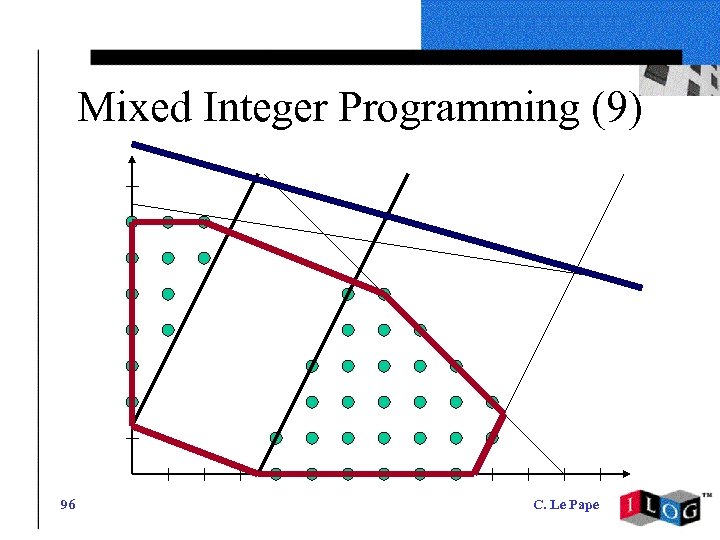Mixed Integer Programming (9) 96 C. Le Pape

MIP/CP: Most Important Points MIP CP • Linear constraints • One relaxation of the global problem • Guidance from the optimal solution of the relaxed problem • Cuts • Any constraints • Linked relaxations of multiple sub-problems • Guidance from the possible solutions of the relaxed sub-problems • Redundant constraints • Scheduling example: hard to deal with resource constraints • Scheduling example: hard to deal with « sum » cost functions 97 C. Le Pape

MIP/CP: Most Important Points Resource sub-problem Temporal sub-problem Resource sub-problem Cost function sub-problem 98 C. Le Pape

Local Search • Operators to move from solutions to other (neighbor) solutions (or from populations of solutions to populations of solutions) • Search control strategy (meta-heuristic) • Many different types: simulated annealing, tabu search, genetic algorithms, … 99 C. Le Pape

Main Issues (1) • Mixed Integer Programming – Is the continuous relaxation a good approximation of the convex envelope of the solutions? – Can the formulation of the problem be iteratively modified to make the optimal solution of the continuous relaxation converge toward the optimal solution of the initial problem? 100 C. Le Pape

Main Issues (2) • Constraint Programming – Are the critical constraints propagating well? – Is a tight bound on the optimization criterion efficiently translated (by propagation) into constraints that effectively guide the search toward a solution? 101 C. Le Pape

Main Issues (3) • Local Search – Is the neighborhood topology consistent with the optimization criterion? – Are the operators connecting (in a few steps) good solutions with better solutions, without downgrading the solution too much in intermediate steps? 102 C. Le Pape

Outline • Constraint Programming • Constraint-Based Scheduling • Cooperative Problem-Solving – Introduction – Problem Decomposition – Constraint Propagation – Search 103 C. Le Pape

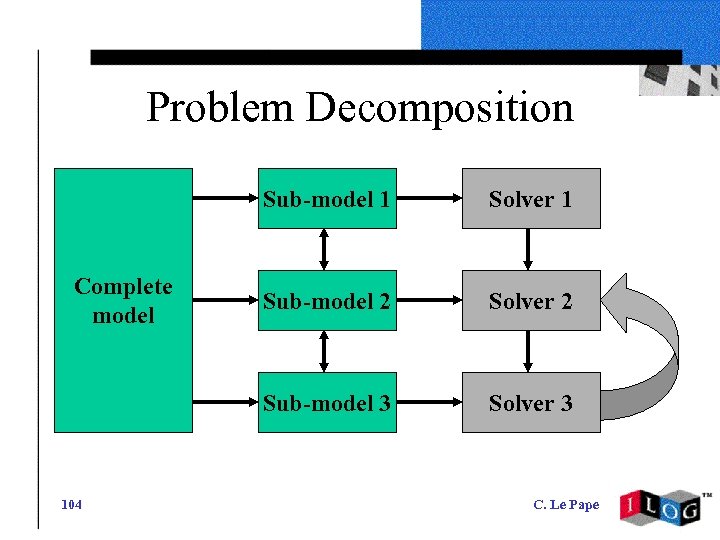Problem Decomposition Sub-model 1 104 Sub-model 2 Solver 2 Sub-model 3 Complete model Solver 1 Solver 3 C. Le Pape

Sequential Decomposition • Solve sub-problem 1 • Impose the solution of sub-problem 1 and solve sub-problem 2 • Infer characteristics of « good » solutions of sub-problem 1 • Iterate 105 C. Le Pape

Column Generation • Generate candidate solution components • Find the optimal combination of these components • Infer characteristics of « good » solution components to add • Iterate 106 C. Le Pape

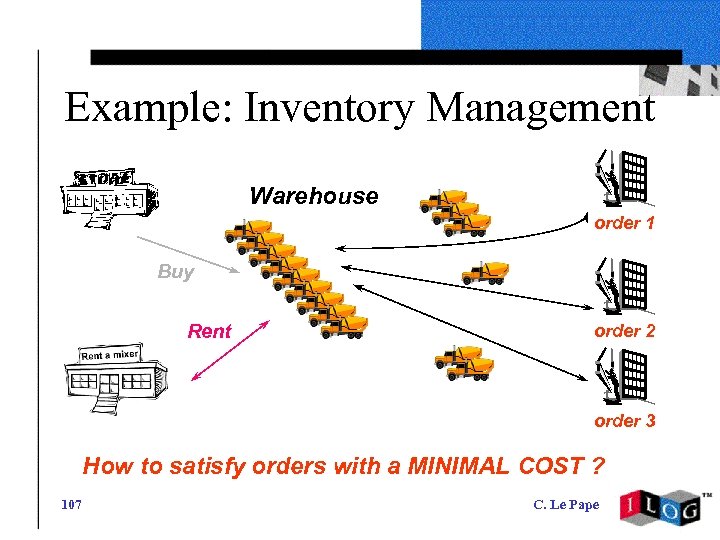Example: Inventory Management Warehouse order 1 Buy Rent order 2 order 3 How to satisfy orders with a MINIMAL COST ? 107 C. Le Pape

Example Stock = 4 st(o 1) = 0, et(o 1) = 35, rq(o 1) = 2 st(o 2) = 5, et(o 2) = 30, rq(o 2) = 3 st(o 3) = 32, et(o 3) = 87, rq(o 3) = 5 rq(o 1)=2 rq(o 2)=3 0 108 5 rq(o 3)=5 32 87 100 C. Le Pape

Maintenance Constraints • No resource is used more than Utime units without maintenance • No more than Mnumber resources are in maintenance at the same time • Cost of each maintenance: Cmaint 109 C. Le Pape

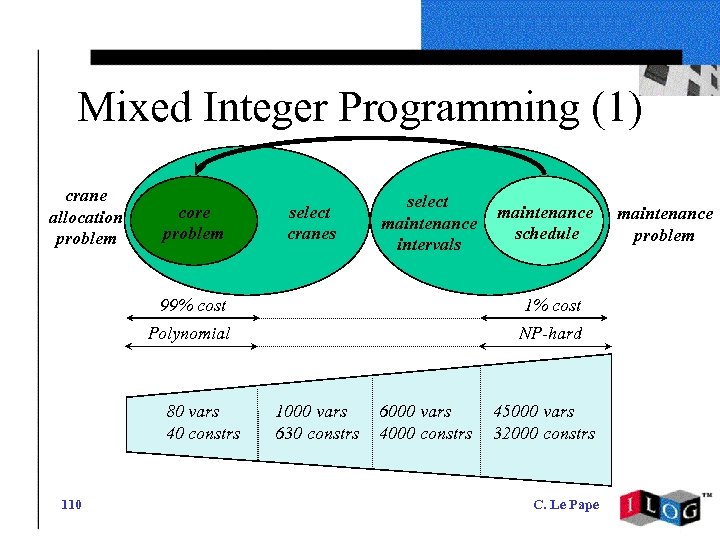Mixed Integer Programming (1) crane allocation problem core problem select cranes select maintenance intervals maintenance schedule 99% cost 1% cost Polynomial NP-hard 80 vars 40 constrs 110 1000 vars 630 constrs 6000 vars 4000 constrs 45000 vars 32000 constrs C. Le Pape maintenance problem

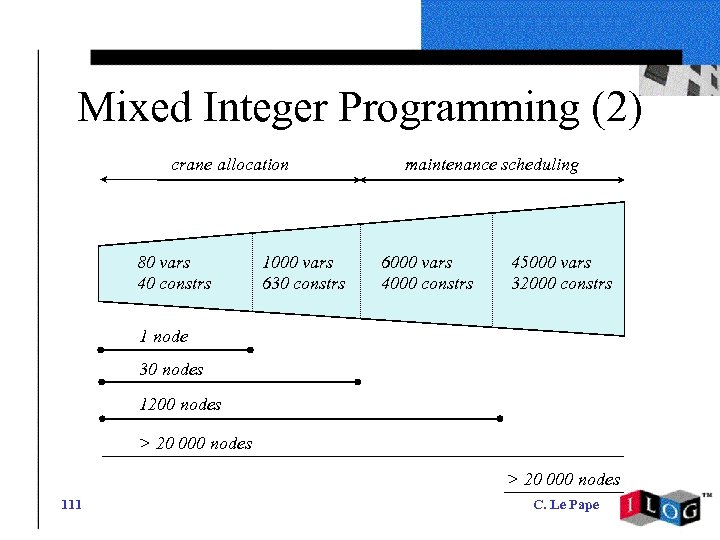Mixed Integer Programming (2) crane allocation 80 vars 40 constrs 1000 vars 630 constrs maintenance scheduling 6000 vars 4000 constrs 45000 vars 32000 constrs 1 node 30 nodes 1200 nodes > 20 000 nodes 111 C. Le Pape

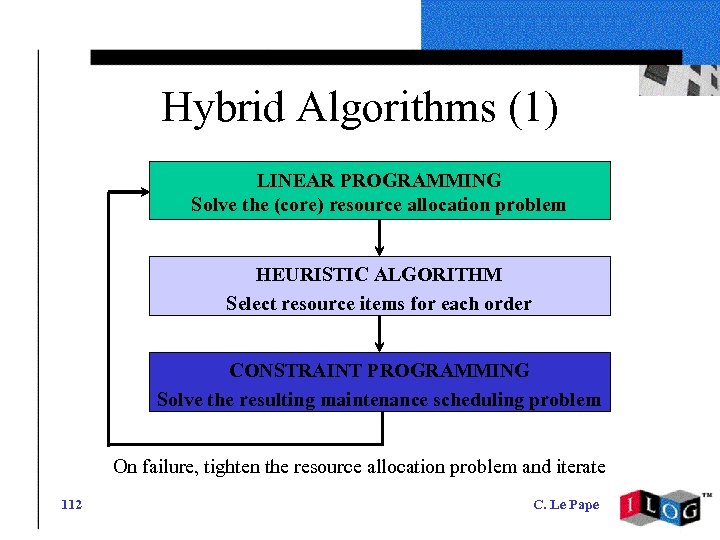Hybrid Algorithms (1) LINEAR PROGRAMMING Solve the (core) resource allocation problem HEURISTIC ALGORITHM Select resource items for each order CONSTRAINT PROGRAMMING Solve the resulting maintenance scheduling problem On failure, tighten the resource allocation problem and iterate 112 C. Le Pape

Hybrid Algorithms (2) Tightness of the crane allocation problem: • Extend the duration of all tasks (add the maintenance duration) • Extend the duration of the conflict task Tightness: Resource allocation cost: Maint. scheduling cost: dur(o) + 1*dur(m) dur(o) + 2*dur(m) dur(o) + 3*dur(m) dur(o) + 4*dur(m) 87 927 919 88 022 342 89 123 491 90 211 387 91 910 152 2501 Final result: 4. 5% above the lower bound 87 927 919 113 C. Le Pape

Hybrid Algorithms (3) • Other hybrid algorithms, including column generation, provided « good » solutions • Some instances remain « hard » • Details available in [Caseau & Kökény 98, Baptiste et al. 98] 114 C. Le Pape

Outline • Constraint Programming • Constraint-Based Scheduling • Cooperative Problem-Solving – Introduction – Problem Decomposition – Constraint Propagation – Search 115 C. Le Pape

LP as a Global Constraint • Collection of linear constraints (general or of a particular form) treated as a global constraint – Detect conflicts – Find variables with fixed values – Find bounds of variables – Infer additional constraints (cuts) 116 C. Le Pape

Objective Functions • Minimize COST = F(V 1, V 2, …, Vn) • Apply linear programming (or an operations research algorithm) to a relaxation of the problem – Global lower bound at the root of the search tree – Lower bound LB at each node of the search tree – Characteristics of solutions with COST < LB + D inferred from the optimal solution of the relaxed problem and « reduced costs » 117 C. Le Pape

Outline • Constraint Programming • Constraint-Based Scheduling • Cooperative Problem-Solving – Introduction – Problem Decomposition – Constraint Propagation – Search 118 C. Le Pape

Example: Vehicle Routing • Efficient local search algorithms – No specific constraint – Incremental computation of tour length and cost from a solution to its neighbors • Constraint programming for specific constraints – Use constraints to test and reject « bad » neighbors – Enlarge the neighborhood if there is no valid neighbor – Find the valid neighbor with the smallest cost • References – [Pesant & Gendreau 96, Shaw 98, Kilby, Prosser & Shaw 00] – [Caseau & Laburthe 99, Caseau et al. 01] 119 C. Le Pape

Examples: Scheduling • Forget and extend – Random fragments [Baptiste, Le Pape & Nuijten 95, Nuijten & Le Pape 98] – Chosen fragments [Caseau et al. 01] • Minimal perturbation – [El Sakkout & Wallace 00] 120 C. Le Pape

Conclusion (1) • Already a significant number of applications • Credo: hybrid problem-solving techniques will enable the resolution of problems that are still open today – More efficient exact resolution – Better lower and upper bounds in given CPU time – More robust algorithms 121 C. Le Pape

Conclusion (2) • Main difficulties – Identification of promising combinations of techniques – Implementation and test of several of these combinations • Guidelines and tools are needed – Modeling – Combination of sub-models – Testing and interpretation of test results 122 C. Le Pape

References (1) Disclaimer: not (at all) a complete bibliography! • • • 123 K. R. Baker. Introduction to Sequencing and Scheduling. John Wiley and Sons, 1974. Ph. Baptiste, C. Le Pape and W. Nuijten. Constraint-Based Optimization and Approximation for Job Shop Scheduling. IJCAI'95 Workshop on Intelligent Manufacturing Systems, 1995. Ph. Baptiste and C. Le Pape. Edge-Finding Constraint Propagation Algorithms for Disjunctive and Cumulative Scheduling. 15 th Workshop of the U. K. Planning Special Interest Group, 1996. Ph. Baptiste, Y. Caseau, T. Kökény, C. Le Pape and R. Rodosek. Creating and Evaluating Hybrid Algorithms for Inventory Management Problems. 4 th National Meeting on Practical Approaches to NP‑Complete Problems, 1998. H. Beck. Constraint Monitoring in TOSCA. AAAI Spring Symposium on Practical Approaches to Planning and Scheduling, 1992. C. Le Pape

References (2) • • • 124 J. Carlier and E. Pinson. A Practical Use of Jackson's Preemptive Schedule for Solving the Job-Shop Problem. Annals of Operations Research, 26: 269 -287, 1990. J. Carlier and E. Pinson. Adjustment of Heads and Tails for the Job-Shop Problem. European Journal of Operational Research, 78(2): 146 -161, 1994. Y Caseau and F. Laburthe. Improved CLP Scheduling with Task Intervals. 11 th International Conference on Logic Programming, 1994. Y. Caseau and F. Laburthe. Disjunctive Scheduling with Task Intervals. Technical Report, Ecole Normale Supérieure, 1995. Y. Caseau and T. Kökény. An Inventory Management Problem. Constraints, 3(4): 363 -373, 1998. Y. Caseau and F. Laburthe. Heuristics for Large Constrained Vehicle Routing Problems. Journal of Heuristics, 5: 281 -303, 1999. C. Le Pape

References (3) • • • 125 Y. Caseau, F. Laburthe, C. Le Pape and B. Rottembourg. Combining Local and Global Search in a Constraint Programming Environment. Knowledge Engineering Review, to appear. H. El Sakkout and M. Wallace. Probe Backtrack Search for Minimal Perturbation in Dynamic Scheduling. Constraints, 5(4): 359 -388, 2000. P. Kilby, P. Prosser and P. Shaw. A Comparison of Traditional and Constraint-based Heuristic Methods on Vehicle Routing Problems with Side Constraints, 5(4): 389 -414, 2000. C. Le Pape. Implementation of Resource Constraints in ILOG SCHEDULE: A Library for the Development of Constraint‑Based Scheduling Systems. Intelligent Systems Engineering, 3(2): 55 -66, 1994. P. Lopez. Approche énergétique pour l'ordonnancement de tâches sous contraintes de temps et de ressources. Thèse de l'Université Paul Sabatier, 1991. C. Le Pape

References (4) • • • 126 W. Nuijten. Time and Resource Constrained Scheduling: A Constraint Satisfaction Approach. Ph. D Thesis, Eindhoven University of Technology, 1994. W. Nuijten and C. Le Pape. Constraint-Based Job Shop Scheduling with ILOG Scheduler. Journal of Heuristics, 3: 271 -286, 1998. G. Pesant and M. Gendreau. A View of Local Search in Constraint Programming. 2 nd International Conference on Principles and Practice of Constraint Programming, 1996. E. Pinson. Le problème de job-shop. Thèse de l'Université Paris VI, 1988. P. Shaw. Using Constraint Programming and Local Search Methods to Solve Vehicle Routing Problems. 4 th International Conference on Principles and Practice of Constraint Programming, 1998. C. Le Pape