Conjunctive Grammars and Alternating Automata Tamar Aizikowitz and

Conjunctive Grammars and Alternating Automata Tamar Aizikowitz and Michael Kaminski Technion – Israel Institute of Technology Wo. LLIC 2008 Heriot-Watt University

Introduction: ND Computational Models l Non-deterministic computational models have existential acceptance conditions l l l At least one computation must accept E. g. , FSA, PDA, CFG, TM Languages accepted have disjunctive quality l l A word must meet one of many possible conditions (computations) Language class closed under union 2 of 25

Introduction: Co-ND Computational Models l Dual computational models have universal acceptance conditions l l l All computations must accept E. g. , Universal TM; accepts class Co-NP Languages accepted have conjunctive quality l l A word must meet all conditions (computations) Language class closed under intersection 3 of 25

Introduction: Combined Computational Models l Several models combining existential and universal computations have been explored. l We explore extensions of models for Context Free Languages. l Specifically: l l Conjunctive Grammars Alternating Pushdown Automata 4 of 25

Introduction: Conjunctive Grammars (CG) l Introduced by Alexander Okhotin in 2001* l Extension of Context Free Grammars l Add power of explicit intersection Reminder: Context free languages are not closed under intersection… l CG-s generate a larger class of languages * Okhotin A. , Conjunctive Grammars, Journal of Automata, Languages and Combinatorics 6(4) (2001) 519 -535 5 of 25

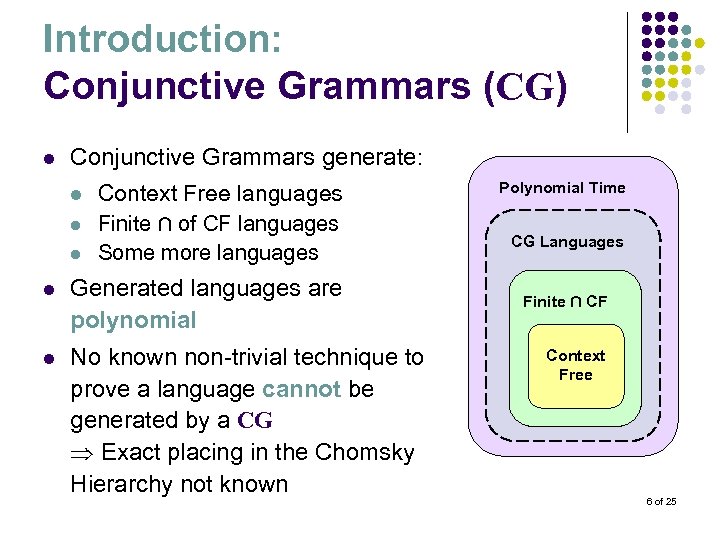Introduction: Conjunctive Grammars (CG) l Conjunctive Grammars generate: l l l Context Free languages Finite ∩ of CF languages Some more languages l Generated languages are polynomial l No known non-trivial technique to prove a language cannot be generated by a CG Exact placing in the Chomsky Hierarchy not known Polynomial Time CG Languages Finite ∩ CF Context Free 6 of 25

Introduction: Alternating Automata l Alternating Automata were introduced by Chandra et. al. in 1981* l Computations alternate between existential and universal acceptance modes l Well known examples: l l l Alternating Finite State Automata (Verification) Alternating Turing Machines (Complexity Theory) Both equivalent to non-alternating counterparts * Chandra, A. K. , Kozen, D. C. , Stockmeyer, L. J. , Alternation. Journal of the ACM 28(1) (1981) 114 -133 7 of 25

Introduction: Alternating Pushdown Automata (APDA) l Further explored by Ladner et. al. in 1984* l Add conjunction to computations l Not equivalent to standard PDA model l Accept exactly the Exp. Time Languages l Not equivalent to the CG model * Ladner, R. E. , Lipton, R. J. , Stockmeyer, L. J. , Alternating pushdown and stack automata. SIAM Journal on Computing 13(1) (1984) 135 -155 8 of 25

Introduction: Synchronized APDA (SAPDA) l We introduce a new model: Synchronized Alternating Pushdown Automata l Equivalent to Conjunctive Grammar model l In fact, this is the first class of automata suggested for Conjunctive Grammars 9 of 25

Outline l Conjunctive Grammars l Synchronized Alternating PDA l Equivalence Results: CG ~ SAPDA l Future Work 10 of 25

Conjunctive Grammars: Model Definition l l l G = (V, T, P, S) V, T, S as in the standard CFG case P contains rules X → ( 1 & & n) l l n = 1 gives standard CFG rules Conjunctive Formulas: l l l { } V T are formulas If and are formulas then is a formula If 1, …, n are formulas then ( 1 & & n) is a formula conjunct 11 of 25

Conjunctive Grammars: Model Definition l Derivation: l l s 1 X s 2 s 1( 1 & & n)s 2 s. t. X → ( 1 & & n) P l l Application: Contraction: s 1(w & & w) s 2 s 1 w s 2 Language: L(G) = {w T * | S * w} Note: ( & ) *w iff *w and *w 12 of 25

Conjunctive Grammars: Example 1 l L = {anbncn | n } l Note: L = L 1 L 2 where l l l L 1 = {anbnci | n, i } L 2 = {aibncn | n, i } G = ({S, S 1, S 2, S 3, S 4} , {a, b, c} , S , P) where P = : l l l S 1 → a S 1 b | ; S 2 → c S 2 | S 3 → a S 3 | ; S 4 → b S 4 c | S → (S 1 S 2 & S 3 S 4) L 1 L 2 S 1 S 2 * L 1 S 3 S 4 * L 2 13 of 25

Conjunctive Grammars: Example 1 l Derivation of aaabbbccc: → a. S S (S 1 S 2 & S 3 S 4) (a. S 1 b. S 2 & S 3 S 4) S → (S Sb & S S ) … (aaa. S 1 bbb. S 2 & S 3 S 4) S → a. S b (aaabbb. S 2 & S 3 S 4) S → c. S (aaabbbc. S 2 & S 3 S 4) … (aaabbbccc & S 3 S 4) S → c. S contraction … (aaabbbccc & aaabbbccc) aaabbbccc 1 112 1 3 4 1 1 2 2 14 of 25

Conjunctive Grammars: Interesting Languages l CGs can generate some interesting languages: l l Multiple agreement: {anbncn | n } Cross agreement: {anbmcndm | n, m } Reduplication: {w$w | w {a, b}*} all mildly context-sensitive languages (MCS) l CGs can also generate “stronger” languages such as: {ba 2 ba 4 ba 2 nb | n } l not MCS because not semi-linear! 15 of 25

Synchronized Alternating Pushdown Automata (SAPDA) l l Extension of the standard PDA model Transitions are to conjunctions of (state, stack -word) pairs l E. g. (q , , X ) = {( p 1 , XX ) ( p 2 , Y ) , ( p 3 , Z ) } Non-deterministic model = many possible conjunctions l If all conjunctions are of one pair then we have the standard PDA model 16 of 25

Synchronized Alternating Pushdown Automata (SAPDA) l l Stack memory is a tree Each leaf has a separate processing head q D C A p B A l l l A conjunctive transition to n pairs splits the current branch to n branches Branches are processed independently Sibling branches must empty synchronously. 17 of 25

SAPDA: Model Definition l l A = (Q , , q 0 , ) For every (q , , X ) Q ( { }) (q , , X ) {(q 1 , 1) (qn , n) | qi Q , i * , n } l Example: (q , , X ) = {( p 1 , Z ) ( p 2 , YY )} q X p 1 Z Y Y p 2 18 of 25

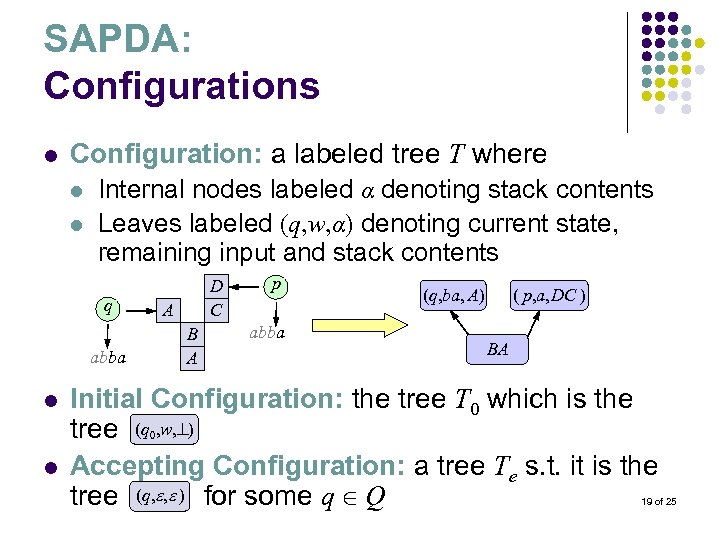SAPDA: Configurations l Configuration: a labeled tree T where l l Internal nodes labeled α denoting stack contents Leaves labeled (q, w, α) denoting current state, remaining input and stack contents q abba l l D C A B A p abba (q, ba, A) ( p, a, DC ) BA Initial Configuration: the tree T 0 which is the tree (q 0, w, ) Accepting Configuration: a tree Te s. t. it is the tree (q, , ) for some q Q 19 of 25

SAPDA: Computation l Computation: l l Each computation step, a transition is applied to one stack-branch If a stack-branch empties, it cannot be selected If all siblings branches are empty and “synchronized” then they are collapsed Synchronized Collapsing: All siblings… l l l Are empty Have the same state Have the same remaining input Are all labeled (q, w, ɛ) 20 of 25

SAPDA: Language l l l Accepting Computation: The final configuration is an accepting one, i. e. (q, , ) for some q Q. L(A) = {w * | A has an accepting computation on w} Note: Acceptance by accepting states can also be defined. Both models of acceptance are equivalent. 21 of 25

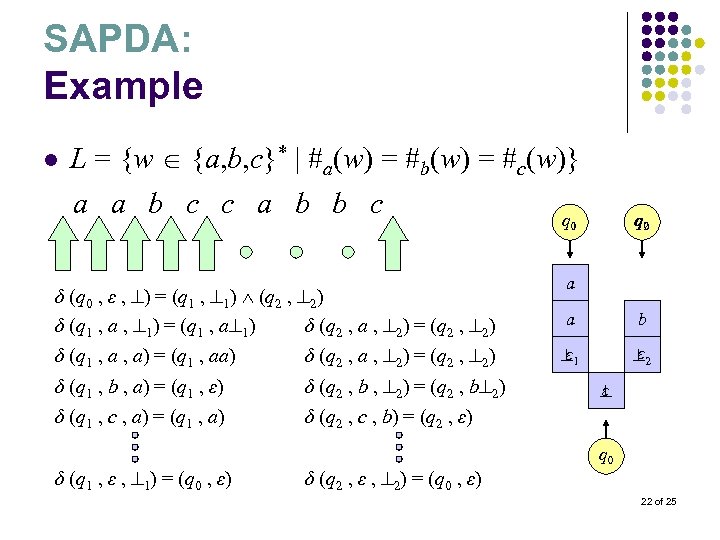SAPDA: Example l L = {w {a, b, c}* | #a(w) = #b(w) = #c(w)} a a b c c a b b c q q 2 0 0 1 δ (q 0 , ε , ) = (q 1 , 1) (q 2 , 2) δ (q 1 , a , 1) = (q 1 , a 1) δ (q 2 , a , 2) = (q 2 , 2) δ (q 1 , a) = (q 1 , aa) δ (q 2 , a , 2) = (q 2 , 2) δ (q 1 , b , a) = (q 1 , ε) δ (q 1 , c , a) = (q 1 , a) δ (q 1 , ε , 1) = (q 0 , ε) δ (q 2 , b , 2) = (q 2 , b 2) δ (q 2 , c , b) = (q 2 , ε) δ (q 2 , ε , 2) = (q 0 , ε) a a b ε 1 ε 2 ε q 0 22 of 25

Equivalence Results l l Theorem 1: SAPDA CG Theorem 2: CG 1 -state SAPDA (1 SAPDA) l Corollary 1: SAPDA ~ CG Corollary 2: SAPDA ~ 1 SAPDA l Proofs: l l l Both are extensions of the classical ones Surprisingly, the grammar-to-automaton translation is the more complicated one… 23 of 25

Future Directions l Linear CG and 1 -turn SAPDA l l It is well known that LCFG ~ 1 -turn PDA Linear CG: one non-terminal in each conjunct 1 -turn SAPDA: each stack-branch turns once Initial results point towards: 1 -turn SAPDA ~ LCG l Finite-turn SAPDA, Deterministic SAPDA… l Possibly, find a method to prove a language cannot be accepted by an SAPDA / CG… 24 of 25

Thank You