6729175bfdec7c53fe677297846eff8a.ppt
- Количество слайдов: 58
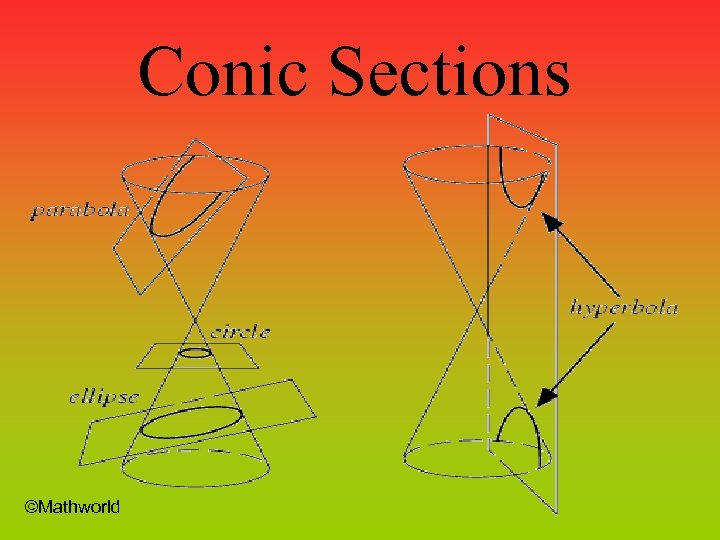 Conic Sections ©Mathworld
Conic Sections ©Mathworld
 Circle ©National Science Foundation
Circle ©National Science Foundation
 Circle • The Standard Form of a circle with a center at (0, 0) and a radius, r, is……. . center (0, 0) radius = 2 Copyright © 1999 -2004 Oswego City School District Regents Exam Prep Center
Circle • The Standard Form of a circle with a center at (0, 0) and a radius, r, is……. . center (0, 0) radius = 2 Copyright © 1999 -2004 Oswego City School District Regents Exam Prep Center
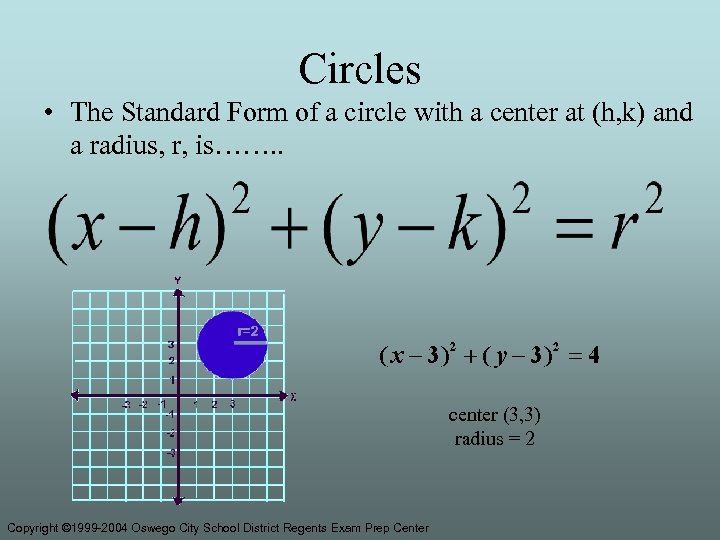 Circles • The Standard Form of a circle with a center at (h, k) and a radius, r, is……. . center (3, 3) radius = 2 Copyright © 1999 -2004 Oswego City School District Regents Exam Prep Center
Circles • The Standard Form of a circle with a center at (h, k) and a radius, r, is……. . center (3, 3) radius = 2 Copyright © 1999 -2004 Oswego City School District Regents Exam Prep Center
 Parabolas © Art Mayoff © Long Island Fountain Company
Parabolas © Art Mayoff © Long Island Fountain Company
 What’s in a Parabola • A parabola is the set of all points in a plane such that each point in the set is equidistant from a line called the directrix and a fixed point called the focus. Copyright © 1997 -2004, Math Academy Online™ / Platonic Realms™.
What’s in a Parabola • A parabola is the set of all points in a plane such that each point in the set is equidistant from a line called the directrix and a fixed point called the focus. Copyright © 1997 -2004, Math Academy Online™ / Platonic Realms™.
 Why is the focus so important? © Jill Britton, September 25, 2003
Why is the focus so important? © Jill Britton, September 25, 2003
 Parabola • The Standard Form of a Parabola that opens to the right and has a vertex at (0, 0) is…… © 1999 Addison Wesley Longman, Inc.
Parabola • The Standard Form of a Parabola that opens to the right and has a vertex at (0, 0) is…… © 1999 Addison Wesley Longman, Inc.
 Parabola • The Parabola that opens to the right and has a vertex at (0, 0) has the following characteristics…… • p is the distance from the vertex of the parabola to the focus or directrix • This makes the coordinates of the focus (p, 0) • This makes the equation of the directrix x = -p • The makes the axis of symmetry the x-axis (y = 0)
Parabola • The Parabola that opens to the right and has a vertex at (0, 0) has the following characteristics…… • p is the distance from the vertex of the parabola to the focus or directrix • This makes the coordinates of the focus (p, 0) • This makes the equation of the directrix x = -p • The makes the axis of symmetry the x-axis (y = 0)
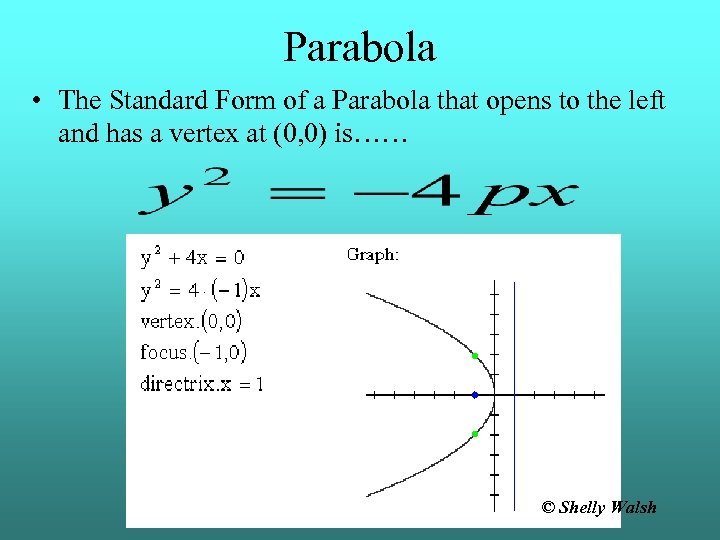 Parabola • The Standard Form of a Parabola that opens to the left and has a vertex at (0, 0) is…… © Shelly Walsh
Parabola • The Standard Form of a Parabola that opens to the left and has a vertex at (0, 0) is…… © Shelly Walsh
 Parabola • The Parabola that opens to the left and has a vertex at (0, 0) has the following characteristics…… • p is the distance from the vertex of the parabola to the focus or directrix • This makes the coordinates of the focus(-p, 0) • This makes the equation of the directrix x = p • The makes the axis of symmetry the x-axis (y = 0)
Parabola • The Parabola that opens to the left and has a vertex at (0, 0) has the following characteristics…… • p is the distance from the vertex of the parabola to the focus or directrix • This makes the coordinates of the focus(-p, 0) • This makes the equation of the directrix x = p • The makes the axis of symmetry the x-axis (y = 0)
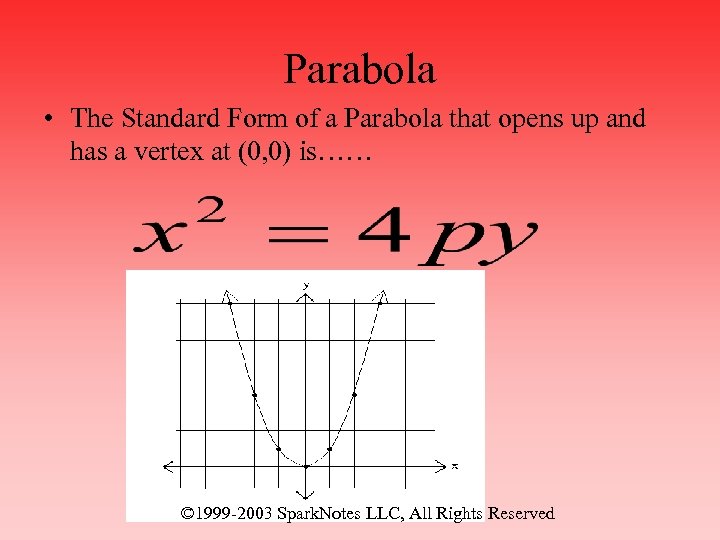 Parabola • The Standard Form of a Parabola that opens up and has a vertex at (0, 0) is…… © 1999 -2003 Spark. Notes LLC, All Rights Reserved
Parabola • The Standard Form of a Parabola that opens up and has a vertex at (0, 0) is…… © 1999 -2003 Spark. Notes LLC, All Rights Reserved
 Parabola • The Parabola that opens up and has a vertex at (0, 0) has the following characteristics…… • p is the distance from the vertex of the parabola to the focus or directrix • This makes the coordinates of the focus (0, p) • This makes the equation of the directrix y = -p • This makes the axis of symmetry the y-axis (x = 0)
Parabola • The Parabola that opens up and has a vertex at (0, 0) has the following characteristics…… • p is the distance from the vertex of the parabola to the focus or directrix • This makes the coordinates of the focus (0, p) • This makes the equation of the directrix y = -p • This makes the axis of symmetry the y-axis (x = 0)
 Parabola • The Standard Form of a Parabola that opens down and has a vertex at (0, 0) is…… © 1999 Addison Wesley Longman, Inc.
Parabola • The Standard Form of a Parabola that opens down and has a vertex at (0, 0) is…… © 1999 Addison Wesley Longman, Inc.
 Parabola • The Parabola that opens down and has a vertex at (0, 0) has the following characteristics…… • p is the distance from the vertex of the parabola to the focus or directrix • This makes the coordinates of the focus (0, -p) • This makes the equation of the directrix y = p • This makes the axis of symmetry the y-axis (x = 0)
Parabola • The Parabola that opens down and has a vertex at (0, 0) has the following characteristics…… • p is the distance from the vertex of the parabola to the focus or directrix • This makes the coordinates of the focus (0, -p) • This makes the equation of the directrix y = p • This makes the axis of symmetry the y-axis (x = 0)
 Parabola • The Standard Form of a Parabola that opens to the right and has a vertex at (h, k) is…… © Shelly Walsh
Parabola • The Standard Form of a Parabola that opens to the right and has a vertex at (h, k) is…… © Shelly Walsh
 Parabola • The Parabola that opens to the right and has a vertex at (h, k) has the following characteristics……. . • p is the distance from the vertex of the parabola to the focus or directrix • This makes the coordinates of the focus (h+p, k) • This makes the equation of the directrix x = h – p • This makes the axis of symmetry
Parabola • The Parabola that opens to the right and has a vertex at (h, k) has the following characteristics……. . • p is the distance from the vertex of the parabola to the focus or directrix • This makes the coordinates of the focus (h+p, k) • This makes the equation of the directrix x = h – p • This makes the axis of symmetry
 Parabola • The Standard Form of a Parabola that opens to the left and has a vertex at (h, k) is…… ©June Jones, University of Georgia
Parabola • The Standard Form of a Parabola that opens to the left and has a vertex at (h, k) is…… ©June Jones, University of Georgia
 Parabola • The Parabola that opens to the left and has a vertex at (h, k) has the following characteristics…… • p is the distance from the vertex of the parabola to the focus or directrix • This makes the coordinates of the focus (h – p, k) • This makes the equation of the directrix x = h + p • The makes the axis of symmetry
Parabola • The Parabola that opens to the left and has a vertex at (h, k) has the following characteristics…… • p is the distance from the vertex of the parabola to the focus or directrix • This makes the coordinates of the focus (h – p, k) • This makes the equation of the directrix x = h + p • The makes the axis of symmetry
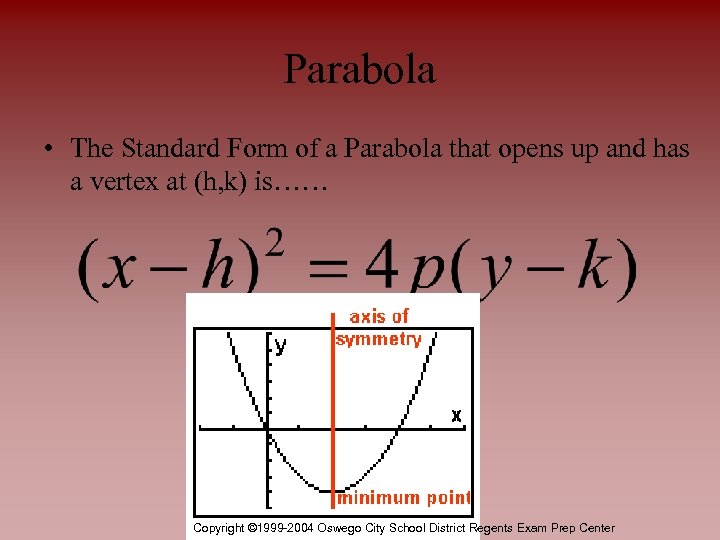 Parabola • The Standard Form of a Parabola that opens up and has a vertex at (h, k) is…… Copyright © 1999 -2004 Oswego City School District Regents Exam Prep Center
Parabola • The Standard Form of a Parabola that opens up and has a vertex at (h, k) is…… Copyright © 1999 -2004 Oswego City School District Regents Exam Prep Center
 Parabola • The Parabola that opens up and has a vertex at (h, k) has the following characteristics…… • p is the distance from the vertex of the parabola to the focus or directrix • This makes the coordinates of the focus (h , k + p) • This makes the equation of the directrix y = k – p • The makes the axis of symmetry
Parabola • The Parabola that opens up and has a vertex at (h, k) has the following characteristics…… • p is the distance from the vertex of the parabola to the focus or directrix • This makes the coordinates of the focus (h , k + p) • This makes the equation of the directrix y = k – p • The makes the axis of symmetry
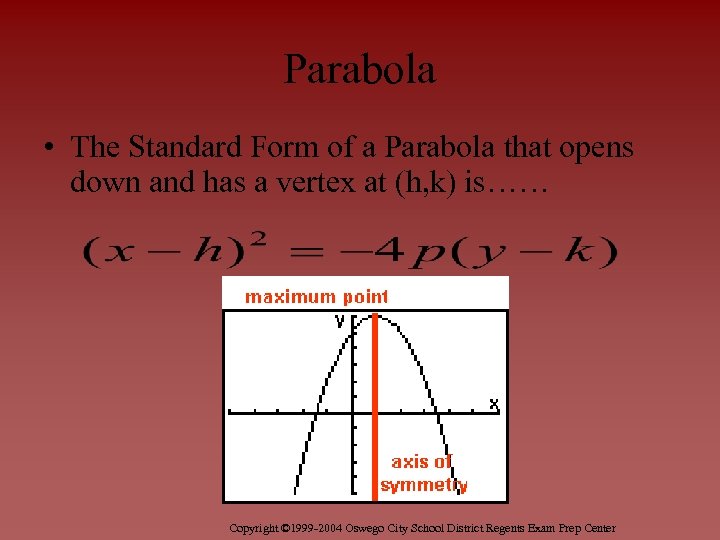 Parabola • The Standard Form of a Parabola that opens down and has a vertex at (h, k) is…… Copyright © 1999 -2004 Oswego City School District Regents Exam Prep Center
Parabola • The Standard Form of a Parabola that opens down and has a vertex at (h, k) is…… Copyright © 1999 -2004 Oswego City School District Regents Exam Prep Center
 Parabola • The Parabola that opens down and has a vertex at (h, k) has the following characteristics…… • p is the distance from the vertex of the parabola to the focus or directrix • This makes the coordinates of the focus (h , k - p) • This makes the equation of the directrix y = k + p • This makes the axis of symmetry
Parabola • The Parabola that opens down and has a vertex at (h, k) has the following characteristics…… • p is the distance from the vertex of the parabola to the focus or directrix • This makes the coordinates of the focus (h , k - p) • This makes the equation of the directrix y = k + p • This makes the axis of symmetry
 Ellipse © Jill Britton, September 25, 2003 • Statuary Hall in the U. S. Capital building is elliptic. It was in this room that John Quincy Adams, while a member of the House of Representatives, discovered this acoustical phenomenon. He situated his desk at a focal point of the elliptical ceiling, easily eavesdropping on the private conversations of other House members located near the other focal point.
Ellipse © Jill Britton, September 25, 2003 • Statuary Hall in the U. S. Capital building is elliptic. It was in this room that John Quincy Adams, while a member of the House of Representatives, discovered this acoustical phenomenon. He situated his desk at a focal point of the elliptical ceiling, easily eavesdropping on the private conversations of other House members located near the other focal point.
 What is in an Ellipse? • The set of all points in the plane, the sum of whose distances from two fixed points, called the foci, is a constant. (“Foci” is the plural of “focus”, and is pronounced FOH-sigh. ) • Copyright © 1997 -2004, Math Academy Online™ / Platonic Realms™.
What is in an Ellipse? • The set of all points in the plane, the sum of whose distances from two fixed points, called the foci, is a constant. (“Foci” is the plural of “focus”, and is pronounced FOH-sigh. ) • Copyright © 1997 -2004, Math Academy Online™ / Platonic Realms™.
 Why are the foci of the ellipse important? • The ellipse has an important property that is used in the reflection of light and sound waves. Any light or signal that starts at one focus will be reflected to the other focus. This principle is used in lithotripsy, a medical procedure for treating kidney stones. The patient is placed in a elliptical tank of water, with the kidney stone at one focus. High-energy shock waves generated at the other focus are concentrated on the stone, pulverizing it.
Why are the foci of the ellipse important? • The ellipse has an important property that is used in the reflection of light and sound waves. Any light or signal that starts at one focus will be reflected to the other focus. This principle is used in lithotripsy, a medical procedure for treating kidney stones. The patient is placed in a elliptical tank of water, with the kidney stone at one focus. High-energy shock waves generated at the other focus are concentrated on the stone, pulverizing it.
 Why are the foci of the ellipse important? • St. Paul's Cathedral in London. If a person whispers near one focus, he can be heard at the other focus, although he cannot be heard at many places in between. © 1994 -2004 Kevin Matthews and Artifice, Inc. All Rights Reserved.
Why are the foci of the ellipse important? • St. Paul's Cathedral in London. If a person whispers near one focus, he can be heard at the other focus, although he cannot be heard at many places in between. © 1994 -2004 Kevin Matthews and Artifice, Inc. All Rights Reserved.
 Ellipse • General Rules – – – x and y are both squared Equation always equals(=) 1 Equation is always plus(+) a 2 is always the biggest denominator c 2 = a 2 – b 2 c is the distance from the center to each foci on the major axis – The center is in the middle of the 2 vertices, the 2 covertices, and the 2 foci.
Ellipse • General Rules – – – x and y are both squared Equation always equals(=) 1 Equation is always plus(+) a 2 is always the biggest denominator c 2 = a 2 – b 2 c is the distance from the center to each foci on the major axis – The center is in the middle of the 2 vertices, the 2 covertices, and the 2 foci.
 Ellipse • General Rules – a is the distance from the center to each vertex on the major axis – b is the distance from the center to each vertex on the minor axis (co-vertices) – Major axis has a length of 2 a – Minor axis has a length of 2 b – Eccentricity(e): e = c/a (The closer e gets to 1, the closer it is to being circular)
Ellipse • General Rules – a is the distance from the center to each vertex on the major axis – b is the distance from the center to each vertex on the minor axis (co-vertices) – Major axis has a length of 2 a – Minor axis has a length of 2 b – Eccentricity(e): e = c/a (The closer e gets to 1, the closer it is to being circular)
 Ellipse • The standard form of the ellipse with a center at (0, 0) and a horizontal axis is……
Ellipse • The standard form of the ellipse with a center at (0, 0) and a horizontal axis is……
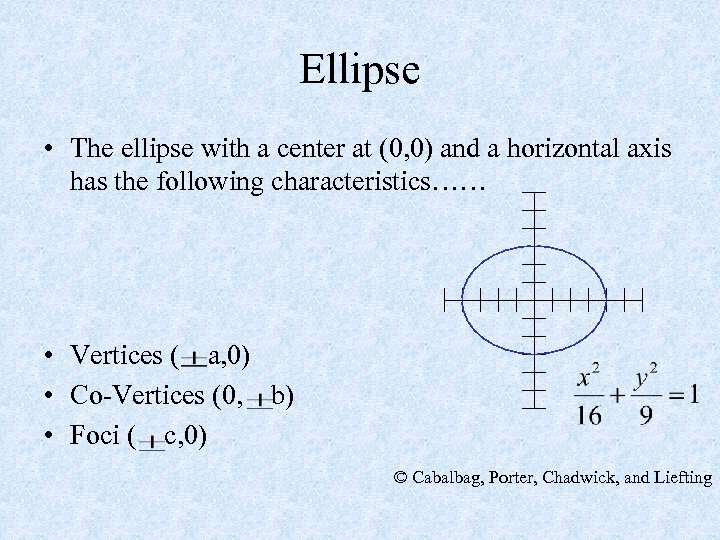 Ellipse • The ellipse with a center at (0, 0) and a horizontal axis has the following characteristics…… • Vertices ( a, 0) • Co-Vertices (0, b) • Foci ( c, 0) © Cabalbag, Porter, Chadwick, and Liefting
Ellipse • The ellipse with a center at (0, 0) and a horizontal axis has the following characteristics…… • Vertices ( a, 0) • Co-Vertices (0, b) • Foci ( c, 0) © Cabalbag, Porter, Chadwick, and Liefting
 Ellipse • The standard form of the ellipse with a center at (0, 0) and a vertical axis is……
Ellipse • The standard form of the ellipse with a center at (0, 0) and a vertical axis is……
 Ellipse • The ellipse with a center at (0, 0) and a vertical axis has the following characteristics…… • Vertices (0, a) • Co-Vertices ( b, 0) • Foci (0, c) © Cabalbag, Porter, Chadwick, and Liefting
Ellipse • The ellipse with a center at (0, 0) and a vertical axis has the following characteristics…… • Vertices (0, a) • Co-Vertices ( b, 0) • Foci (0, c) © Cabalbag, Porter, Chadwick, and Liefting
 Ellipse • The standard form of the ellipse with a center at (h, k) and a horizontal axis is……
Ellipse • The standard form of the ellipse with a center at (h, k) and a horizontal axis is……
 Ellipse • The ellipse with a center at (h, k) and a horizontal axis has the following characteristics…… • Vertices (h a , k) • Co-Vertices (h, k b) • Foci (h c , k) ©Sellers, James
Ellipse • The ellipse with a center at (h, k) and a horizontal axis has the following characteristics…… • Vertices (h a , k) • Co-Vertices (h, k b) • Foci (h c , k) ©Sellers, James
 Ellipse • The standard form of the ellipse with a center at (h, k) and a vertical axis is……
Ellipse • The standard form of the ellipse with a center at (h, k) and a vertical axis is……
 Ellipse • The ellipse with a center at (h, k) and a vertical axis has the following characteristics…… • Vertices (h, k a) • Co-Vertices (h b , k) • Foci (h, k c) © Joan Bookbinder 1998 -2000
Ellipse • The ellipse with a center at (h, k) and a vertical axis has the following characteristics…… • Vertices (h, k a) • Co-Vertices (h b , k) • Foci (h, k c) © Joan Bookbinder 1998 -2000
 Hyperbola © Jill Britton, September 25, 2003 The huge chimney of a nuclear power plant has the shape of a hyperboloid, as does the architecture of the James S. Mc. Donnell Planetarium of the St. Louis Science Center.
Hyperbola © Jill Britton, September 25, 2003 The huge chimney of a nuclear power plant has the shape of a hyperboloid, as does the architecture of the James S. Mc. Donnell Planetarium of the St. Louis Science Center.
 What is a Hyperbola? • The set of all points in the plane, the difference of whose distances from two fixed points, called the foci, remains constant. Copyright © 1997 -2004, Math Academy Online™ / Platonic Realms™.
What is a Hyperbola? • The set of all points in the plane, the difference of whose distances from two fixed points, called the foci, remains constant. Copyright © 1997 -2004, Math Academy Online™ / Platonic Realms™.
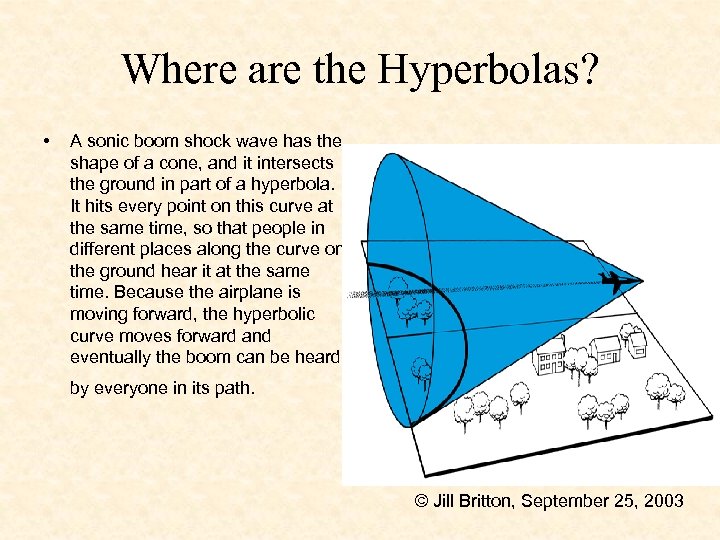 Where are the Hyperbolas? • A sonic boom shock wave has the shape of a cone, and it intersects the ground in part of a hyperbola. It hits every point on this curve at the same time, so that people in different places along the curve on the ground hear it at the same time. Because the airplane is moving forward, the hyperbolic curve moves forward and eventually the boom can be heard by everyone in its path. © Jill Britton, September 25, 2003
Where are the Hyperbolas? • A sonic boom shock wave has the shape of a cone, and it intersects the ground in part of a hyperbola. It hits every point on this curve at the same time, so that people in different places along the curve on the ground hear it at the same time. Because the airplane is moving forward, the hyperbolic curve moves forward and eventually the boom can be heard by everyone in its path. © Jill Britton, September 25, 2003
 Hyperbola • General Rules – – – x and y are both squared Equation always equals(=) 1 Equation is always minus(-) a 2 is always the first denominator c 2 = a 2 + b 2 c is the distance from the center to each foci on the major axis – a is the distance from the center to each vertex on the major axis
Hyperbola • General Rules – – – x and y are both squared Equation always equals(=) 1 Equation is always minus(-) a 2 is always the first denominator c 2 = a 2 + b 2 c is the distance from the center to each foci on the major axis – a is the distance from the center to each vertex on the major axis
 Hyperbola • General Rules – b is the distance from the center to each midpoint of the rectangle used to draw the asymptotes. This distance runs perpendicular to the distance (a). – Major axis has a length of 2 a – Eccentricity(e): e = c/a (The closer e gets to 1, the closer it is to being circular – If x 2 is first then the hyperbola is horizontal – If y 2 is first then the hyperbola is vertical.
Hyperbola • General Rules – b is the distance from the center to each midpoint of the rectangle used to draw the asymptotes. This distance runs perpendicular to the distance (a). – Major axis has a length of 2 a – Eccentricity(e): e = c/a (The closer e gets to 1, the closer it is to being circular – If x 2 is first then the hyperbola is horizontal – If y 2 is first then the hyperbola is vertical.
 Hyperbola • General Rules – – The center is in the middle of the 2 vertices and the 2 foci. The vertices and the covertices are used to draw the rectangles that form the asymptotes. The vertices and the covertices are the midpoints of the rectangle The covertices are not labeled on the hyperbola because they are not actually part of the graph
Hyperbola • General Rules – – The center is in the middle of the 2 vertices and the 2 foci. The vertices and the covertices are used to draw the rectangles that form the asymptotes. The vertices and the covertices are the midpoints of the rectangle The covertices are not labeled on the hyperbola because they are not actually part of the graph
 Hyperbola • The standard form of the Hyperbola with a center at (0, 0) and a horizontal axis is……
Hyperbola • The standard form of the Hyperbola with a center at (0, 0) and a horizontal axis is……
 Hyperbola • The Hyperbola with a center at (0, 0) and a horizontal axis has the following characteristics…… • • Vertices ( a, 0) Foci ( c, 0) • Asymptotes:
Hyperbola • The Hyperbola with a center at (0, 0) and a horizontal axis has the following characteristics…… • • Vertices ( a, 0) Foci ( c, 0) • Asymptotes:
 Hyperbola • The standard form of the Hyperbola with a center at (0, 0) and a vertical axis is……
Hyperbola • The standard form of the Hyperbola with a center at (0, 0) and a vertical axis is……
 Hyperbola • The Hyperbola with a center at (0, 0) and a vertical axis has the following characteristics…… • • Vertices (0, a) Foci ( 0, c) • Asymptotes:
Hyperbola • The Hyperbola with a center at (0, 0) and a vertical axis has the following characteristics…… • • Vertices (0, a) Foci ( 0, c) • Asymptotes:
 Hyperbola • The standard form of the Hyperbola with a center at (h, k) and a horizontal axis is……
Hyperbola • The standard form of the Hyperbola with a center at (h, k) and a horizontal axis is……
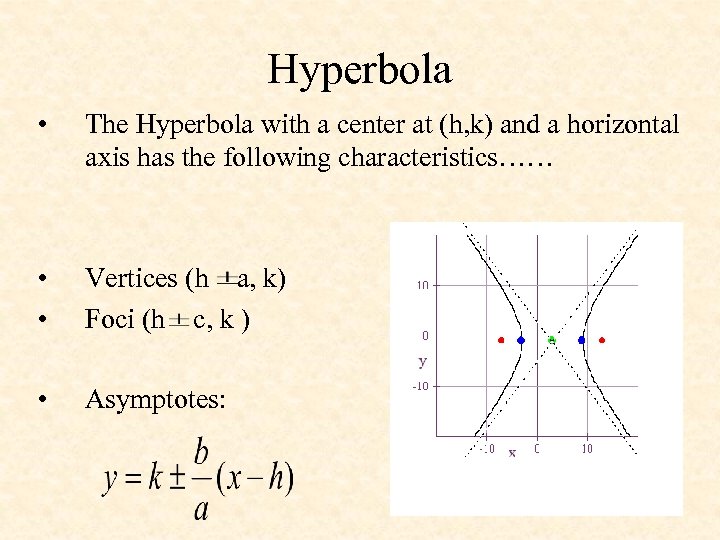 Hyperbola • The Hyperbola with a center at (h, k) and a horizontal axis has the following characteristics…… • • Vertices (h a, k) Foci (h c, k ) • Asymptotes:
Hyperbola • The Hyperbola with a center at (h, k) and a horizontal axis has the following characteristics…… • • Vertices (h a, k) Foci (h c, k ) • Asymptotes:
 Hyperbola • The standard form of the Hyperbola with a center at (h, k) and a vertical axis is……
Hyperbola • The standard form of the Hyperbola with a center at (h, k) and a vertical axis is……
 Hyperbola • The Hyperbola with a center at (h, k) and a vertical axis has the following characteristics…… • • Vertices (h, k a) Foci (h, k c) • Asymptotes: ©Sellers, James
Hyperbola • The Hyperbola with a center at (h, k) and a vertical axis has the following characteristics…… • • Vertices (h, k a) Foci (h, k c) • Asymptotes: ©Sellers, James
 Rotating the Coordinate Axis © James Wilson
Rotating the Coordinate Axis © James Wilson
 Equations for Rotating the Coordinate Axes
Equations for Rotating the Coordinate Axes
 Resources Bookbinder, John. Unit 8: Conic Sections (College Algebra Online). 2000. June 3, 2004
Resources Bookbinder, John. Unit 8: Conic Sections (College Algebra Online). 2000. June 3, 2004
 Resources Finney, Ross, et. al. Calculus: Graphical, Numerical, Algebraic. Scott Foresman-Addison Wesley, 1999. Jones, June. Instructional Unit on Conic Sections. University of Georgia. June 3, 2004 http: //jwilson. coe. uga. edu/emt 669/Student. Folders/Jones. June/conic s/conics. html Mathews, Kevin. Great Buildings Online. Great Buildings. une 3, 2004
Resources Finney, Ross, et. al. Calculus: Graphical, Numerical, Algebraic. Scott Foresman-Addison Wesley, 1999. Jones, June. Instructional Unit on Conic Sections. University of Georgia. June 3, 2004 http: //jwilson. coe. uga. edu/emt 669/Student. Folders/Jones. June/conic s/conics. html Mathews, Kevin. Great Buildings Online. Great Buildings. une 3, 2004
 Resources Mayoff, Art. San Francisco and the Golden Gate Bridge. June 3, 2004 http: //mathworld. wolfram. com/Conic. Section. html>. Mueller, William. Modeling Periodicity. June 3, 2004
Resources Mayoff, Art. San Francisco and the Golden Gate Bridge. June 3, 2004 http: //mathworld. wolfram. com/Conic. Section. html>. Mueller, William. Modeling Periodicity. June 3, 2004
 Resources Quadratics. Spark Notes from Barnes and Noble. June 3, 2004
Resources Quadratics. Spark Notes from Barnes and Noble. June 3, 2004
 Resources Walsh, Shelly. Chapter 9 (Precalculus). June 3, 2004 http: //faculty. ed. umuc. edu/~swalsh/UM/M 108 Ch 9. html Weissteing, Eric W. "Conic Section. " From Math. World--A Wolfram Web Resource. http: //mathworld. wolfram. com/Conic. Section. html Wilson, James W. CURVE BUILDING. An Exploration with Algebraic Relations University of Georgia. June 3, 2004 http: //jwilson. coe. uga. edu/Texts. Folder/cb/curve. building. html
Resources Walsh, Shelly. Chapter 9 (Precalculus). June 3, 2004 http: //faculty. ed. umuc. edu/~swalsh/UM/M 108 Ch 9. html Weissteing, Eric W. "Conic Section. " From Math. World--A Wolfram Web Resource. http: //mathworld. wolfram. com/Conic. Section. html Wilson, James W. CURVE BUILDING. An Exploration with Algebraic Relations University of Georgia. June 3, 2004 http: //jwilson. coe. uga. edu/Texts. Folder/cb/curve. building. html
