Confidence Intervals for Capture Recapture Data With Matching

Confidence Intervals for Capture. Recapture Data With Matching Stephen Sharp, National Records of Scotland

The Problem (i) • You have undertaken a (presumably imperfect) enumeration of a given population. • You then undertaken a second (also presumably imperfect) coverage survey. • You have matched the two so that you know how many people were in both surveys (N 12); in the first survey only (N 1); and in the second survey only (N 2). • You require to estimate the number of people in neither survey (N 0).

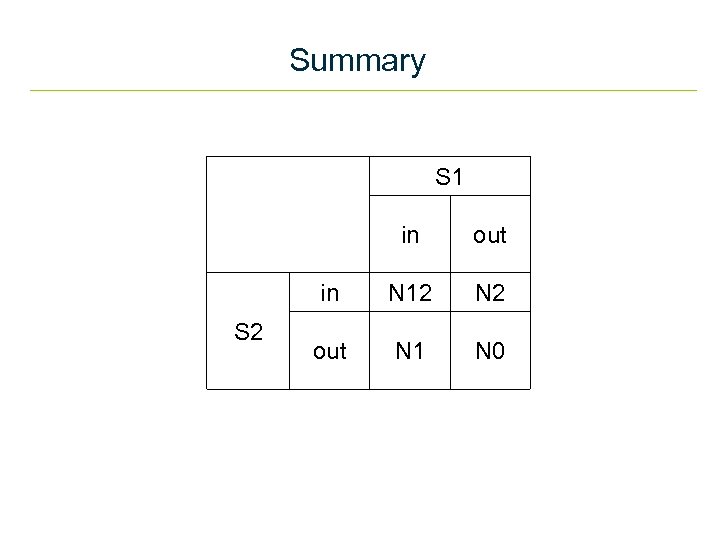Summary S 1 out in S 2 in N 12 N 2 out N 1 N 0

The Problem (ii) • The classical estimate of N 0 is the product of N 1 and N 2 divided by N 12. • However this assumes that absence from the first survey does not change the probability of absence from the second. • For humans, this is very unlikely.

A Bayesian approach • As we do not know N 0, we require its probability distribution conditional on N 12, N 1 and N 2 which we do know. • We get this from Bayes’ theorem. • p(N 0 | N 12 N 1 N 2) = constant x p(N 12 N 1 N 2 | N 0) x p(N 0). • Posterior is proportional to likelihood x prior. • We need a likelihood and a prior.

The likelihood function (i) • The distribution of N 12, N 1 and N 2 conditional on N 0 is multinomial with probability parameters p 12, p 1, p 2 and p 0. • The four probabilities must sum to one so we need three constraints to specify uniquely three parameters. • We assume that p 12, p 1 and p 2 stand in the same proportions as N 12, N 1 and N 2. • This gives us two constraints.

The likelihood function (ii) • Instead of imposing a third constraint however we let the posterior distribution of N 0 depend on the dichotomous correlation ϕ, which measures stochastic dependency. • We can now specify the likelihood for a given value of ϕ and watch the effect of changing it.

The prior distribution • What did we know about the likely size of the population before we took the two surveys? • This knowledge is reflected in the prior distribution. • A safe bet would be an uninformative prior (perhaps a normal or uniform distribution with a very big variance). • If you are confident though you might be better to use an informative prior (i. e. a smaller prior variance). • This reduces the variance of the posterior distribution (though be careful to check that the prior is consistent with the likelihood).

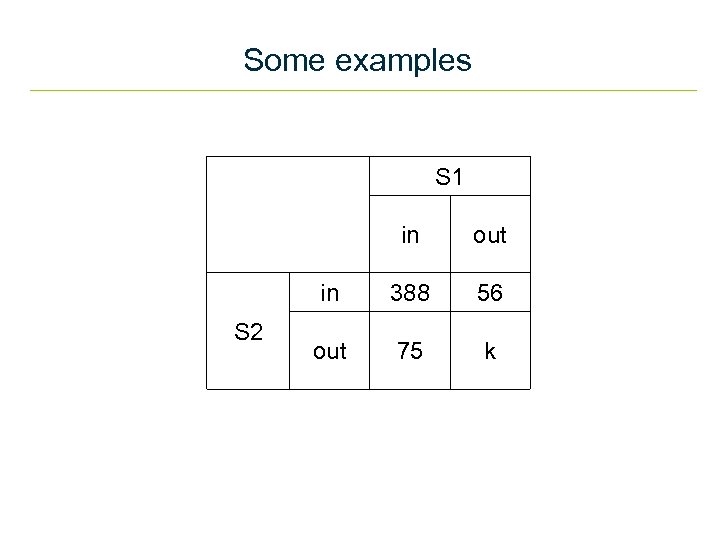Some examples S 1 out in S 2 in 388 56 out 75 k

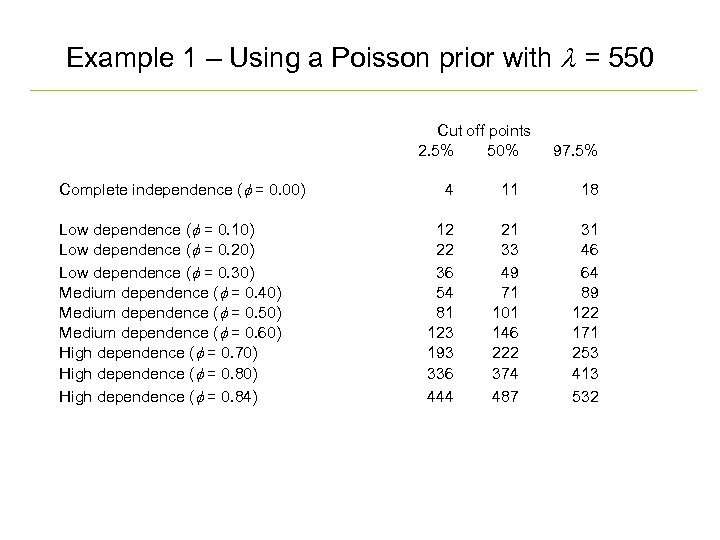Example 1 – Using a Poisson prior with l = 550 Complete independence (f = 0. 00) Low dependence (f = 0. 10) Low dependence (f = 0. 20) Low dependence (f = 0. 30) Medium dependence (f = 0. 40) Medium dependence (f = 0. 50) Medium dependence (f = 0. 60) High dependence (f = 0. 70) High dependence (f = 0. 84) Cut off points 2. 5% 50% 97. 5% 4 11 18 12 22 36 54 81 123 193 336 444 21 33 49 71 101 146 222 374 487 31 46 64 89 122 171 253 413 532

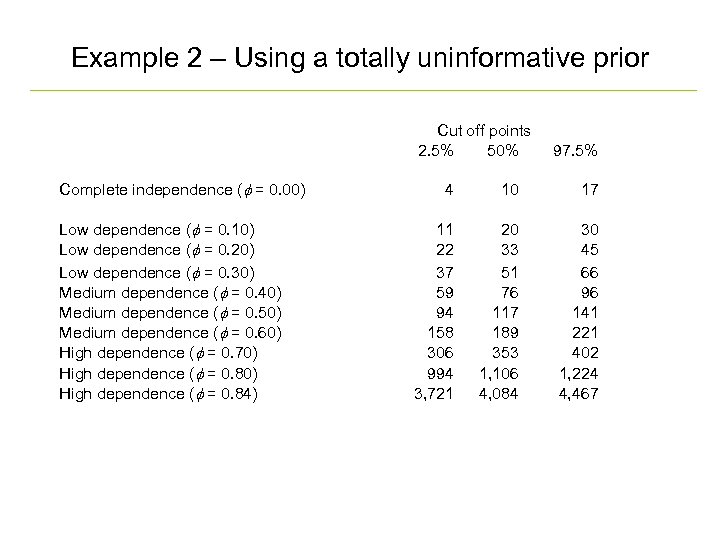Example 2 – Using a totally uninformative prior Complete independence (f = 0. 00) Low dependence (f = 0. 10) Low dependence (f = 0. 20) Low dependence (f = 0. 30) Medium dependence (f = 0. 40) Medium dependence (f = 0. 50) Medium dependence (f = 0. 60) High dependence (f = 0. 70) High dependence (f = 0. 84) Cut off points 2. 5% 50% 97. 5% 4 10 17 11 22 37 59 94 158 306 994 3, 721 20 33 51 76 117 189 353 1, 106 4, 084 30 45 66 96 141 221 402 1, 224 4, 467

Further work (i) • So we can model the point estimate and confidence intervals as a function of the dichotomous correlation f. • But what is the value of f? • This will vary from one subgroup to another within the population. • It will depend on the diversity within the subgroup of the propensity to take part in public surveys like the Census and the coverage survey.

Further work (ii) • Attempts to model this have suggested that typical values for f vary between 0. 25 and 0. 40. • This suggests that for an uninformative prior, the population point estimate might be 560 against 520 with the independence assumption; an underestimate of about 7%. • The confidence intervals are ± 14 or 15 as opposed to ± 6 or 7; about twice as wide.

Conclusion • The assumption of independence introduces error into both the point estimate and the confidence intervals when population size is estimated from capture-recapture data. • The CI error is in the “wrong” direction (i. e. not on the side of caution). • Departure from independence arises because those members of the population unlikely to be included in one sample are less likely to be included in the other. • Assessing the extent of dependence is difficult but its effects make it important to try.

Confidence Intervals for Capture-Recapture Data With Matching Stephen Sharp National Records of Scotland Ladywell House Ladywell Road Edinburgh EH 12 7 TF 0131 314 4649 Stephen. sharp@gro-scotland. gsi. gov. uk