Conditional Dependencies Wenfei Fan University of Edinburgh and Bell Laboratories 1
Outline of Part III ü Conditional functional dependencies (CFDs) – Motivation for extending FDs with conditions: data cleaning – Syntax and semantics – Static analysis: satisfiability, implication, axiomatizability ü Conditional inclusion dependencies (CINDs) – Motivation: data cleaning and schema matching – Syntax and semantics – Static analysis: satisfiability, implication, axiomatizability ü Algorithms and open research issues – SQL techniques for inconsistency detection – Heuristic for satisfiability and implication checking – Repair 2
Conditional functional dependencies (CFDs) ü Conditional functional dependencies (CFDs) – Motivation for extending FDs with conditions: data cleaning – Syntax and semantics – Static analysis: satisfiability, implication, axiomatizability ü Conditional inclusion dependencies (CINDs) – Motivation: data cleaning and schema matching – Syntax and semantics – Static analysis: consistency, implication, axiomatizability ü Algorithms and open research issues – SQL techniques for inconsistency detection – Heuristic for satisfiability and implication checking – Repair 3
Data in real-life is often dirty Errors, conflicts and inconsistencies ü Australia: 500, 000 dead people retain active Medicare cards ü US: Pentagon asked 275 dead/wounded officers to re-enlist. ü UK: there are 81 million National Insurance numbers but only 60 million eligible citizens. ü It is estimated that in a 500, 000 customer database, 120, 000 customer records become invalid within a year, due to deaths, divorces, marriages, moves. ü typical data error rate in industry: 1% - 5%, up to 30% ü. . . 4
Dirty data is costly ü Poor data costs US companies $600 billion annually ü Wrong price data in retail databases costs US customers $2. 5 billion each year ü AAA improves data quality by 20%, and saves $150, 000… in postage stamps alone ü 30%-80% of the development time for data cleaning in a data integration project and don’t forget ü CIA intelligence on WMD in Iraq! The need for (semi-)automated methods to clean data! 5
Characterizing the consistency of data ü One of the central technical problems is how to tell whether the data is dirty or clean ü Specify consistency using integrity constraints Inconsistencies emerge as violations of constraints ü Constraints considered so far: traditional – – functional dependencies inclusion dependencies denial constraints (a special case of full dependencies). . . Question: are these traditional dependencies sufficient? 6
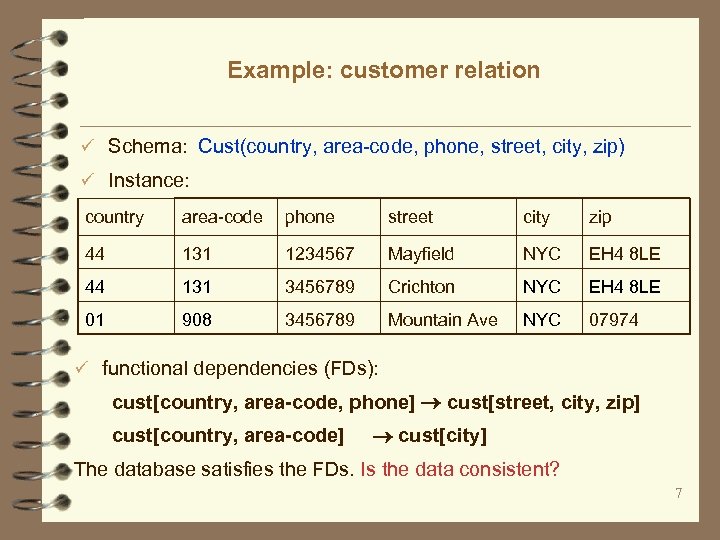
Example: customer relation ü Schema: Cust(country, area-code, phone, street, city, zip) ü Instance: country area-code phone street city zip 44 131 1234567 Mayfield NYC EH 4 8 LE 44 131 3456789 Crichton NYC EH 4 8 LE 01 908 3456789 Mountain Ave NYC 07974 ü functional dependencies (FDs): cust[country, area-code, phone] cust[street, city, zip] cust[country, area-code] cust[city] The database satisfies the FDs. Is the data consistent? 7
![Capturing inconsistencies in the data ü cust ([country = 44, zip] [street]) In the](https://present5.com/presentation/046fa2dd2ce19a6405587f0c9c181c15/image-8.jpg "Capturing inconsistencies in the data ü cust ([country = 44, zip] [street]) In the")
Capturing inconsistencies in the data ü cust ([country = 44, zip] [street]) In the UK, zip code uniquely determines the street The constraint may not hold for other countries ü It expresses a fundamental part of the semantics of the data ü It can NOT be expressed as a traditional FD – It does not hold on the entire relation; instead, it holds on tuples representing UK customers only country area-code phone street city zip 44 131 1234567 Mayfield NYC EH 4 8 LE 44 131 3456789 Crichton NYC EH 4 8 LE 01 908 3456789 Mountain Ave NYC 07974 8
![Two more constraints cust([country = 44, area-code = 131, phone] [street, zip, city =](https://present5.com/presentation/046fa2dd2ce19a6405587f0c9c181c15/image-9.jpg "Two more constraints cust([country = 44, area-code = 131, phone] [street, zip, city =")
Two more constraints cust([country = 44, area-code = 131, phone] [street, zip, city = EDI]) cust([country = 01, area-code = 908, phone] [street, zip, city = MH]) – In the UK, if the area code is 131, then the city has to be EDI – In the US, if the area code is 908, then the city has to be MH ü t 1, t 2 and t 3 violate these constraints – refining cust([country, area-code, phno] [street, city, zip]) – combining constants and variables id country Area-code phone street city zip t 1 44 131 1234567 Mayfield NYC EH 4 8 LE t 2 44 131 3456789 Crichton NYC EH 4 8 LE t 3 01 908 3456789 Mountain Ave NYC 07974 9
![The need for new constraints cust([country = 44, zip] [street]) cust([country = 44, area-code](https://present5.com/presentation/046fa2dd2ce19a6405587f0c9c181c15/image-10.jpg "The need for new constraints cust([country = 44, zip] [street]) cust([country = 44, area-code")
The need for new constraints cust([country = 44, zip] [street]) cust([country = 44, area-code = 131, phone] [street, zip, city = EDI]) cust([country = 01, area-code = 908, phone] [street, zip, city = MH]) ü They capture inconsistencies that traditional FDs cannot detect Traditional constraints were developed for schema design, not for data cleaning! ü Data integration in real-life: source constraints – hold on a subset of sources – hold conditionally on the integrated data ü They are NOT expressible as traditional FDs – do not hold on the entire relation – contain constant data values, besides logical variables 10
Conditional Functional Dependencies (CFDs) An extension of traditional FDs: (R: X Y, Tp) ü X Y: embedded traditional FD on R ü Tp: a pattern tableau – attributes: X Y – each tuple in Tp consists of constants and unnamed variable _ Example: cust([country = 44, zip] [street]) ü (cust (country, zip street), Tp) ü pattern tableau Tp country zip street 44 _ _ 11
![Example CFDs Represent cust([country = 44, area-code = 131, phone] [street, zip, city =](https://present5.com/presentation/046fa2dd2ce19a6405587f0c9c181c15/image-12.jpg "Example CFDs Represent cust([country = 44, area-code = 131, phone] [street, zip, city =")
Example CFDs Represent cust([country = 44, area-code = 131, phone] [street, zip, city = EDI]) cust([country = 01, area-code = 908, phone] [street, zip, city = MH]) cust([country, area-code, phone] [street, city, zip]) as a SINGLE CFD: ü (cust(country, area-code, phone street, city, zip), Tp) ü pattern tableau Tp: one tuple for each constraint country area-code phone street city zip 44 131 _ _ Edi _ 01 908 _ _ MH _ _ _ _ 12
![Traditional FDs as a special case Express cust[country, area-code] cust[city] as a CFD: ü](https://present5.com/presentation/046fa2dd2ce19a6405587f0c9c181c15/image-13.jpg "Traditional FDs as a special case Express cust[country, area-code] cust[city] as a CFD: ü")
Traditional FDs as a special case Express cust[country, area-code] cust[city] as a CFD: ü (cust(country, area-code, city), Tp) ü pattern tableau Tp: a single tuple consisting of _ only country area-code _ _ city _ CFDs subsume traditional FDs 13
Semantics of CFDs ü a b (a matches b) if – either a or b is _ – both a and b are constants and a = b ü tuple t 1 matches t 2: t 1 t 2 (a, b) (a, _), but (a, b) does not match (a, c) ü DB satisfies (R: X Y, Tp) iff for any tuple tp in the pattern tableau Tp and for any tuples t 1, t 2 in DB, if t 1[X] = t 2[X] tp[X], then t 1[Y] = t 2[Y] tp[Y] – tp[X]: identifying the set of tuples on which the constraint tp applies, ie, { t | t[X] tp[X]} – t 1[Y] = t 2[Y] tp[Y]: enforcing the embedded FD, and the pattern of tp 14
![Example: violation of CFDs cust([country = 44, zip] [street]) Tuples t 1 and t](https://present5.com/presentation/046fa2dd2ce19a6405587f0c9c181c15/image-15.jpg "Example: violation of CFDs cust([country = 44, zip] [street]) Tuples t 1 and t")
Example: violation of CFDs cust([country = 44, zip] [street]) Tuples t 1 and t 2 violate the CFD country zip street 44 _ _ ü t 1[country, zip] = t 2[country, zip] tp[country, zip] ü t 1[street] t 2[street] The CFD applies to t 1 and t 2 since they match tp[country, zip] id country area-code phone street city zip t 1 44 131 1234567 Mayfield NYC EH 4 8 LE t 2 44 131 3456789 Crichton NYC EH 8 8 LE t 3 01 908 3456789 Mountain Ave NYC 07974 15
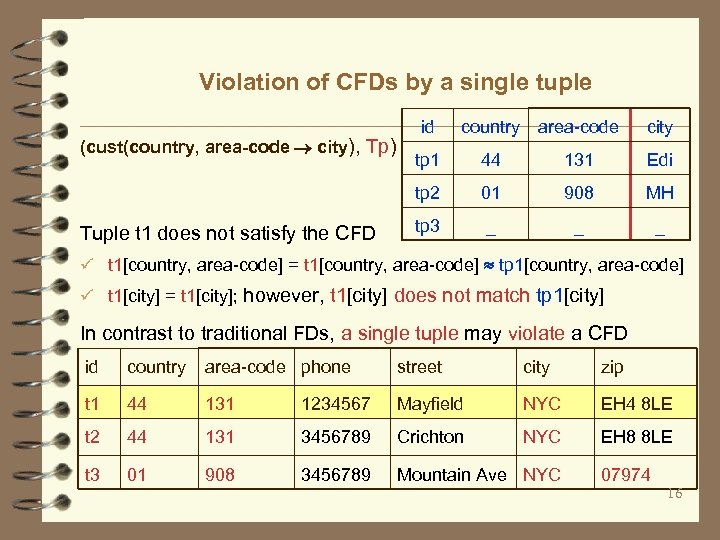
Violation of CFDs by a single tuple Tuple t 1 does not satisfy the CFD country area-code city tp 1 44 131 Edi tp 2 (cust(country, area-code city), Tp) id 01 908 MH tp 3 _ _ _ ü t 1[country, area-code] = t 1[country, area-code] tp 1[country, area-code] ü t 1[city] = t 1[city]; however, t 1[city] does not match tp 1[city] In contrast to traditional FDs, a single tuple may violate a CFD id country area-code phone street city zip t 1 44 131 1234567 Mayfield NYC EH 4 8 LE t 2 44 131 3456789 Crichton NYC EH 8 8 LE t 3 01 908 3456789 Mountain Ave NYC 07974 16
CFDs vs. conditional tables Conditional tables, Codd tables and variable tables have been studied for incomplete information ü Conditional tables: representing infinitely many relation instances, one for each instantiation of variables ü Pattern tableau in a CFD: each pattern tuple is a constraint, and all constraints applying to the same relation instance Relational table, traditional dependencies and CFDs ü One end of the spectrum: relations consisting of data only ü The other end of the spectrum: traditional dependencies defined in terms of logic variables ü CFD: in the between, both data values and logic variables CFDs: enforcing binding of semantically related data values 17
“Dirty” constraints? id A set of CFDs may be inconsistent! ü Inconsistent: (R(A B), Tp) Tp A B tp 1 _ b tp 2 _ c In any nonempty database DB and for any tuple t in DB, – tp 1: t[B] must be b – tp 2: t[B] must be c – Inconsistent if b and c are different ü inconsistent = { 1, 2 }, 1 = (R(A B), Tp 1), 2 = (R(B A), Tp 2) id B A tp 1 Why? A true b tp 3 b false tp 2 false c tp 4 c true 18
The satisfiability problem ü The satisfiability problem for CFDs is to determine, given a set of CFDs, whether or not there exists a nonempty database DB that satisfies , i. e. , for any in , DB satisfies . Whether or not makes sense ü For traditional FDs, it is not an issue: one can specify any FDs without worrying about their consistency ü In contrast, a set of CFDs may be inconsistent! 19
The complexity of the satisfiability analysis Theorem. The satisfiability problem for CFDs is NP-complete. Nontrivial: contrast this with the trivial consistency analysis of FDs! Proof idea: ü Upper bound: the small model property: if is satisfiable, then there is DB that satisfies and consists of a single tuple! ü Lower bound: reduction from the non-tautology problem Good news: PTIME special cases Theorem. Given a set of CFDs on a relation schema R, the satisfiability of can be determined in O(| |2) time if either ü the schema R is predefined (fixed), or ü no attributes in have a finite domain Proof idea: an extension of chase for CFDs 20
The implication problem for CFDs is to determine, given a set of CFDs and a single CFD , whether implies , denoted by |= , i. e. , for any database DB, if DB satisfies , then DB satisfies . Example: ü = { 1, 2 } , 1 = (R(A B), Tp 1), Tp 1 id A B tp 1 _ b ü = (R(A C), Tp) 2 = (R(B C), Tp 2) id B C tp 1 Tp 2 _ c id A C tp a c ü |= . Why? 21
The complexity of the implication problem ü For traditional FDs, the implication problem is in linear time ü In contrast, the implication problem for CFDs is intractable Theorem. The implication problem for CFDs is co. NP-complete. Tractable special cases Theorem. Given a set of CFDs and a single CFD on a relation schema R, whether |= can be determined in O((| | + | |)2) time if either ü the schema R is predefined, or ü no attributes in and have a finite domain Proof idea: an extension of chase for CFDs 22
Finite axiomatizability: Flashback Armstrong’s axioms can be found in every database textbook: ü Reflexivity: If Y X, then X Y ü Augmentation: If X Y , then XZ YZ ü Transitivity: If X Y and Y Z, then X Z Sound and complete for FD implication, i. e, |= iff can be inferred from using reflexivity, augmentation, transitivity. Question: is there a sound and complete inference system for the implication analysis of CFDs? 23
Finite axiomatizability of CFDs Theorem. There is a sound and complete inference system I for implication analysis of CFDs ü Sound: if |- , i. e. , can be proved from using I, then |= ü Complete: if |= , then |- using I The inference system is more involved than its counterpart for traditional FDs, namely, Armstrong’s axioms. There are 5 axioms. A normal form of CFDs: (R: X A, tp), tp is a single pattern tuple. 24
Axioms for CFDs: extension of Armstrong’s axioms ü Reflexivity: If A X, then (R : X A, tp), where A 1 … Ak A A _ … _ _ _ A 1 … Ak A A _ … _ a a or ü Augmentation: If (X A, tp) and B attr(R), then (BX A, t’p) A 1 … Ak A A 1 … Ak B A tp[A 1] … tp[Ak] _ tp[A] tp t’p 25
![Axioms for CFDs: transitivity Transitivity: if ([A 1, …, Ak] [B 1, …, Bm],](https://present5.com/presentation/046fa2dd2ce19a6405587f0c9c181c15/image-26.jpg "Axioms for CFDs: transitivity Transitivity: if ([A 1, …, Ak] [B 1, …, Bm],")
Axioms for CFDs: transitivity Transitivity: if ([A 1, …, Ak] [B 1, …, Bm], tp) A 1 … Ak B 1 tp[A 1] … tp[Ak] tp[B 1] and ([B 1, …, Bm] [C 1, …, Cn], t’p) … Bm tp[Bm] match B 1 … Bm C 1 tp’[B 1] … t’p[Bm] t’p[C 1] A 1 … Ak C 1 tp[A 1] … tp[Ak] … Cn t’p[Cm] … t’p[C 1] ([A 1, …, Ak] [C 1, …, Cn], t’p) Cn t’p[Cn] 26
![Axioms for CFDs: reduction ü reduction: if ([B, X] A, tp), tp[B] = _,](https://present5.com/presentation/046fa2dd2ce19a6405587f0c9c181c15/image-27.jpg "Axioms for CFDs: reduction ü reduction: if ([B, X] A, tp), tp[B] = _,")
Axioms for CFDs: reduction ü reduction: if ([B, X] A, tp), tp[B] = _, and tp[A] = a A 1 Ak B A tp[A 1] then (X A, t’p) … … tp[Ak] _ a A 1 … Ak A tp[A 1] … tp[Ak] a 27
Axioms for CFDs: finite domain upgrade ü upgrade: if only consistent values for B are b 1, b 2, . . . , bn, dom(B) = { b 1, …, bn, …, bm}, and (R : [A 1, . . . , Ak, B] A, tp) A 1 … Ak B A tp[A 1] … tp[Ak] b 1 tp[A] tp[A 1] … tp[Ak] … tp[A] tp[A 1] … tp[Ak] bn tp[A] then (R : [A 1, . . . , Ak, B] A, tp) A 1 … Ak B A tp[A 1] … tp[Ak] _ tp[A] 28
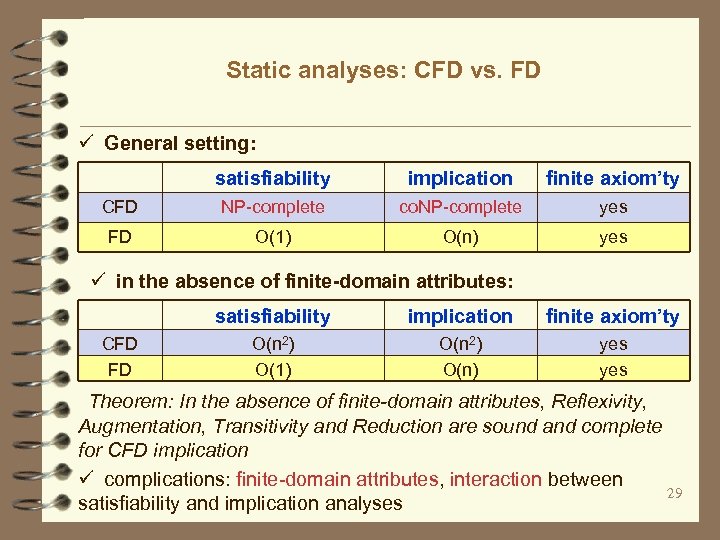
Static analyses: CFD vs. FD ü General setting: satisfiability implication finite axiom’ty CFD NP-complete co. NP-complete yes FD O(1) O(n) yes ü in the absence of finite-domain attributes: satisfiability CFD FD implication finite axiom’ty O(n 2) O(1) O(n 2) O(n) yes Theorem: In the absence of finite-domain attributes, Reflexivity, Augmentation, Transitivity and Reduction are sound and complete for CFD implication ü complications: finite-domain attributes, interaction between 29 satisfiability and implication analyses
Conditional Inclusion dependencies (CINDs) ü Conditional functional dependencies (CFDs) – Motivation for extending FDs with conditions: data cleaning – Syntax and semantics – Static analysis: satisfiability, implication, axiomatizability ü Conditional inclusion dependencies (CINDs) – Motivation: data cleaning and schema matching – Syntax and semantics – Static analysis: consistency, implication, axiomatizability ü Algorithms and open research issues – SQL techniques for inconsistency detection – Heuristic for satisfiability and implication checking – Repair 30
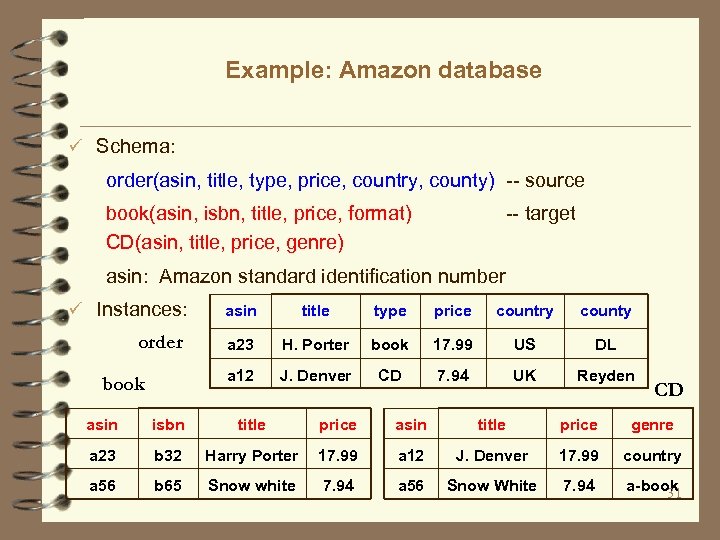
Example: Amazon database ü Schema: order(asin, title, type, price, country, county) -- source book(asin, isbn, title, price, format) CD(asin, title, price, genre) -- target asin: Amazon standard identification number ü Instances: book title type price country county a 23 H. Porter book 17. 99 US DL a 12 order asin J. Denver CD 7. 94 UK Reyden CD asin isbn title price asin title price genre a 23 b 32 Harry Porter 17. 99 a 12 J. Denver 17. 99 country a 56 b 65 Snow white 7. 94 a 56 Snow White 7. 94 a-book 31
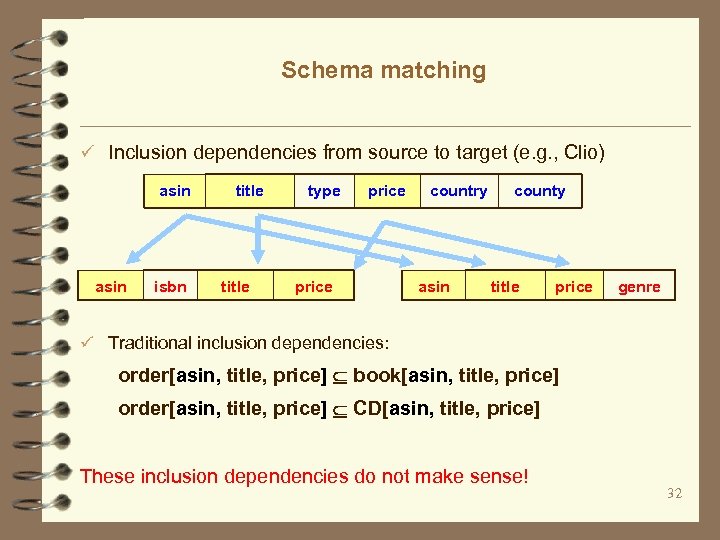
Schema matching ü Inclusion dependencies from source to target (e. g. , Clio) asin isbn title type price country asin county title price genre ü Traditional inclusion dependencies: order[asin, title, price] book[asin, title, price] order[asin, title, price] CD[asin, title, price] These inclusion dependencies do not make sense! 32
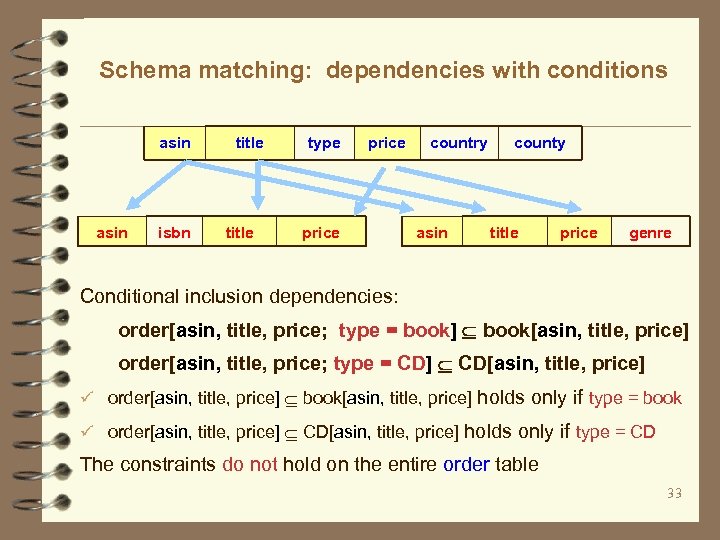
Schema matching: dependencies with conditions asin isbn title type price country asin county title price genre Conditional inclusion dependencies: order[asin, title, price; type = book] book[asin, title, price] order[asin, title, price; type = CD] CD[asin, title, price] ü order[asin, title, price] book[asin, title, price] holds only if type = book ü order[asin, title, price] CD[asin, title, price] holds only if type = CD The constraints do not hold on the entire order table 33
![Date cleaning with conditional dependencies CIND 1: order[asin, title, price; type = book] book[asin,](https://present5.com/presentation/046fa2dd2ce19a6405587f0c9c181c15/image-34.jpg "Date cleaning with conditional dependencies CIND 1: order[asin, title, price; type = book] book[asin,")
Date cleaning with conditional dependencies CIND 1: order[asin, title, price; type = book] book[asin, title, price] CIND 2: order[asin, title, price; type = CD] CD[asin, title, price] ü Tuple t 1 violates CIND 1 ü Tuple t 2 violates CIND 2 asin title type price country county t 1 a 23 H. Porter book 17. 99 US DL t 2 order id a 12 J. Denver CD 7. 94 UK Reyden CD book asin isbn title price asin title price genre a 23 b 32 Harry Porter 17. 99 a 12 J. Denver 17. 99 country a 56 b 65 Snow white 7. 94 a 56 Snow White 7. 94 a-book 34
More on data cleaning CD asin title price genre a 12 J. Denver 17. 99 country a 56 Snow White 7. 94 a-book asin isbn title price format a 23 b 32 Harry Porter 17. 99 Hard cover a 56 book b 65 Snow White 17. 94 audio CD[asin, title, price; genre = ‘a-book’] book[asin, title, price; format = ‘audio’] ü Inclusion relation CD[asin, title, price] book[asin, title, price] holds only if genre = ‘a-book’, i. e. , when the CD is an audio book ü In addition, the format of the corresponding book must be audio – a pattern for the referenced tuple 35
![Conditional Inclusion Dependencies (CINDs) (R 1[X; Xp] R 2[Y; Yp], Tp) ü R 1[X]](https://present5.com/presentation/046fa2dd2ce19a6405587f0c9c181c15/image-36.jpg "Conditional Inclusion Dependencies (CINDs) (R 1[X; Xp] R 2[Y; Yp], Tp) ü R 1[X]")
Conditional Inclusion Dependencies (CINDs) (R 1[X; Xp] R 2[Y; Yp], Tp) ü R 1[X] R 2[Y]: embedded traditional IND from R 1 to R 2 ü Tp: a pattern tableau – attributes: X Xp Y Yp – tuples in Tp consist of constants and unnamed variable _ Example: express CIND 1: order[asin, title, price; type = book] book[asin, title, price] ü (order[asin, title, price; type] book[asin, title, price; nil], Tp) nil: empty list ü pattern tableau Tp asin title price type asin title price _ _ _ book _ _ _ 36
![Examples CIND 2: order[asin, title, price; type = CD] CD[asin, title, price] CIND 3:](https://present5.com/presentation/046fa2dd2ce19a6405587f0c9c181c15/image-37.jpg "Examples CIND 2: order[asin, title, price; type = CD] CD[asin, title, price] CIND 3:")
Examples CIND 2: order[asin, title, price; type = CD] CD[asin, title, price] CIND 3: CD[asin, title, price; genre = ‘a-book’] book[asin, title, price; format = ‘audio’] ü (order[asin, title, price; type] CD[asin, title, price; nil], Tp) asin title price type asin title price _ _ _ CD _ _ _ ü (CD[asin, title, price; genre] book[asin, title, price; format], Tp) asin title price genre asin title price format _ _ _ a-book _ _ _ audio 37
![Traditional CINDs as a special case R 1[X] R 2[Y] ü X: [A 1,](https://present5.com/presentation/046fa2dd2ce19a6405587f0c9c181c15/image-38.jpg "Traditional CINDs as a special case R 1[X] R 2[Y] ü X: [A 1,")
Traditional CINDs as a special case R 1[X] R 2[Y] ü X: [A 1, …, An] ü Y : [B 1, …, Bn] As a CIND: (R 1[X; nil] R 2[Y; nil], Tp) ü pattern tableau Tp: a single tuple consisting of _ only A 1 … An B 1 … Bn _ _ _ CINDs subsume traditional INDs 38
Semantics of CINDs DB = (DB 1, DB 2), where DBj is an instance of Rj, j = 1, 2. DB satisfies (R 1[X; Xp] R 2[Y; Yp], Tp) iff for any tuples t 1 in DB 1, and any tuple tp in the pattern tableau Tp, if t 1[X, Xp] tp[X, Xp], then there exists t 2 in DB 2 such that ü t 1[Y] = t 2[Y] (traditional IND semantics) ü t 2[Y, Yp] tp[Y, Yp] (matching the pattern tuple on Y, Yp) Patterns: ü t 1[X, Xp] tp[X, Xp]: identifying the set of R 1 tuples on which tp applies: { t 1 | t 1[X, Xp] tp[X, Xp] } ü t 2[Y, Yp] tp[Y, Yp]: enforcing the embedded IND and the constraint specified by patterns Y, Yp 39
![Example (CD[asin, title, price; genre] book[asin, title, price; format], Tp) asin title price genre](https://present5.com/presentation/046fa2dd2ce19a6405587f0c9c181c15/image-40.jpg "Example (CD[asin, title, price; genre] book[asin, title, price; format], Tp) asin title price genre")
Example (CD[asin, title, price; genre] book[asin, title, price; format], Tp) asin title price genre asin title price format _ _ _ a-book _ _ _ audio The following DB satisfies the CIND CD isbn title price format a 23 b 32 Harry Porter 17. 99 Hard cover a 56 book asin b 65 Snow white 7. 94 audio asin title price genre a 12 J. Denver 17. 99 country a 56 Snow White 7. 94 a-book 40
![More examples CIND 1: (order[asin, title, price; type] book[asin, title, price; nil], Tp) asin](https://present5.com/presentation/046fa2dd2ce19a6405587f0c9c181c15/image-41.jpg "More examples CIND 1: (order[asin, title, price; type] book[asin, title, price; nil], Tp) asin")
More examples CIND 1: (order[asin, title, price; type] book[asin, title, price; nil], Tp) asin title price type asin title price _ _ _ book _ _ _ The following DB violates CIND 1. Why? id title type price country county t 1 a 23 H. Porter book 17. 99 US DL t 2 order asin a 12 J. Denver CD 7. 94 UK Reyden book CD asin isbn title price asin title price genre a 23 b 32 Harry Porter 17. 99 a 12 J. Denver 17. 99 country a 56 b 65 Snow white 7. 94 a 56 S. White 7. 94 a-book 41
The satisfiability problem for CINDs is to determine, given a set of CINDs, whether or not there exists a nonempty database DB that satisfies , i. e. , for any in , DB satisfies . Recall ü Any set of traditional INDs is always satisfiable! ü For CFDs, the satisfiability problem is intractable. In contrast. Theorem. Any set of CINDs is always satisfiable! Despite the increased expressive power, the complexity of the satisfiability analysis does not go up. 42
The implication problem for CINDs is to decide, given a set of CINDs and a single CIND , whether implies ( |= ). ü For traditional INDs, the implication problem is PS PACE-complete ü For CINDs, the complexity does not hike up, to an extent: Theorem. For CINDs containing no finite-domain attributes, the implication problem is PSPACE-complete In the general setting, however, we have to pay a price: Theorem. The implication problem for CINDs is EXPTIME-complete Proof idea: ü Lower bound: reduction from two-player tiling game ü Upper bound: an extension of the chase for CINDs 43
![Finite axiomatizability of CINDs ü Rules for inferring IND implication: – Reflexivity: If R[X]](https://present5.com/presentation/046fa2dd2ce19a6405587f0c9c181c15/image-44.jpg "Finite axiomatizability of CINDs ü Rules for inferring IND implication: – Reflexivity: If R[X]")
Finite axiomatizability of CINDs ü Rules for inferring IND implication: – Reflexivity: If R[X] – Projection and Permutation: If R 1[A 1, …, Ak] R 2[B 1, …, Bk], then R 1[Ai 1, …, Aik] R 2[Bi 1, …, Bik], – Transitivity: If R 1[X] R 2[Y] and R 2[Y] R 3[Z], then R 1[X] R 3[Z] Sound and complete for IND implication ü CINDs retain the finite axiomatizability Theorem. There is a sound and complete inference system for implication analysis of CINDs There are 8 axioms. 44
![Inference rules for CINDs Normal form of CINDs: (R 1[X; Xp] R 2[Y; Yp],](https://present5.com/presentation/046fa2dd2ce19a6405587f0c9c181c15/image-45.jpg "Inference rules for CINDs Normal form of CINDs: (R 1[X; Xp] R 2[Y; Yp],")
Inference rules for CINDs Normal form of CINDs: (R 1[X; Xp] R 2[Y; Yp], tp), ü tp is a single pattern tuple ü tp[A] is a constant iff A is in Xp or Yp (tp[B] = _ if B is in X or Y) Inference rules ü Reflexivity: (R[X; nil] R[X; nil], tp), where A 1 … Ak _ … _ ü Projection and permutation: If (R 1[X; Xp] R 2[Y; Yp], tp), then (R 1[X’; X’p] R 2[Y’; Y’p], t’p), for any permutation of X, Xp X Xp Y Yp X’ X’p Y’ Y’p _ tp[Xp] _ tp[Yp] _ tp[X’p] _ tp[Y’p] tp t’p 45
![Axioms for CINDs: transitivity Transitivity: if (R 1[X; Xp] R 2[Y; Yp], tp), X](https://present5.com/presentation/046fa2dd2ce19a6405587f0c9c181c15/image-46.jpg "Axioms for CINDs: transitivity Transitivity: if (R 1[X; Xp] R 2[Y; Yp], tp), X")
Axioms for CINDs: transitivity Transitivity: if (R 1[X; Xp] R 2[Y; Yp], tp), X Xp Y Yp _ tp[Xp] _ tp[Yp] equal and (R 2[Y; Yp] R 3[Z; Zp], t’p), Y Yp Z Zp _ tp[Yp] _ t’p[Zp] X Xp Z Zp _ tp[Xp] _ t’p[Zp] (R 1[X; Xp] R 3[Z; Zp], t”p) 46
![Axioms for CINDs: downgrading ü downgrading: if (R 1[X, A; Xp] R 2[Y, B;](https://present5.com/presentation/046fa2dd2ce19a6405587f0c9c181c15/image-47.jpg "Axioms for CINDs: downgrading ü downgrading: if (R 1[X, A; Xp] R 2[Y, B;")
Axioms for CINDs: downgrading ü downgrading: if (R 1[X, A; Xp] R 2[Y, B; Yp], tp), X A Xp Y B Yp _ _ tp[Xp] _ _ tp[Yp] X Xp A Y Yp B _ tp[Xp] a _ tp[Yp] a (R 1[X; Xp, A] R 2[Y; Yp, B], t’p) 47
![Axioms for CINDs: augmentation ü augmentation: if (R 1[X; Xp] R 2[Y; Yp], tp),](https://present5.com/presentation/046fa2dd2ce19a6405587f0c9c181c15/image-48.jpg "Axioms for CINDs: augmentation ü augmentation: if (R 1[X; Xp] R 2[Y; Yp], tp),")
Axioms for CINDs: augmentation ü augmentation: if (R 1[X; Xp] R 2[Y; Yp], tp), A attr(R 1), X Xp Y Yp _ tp[Xp] _ tp[Yp] X Xp A Y Yp _ tp[Xp] a _ tp[Yp] (R 1[X; Xp, A] R 2[Y; Yp], t’p) 48
![Axioms for CINDs: reduction ü reduction: if (R 1[X; Xp] R 2[Y; Yp, B],](https://present5.com/presentation/046fa2dd2ce19a6405587f0c9c181c15/image-49.jpg "Axioms for CINDs: reduction ü reduction: if (R 1[X; Xp] R 2[Y; Yp, B],")
Axioms for CINDs: reduction ü reduction: if (R 1[X; Xp] R 2[Y; Yp, B], tp), X Xp Y Yp B _ tp[Xp] _ tp[Yp] tp[B] then (R 1[X; Xp] R 2[Y; Yp], t’p), X Xp Y Yp _ tp[Xp] _ tp[Yp] 49
![Axioms for CFDs: finite domain reduction ü F-reduction: if (R 1[X; Xp, A] R](https://present5.com/presentation/046fa2dd2ce19a6405587f0c9c181c15/image-50.jpg "Axioms for CFDs: finite domain reduction ü F-reduction: if (R 1[X; Xp, A] R")
Axioms for CFDs: finite domain reduction ü F-reduction: if (R 1[X; Xp, A] R 2[Y; Yp], tp), dom(A) = { a 1, …, an} X Xp A Y Yp _ tp[Xp] a 1 _ tp[Yp] _ tp[Xp] … _ tp[Yp] _ tp[Xp] an _ tp[Yp] then (R 1[X; Xp] R 2[Y; Yp], tp), X Xp Y Yp _ tp[Xp] _ tp[Yp] 50
![Axioms for CFDs: finite domain upgrade ü upgrade: if (R 1[X; Xp, A] R](https://present5.com/presentation/046fa2dd2ce19a6405587f0c9c181c15/image-51.jpg "Axioms for CFDs: finite domain upgrade ü upgrade: if (R 1[X; Xp, A] R")
Axioms for CFDs: finite domain upgrade ü upgrade: if (R 1[X; Xp, A] R 2[Y, B; Yp], tp), dom(A) = { a 1, …, an} X Xp A Y Yp B _ tp[Xp] a 1 _ tp[Yp] a 1 _ tp[Xp] … _ tp[Yp] … _ tp[Xp] an _ tp[Yp] an then (R 1[X, A; Xp] R 2[Y, B; Yp], tp), X A Xp Y B Yp _ _ tp[Xp] _ _ tp[Yp] 51
Static analyses: CIND vs. IND ü General setting: satisfiability implication finite axiom’ty CIND O(1) EXPTIME-complete yes IND O(1) PSPACE-complete yes ü in the absence of finite-domain attributes: satisfiability CIND implication finite axiom’ty O(1) PSPACE-complete yes Theorem: In the absence of finite-domain attributes, Reflexivity, Projection and Permutation, Transitivity, Augmentation, Downgrading and Reduction are sound and complete for CIND implication 52 CINDs retain most complexity bounds of their traditional counterpart
CFDs and CINDs taken together We need both CFDs and CINDs for ü data cleaning ü schema matching Theorem. The implication problem for CFDs and CINDs is undecidable Not surprising: The implication problem for traditional FDs and INDs is already undecidable Theorem. The consistency problem for CFDs and CINDs is undecidable In contrast, any set of traditional FDs and INDs is consistent! Proof idea: induction from the implication problem for FDs and INDs 53
Static analyses: CFD + CIND vs. FD + IND satisfiability implication finite axiom’ty CFD + CIND undecidable No FD + IND O(1) undecidable No ü CINDs and CFDs properly subsume FDs and INDs ü Both the satisfiability analysis and implication analysis are beyond reach in practice This calls for effective heuristic methods 54
Algorithms and open research issues ü Conditional functional dependencies (CFDs) – Motivation for extending FDs with conditions: data cleaning – Syntax and semantics – Static analysis: satisfiability, implication, axiomatizability ü Conditional inclusion dependencies (CINDs) – Motivation: data cleaning and schema matching – Syntax and semantics – Static analysis: consistency, implication, axiomatizability ü Algorithms and open research issues – SQL techniques for inconsistency detection – Heuristic for satisfiability and implication checking – Repair 55
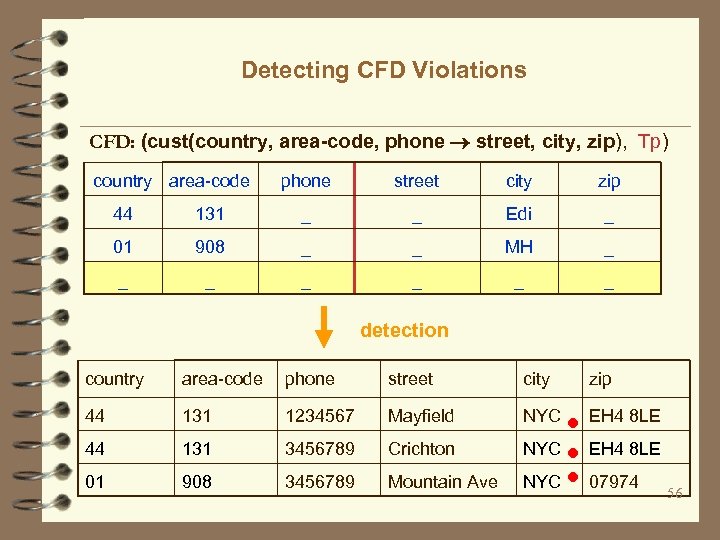
Detecting CFD Violations CFD: (cust(country, area-code, phone street, city, zip), Tp) country area-code phone street city zip 44 131 _ _ Edi _ 01 908 _ _ MH _ _ _ _ detection country area-code phone street city zip 44 131 1234567 Mayfield NYC EH 4 8 LE 44 131 3456789 Crichton NYC EH 4 8 LE 01 908 3456789 Mountain Ave NYC 07974 56
Detecting CFD violations ü Input: a set of CFDs and a database DB ü Output: the set of tuples in DB that violate at least one CFD in Approach: automatically generate SQL queries to find violations Complication 1: consider (R: X Y, Tp), the pattern tableau may be large (recall that each tuple in Tp is in fact a constraint) Goal: the size of the SQL queries is independent of Tp Trick: treat Tp as a data table CINDs can be checked along the same lines 57
Single CFD: step 1 A pair of SQL queries, treating Tp as a data table – Single-tuple violation (pattern matching) – Multi-tuple violations (traditional FDs) (cust(country, area-code, phone street, city, zip), Tp) ü Single-tuple violation: Qc select * from R t, Tp tp where t[country] tp[country] AND t[area-code] tp[area-code] AND t[phone] tp[phone] (t[street] <> tp[street] OR t[city] <> tp[city] OR t[zip] <> tp[zip])) – <>: not matching; – t[A 1] tp[A 1]: (t[A 1] = tp[A 1] OR tp[A 1] = _) 58
Single CFD: step 2 (cust(country, area-code, phone street, city, zip), Tp) ü Multi-tuple violations (the semantics of traditional FDs): Qv select distinct t. country, t. area-code, t. phone from R t, Tp tp where t[country] tp[country] AND t[area-code] tp[area-code] AND t[phone] tp[phone] group by t. country, t. area-code, t. phone having count(distinct street, city, zip) > 1 Tp is treated as a data table 59
Multiple CFDs Complication 2: if the set has n CFDs, do we use 2 n SQL queries, and thus 2 n passes of the database DB? Goal: ü 2 SQL queries no matter how many CFDs are in ü the size of the SQL queries is independent of Tp Trick: merge multiple CFDs into one ü Given (R: X 1 Y 1, Tp 1), (R: X 2 Y 2, Tp 2) ü Create a single pattern table: Tm = X 1 X 2 Y 1 Y 2, ü Introduce @, a don’t-care variable, to populate attributes of pattern tuples in X 1 – X 2, etc (tp[A] = @) ü Modify the pair of SQL queries by using Tm 60
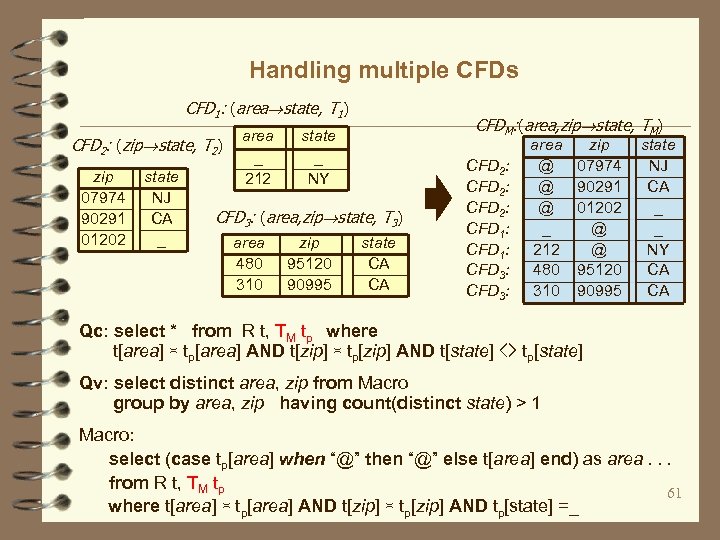
Handling multiple CFDs CFD 1: (area state, T 1) CFD 2: (zip state, T 2) zip 07974 90291 01202 state NJ CA _ area _ 212 CFDM: (area, zip state, TM) state _ NY CFD 3: (area, zip state, T 3) area 480 310 zip 95120 90995 state CA CA CFD 2: CFD 1: CFD 3: area @ @ @ _ 212 480 310 zip 07974 90291 01202 @ @ 95120 90995 state NJ CA _ _ NY CA CA Qc: select * from R t, TM tp where t[area] ≍ tp[area] AND t[zip] ≍ tp[zip] AND t[state] <> tp[state] Qv: select distinct area, zip from Macro group by area, zip having count(distinct state) > 1 Macro: select (case tp[area] when “@” then “@” else t[area] end) as area. . . from R t, TM tp 61 where t[area] ≍ tp[area] AND t[zip] ≍ tp[zip] AND tp[state] =_
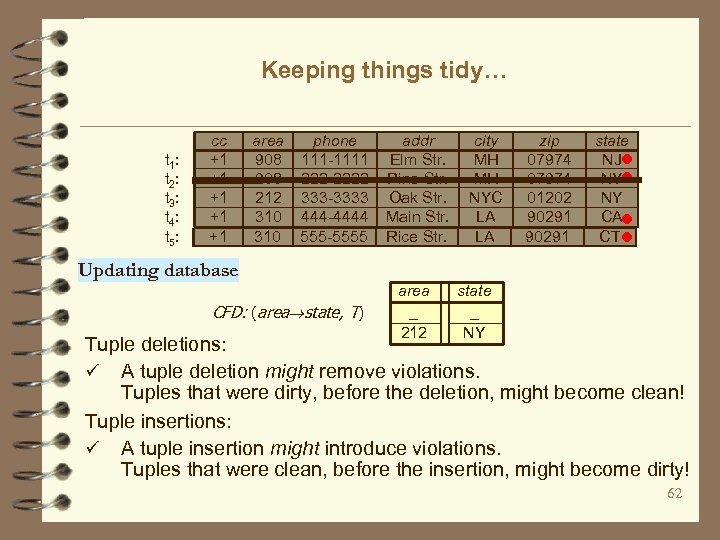
Keeping things tidy… t 1: t 2: t 3: t 4: t 5: cc +1 +1 +1 area 908 212 310 phone 111 -1111 222 -2222 333 -3333 444 -4444 555 -5555 Updating database CFD: (area state, T) addr Elm Str. Pine Str. Oak Str. Main Str. Rice Str. area _ 212 city MH MH NYC LA LA zip 07974 01202 90291 state NJ NY NY CA CT state _ NY Tuple deletions: ü A tuple deletion might remove violations. Tuples that were dirty, before the deletion, might become clean! Tuple insertions: ü A tuple insertion might introduce violations. Tuples that were clean, before the insertion, might become dirty! 62
Incremental inconsistency detection ü Input: a set of CFDs, a database DB, the set V of tuples in DB that violate , and changes DB to DB ü Output: the set V’ of tuples in DB + DB that violate CFDs in DB: a set of tuples to be inserted into DB or deleted from DB Approaches: ü Batch approach: – Compute DB’ = DB + DB – Apply the SQL detection queries to DB’ ü Incremental approach: compute change V such that the new violations V’ = the old violations V + V Why? 63
The need for incremental inconsistency detection ü Small DB to DB tends to incur only small changes V to V – more efficient to compute V then computing V’ starting from scratch ü Minimize unnecessary recomputation and traversal of DB Goal: generate new SQL queries that perform incremental detection ü modify the SQL detection queries by leveraging DB and V ü design and maintain auxiliary structures (indexing, mark) 64
Logging violations t 1: t 2: t 3: t 4: cc +1 +1 area 908 212 310 phone addr 111 -1111 Elm Str. 222 -2222 Pine Str. 333 -3333 Oak Str. 444 -4444 Main Str. CFD: (area state, T) city MH MH NYC LA zip 07974 01202 90291 state NJ NY NJ CA BC 0 0 1 0 BV 1 1 0 0 area state _ _ 212 NY Use one pair of columns, for each CFD ü Attribute BC records whether tuple t violates query Qc of the CFD ü Attribute BV records whether tuple t violates query Qv of the CFD Initialization: update R t set t[BC] = 1 where t in (QC) update R t set t[BV] = 1 where t in (QV) 65
Handling deletions t 1: t 2: t 3: t 4: cc +1 +1 area 908 212 310 phone 111 -1111 222 -2222 333 -3333 444 -4444 CFD: (area state, T) addr Elm Str. Pine Str. Oak Str. Main Str. area _ 212 state _ NY city MH MH NYC LA zip 07974 01202 90291 state NY NJ NJ CA BC 0 0 1 0 BV 1 1 0 0 How about batch deletions? Let tdel be the tuple we want to delete from R Step 1: delete from R t where t = tdel Step 2: update R t set t[BV] = 0 where t[BV] = 1 AND t[area] = tdel[area] AND 1 = (select count(distinct state) from R t’ where t’[area] = tdel[area]) 66
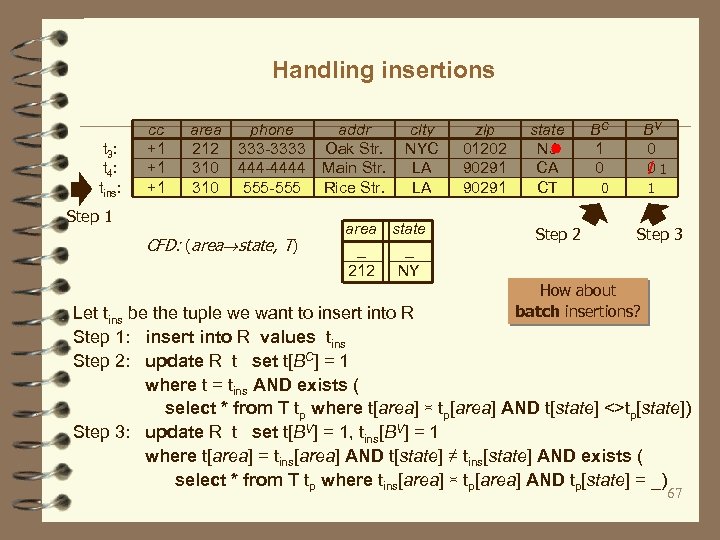
Handling insertions t 3: t 4: tins: cc +1 +1 +1 area 212 310 phone 333 -3333 444 -4444 555 -555 Step 1 CFD: (area state, T) addr Oak Str. Main Str. Rice Str. city NYC LA LA area state _ _ 212 NY zip 01202 90291 state NJ CA CT Step 2 BC 1 0 BV 0 /1 0 0 1 Step 3 How about batch insertions? Let tins be the tuple we want to insert into R Step 1: insert into R values tins Step 2: update R t set t[BC] = 1 where t = tins AND exists ( select * from T tp where t[area] ≍ tp[area] AND t[state] <>tp[state]) Step 3: update R t set t[BV] = 1, tins[BV] = 1 where t[area] = tins[area] AND t[state] ≠ tins[state] AND exists ( select * from T tp where tins[area] ≍ tp[area] AND tp[state] = _) 67
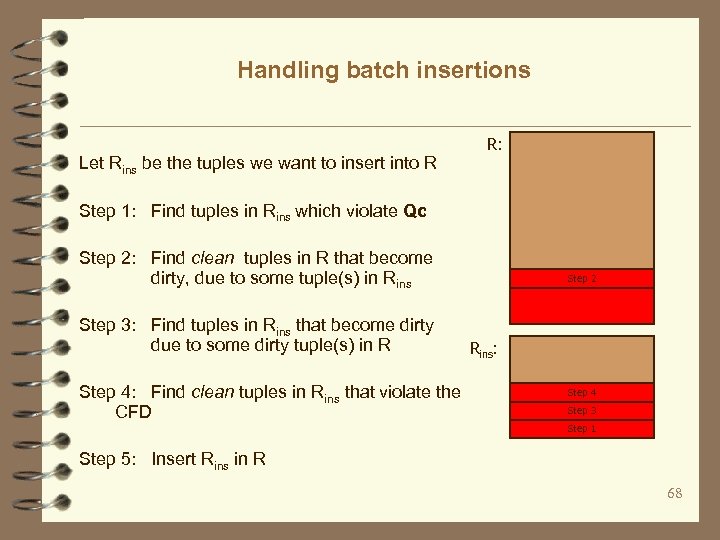
Handling batch insertions Let Rins be the tuples we want to insert into R R: Step 1: Find tuples in Rins which violate Qc Step 2: Find clean tuples in R that become dirty, due to some tuple(s) in Rins Step 3: Find tuples in Rins that become dirty due to some dirty tuple(s) in R Step 4: Find clean tuples in Rins that violate the CFD Step 2 Rins: Step 4 Step 3 Step 1 Step 5: Insert Rins in R 68
The source code Let Rins be the tuples we want to insert into R Step 1: update Rins tins set tins[BC] = 1 where tins in (QC) Step 2: update R t set t[BV] = 1 where t[BC] = 0 AND t[BV] = 0 AND exists (select * from T where t[area] ≍ tp[area] AND tp[state] = _) AND exists (select * from Rins tins where tins[area] = t[area] AND tins[state] ≠ t[state]) Step 3: update Rins tins set tins[BV] = 1 where exists (select * from R t where tins[area] = t[area] AND t[BV] = 1) Step 4: update Rins tins set tins[BV] = 1 where tins[BC] = 0 AND tins[BV] = 0 AND tins[area] IN (select area from Rins t’ins, Tp tp where t’ins[BC] = 0 AND t’ins[BV] = 0 AND t’ins[area] ≍ tp[area] AND tp[state] = _ group by area having count(distinct state) > 1) Step 5: insert into R values (select * from Rins) 69
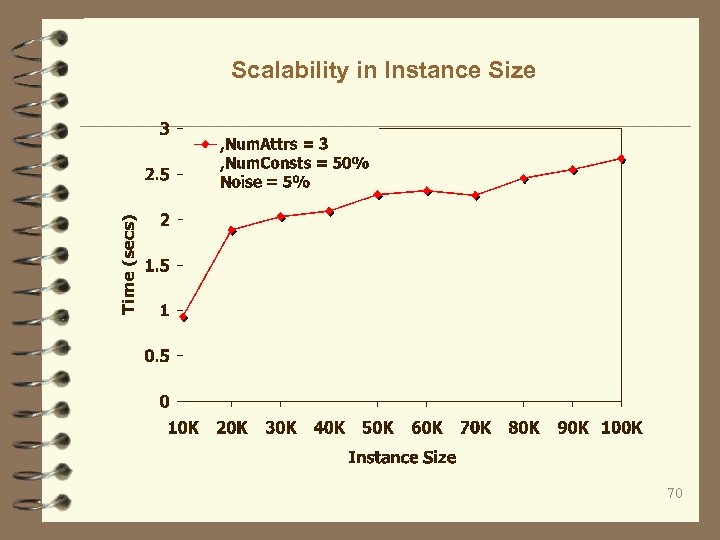
Scalability in Instance Size 70
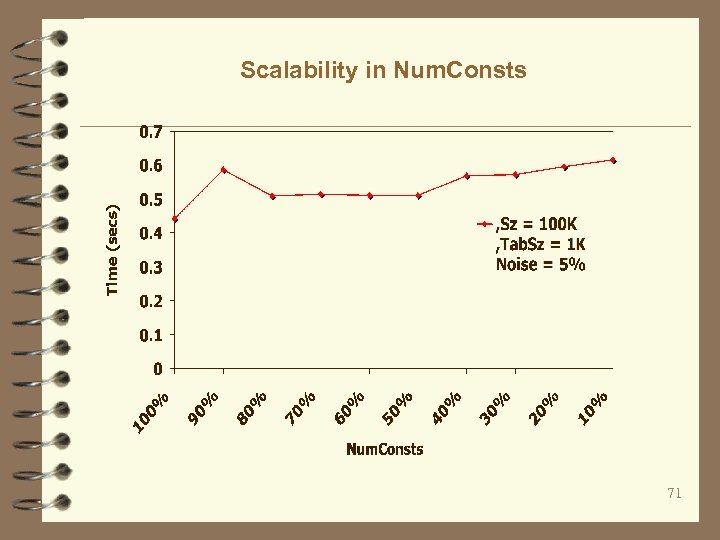
Scalability in Num. Consts 71
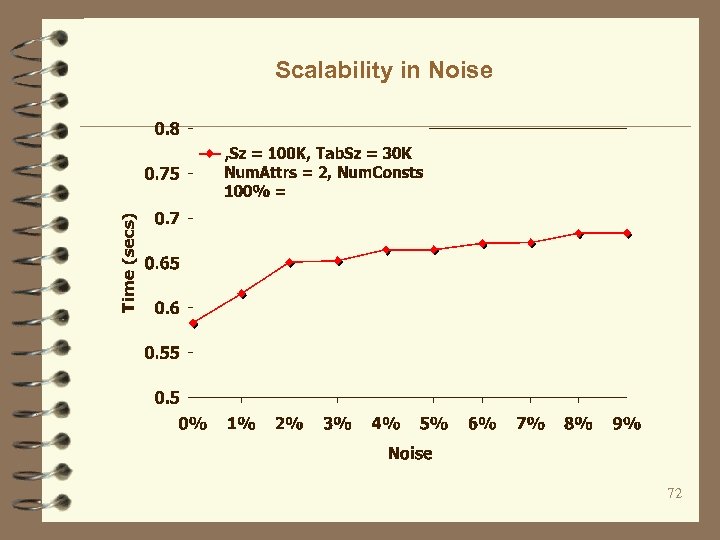
Scalability in Noise 72
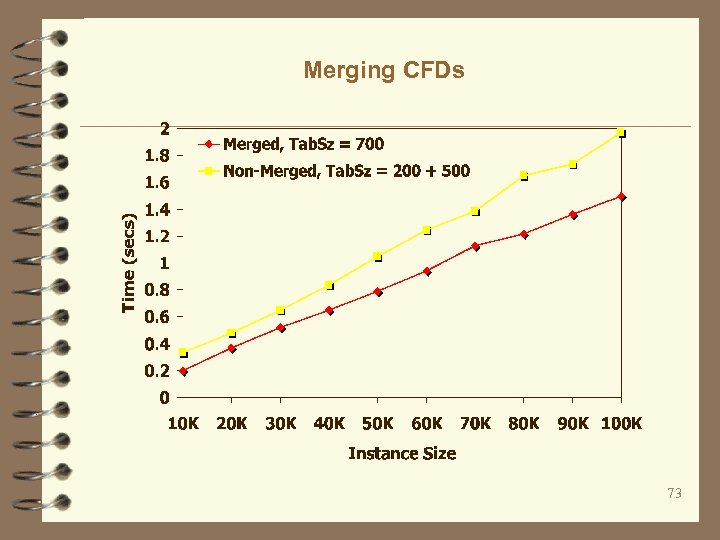
Merging CFDs 73
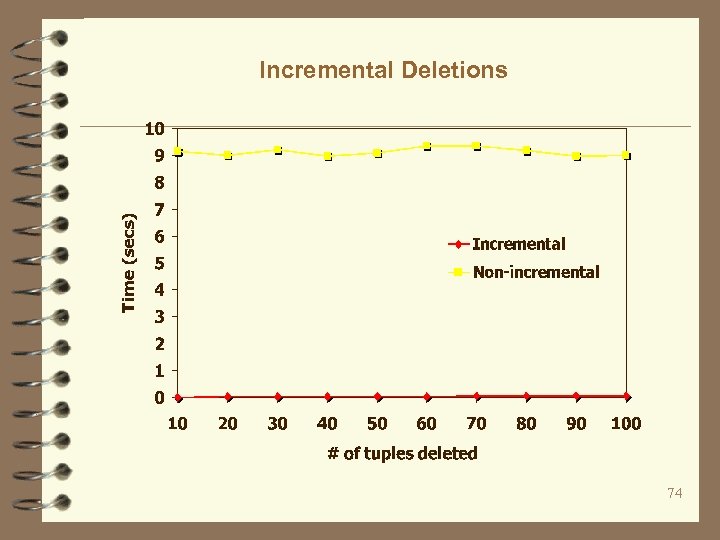
Incremental Deletions 74
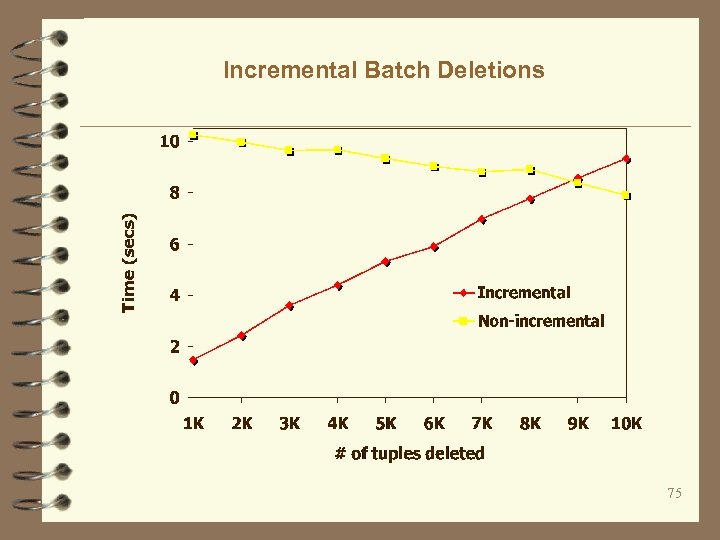
Incremental Batch Deletions 75
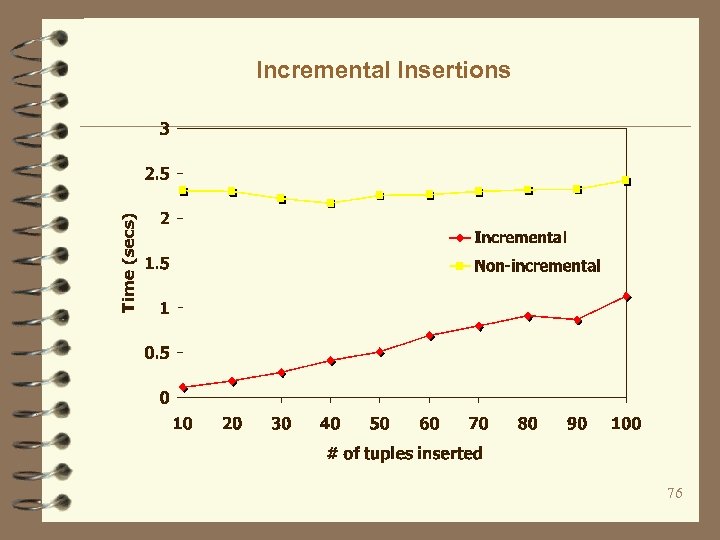
Incremental Insertions 76
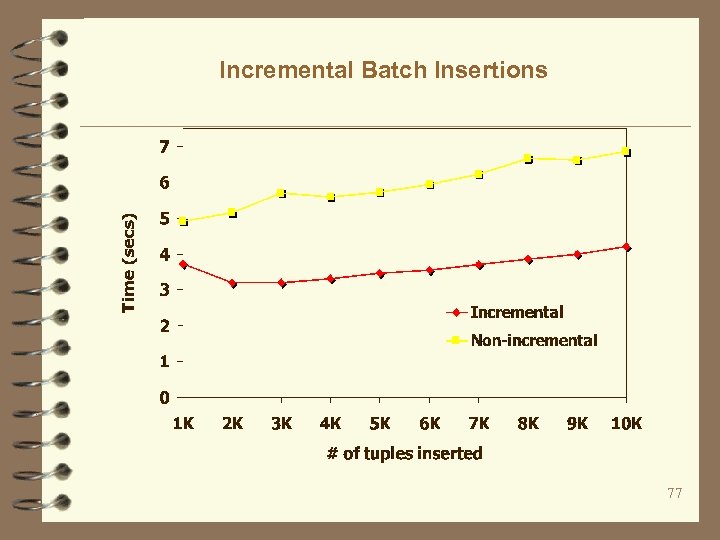
Incremental Batch Insertions 77
Checking the satisfiability of CFDs Input: a set of CFDs MAXSC: find a maximum subset of that is consistent Complexity: the MAXSC problem for CFDs is NP-complete Theorem: there is an -approximation algorithm for MAXSC ü there exist constant such that for the subset m found by the algorithm has a bound: card( m) > card(OPT( )) Proof idea: approximation factor preserving reduction to MAXGSAT Open questions: effective heuristic algorithms ü for checking the satisfiability of CFDs + CINDs (undecidable) ü for determining implication of CFDs, CINDs, and CFDs + CINDs ü for finding minimum cover of CFDs, CINDs, and CFDs + CINDs 78
Automated methods for finding a repair Input: a relational database DB, and a set of CFDs Output: a repair DB’ of DB such that cost(DB’, DB) is minimal ü repair: DB’ satisfies ü “good”: cost(DB’, DB) – DB’ is “close” to the original data in DB – Minimizing changes to “accurate” attributes Complexity: Finding an optimal repair is ü NP-complete (data complexity) for traditional FDs, for a fixed set of FDs (or INDs) and fixed schema ü PSPACE-complete for CFDs + CINDs (combined complexity) Open questions: effective heuristic for repairing databases based on CFDs, CINDs, and CFDs + CINDs 79
Incremental repair Input: a clean database DB, changes DB to DB, and a set of CFDs Output: a repair DB’ of DB + DB Complexity. The local data cleaning problem is NP-hard, even if DB consists of a single tuple. Open questions: find effective heuristic algorithms for incrementally repairing databases based on ü CFDs ü CINDs ü CFDs + CINDs 80
Discovering CFDs and CINDs Input: Sample databases of a schema R Output: CFDs and CINDs that hold on all (or most) database instances of R Difficulty. A naïve approach may find non-representative CFDs and CINDs as large as the sample data Open questions: find effective method for discovering ü CFDs ü CINDs ü CFDs + CINDs 81
Summary ü Conditional functional dependencies – for data cleaning rather than schema design – complexity bounds of satisfiability and implication analyses – a sound and complete inference system ü Conditional inclusion dependencies – for data cleaning and schema matching in practice – complexity bounds of satisfiability and implication analyses – a sound and complete inference system ü Complexity bounds for CFDs and CINDs taken together ü SQL techniques for automatic detection of CFD violations – a pair of SQL queries for validating multiple CFDs – incremental techniques for validating CFDs A practical method for data cleaning and schema matching 82
References ü Conditional Functional Dependencies for Data Cleaning The 23 rd International Conference on Database Engineering (ICDE), 2007. Philip Bohannon, Wenfei Fan, Floris Geerts, Xibei Jia, Anastasios Kementsietsidis ü Extending Dependencies with Conditions Loreto Bravo, Wenfei Fan, Shuai Ma ü Improving Data Quality: Consistency and Accuracy Gao Cong, Wenfei Fan, Floris Geerts, Xibei Jia, Shuai Ma ü Conditional Functional Dependencies for Capturing Data Inconsistencies Wenfei Fan, Floris Geerts, Xibei Jia, Anastasios Kementsietsidis 83
Скачать презентацию Conditional Dependencies Wenfei Fan University of Edinburgh and
046fa2dd2ce19a6405587f0c9c181c15.ppt