Concurrent Lines Medians and Triangles Angle Relationships in

Concurrent Lines, Medians, and Triangles Angle Relationships in Altitudes Warm Up 1. Draw a triangle and construct the bisector of one angle. 2. JK is perpendicular to ML at its midpoint K. List the congruent segments. 1

Concurrent Lines, Medians, and Triangles Angle Relationships in Altitudes Since a triangle has three sides, it has three perpendicular bisectors. When you construct the perpendicular bisectors, you find that they have an interesting property. 2

Concurrent Lines, Medians, and Triangles Angle Relationships in Altitudes When three or more lines intersect at one point, the lines are said to be concurrent. The point of concurrency is the point where they intersect. The three perpendicular bisectors of a triangle are concurrent. This point of concurrency is the circumcenter of the triangle. 3

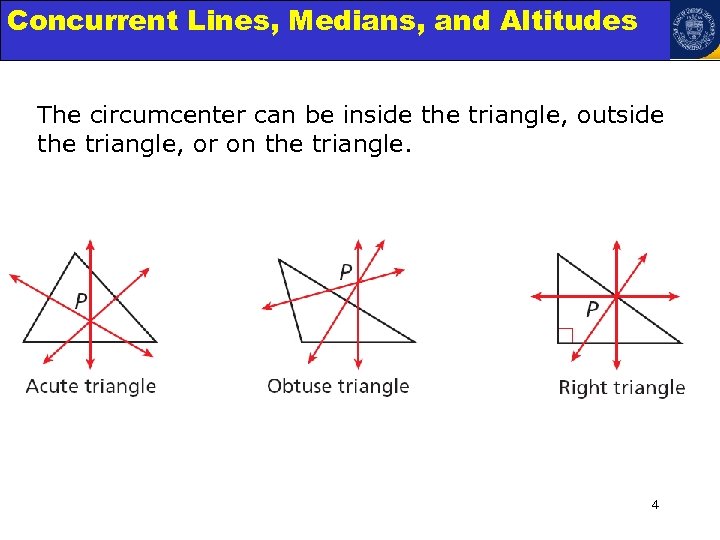Concurrent Lines, Medians, and Triangles Angle Relationships in Altitudes The circumcenter can be inside the triangle, outside the triangle, or on the triangle. 4

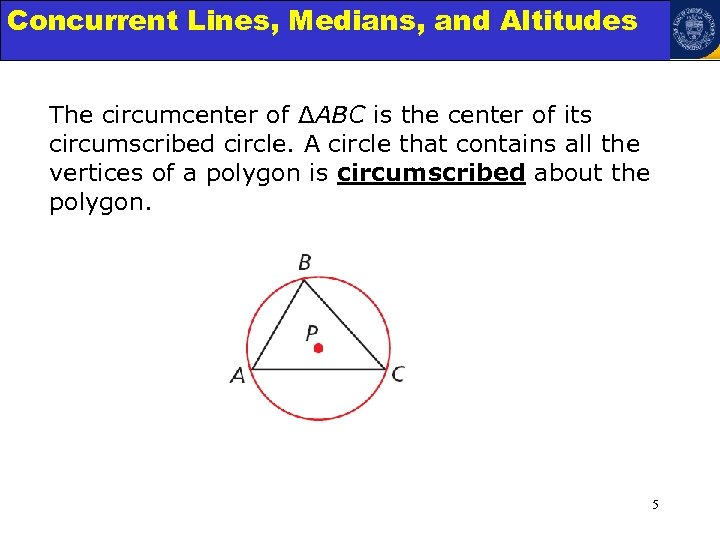Concurrent Lines, Medians, and Triangles Angle Relationships in Altitudes The circumcenter of ΔABC is the center of its circumscribed circle. A circle that contains all the vertices of a polygon is circumscribed about the polygon. 5

Concurrent Lines, Medians, and Triangles Angle Relationships in Altitudes Example 1: Using Properties of Perpendicular Bisectors DG, EG, and FG are the perpendicular bisectors of ∆ABC. Find GC. 6

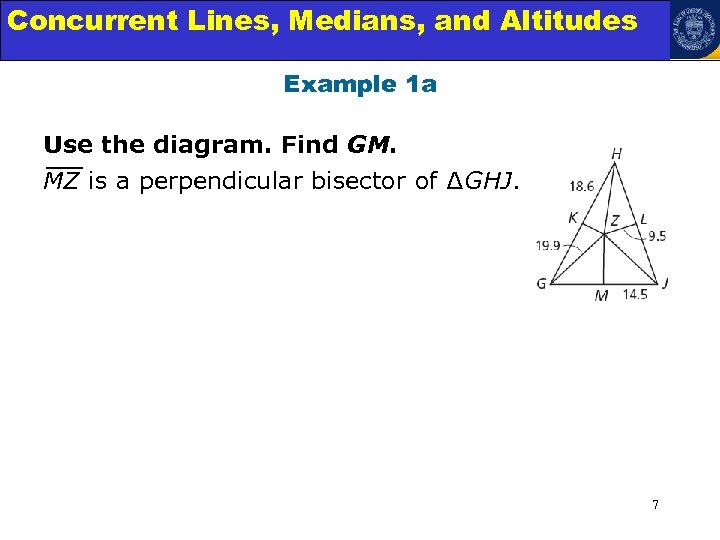Concurrent Lines, Medians, and Triangles Angle Relationships in Altitudes Example 1 a Use the diagram. Find GM. MZ is a perpendicular bisector of ∆GHJ. 7

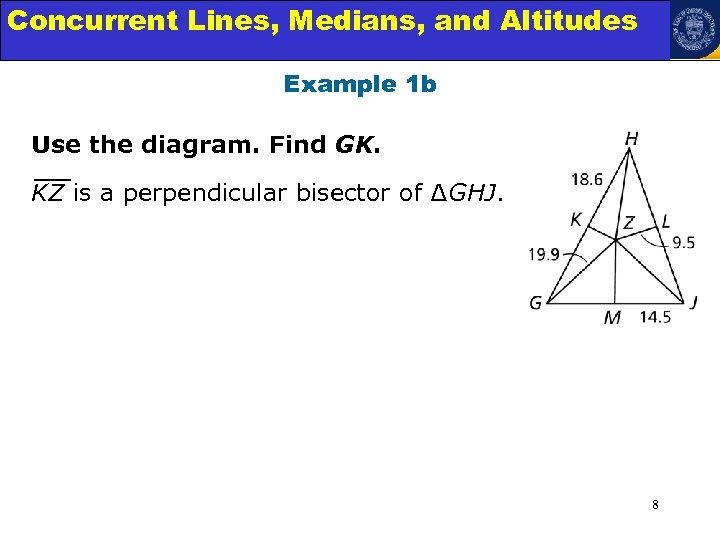Concurrent Lines, Medians, and Triangles Angle Relationships in Altitudes Example 1 b Use the diagram. Find GK. KZ is a perpendicular bisector of ∆GHJ. 8

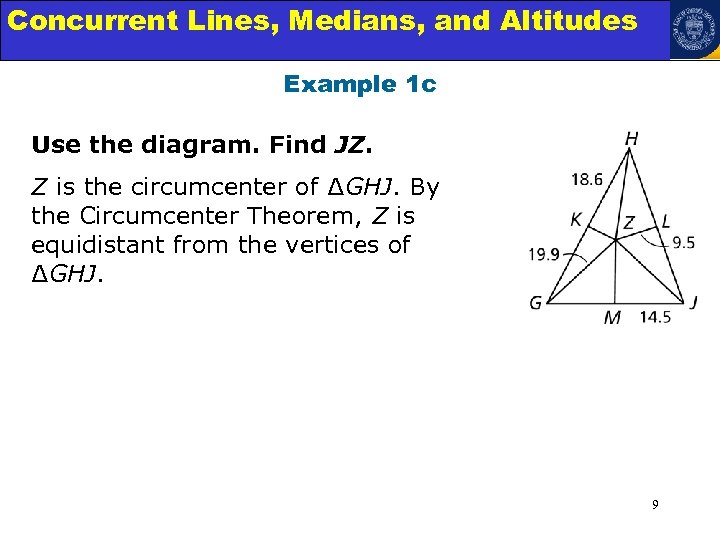Concurrent Lines, Medians, and Triangles Angle Relationships in Altitudes Example 1 c Use the diagram. Find JZ. Z is the circumcenter of ∆GHJ. By the Circumcenter Theorem, Z is equidistant from the vertices of ∆GHJ. 9

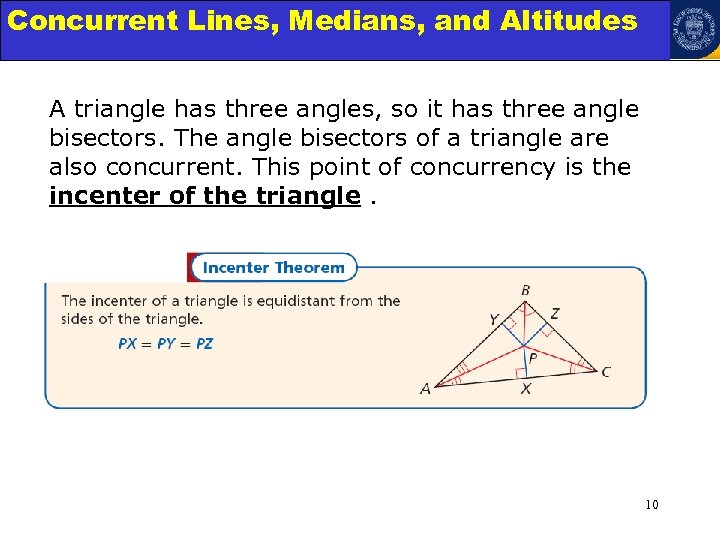Concurrent Lines, Medians, and Triangles Angle Relationships in Altitudes A triangle has three angles, so it has three angle bisectors. The angle bisectors of a triangle are also concurrent. This point of concurrency is the incenter of the triangle. 10

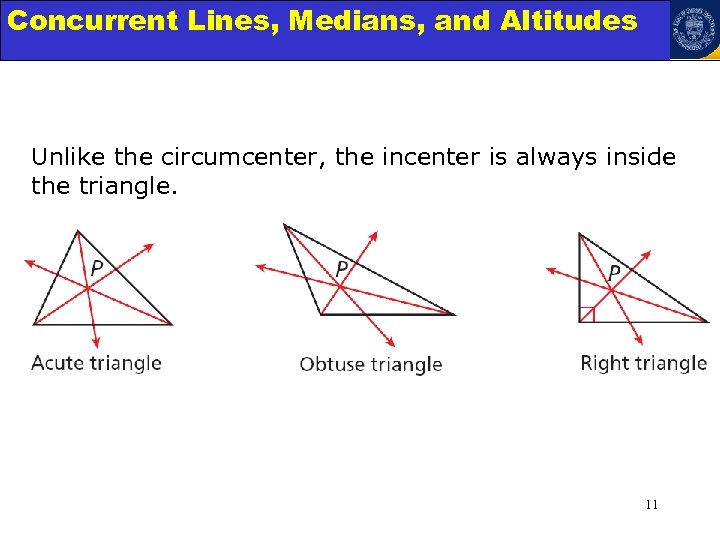Concurrent Lines, Medians, and Triangles Angle Relationships in Altitudes Unlike the circumcenter, the incenter is always inside the triangle. 11

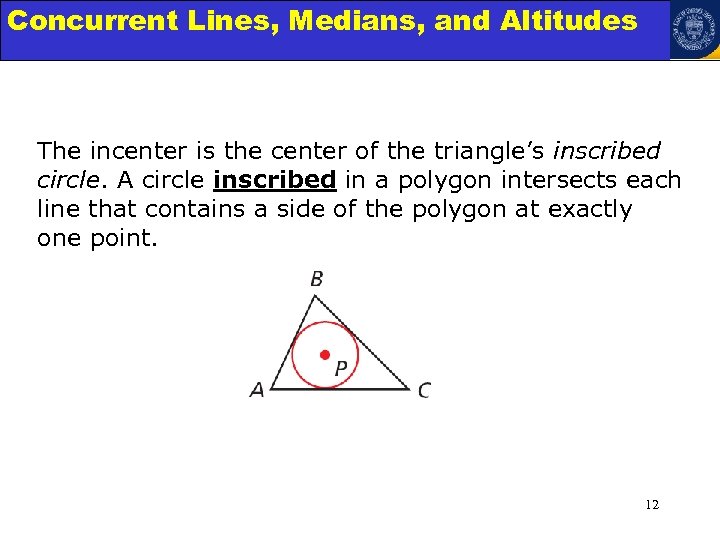Concurrent Lines, Medians, and Triangles Angle Relationships in Altitudes The incenter is the center of the triangle’s inscribed circle. A circle inscribed in a polygon intersects each line that contains a side of the polygon at exactly one point. 12

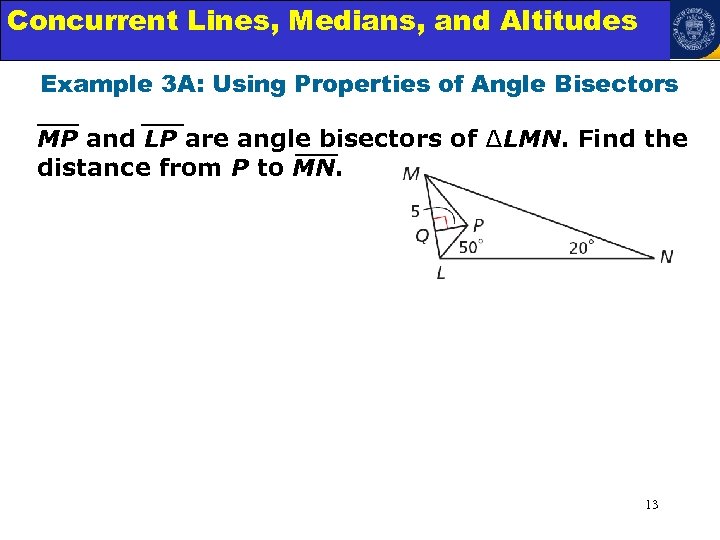Concurrent Lines, Medians, and Triangles Angle Relationships in Altitudes Example 3 A: Using Properties of Angle Bisectors MP and LP are angle bisectors of ∆LMN. Find the distance from P to MN. 13

Concurrent Lines, Medians, and Triangles Angle Relationships in Altitudes Example 3 B: Using Properties of Angle Bisectors MP and LP are angle bisectors of ∆LMN. Find m PMN. 14

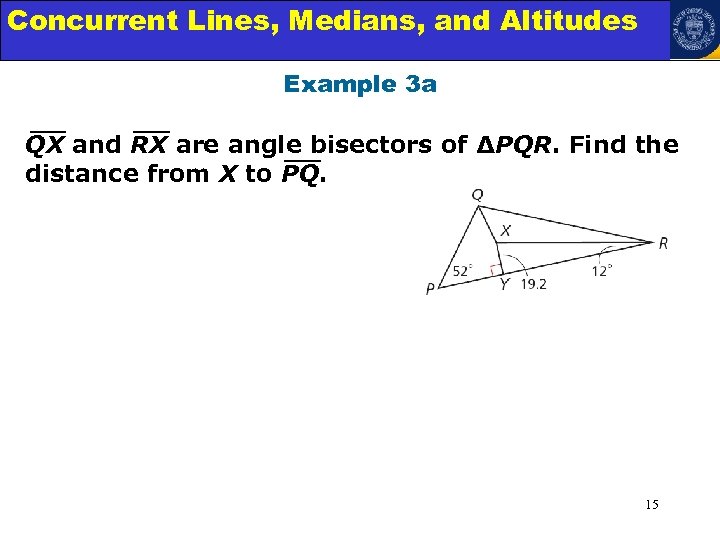Concurrent Lines, Medians, and Triangles Angle Relationships in Altitudes Example 3 a QX and RX are angle bisectors of ΔPQR. Find the distance from X to PQ. 15

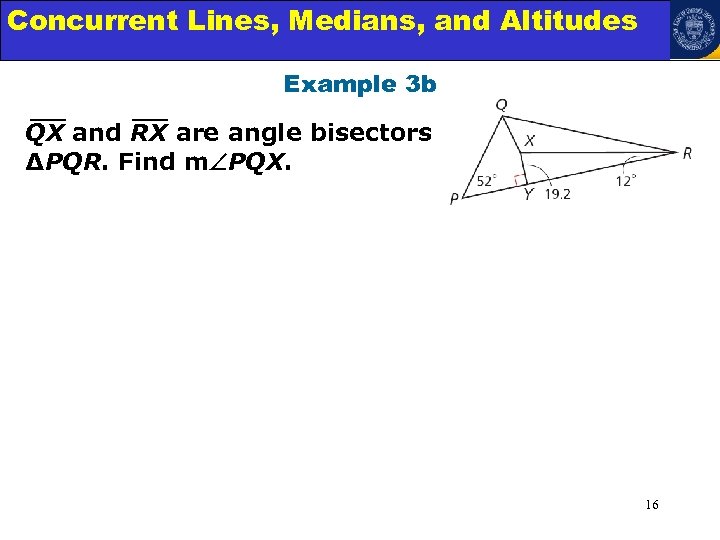Concurrent Lines, Medians, and Triangles Angle Relationships in Altitudes Example 3 b QX and RX are angle bisectors of ∆PQR. Find m PQX. 16

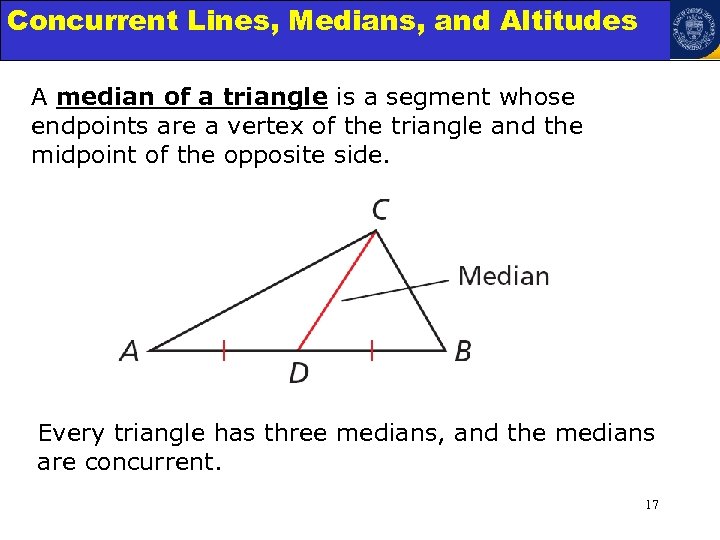Concurrent Lines, Medians, and Triangles Angle Relationships in Altitudes A median of a triangle is a segment whose endpoints are a vertex of the triangle and the midpoint of the opposite side. Every triangle has three medians, and the medians are concurrent. 17

Concurrent Lines, Medians, and Triangles Angle Relationships in Altitudes The point of concurrency of the medians of a triangle is the centroid of the triangle. The centroid is always inside the triangle. The centroid is also called the center of gravity because it is the point where a triangular region will balance. 18

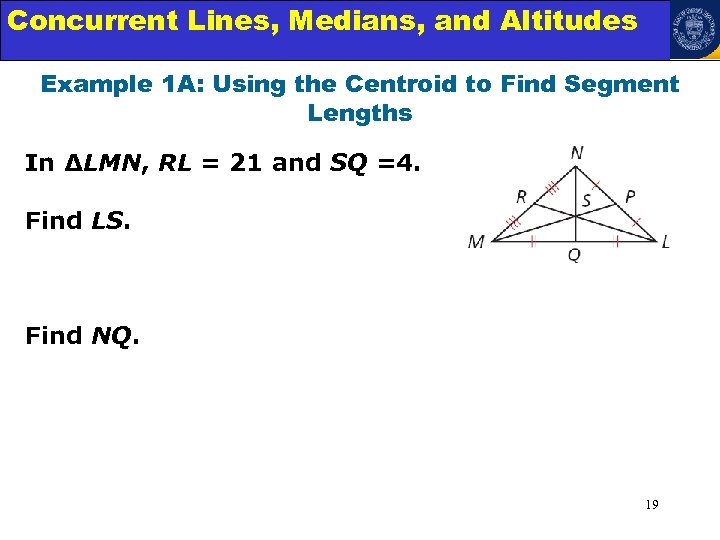Concurrent Lines, Medians, and Triangles Angle Relationships in Altitudes Example 1 A: Using the Centroid to Find Segment Lengths In ∆LMN, RL = 21 and SQ =4. Find LS. Find NQ. 19

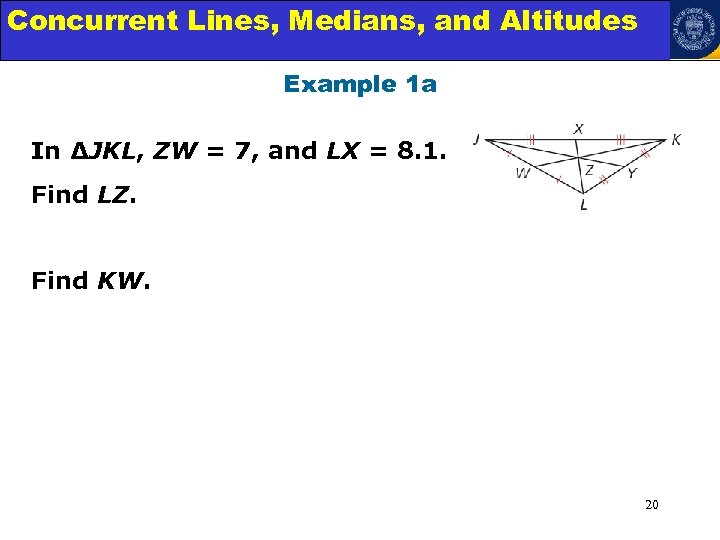Concurrent Lines, Medians, and Triangles Angle Relationships in Altitudes Example 1 a In ∆JKL, ZW = 7, and LX = 8. 1. Find LZ. Find KW. 20

Concurrent Lines, Medians, and Triangles Angle Relationships in Altitudes An altitude of a triangle is a perpendicular segment from a vertex to the line containing the opposite side. Every triangle has three altitudes. An altitude can be inside, outside, or on the triangle. 21

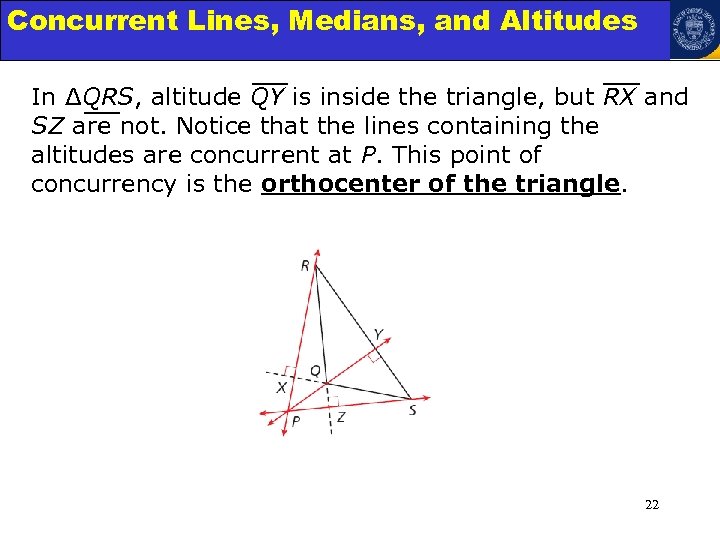Concurrent Lines, Medians, and Triangles Angle Relationships in Altitudes In ΔQRS, altitude QY is inside the triangle, but RX and SZ are not. Notice that the lines containing the altitudes are concurrent at P. This point of concurrency is the orthocenter of the triangle. 22

Concurrent Lines, Medians, and Triangles Angle Relationships in Altitudes Lesson Review: Part I 1. ED, FD, and GD are the perpendicular bisectors of ∆ABC. Find BD. 2. JP, KP, and HP are angle bisectors of ∆HJK. Find the distance from P to HK. 23

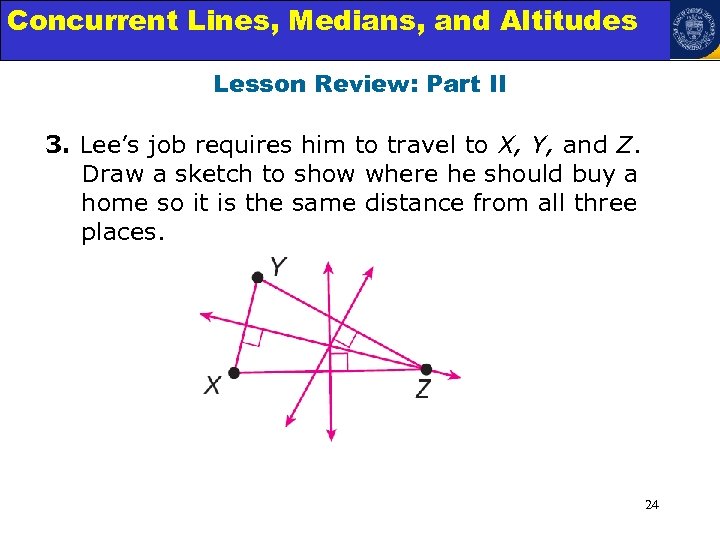Concurrent Lines, Medians, and Triangles Angle Relationships in Altitudes Lesson Review: Part II 3. Lee’s job requires him to travel to X, Y, and Z. Draw a sketch to show where he should buy a home so it is the same distance from all three places. 24