75962974161956802db043a0cbb1bb84.ppt
- Количество слайдов: 11

Computing Reachable Sets via Toolbox of Level Set Methods Michael Vitus (michael. vitus@gmail. com) Jerry Ding (jding@eecs. berkeley. edu) 4/16/2012

Toolbox of Level Set Methods • Ian Mitchell – Professor at the University of British Columbia • http: //www. cs. ubc. ca/~mitchell/ • Toolbox – Matlab – Computes the backwards reachable set – Fixed spacing Cartesian grid – Arbitrary dimension (computationally limited)

Problem Formulation • Dynamics: – System input: – Disturbance input: • Target set: – Unsafe final conditions

Backwards Reachable Set • Solution to a Hamilton-Jacobi PDE: where: • Terminal value HJ PDE – Converted to an initial value PDE by multiplying the H(x, p) by -1

Toolbox Formulation • No automated method • Provide 3 items – Hamiltonian function (multiplied by -1) – An upper bound on the partials function – Final target set

General Comments • Hamiltonian overestimated reachable set underestimated • Partials function – Most difficult – Underestimation numerical instability – Overestimation rounded corners or worst case underestimation of reachable set • Computation – The solver grids the state space – Tractable only up to 6 continuous states • Toolbox – Coding: ~90% is setting up the environment

Useful Dynamical Form • Nonlinear system, linear input • Input constraints are hyperrectangles • Analytical optimal inputs: • Partials upper bound:
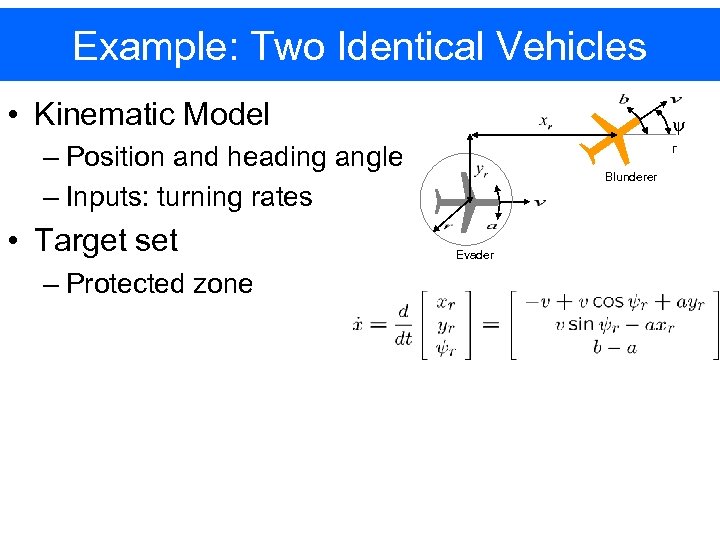
Example: Two Identical Vehicles • Kinematic Model y – Position and heading angle – Inputs: turning rates • Target set – Protected zone r Blunderer Evader

Example • Optimal Hamiltonian: • Partials:
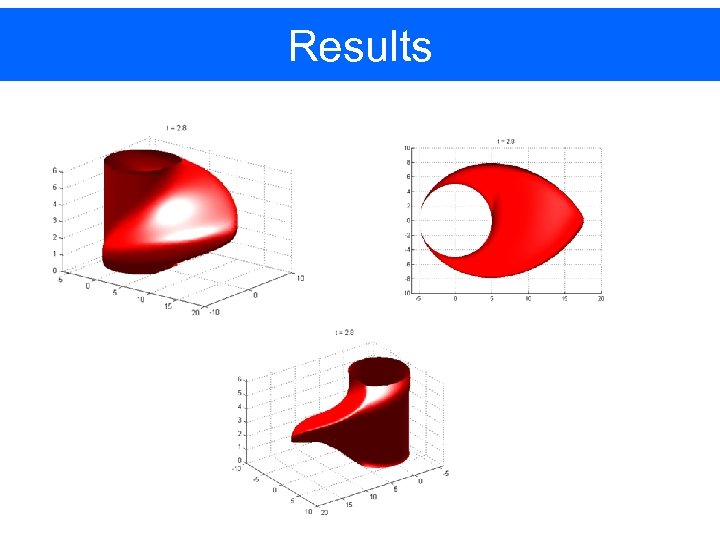
Results

Toolbox • Plotting utilities – KernelHelperVisualization – visualize. Level. Set. m – spin. Animation. m • Initial condition helpers – Cylinders, hyperrectangles • Advice: Start small… • Walk through example
75962974161956802db043a0cbb1bb84.ppt