Computing handles and tunnels in 3 D models

Computing handles and tunnels in 3 D models Tamal K. Dey Joint work: Kuiyu Li, Jian Sun, D. Cohen-Steiner

Projects in Jyamiti group • Surface reconstrucion (Cocone) • Delaunay meshing (Del. PSC) • Shape feature processing (Segmatch, Cskel)

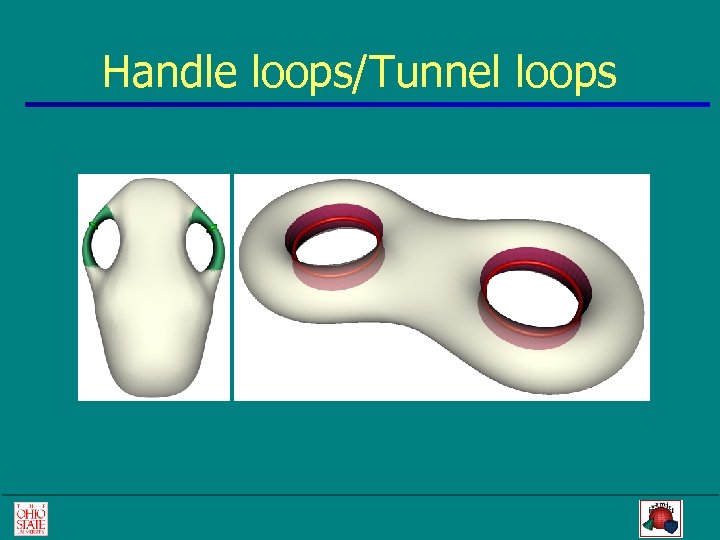Handle loops/Tunnel loops

Handle loops/Tunnel loops

Topological Simplification

Use of Handles and Tunnels • Topological simplification / feature recognition / parameterization • El-Sana and Varshney[1997] use α-hulls to search for tunnels. • Guskov and Wood[2001] propose a surface growing strategy to remove small handles. • Nooruddin and Turk[2003] use morphological operations to remove small handles. • Wood, Hoppe, Desbrun, and Schroder[2004] use Reeb graph to remove handles. • Shattuck and Leahy[2001] use Reeb graph to compute handles. • From WUSTL Model/surface editing (Zhou, Ju, and Hu[2007] use medial axis to detect loops) and work by Grimm et al.

Nontrivial loops as first attempt? • • Nontrivial loops can neither be handle nor tunnel. Handle and tunnel loops have to be nonseparating.

Related work for loops on surface • Loops on a surface • Compute polygon schemas [Vegter-Yap 90][Dey-Schipper 95] • Linear time algorithm • Compute optimal systems of loops [VL 05][EW 06] • Verdiere and Lazarus gave an algorithm for computing a system of loops which is shortest among the homotopy class of a given one. • Erickson and Whittlesey gave a greedy algorithm to compute the shortest system of loops among all systems of loops. • Compute optimal cut graph [EH 04] • Computing a shortest cut graph is NP-hard.

A better idea • Intuitively, a loop on a connected, closed, surface M in R 3 is: • handleif it spans a disk (surface) in the bounded space bordered by M. • tunnelif it spans a disk (surface) in the unbounded space bordered by M.

Cycle, Boundary and Homology

Cycle, Boundary and Homology

Handle and tunnel loops definitions [Dey-Li-Sun 07] • Let M be a connected, closed, surface in R 3. M separates R 3 into inside I and outside O. Both I and O have M as boundary. • Handle A loop on M whose : homology class is trivial in H 1(I) and non-trivial in H 1(O). • Tunnel A loop on M whose : homology class is trivial in H 1(O) and non-trivial in H 1(I). –

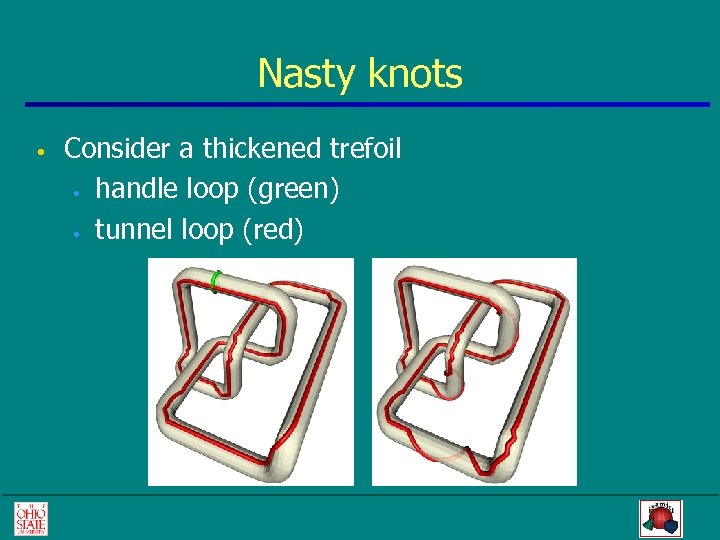Nasty knots • Consider a thickened trefoil • handle loop (green) • tunnel loop (red)

Handle and tunnel loops – existence • Theorem (Dey, Li, Sun[2007]) • For any connected closed surface M of genus g in R 3, there exist g handle loops {hi}i=1…g forming a basis for H 1(O) and g tunnel loops {ti}i=1. . . g forming a basis for H 1(I). • Furthermore, {hi}i=1. . . g and {ti}i=1. . . g form a basis for H 1(M).

First algorithm for GR models [Dey-Li-Sun 07] • Graph retractability assumption : A surface is graph retractable if both I and O deformation retract to a graph, denoted I and O, respectively.

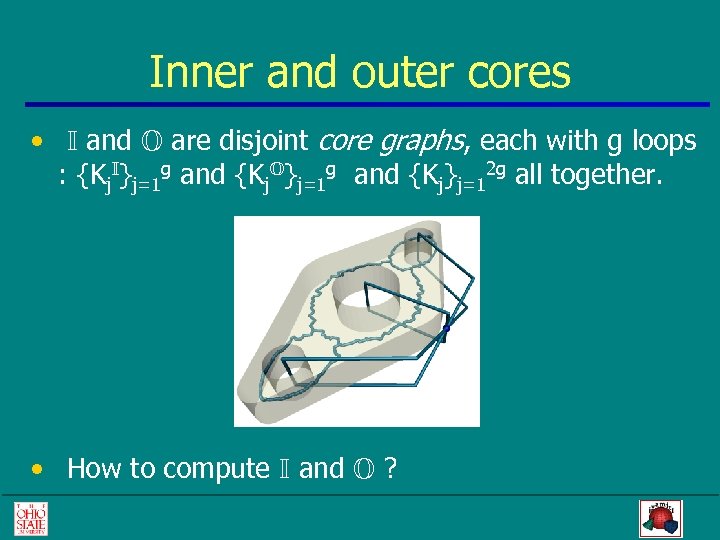Inner and outer cores • I and O are disjoint core graphs, each with g loops : {Kj. I}j=1 g and {Kj. O}j=1 g and {Kj}j=12 g all together. • How to compute I and O ?

Linking number • J and K are two disjoint loops in R 3. • In a regular projection, there are two ways in which J crosses under K. • The linking number, lk(K, J), is the sum of these signed crossings.

Linking number Theorem

Minimally linked basis

Topological algorithm

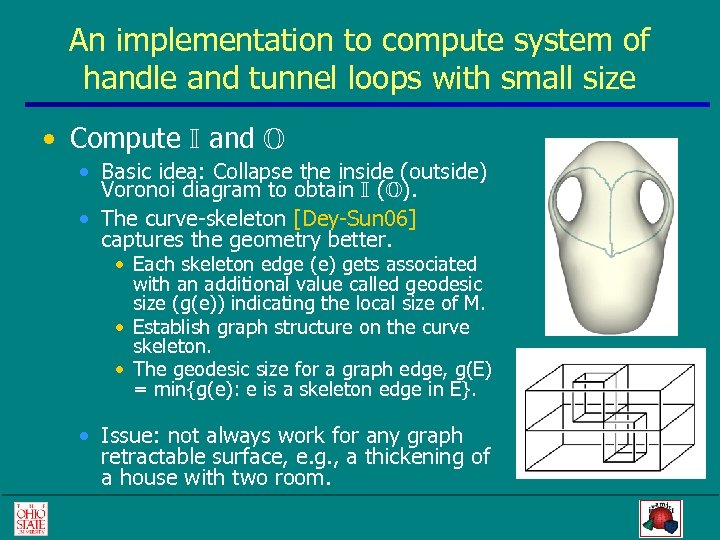An implementation to compute system of handle and tunnel loops with small size • Compute I and O • Basic idea: Collapse the inside (outside) Voronoi diagram to obtain I (O). • The curve-skeleton [Dey-Sun 06] captures the geometry better. • Each skeleton edge (e) gets associated with an additional value called geodesic size (g(e)) indicating the local size of M. • Establish graph structure on the curve skeleton. • The geodesic size for a graph edge, g(E) = min{g(e): e is a skeleton edge in E}. • Issue: not always work for any graph retractable surface, e. g. , a thickening of a house with two room.

Core graphs by curve-skeletons[DS 05]

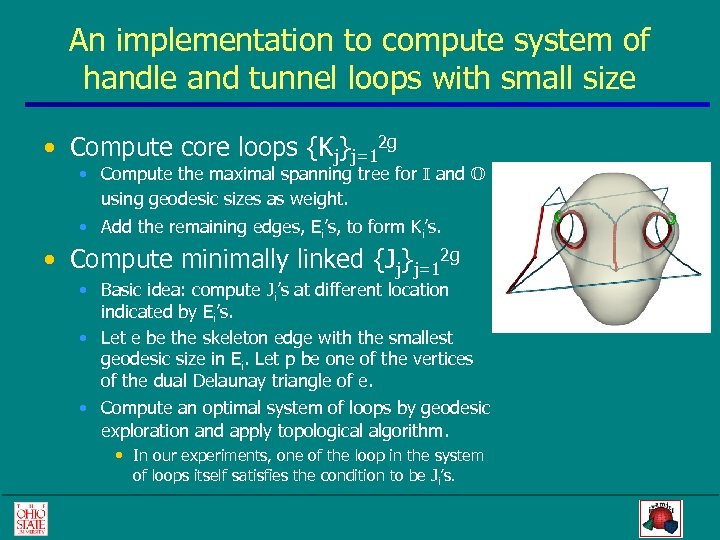An implementation to compute system of handle and tunnel loops with small size • Compute core loops {Kj}j=12 g • Compute the maximal spanning tree for I and O using geodesic sizes as weight. • Add the remaining edges, Ei’s, to form Ki’s. • Compute minimally linked {Jj}j=12 g • Basic idea: compute Ji’s at different location indicated by Ei’s. • Let e be the skeleton edge with the smallest geodesic size in Ei. Let p be one of the vertices of the dual Delaunay triangle of e. • Compute an optimal system of loops by geodesic exploration and apply topological algorithm. • In our experiments, one of the loop in the system of loops itself satisfies the condition to be Ji’s.

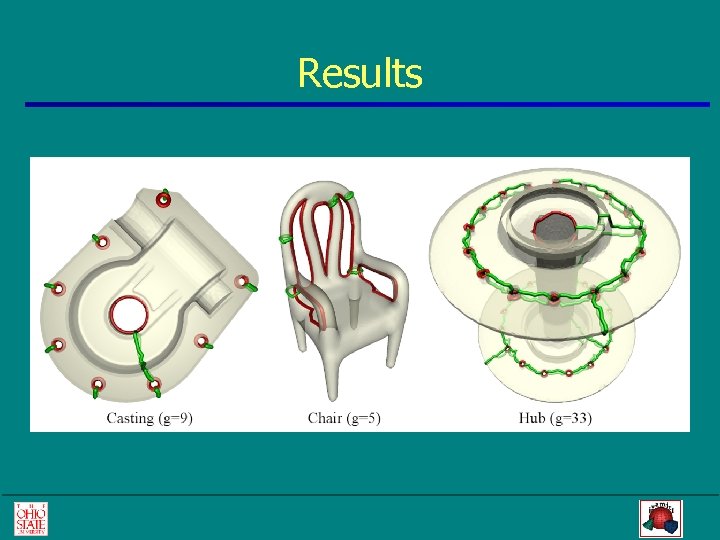Results

A Persistence based algorithm [Dey-Li-Sun-Cohen-Steiner 08] • A fast algorithm based on persistent homology introduced by Edelsbrunner, Letscher, Zomorodian[2002]. • The algorithm does not require any extra structure such as medial axis, curve skeleton, or Reeb graphs. • It works on a larger class of models. Both surface mesh and isosurface with volume grids can be input.

Filtration in persistent homology

Positive and Negative simplices

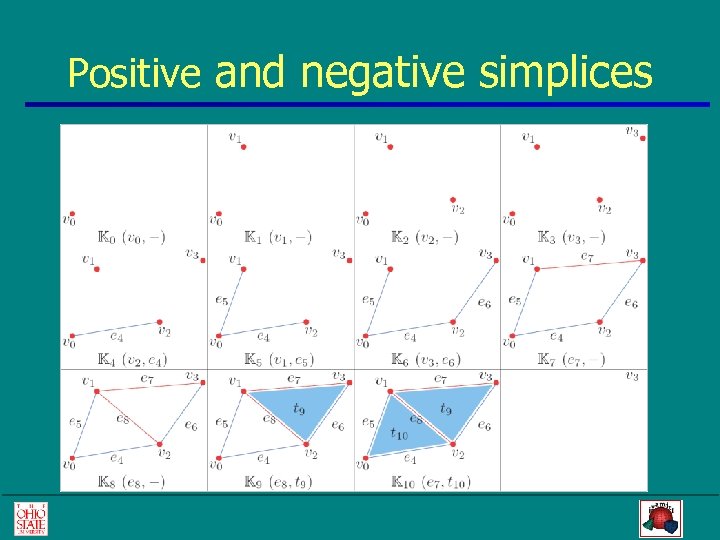Positive and negative simplices

Computing handle and tunnel loops • Topological algorithm • Two refinements for improving loop quality. • Assume M, I, and O denote the simplicial complexes of surface, inside, and outside respectively; g is the genus of M.

Topological algorithm • 3 Steps: • 1) Simplices of M are added to the filtration, generating 2 g unpaired positive edges; • 2) Simplices of I are added, g previously unpaired edges get paired, each pair corresponds to a handle loop; • 3) Simplices of O are added, the rest of g unpaired edges get paired, each pair corresponds to a tunnel loop.

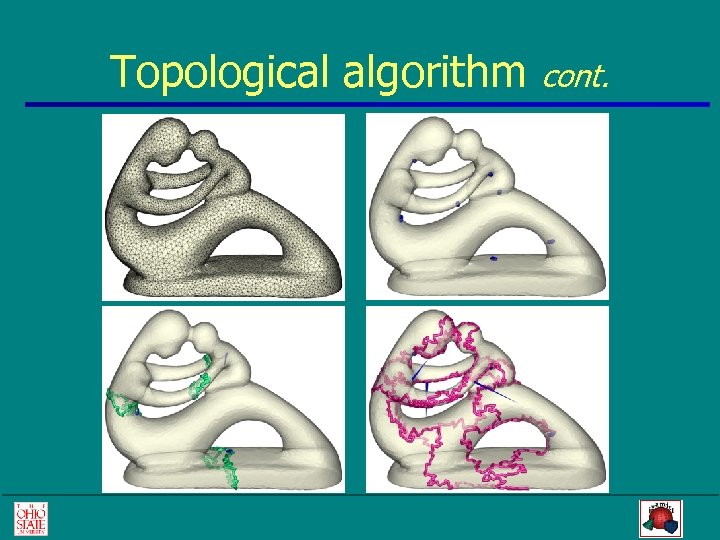Topological algorithm cont.

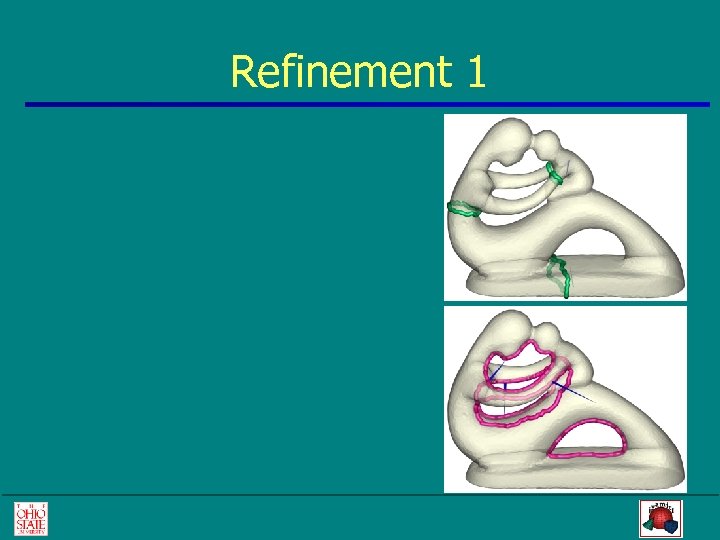Refinement 1

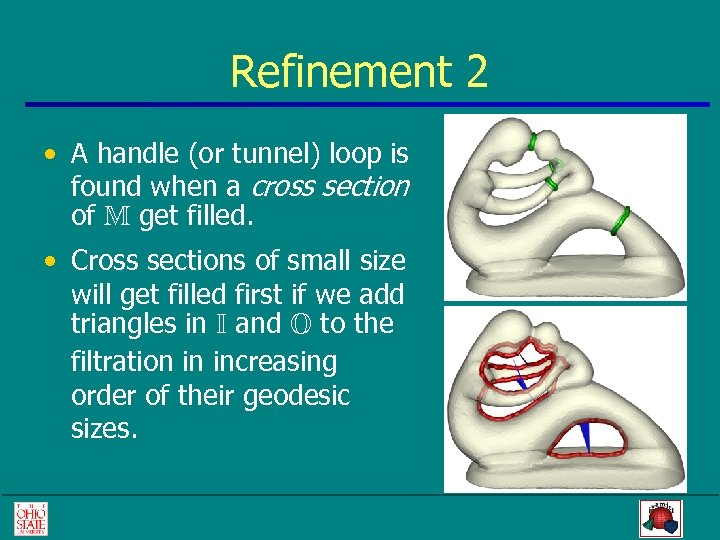Refinement 2 • A handle (or tunnel) loop is found when a cross section of M get filled. • Cross sections of small size will get filled first if we add triangles in I and O to the filtration in increasing order of their geodesic sizes.

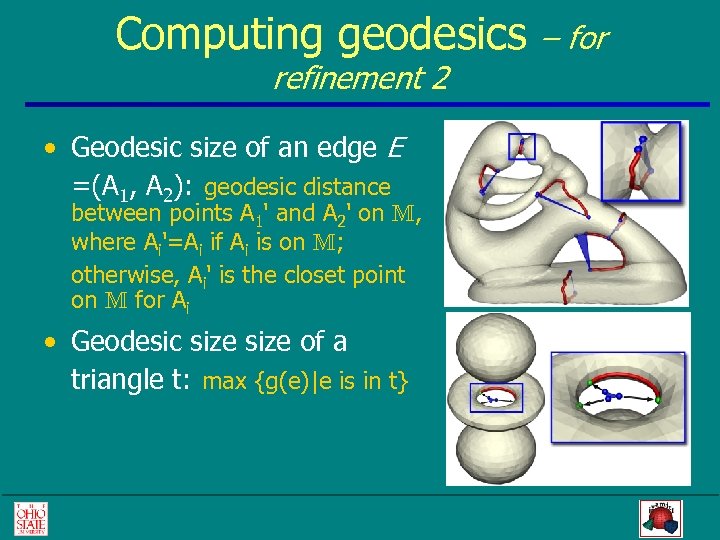Computing geodesics refinement 2 • Geodesic size of an edge E =(A 1, A 2): geodesic distance between points A 1' and A 2' on M, where Ai'=Ai if Ai is on M; otherwise, Ai' is the closet point on M for Ai • Geodesic size of a triangle t: max {g(e)|e is in t} – for

Entire algorithm

Entire algorithm

Gearbox (genus 78)

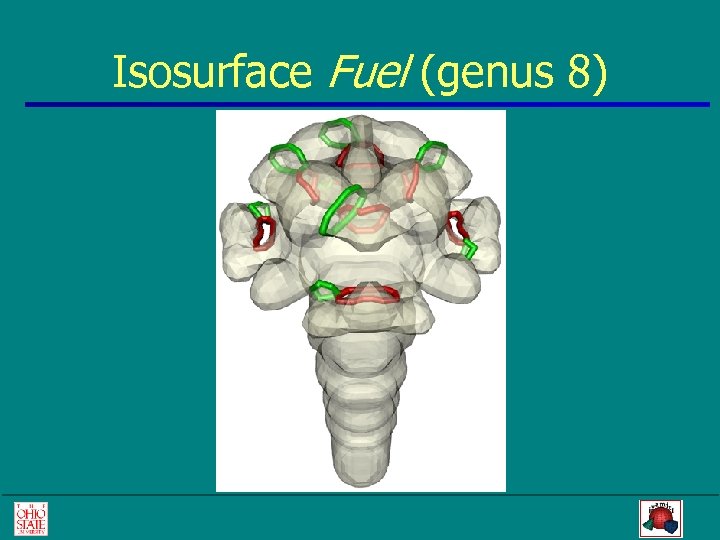Isosurface Fuel (genus 8)

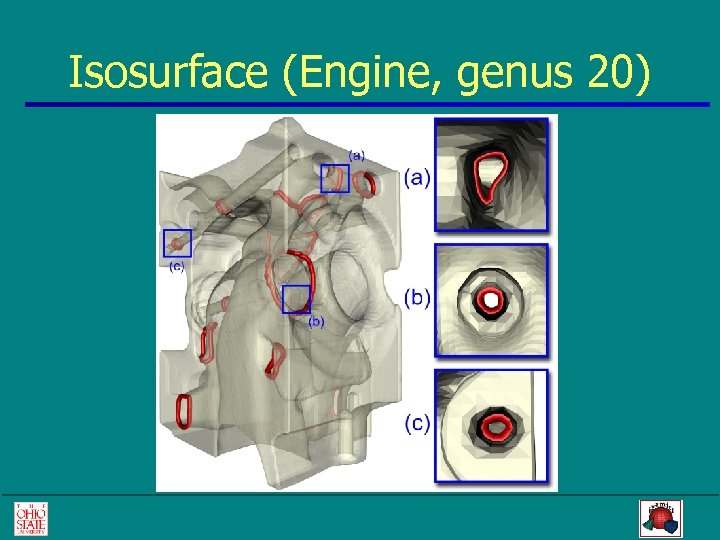Isosurface (Engine, genus 20)

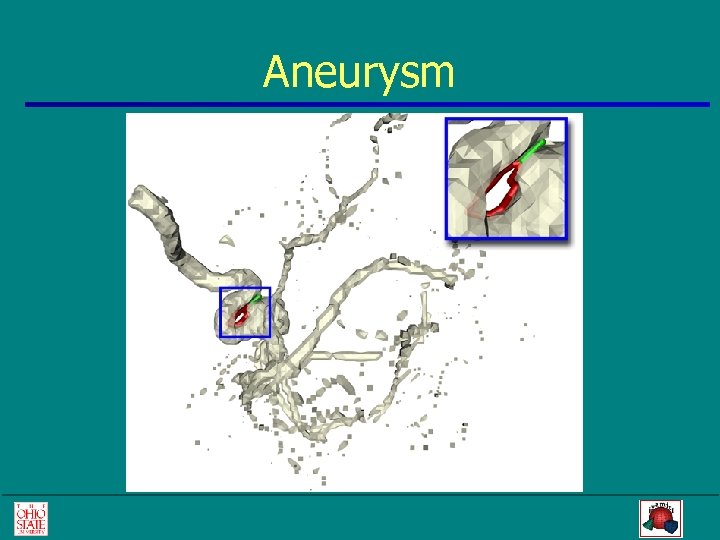Aneurysm

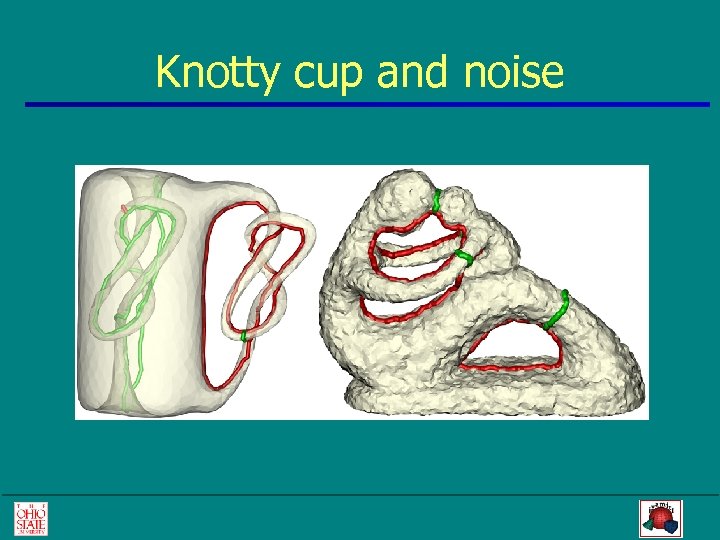Knotty cup and noise

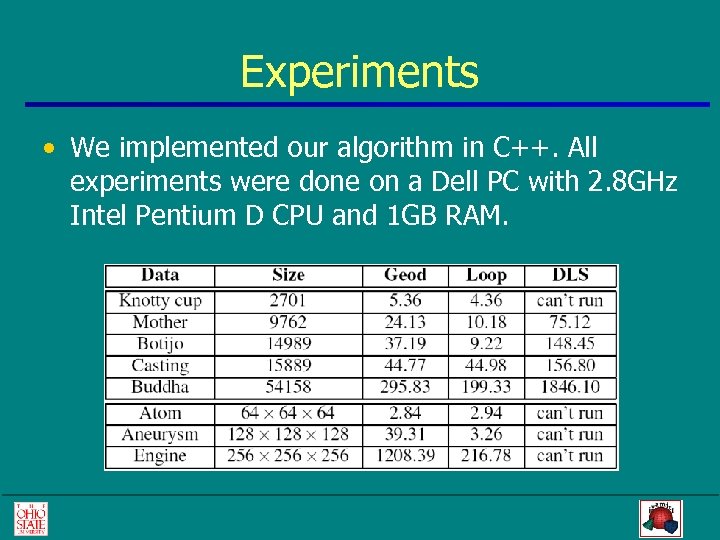Experiments • We implemented our algorithm in C++. All experiments were done on a Dell PC with 2. 8 GHz Intel Pentium D CPU and 1 GB RAM.

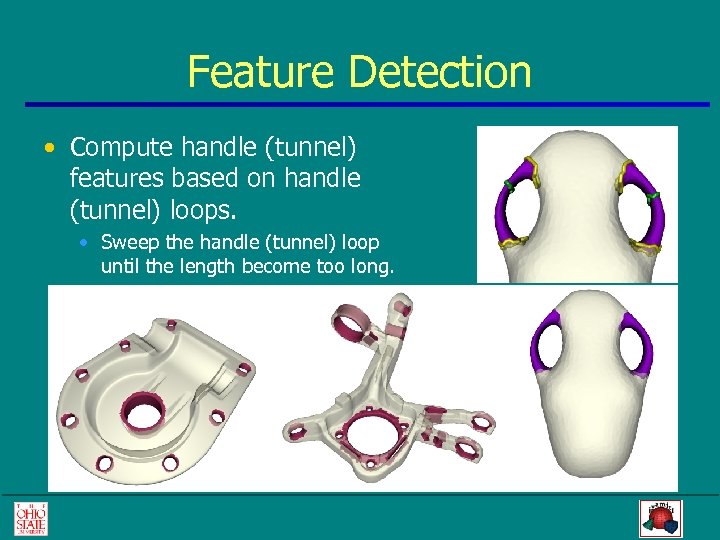Feature Detection • Compute handle (tunnel) features based on handle (tunnel) loops. • Sweep the handle (tunnel) loop until the length become too long.

Topological simplification

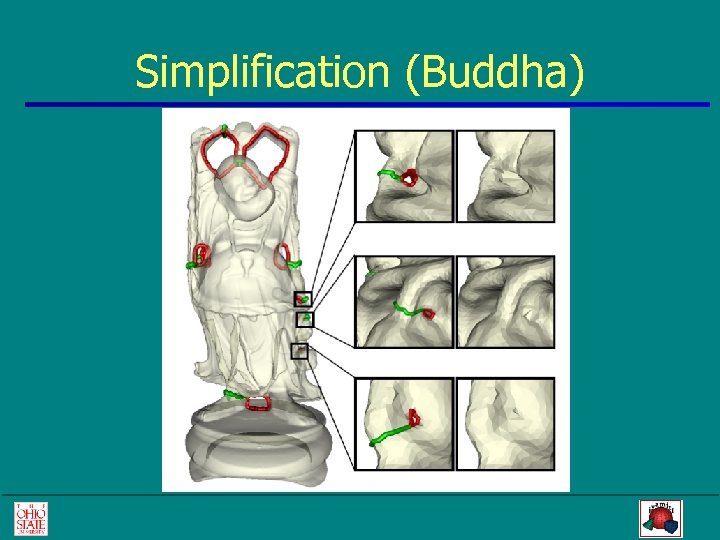Simplification (Buddha)

Conclusions and future work • • A simple, topologically correct algorithm for handles and tunnels. Mathematical proof of geometric qualities of the loops? What about surfaces with boundaries? Handletunnel software available from http: //www. cse. ohio-state. edu/~tamaldey/handle. html

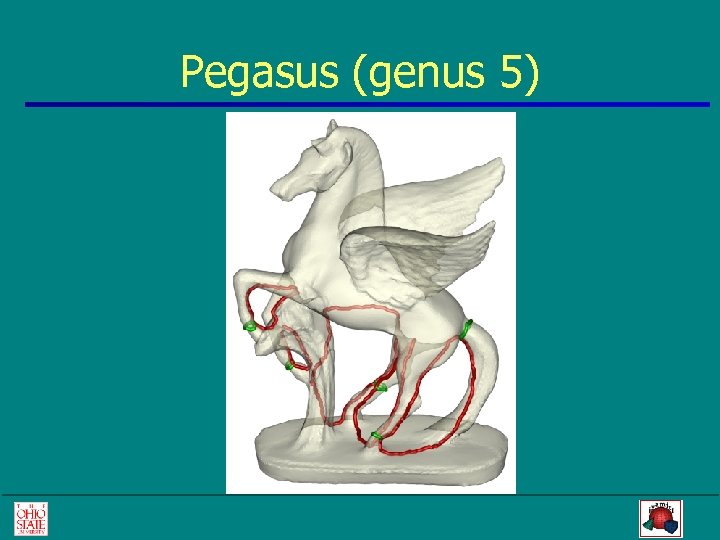Pegasus (genus 5)

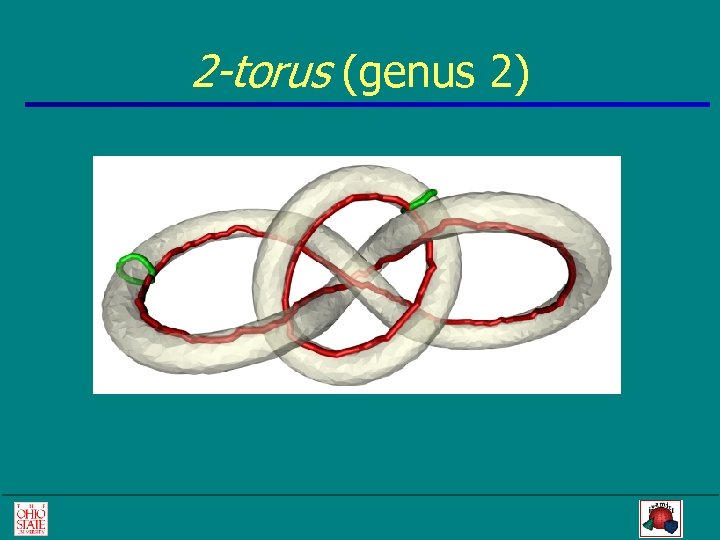2 -torus (genus 2)