b50a1ab3a34401a065f420eb1976eab9.ppt
- Количество слайдов: 17

Computer Science Web as a graph Anna Karpovsky 1

Anna Karpovsky: Motivation Web Search and more accurate topic-classification algorithms, enumerating q emergent cybercommunities Computer Science Is Web graph really random? q Can it be described by Erdos-Renyi or Watts. Strogatz Models? q Web graph is a fascinating object of study =Unregulated growth =Variety =Improved Web algorithms =Sociological information 2
Anna Karpovsky: Outline They are both driven by the presence of certain structures in the Web graph. q These structures appear to be fundamental by q product of the manner in which q Web content is created Computer Science HITS algorithm + Trawling Web graph properties Random graph models 3

Anna Karpovsky: HITS Algorithm: revisited Power iteration to AAT, converge to principle eigenvalues, weights are q intrinsic feature of collection of linked pages. Pages with large weights represent a very dense pattern of q linkage form pages of large hub weight to pages of large authority weight. Computer Science Sampling step: =Root set (200 pages) =Base set (1000 -3000 pages) Weight-propagation step =Authority weight: =Hub weight: =Compact way: 4
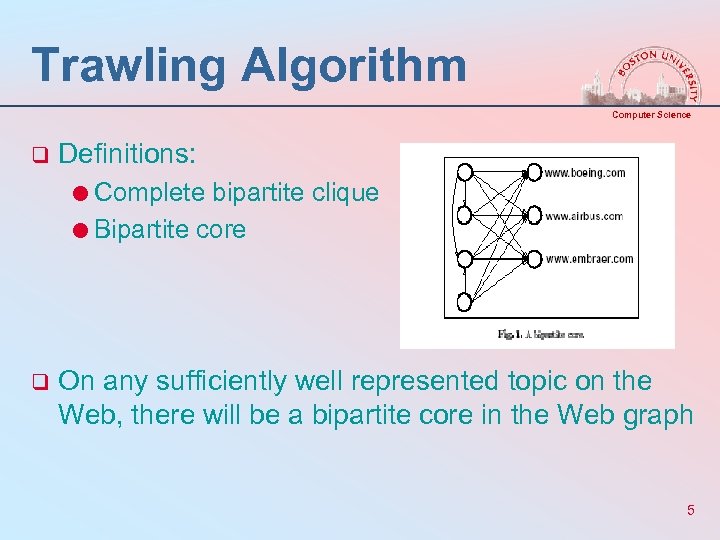
Trawling Algorithm Computer Science q Definitions: =Complete bipartite clique =Bipartite core q On any sufficiently well represented topic on the Web, there will be a bipartite core in the Web graph 5

Elimination-generation paradigm q Computer Science Elimination =Necessary conditions – elimination filters q Generation =Identify barely-qualifying nodes – generation filter 6

Anna Karpovsky: Properties The probability of finding documents with a large number if links is rather significant, the q network connectivity being dominated by highly connected web pages. The probability of finding very popular addresses, to which a large number of other documents point, is a nonnegligible, an indication of the flocking sociology of www. While the owner of each web page has completely Computer Science Degree distribution =Prob(D=i) proportional to 1/i^a – power law =Prob of finding documents with a large number of links and finding very popular addresses is rather significant 7

Properties Computer Science q Number of bipartite cores =Experiments generated well over 100, 000 bipartite cores q Diameter of the web graph = 19 links 8

Random Graph Models Computer Science q Erdos-Renyi Model =N nodes, each pair of nodes is connected with probability p q Watts-Strogatz Model =N nodes form regular lattice. With probability p, each edge is rewired randomly. 9

Traditional Random Graph Models q Computer Science Random Graph =Degree distribution - Poisson or binomial =Number of bipartite cores - Negligible =Number of vertices - Fixed =Connectivity - Random and uniform 10

Anna Karpovsky: Copying process Intuition: author decides to create a new web page, more likely to choose larger q topics. New viewpoint about the topic will probably link to many pages “within” the topic, but also probably q introduce a new spin on the topic, linking to some new pages whose q connection to the topic previously unrecognized Computer Science Create and delete nodes at random =Linear growth – links available right away =Exponential growth – only see the previous “epochs” of pages With some probability, b, add k edges from v to random nodes With probability 1 -b, copy k edges from randomly chosen node to v q Two probabilistic processes: which to copy from and how many to copy 11

Anna Karpovsky: ACL(Aiello, Chung, Lu) Power-law for degrees is an intrinsic feature, rather than emerging Computer Science q Degree sequence is given by a power-law – fixes number of vertices and edges Do not explain large number of bipartite cliques observed in the web Not clear how to adopt to evolving a is the logarithm of the size of the graph and b can be regarded as the loggraph log growth rate of the graph, y vertices of degree x q Set is constructed with as many copies of each vertex as its degree q Random matching in this set is chosen 12

Anna Karpovsky: Scale-free Model Power law observed describes systems of different sizes at q different stages of their development Computer Science Preferential connectivity =Higher prob to be linked to a vertex that already has a large number of connections - (kj) = ki/ kj =Independent of time 13

Analysis on number of cliques q Computer Science Evolving copying models =There are many (t^ ) large cliques =Idea: Let vt’ called a leader if at least one of its d out -links is chosen uniformly. Let v be duplicator if it copies all d of its out-links. On each epoch there is some probability that at least one vertex copies from vt’. So can derive expected number of duplicators of vt’ and its duplicators form a complete bipartite subgraph. 14

Analysis on number of cliques q Computer Science Evolving uniform model =Number of Cij is negligible for ij > i+j =Idea: observed out-degree = 7. 2 15

Analysis on number of cliques q Computer Science Cliques in the ACL model =Number of Cij is constant for i > 2/( -2) =Idea: Summing over all i-tuples and j-tuples of vertices, the probability that all the edges exist between them. We know: maximum degree of a vertex is given by exp( / ) (0<= logy = - logx) and the probability that a vertex has degree d is given by exp( )/d^ . 16

Comments Computer Science Links are not invariant in time q Documents are not stable q Hierarchical structure of the web pages q 17
b50a1ab3a34401a065f420eb1976eab9.ppt