e51a223f3c3c247cd3b099446024d8d2.ppt
- Количество слайдов: 64
 Computer Science&Technology School of Shandong University Guide to Information Security Chapter 10 – Key Management and Other Public Key Cryptosystems Instructor: Hou Mengbo Email: houmb AT sdu. edu. cn Office: Information Security Research Group
Computer Science&Technology School of Shandong University Guide to Information Security Chapter 10 – Key Management and Other Public Key Cryptosystems Instructor: Hou Mengbo Email: houmb AT sdu. edu. cn Office: Information Security Research Group
 Key Management • public-key encryption helps address key distribution problems • have two aspects of this: – distribution of public keys – use of public-key encryption to distribute secret keys
Key Management • public-key encryption helps address key distribution problems • have two aspects of this: – distribution of public keys – use of public-key encryption to distribute secret keys
 Distribution of Public Keys • can be considered as using one of: – Public announcement – Publicly available directory – Public-key authority – Public-key certificates
Distribution of Public Keys • can be considered as using one of: – Public announcement – Publicly available directory – Public-key authority – Public-key certificates
 Public Announcement • users distribute public keys to recipients or broadcast to community at large – eg. append PGP keys to email messages or post to news groups or email list • major weakness is forgery – anyone can create a key claiming to be someone else and broadcast it – can masquerade as claimed user until forgery is discovered
Public Announcement • users distribute public keys to recipients or broadcast to community at large – eg. append PGP keys to email messages or post to news groups or email list • major weakness is forgery – anyone can create a key claiming to be someone else and broadcast it – can masquerade as claimed user until forgery is discovered
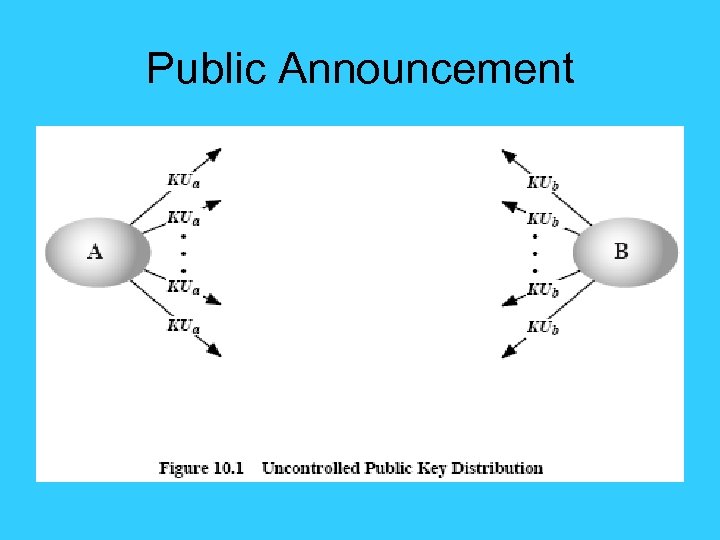 Public Announcement
Public Announcement
 Publicly Available Directory • can obtain greater security by registering keys with a public directory • directory must be trusted with properties: – contains {name, public-key} entries – participants register securely with directory – participants can replace key at any time – directory is periodically published – directory can be accessed electronically • still vulnerable to tampering or forgery
Publicly Available Directory • can obtain greater security by registering keys with a public directory • directory must be trusted with properties: – contains {name, public-key} entries – participants register securely with directory – participants can replace key at any time – directory is periodically published – directory can be accessed electronically • still vulnerable to tampering or forgery
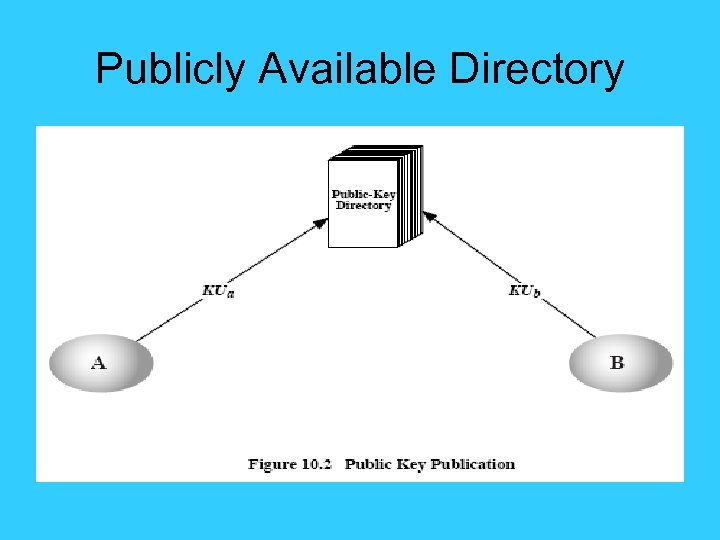 Publicly Available Directory
Publicly Available Directory
 Public-Key Authority • improve security by tightening control over distribution of keys from directory • has properties of directory • and requires users to know public key for the directory • then users interact with directory to obtain any desired public key securely • Weakness: does require real-time access to directory when keys are needed
Public-Key Authority • improve security by tightening control over distribution of keys from directory • has properties of directory • and requires users to know public key for the directory • then users interact with directory to obtain any desired public key securely • Weakness: does require real-time access to directory when keys are needed
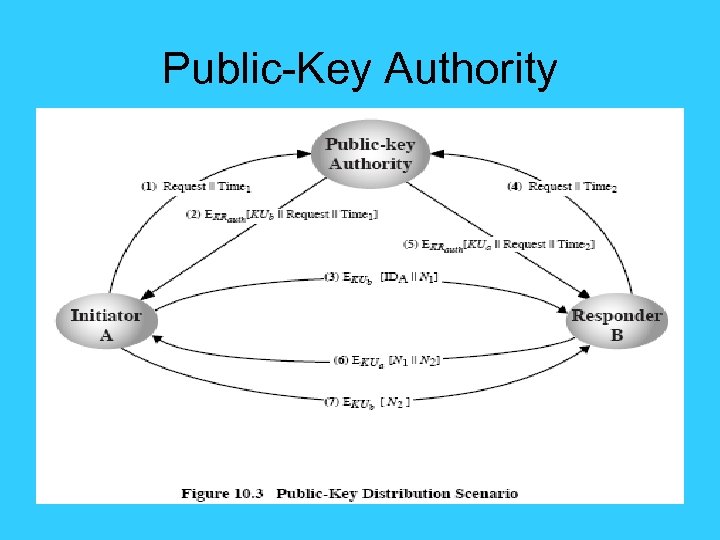 Public-Key Authority
Public-Key Authority
 Public-Key Certificates • certificates allow key exchange without real-time access to public-key authority • a certificate binds identity to public key – usually with other info such as period of validity, rights of use etc • with all contents signed by a trusted Public-Key or Certificate Authority (CA) • can be verified by anyone who knows the public-key authorities public-key
Public-Key Certificates • certificates allow key exchange without real-time access to public-key authority • a certificate binds identity to public key – usually with other info such as period of validity, rights of use etc • with all contents signed by a trusted Public-Key or Certificate Authority (CA) • can be verified by anyone who knows the public-key authorities public-key
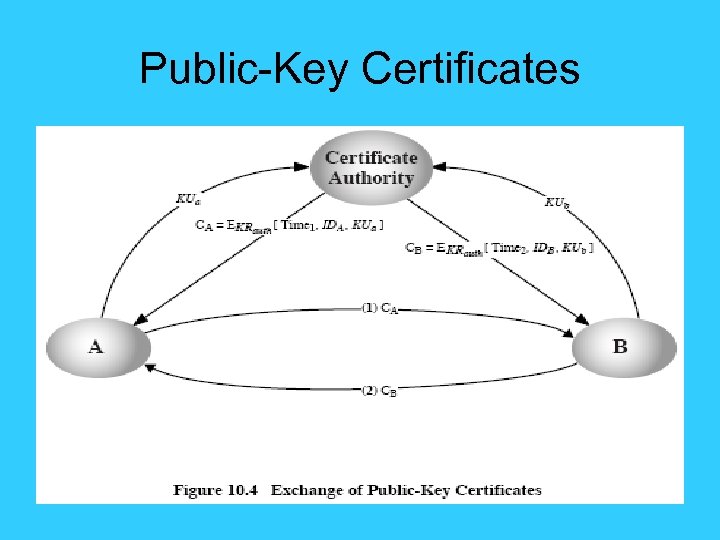 Public-Key Certificates
Public-Key Certificates
 Public-Key Distribution of Secret Keys • use previous methods to obtain public-key, can use for secrecy or authentication • but public-key algorithms are slow, so usually want to use private-key encryption to protect message contents, hence need a session key • have several alternatives for negotiating a suitable session key.
Public-Key Distribution of Secret Keys • use previous methods to obtain public-key, can use for secrecy or authentication • but public-key algorithms are slow, so usually want to use private-key encryption to protect message contents, hence need a session key • have several alternatives for negotiating a suitable session key.
 Simple Secret Key Distribution • proposed by Merkle in 1979 – A generates a new temporary public key pair – A sends B the public key and their identity – B generates a session key K sends it to A encrypted using the supplied public key – A decrypts the session key and both use
Simple Secret Key Distribution • proposed by Merkle in 1979 – A generates a new temporary public key pair – A sends B the public key and their identity – B generates a session key K sends it to A encrypted using the supplied public key – A decrypts the session key and both use
 In-the-middle Attack • problem is that an opponent can intercept and impersonate both halves of protocol • Attacker E in the middle 1. A B: KUa||IDa 2. E B: replace KUa||IDa with KUe|| IDa 3. B A: EKUe[Ks] 4. E A: replace EKUe[Ks] with EKUa[Ks]
In-the-middle Attack • problem is that an opponent can intercept and impersonate both halves of protocol • Attacker E in the middle 1. A B: KUa||IDa 2. E B: replace KUa||IDa with KUe|| IDa 3. B A: EKUe[Ks] 4. E A: replace EKUe[Ks] with EKUa[Ks]
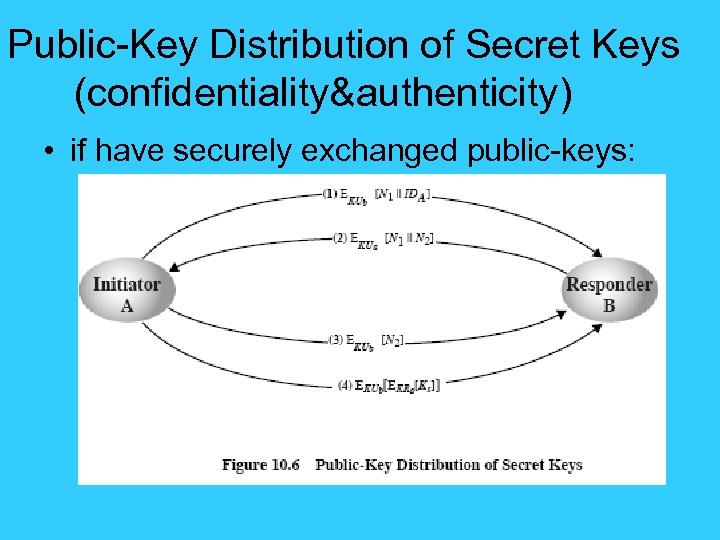 Public-Key Distribution of Secret Keys (confidentiality&authenticity) • if have securely exchanged public-keys:
Public-Key Distribution of Secret Keys (confidentiality&authenticity) • if have securely exchanged public-keys:
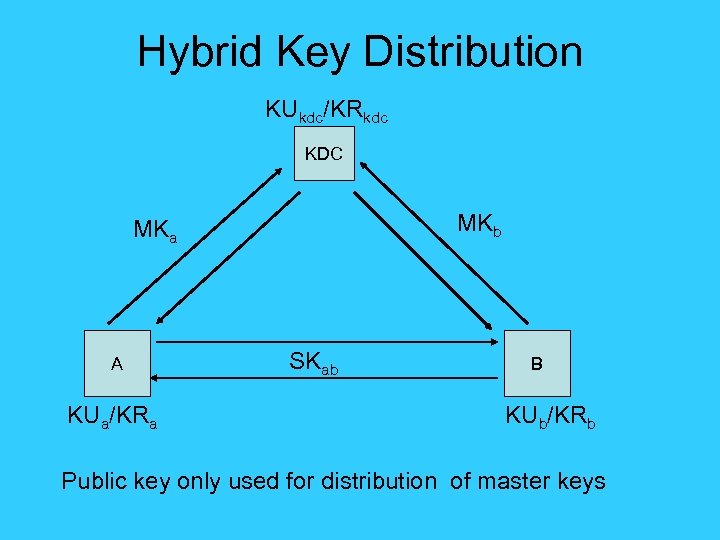 Hybrid Key Distribution KUkdc/KRkdc KDC MKb MKa A KUa/KRa SKab B KUb/KRb Public key only used for distribution of master keys
Hybrid Key Distribution KUkdc/KRkdc KDC MKb MKa A KUa/KRa SKab B KUb/KRb Public key only used for distribution of master keys
 Diffie-Hellman Key Exchange • first public-key type scheme proposed • by Diffie & Hellman in 1976 along with the exposition of public key concepts – note: now know that James Ellis (UK CESG) secretly proposed the concept in 1970 • is a practical method for public exchange of a secret key • used in a number of commercial products
Diffie-Hellman Key Exchange • first public-key type scheme proposed • by Diffie & Hellman in 1976 along with the exposition of public key concepts – note: now know that James Ellis (UK CESG) secretly proposed the concept in 1970 • is a practical method for public exchange of a secret key • used in a number of commercial products
 Diffie-Hellman Key Exchange • a public-key distribution scheme – cannot be used to exchange an arbitrary message – rather it can establish a common key – known only to the two participants • value of key depends on the participants (and their private and public key information) • based on exponentiation in a finite (Galois) field (modulo a prime or a polynomial) - easy • security relies on the difficulty of computing discrete logarithms (similar to factoring) – hard
Diffie-Hellman Key Exchange • a public-key distribution scheme – cannot be used to exchange an arbitrary message – rather it can establish a common key – known only to the two participants • value of key depends on the participants (and their private and public key information) • based on exponentiation in a finite (Galois) field (modulo a prime or a polynomial) - easy • security relies on the difficulty of computing discrete logarithms (similar to factoring) – hard
 Diffie-Hellman Setup • all users agree on global parameters: – large prime integer q – α a primitive root mod q • each user (eg. A) generates their key – chooses a secret key (number): x. A < q x. A – compute their public key: y. A = α mod q • each user makes public that key y. A
Diffie-Hellman Setup • all users agree on global parameters: – large prime integer q – α a primitive root mod q • each user (eg. A) generates their key – chooses a secret key (number): x. A < q x. A – compute their public key: y. A = α mod q • each user makes public that key y. A
 Diffie-Hellman Key Exchange • shared session key for users A & B is KAB: x. A. x. B KAB = α mod q x. B = y. A mod q (which B can compute) x. A = y. B mod q (which A can compute) • KAB is used as session key in private-key encryption scheme between Alice and Bob • if Alice and Bob subsequently communicate, they will have the same key as before, unless they choose new public-keys • attacker needs an x, must solve discrete log
Diffie-Hellman Key Exchange • shared session key for users A & B is KAB: x. A. x. B KAB = α mod q x. B = y. A mod q (which B can compute) x. A = y. B mod q (which A can compute) • KAB is used as session key in private-key encryption scheme between Alice and Bob • if Alice and Bob subsequently communicate, they will have the same key as before, unless they choose new public-keys • attacker needs an x, must solve discrete log
 Diffie-Hellman Example • users Alice & Bob who wish to swap keys: • agree on prime q=353 and α=3 • select random secret keys: – A chooses x. A=97, B chooses x. B=233 • compute public keys: 97 – y. A=3 mod 353 = 40 (Alice) 233 – y. B=3 mod 353 = 248 (Bob) • compute shared session key as: x 97 KAB= y. B A mod 353 = 248 = 160 x 233 KAB= y. A B mod 353 = 40 = 160 (Alice) (Bob)
Diffie-Hellman Example • users Alice & Bob who wish to swap keys: • agree on prime q=353 and α=3 • select random secret keys: – A chooses x. A=97, B chooses x. B=233 • compute public keys: 97 – y. A=3 mod 353 = 40 (Alice) 233 – y. B=3 mod 353 = 248 (Bob) • compute shared session key as: x 97 KAB= y. B A mod 353 = 248 = 160 x 233 KAB= y. A B mod 353 = 40 = 160 (Alice) (Bob)
 Key Exchange Protocols • users could create random private/public D -H keys each time they communicate • users could create a known private/public D-H key and publish in a directory, then consulted and used to securely communicate with them • both of these are vulnerable to a meet-inthe-Middle Attack • authentication of the keys is needed
Key Exchange Protocols • users could create random private/public D -H keys each time they communicate • users could create a known private/public D-H key and publish in a directory, then consulted and used to securely communicate with them • both of these are vulnerable to a meet-inthe-Middle Attack • authentication of the keys is needed
 Elliptic Curve Cryptography • majority of public-key crypto (RSA, D-H) use either integer or polynomial arithmetic with very large numbers/polynomials • imposes a significant load in storing and processing keys and messages • an alternative is to use elliptic curves • offers same security with smaller bit sizes
Elliptic Curve Cryptography • majority of public-key crypto (RSA, D-H) use either integer or polynomial arithmetic with very large numbers/polynomials • imposes a significant load in storing and processing keys and messages • an alternative is to use elliptic curves • offers same security with smaller bit sizes
 Real Elliptic Curves • an elliptic curve is defined by an equation in two variables x & y, with coefficients • consider a cubic elliptic curve of form – y 2 = x 3 + ax + b – where x, y, a, b are all real numbers – also define zero point O • have addition operation for elliptic curve – geometrically sum of Q+R is reflection of intersection R
Real Elliptic Curves • an elliptic curve is defined by an equation in two variables x & y, with coefficients • consider a cubic elliptic curve of form – y 2 = x 3 + ax + b – where x, y, a, b are all real numbers – also define zero point O • have addition operation for elliptic curve – geometrically sum of Q+R is reflection of intersection R
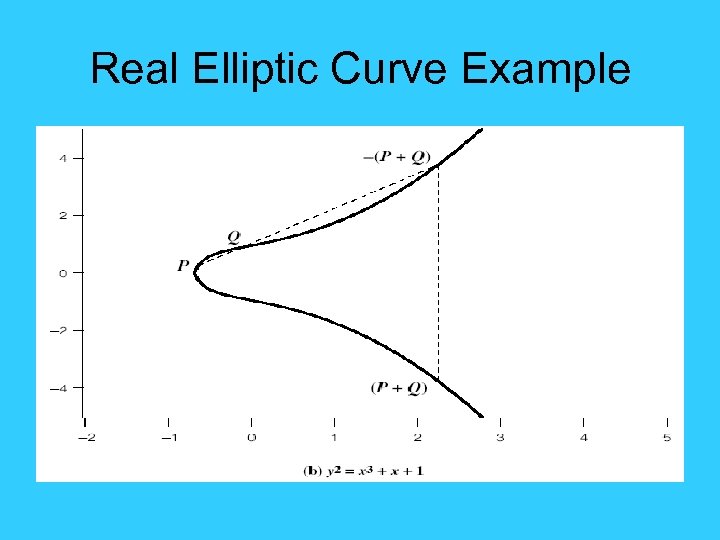 Real Elliptic Curve Example
Real Elliptic Curve Example
 Finite Elliptic Curves • Elliptic curve cryptography uses curves whose variables & coefficients are finite • have two families commonly used: – prime curves Ep(a, b) defined over Zp • use integers modulo a prime • best in software – binary curves E 2 m(a, b) defined over GF(2 n) • use polynomials with binary coefficients • best in hardware
Finite Elliptic Curves • Elliptic curve cryptography uses curves whose variables & coefficients are finite • have two families commonly used: – prime curves Ep(a, b) defined over Zp • use integers modulo a prime • best in software – binary curves E 2 m(a, b) defined over GF(2 n) • use polynomials with binary coefficients • best in hardware
 Elliptic Curve Cryptography • ECC addition is analog of modulo multiply • ECC repeated addition is analog of modulo exponentiation • need “hard” problem equiv to discrete log – Q=k. P, where Q, P belong to a prime curve – is “easy” to compute Q given k, P – but “hard” to find k given Q, P – known as the elliptic curve logarithm problem • Certicom example: E 23(9, 17)
Elliptic Curve Cryptography • ECC addition is analog of modulo multiply • ECC repeated addition is analog of modulo exponentiation • need “hard” problem equiv to discrete log – Q=k. P, where Q, P belong to a prime curve – is “easy” to compute Q given k, P – but “hard” to find k given Q, P – known as the elliptic curve logarithm problem • Certicom example: E 23(9, 17)
 ECC Diffie-Hellman • can do key exchange analogous to D-H • users select a suitable curve Ep(a, b) • select base point G=(x 1, y 1) with large order n s. t. n. G=O • A & B select private keys n. A
ECC Diffie-Hellman • can do key exchange analogous to D-H • users select a suitable curve Ep(a, b) • select base point G=(x 1, y 1) with large order n s. t. n. G=O • A & B select private keys n. A
 ECC Encryption/Decryption • several alternatives, will consider simplest • must first encode any message M as a point on the elliptic curve Pm • select suitable curve & point G as in D-H • each user chooses private key n. A
ECC Encryption/Decryption • several alternatives, will consider simplest • must first encode any message M as a point on the elliptic curve Pm • select suitable curve & point G as in D-H • each user chooses private key n. A
 ECC Security • relies on elliptic curve logarithm problem • fastest method is “Pollard rho method” • compared to factoring, can use much smaller key sizes than with RSA etc • for equivalent key lengths computations are roughly equivalent • hence for similar security ECC offers significant computational advantages
ECC Security • relies on elliptic curve logarithm problem • fastest method is “Pollard rho method” • compared to factoring, can use much smaller key sizes than with RSA etc • for equivalent key lengths computations are roughly equivalent • hence for similar security ECC offers significant computational advantages
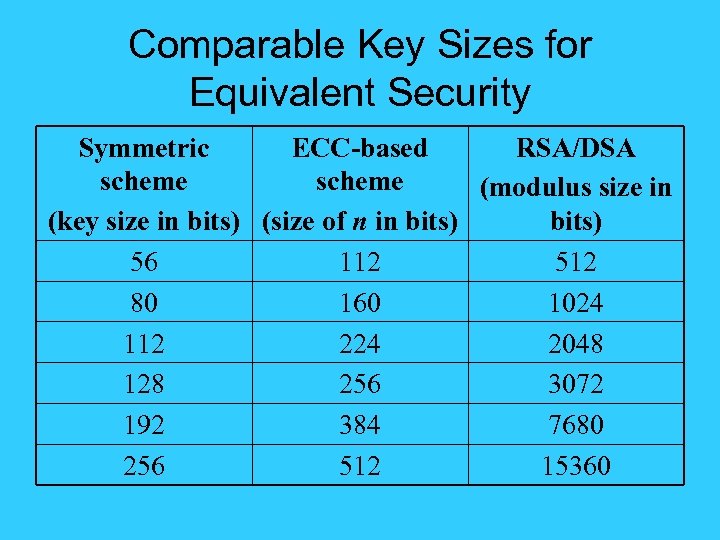 Comparable Key Sizes for Equivalent Security Symmetric ECC-based RSA/DSA scheme (modulus size in (key size in bits) (size of n in bits) 56 112 512 80 160 1024 112 224 2048 128 256 3072 192 384 7680 256 512 15360
Comparable Key Sizes for Equivalent Security Symmetric ECC-based RSA/DSA scheme (modulus size in (key size in bits) (size of n in bits) 56 112 512 80 160 1024 112 224 2048 128 256 3072 192 384 7680 256 512 15360
 Summary • have considered: – distribution of public keys – public-key distribution of secret keys – Diffie-Hellman key exchange – Elliptic Curve cryptography
Summary • have considered: – distribution of public keys – public-key distribution of secret keys – Diffie-Hellman key exchange – Elliptic Curve cryptography
 Computer Science&Technology School of Shandong University 信息安全导论 (第 10章 附: 椭圆曲线密码体制 ) Instructor: Hou. Mengbo 侯孟波 Email: houmb@sdu. edu. cn Office: Information Security Research Office. Main. Building Room 942 of SDU(South Section)
Computer Science&Technology School of Shandong University 信息安全导论 (第 10章 附: 椭圆曲线密码体制 ) Instructor: Hou. Mengbo 侯孟波 Email: houmb@sdu. edu. cn Office: Information Security Research Office. Main. Building Room 942 of SDU(South Section)
 椭圆曲线的定义 一条椭圆曲线是在射影平面上满足Weierstrass方程 : Y 2 Z+a 1 XYZ+a 3 YZ 2=X 3+a 2 X 2 Z+a 4 XZ 2+a 6 Z 3 --[1] 的所有点的集合,且曲线上的每个点都是非奇异( 或光滑)的。 所谓“非奇异”或“光滑”的,在数学中是指曲线上任意 一点的偏导数Fx(x, y, z),Fy(x, y, z),Fz(x, y, z)不能同时 为 0。即满足方程的任意一点都存在切线。
椭圆曲线的定义 一条椭圆曲线是在射影平面上满足Weierstrass方程 : Y 2 Z+a 1 XYZ+a 3 YZ 2=X 3+a 2 X 2 Z+a 4 XZ 2+a 6 Z 3 --[1] 的所有点的集合,且曲线上的每个点都是非奇异( 或光滑)的。 所谓“非奇异”或“光滑”的,在数学中是指曲线上任意 一点的偏导数Fx(x, y, z),Fy(x, y, z),Fz(x, y, z)不能同时 为 0。即满足方程的任意一点都存在切线。
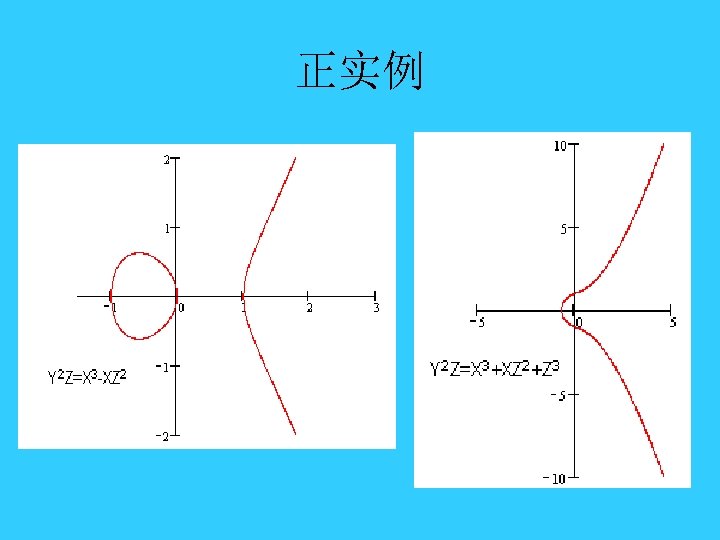 正实例
正实例
![反例 • 下面两个方程都不是椭圆曲线,尽管他们是方程[ 1]的形 式 反例 • 下面两个方程都不是椭圆曲线,尽管他们是方程[ 1]的形 式](https://present5.com/presentation/e51a223f3c3c247cd3b099446024d8d2/image-36.jpg) 反例 • 下面两个方程都不是椭圆曲线,尽管他们是方程[ 1]的形 式
反例 • 下面两个方程都不是椭圆曲线,尽管他们是方程[ 1]的形 式
![椭圆曲线 • 椭圆曲线上有一个无穷远点O∞(0: 1: 0),因为这个点满足方程[1]。 我们在普通平面直角坐标系上,求出椭圆曲线上所有平常点组成的曲 线方程,再加上无穷远点O∞(0: 1: 0),就构成椭圆曲线. 我们设x=X/Z ,y=Y/Z代入方程[1]得到: y 2+a 1 椭圆曲线 • 椭圆曲线上有一个无穷远点O∞(0: 1: 0),因为这个点满足方程[1]。 我们在普通平面直角坐标系上,求出椭圆曲线上所有平常点组成的曲 线方程,再加上无穷远点O∞(0: 1: 0),就构成椭圆曲线. 我们设x=X/Z ,y=Y/Z代入方程[1]得到: y 2+a 1](https://present5.com/presentation/e51a223f3c3c247cd3b099446024d8d2/image-37.jpg) 椭圆曲线 • 椭圆曲线上有一个无穷远点O∞(0: 1: 0),因为这个点满足方程[1]。 我们在普通平面直角坐标系上,求出椭圆曲线上所有平常点组成的曲 线方程,再加上无穷远点O∞(0: 1: 0),就构成椭圆曲线. 我们设x=X/Z ,y=Y/Z代入方程[1]得到: y 2+a 1 xy+a 3 y = x 3+a 2 x 2+a 4 x+a 6 ---[2] 也就是说满足方程[2]的光滑曲线加上一个无穷远点O∞,组成 了椭圆曲线。 • 由椭圆曲线的定义可以知道,椭圆曲线是光滑的,所以椭圆曲线上的 平常点都有切线。而切线最重要的一个参数就是斜率k。
椭圆曲线 • 椭圆曲线上有一个无穷远点O∞(0: 1: 0),因为这个点满足方程[1]。 我们在普通平面直角坐标系上,求出椭圆曲线上所有平常点组成的曲 线方程,再加上无穷远点O∞(0: 1: 0),就构成椭圆曲线. 我们设x=X/Z ,y=Y/Z代入方程[1]得到: y 2+a 1 xy+a 3 y = x 3+a 2 x 2+a 4 x+a 6 ---[2] 也就是说满足方程[2]的光滑曲线加上一个无穷远点O∞,组成 了椭圆曲线。 • 由椭圆曲线的定义可以知道,椭圆曲线是光滑的,所以椭圆曲线上的 平常点都有切线。而切线最重要的一个参数就是斜率k。
 例 • 例1:求椭圆曲线方程y 2+a 1 xy+a 3 y=x 3+a 2 x 2+a 4 x+a 6上, 平常点A(x, y)的切线的斜率k。 解:令F(x, y)= y 2+a 1 xy+a 3 y-x 3 -a 2 x 2 -a 4 x-a 6 求偏导数 Fx(x, y)= a 1 y-3 x 2 -2 a 2 x-a 4 Fy(x, y)= 2 y+a 1 x +a 3 则导数为: f'(x)=- Fx(x, y)/ Fy(x, y)=-( a 1 y-3 x 2 -2 a 2 x-a 4)/(2 y+a 1 x +a 3) = (3 x 2+2 a 2 x+a 4 -a 1 y) /(2 y+a 1 x +a 3) 所以k=(3 x 2+2 a 2 x+a 4 -a 1 y) /(2 y+a 1 x +a 3) -----[3]
例 • 例1:求椭圆曲线方程y 2+a 1 xy+a 3 y=x 3+a 2 x 2+a 4 x+a 6上, 平常点A(x, y)的切线的斜率k。 解:令F(x, y)= y 2+a 1 xy+a 3 y-x 3 -a 2 x 2 -a 4 x-a 6 求偏导数 Fx(x, y)= a 1 y-3 x 2 -2 a 2 x-a 4 Fy(x, y)= 2 y+a 1 x +a 3 则导数为: f'(x)=- Fx(x, y)/ Fy(x, y)=-( a 1 y-3 x 2 -2 a 2 x-a 4)/(2 y+a 1 x +a 3) = (3 x 2+2 a 2 x+a 4 -a 1 y) /(2 y+a 1 x +a 3) 所以k=(3 x 2+2 a 2 x+a 4 -a 1 y) /(2 y+a 1 x +a 3) -----[3]
 椭圆曲线上的加法 • 运算法则:任意取椭圆曲线上两点P、Q (若P、Q 两点重合,则做P点的切线)做直线交于椭圆曲线 的另一点R’,过R’做y轴的平行线交于R。 • 我们规定P+Q=R。
椭圆曲线上的加法 • 运算法则:任意取椭圆曲线上两点P、Q (若P、Q 两点重合,则做P点的切线)做直线交于椭圆曲线 的另一点R’,过R’做y轴的平行线交于R。 • 我们规定P+Q=R。
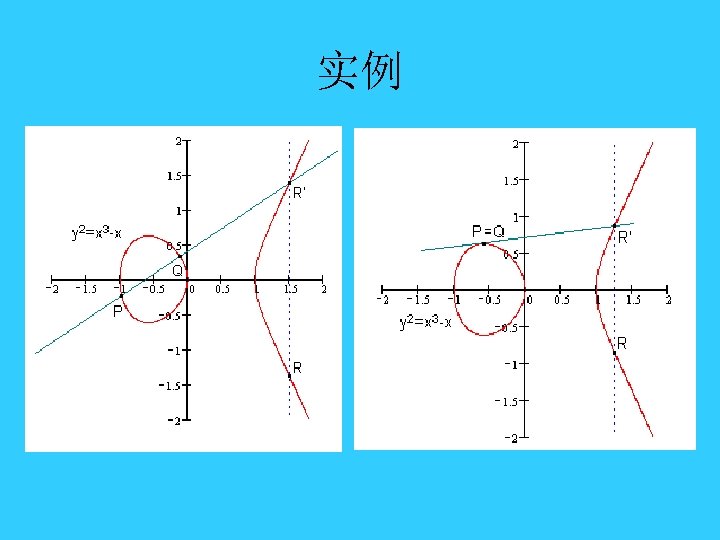 实例
实例
 零元/负元 • 根据运算法则,椭圆曲线无穷远点O∞与椭圆曲线上一点P 的连线交于P’,过P’作y轴的平行线交于P • 所以有:无穷远点 O∞+ P = P 。无穷远点 O∞的作用与 普通加法中零的作用相当。 • 我们把无穷远点 O∞ 称为 零元。同时我们把P’称为P的 负元(记作-P)。(参见下图)
零元/负元 • 根据运算法则,椭圆曲线无穷远点O∞与椭圆曲线上一点P 的连线交于P’,过P’作y轴的平行线交于P • 所以有:无穷远点 O∞+ P = P 。无穷远点 O∞的作用与 普通加法中零的作用相当。 • 我们把无穷远点 O∞ 称为 零元。同时我们把P’称为P的 负元(记作-P)。(参见下图)
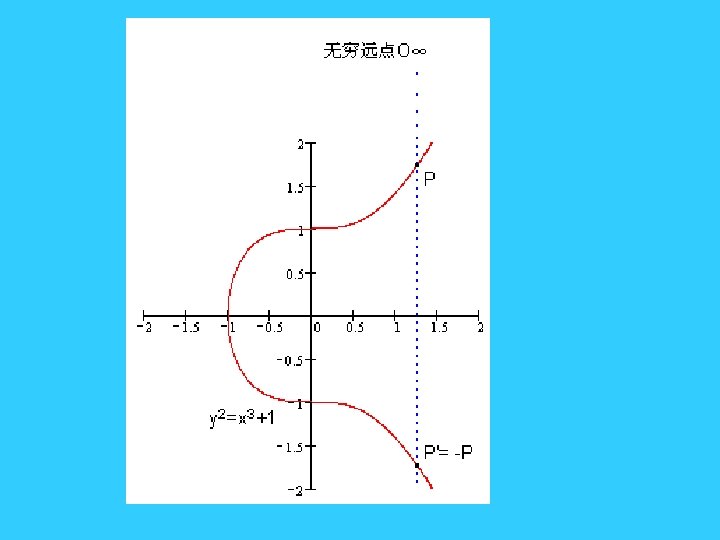
 • 根据这个法则,可以得到如下结论 :如果椭圆曲 线上的三个点A、B、C,处于同一条直线上,那么 他们的和等于零元,即A+B+C= O∞ • k个相同的点P相加,我们记作k. P。如下图:P+P+P = 2 P+P = 3 P。
• 根据这个法则,可以得到如下结论 :如果椭圆曲 线上的三个点A、B、C,处于同一条直线上,那么 他们的和等于零元,即A+B+C= O∞ • k个相同的点P相加,我们记作k. P。如下图:P+P+P = 2 P+P = 3 P。
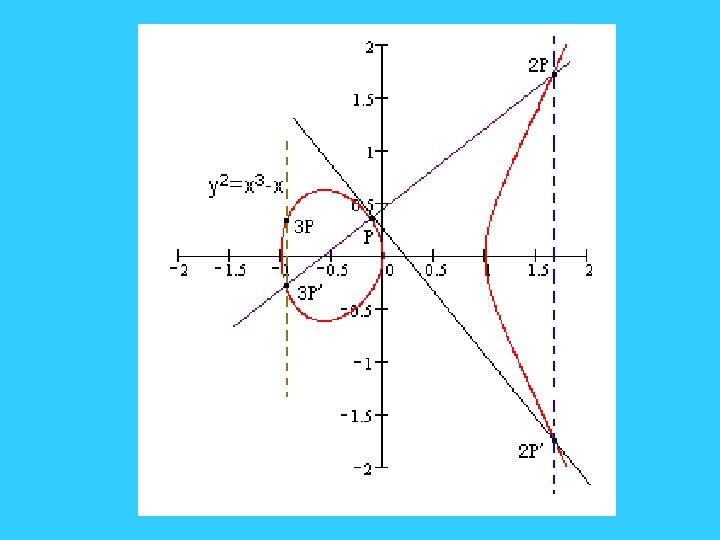
 例:求椭圆曲线方程y 2+a 1 xy+a 3 y=x 3+a 2 x 2+a 4 x+a 6上,平常 点P(x 1, y 1),Q(x 2, y 2)的和R(x 4, y 4)的坐标。 ( R=P+Q ) 解:(1)先求点-R(x 3, y 3) P, Q, -R三点共线,设共线方程为y=kx+b, 其中若P≠Q, 则直线斜 率k=(y 1 -y 2)/(x 1 -x 2). 若P=Q, 则直线为椭圆曲线的切线,故 k=(3 x 2+2 a 2 x+a 4 -a 1 y) /(2 y+a 1 x+a 3) 因此P, Q, -R三点的坐标值就是方程组: y 2+a 1 xy+a 3 y=x 3+a 2 x 2+a 4 x+a 6 --[1] y=(kx+b) --[2] 的解。 将[2],代入[1] 有 (kx+b)2+a 1 x(kx+b)+a 3(kx+b) =x 3+a 2 x 2+a 4 x+a 6 ---[3] 对[3]化为一般方程,根据三次方程根与系数关系(当三次项系 数为 1时;-x 1 x 2 x 3 等于常数项系数, x 1 x 2+x 2 x 3+x 3 x 1等于一次项系数, -(x 1+x 2+x 3)等于二次项系数。) 所以-(x 1+x 2+x 3)=a 2 -ka 1 -k 2 x 3=k 2+ka 1+a 2+x 1+x 2; ----求出点R的横坐标 因为k=(y 1 -y 3)/(x 1 -x 3) 故 y 3=y 1 -k(x 1 -x 3); ----求出点R的纵坐标
例:求椭圆曲线方程y 2+a 1 xy+a 3 y=x 3+a 2 x 2+a 4 x+a 6上,平常 点P(x 1, y 1),Q(x 2, y 2)的和R(x 4, y 4)的坐标。 ( R=P+Q ) 解:(1)先求点-R(x 3, y 3) P, Q, -R三点共线,设共线方程为y=kx+b, 其中若P≠Q, 则直线斜 率k=(y 1 -y 2)/(x 1 -x 2). 若P=Q, 则直线为椭圆曲线的切线,故 k=(3 x 2+2 a 2 x+a 4 -a 1 y) /(2 y+a 1 x+a 3) 因此P, Q, -R三点的坐标值就是方程组: y 2+a 1 xy+a 3 y=x 3+a 2 x 2+a 4 x+a 6 --[1] y=(kx+b) --[2] 的解。 将[2],代入[1] 有 (kx+b)2+a 1 x(kx+b)+a 3(kx+b) =x 3+a 2 x 2+a 4 x+a 6 ---[3] 对[3]化为一般方程,根据三次方程根与系数关系(当三次项系 数为 1时;-x 1 x 2 x 3 等于常数项系数, x 1 x 2+x 2 x 3+x 3 x 1等于一次项系数, -(x 1+x 2+x 3)等于二次项系数。) 所以-(x 1+x 2+x 3)=a 2 -ka 1 -k 2 x 3=k 2+ka 1+a 2+x 1+x 2; ----求出点R的横坐标 因为k=(y 1 -y 3)/(x 1 -x 3) 故 y 3=y 1 -k(x 1 -x 3); ----求出点R的纵坐标
 (2)利用-R求R 显然有 x 4=x 3= k 2+ka 1+a 2+x 1+x 2; --求出点R的横坐 标 而y 3 y 4 为 x=x 4时 方程y 2+a 1 xy+a 3 y=x 3+a 2 x 2+a 4 x+a 6 的解 化为一般方程y 2+(a 1 x+a 3)y-(x 3+a 2 x 2+a 4 x+a 6)=0 , 根 据二次方程根与系数关系得: -(a 1 x+a 3)=y 3+y 4 故y 4=-y 3 -(a 1 x+a 3)=k(x 1 -x 4)-y 1 -(a 1 x 4+a 3); --求出点R的纵坐标 即: x 4=k 2+ka 1+a 2+x 1+x 2; y 4=k(x 1 -x 4)-y 1 -a 1 x 4 -a 3;
(2)利用-R求R 显然有 x 4=x 3= k 2+ka 1+a 2+x 1+x 2; --求出点R的横坐 标 而y 3 y 4 为 x=x 4时 方程y 2+a 1 xy+a 3 y=x 3+a 2 x 2+a 4 x+a 6 的解 化为一般方程y 2+(a 1 x+a 3)y-(x 3+a 2 x 2+a 4 x+a 6)=0 , 根 据二次方程根与系数关系得: -(a 1 x+a 3)=y 3+y 4 故y 4=-y 3 -(a 1 x+a 3)=k(x 1 -x 4)-y 1 -(a 1 x 4+a 3); --求出点R的纵坐标 即: x 4=k 2+ka 1+a 2+x 1+x 2; y 4=k(x 1 -x 4)-y 1 -a 1 x 4 -a 3;
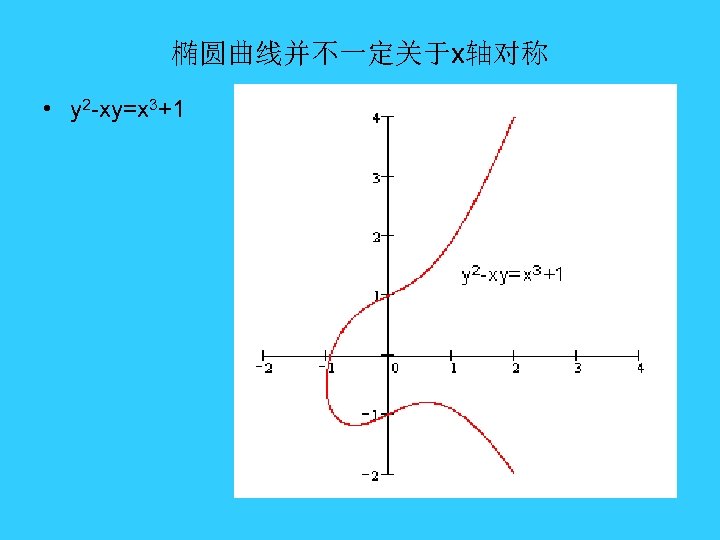 椭圆曲线并不一定关于x轴对称 • y 2 -xy=x 3+1
椭圆曲线并不一定关于x轴对称 • y 2 -xy=x 3+1
 密码学中的椭圆曲线 • 前面学到的椭圆曲线是连续的,并不适合用于加密;必 须把椭圆曲线变成离散的点。 椭圆曲线连续是因为椭圆曲线上点的坐标是实数的 (也就是说前面讲到的椭圆曲线是定义在实数域上的), 实数是连续的,导致了曲线的连续。 • 因此,我们要把椭圆曲线定义在有限域上。
密码学中的椭圆曲线 • 前面学到的椭圆曲线是连续的,并不适合用于加密;必 须把椭圆曲线变成离散的点。 椭圆曲线连续是因为椭圆曲线上点的坐标是实数的 (也就是说前面讲到的椭圆曲线是定义在实数域上的), 实数是连续的,导致了曲线的连续。 • 因此,我们要把椭圆曲线定义在有限域上。
 • 并不是所有的椭圆曲线都适合加密。y 2=x 3+ax+b是一类可以用来加密 的椭圆曲线,也是最为简单的一类。下面我们就把y 2=x 3+ax+b 这条曲 线定义在Fp上: 选择两个满足下列条件的小于p(p为素数)的非负整数 a
• 并不是所有的椭圆曲线都适合加密。y 2=x 3+ax+b是一类可以用来加密 的椭圆曲线,也是最为简单的一类。下面我们就把y 2=x 3+ax+b 这条曲 线定义在Fp上: 选择两个满足下列条件的小于p(p为素数)的非负整数 a
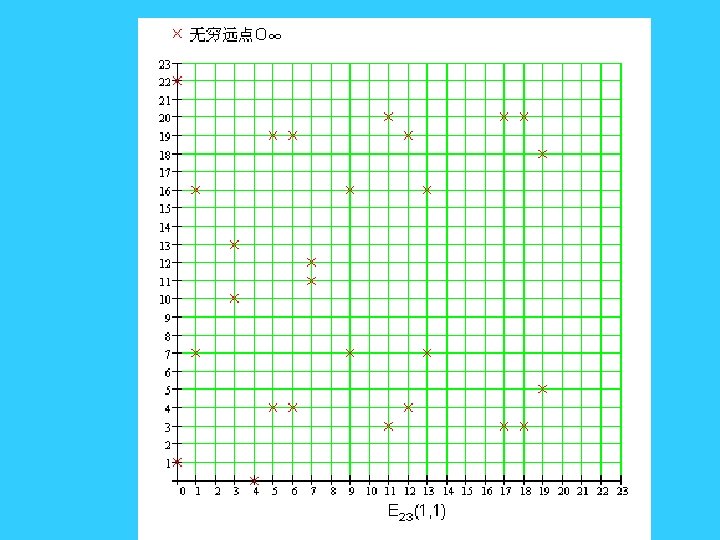
 1。 无穷远点 O∞是零元,有O∞+ O∞= O∞,O∞+P=P 2。 P(x, y)的负元是 (x, -y),有P+(-P)= O∞ 3。 P(x 1, y 1), Q(x 2, y 2)的和R(x 3, y 3) 有如下关系: x 3≡k 2 -x 1 -x 2(mod p) y 3≡k(x 1 -x 3)-y 1(mod p) 其中若P=Q 则 k=(3 x 2+a)/2 y 1 若P≠Q,则k=(y 2 -y 1)/(x 2 -x 1) • 椭圆曲线上的有限交换群Ep(a, b)中点的个数N满足: P+1 -2*P 1/2 <= N <= P+1+ 2*P 1/2 对于大数P, N 约等于ZP 中元素的个数.
1。 无穷远点 O∞是零元,有O∞+ O∞= O∞,O∞+P=P 2。 P(x, y)的负元是 (x, -y),有P+(-P)= O∞ 3。 P(x 1, y 1), Q(x 2, y 2)的和R(x 3, y 3) 有如下关系: x 3≡k 2 -x 1 -x 2(mod p) y 3≡k(x 1 -x 3)-y 1(mod p) 其中若P=Q 则 k=(3 x 2+a)/2 y 1 若P≠Q,则k=(y 2 -y 1)/(x 2 -x 1) • 椭圆曲线上的有限交换群Ep(a, b)中点的个数N满足: P+1 -2*P 1/2 <= N <= P+1+ 2*P 1/2 对于大数P, N 约等于ZP 中元素的个数.
 • 例 已知E 23(1, 1)上两点P(3, 10),Q(9, 7),求1)-P,2)P+Q,3) 2 P。 解 1) –P的值为(3, -10) 2) k=(7 -10)/(9 -3)=-1/2,2的乘法逆元为 12 因为 2*12≡ 1 (mod 23) k≡-1*12 (mod 23) 故 k=11。 x=112 -3 -9=109≡ 17 (mod 23); y=11[3 -(-6)]-10=89≡ 20 (mod 23) 故P+Q的坐标为(17, 20) 3) k=[3(32)+1]/(2*10)=1/4≡ 6 (mod 23) x=62 -3 -3=30≡ 20 (mod 23) y=6(3 -7)-10=-34≡ 12 (mod 23) 故2 P的坐标为(7, 12) • 如果椭圆曲线上一点P,存在最小的正整数n,使得数乘 n. P=O∞,则将n称为P的 阶,若n不存在,我们说P是无限 阶的。 事实上,在有限域上定义的椭圆曲线上所有的点的 阶n都是存在的.
• 例 已知E 23(1, 1)上两点P(3, 10),Q(9, 7),求1)-P,2)P+Q,3) 2 P。 解 1) –P的值为(3, -10) 2) k=(7 -10)/(9 -3)=-1/2,2的乘法逆元为 12 因为 2*12≡ 1 (mod 23) k≡-1*12 (mod 23) 故 k=11。 x=112 -3 -9=109≡ 17 (mod 23); y=11[3 -(-6)]-10=89≡ 20 (mod 23) 故P+Q的坐标为(17, 20) 3) k=[3(32)+1]/(2*10)=1/4≡ 6 (mod 23) x=62 -3 -3=30≡ 20 (mod 23) y=6(3 -7)-10=-34≡ 12 (mod 23) 故2 P的坐标为(7, 12) • 如果椭圆曲线上一点P,存在最小的正整数n,使得数乘 n. P=O∞,则将n称为P的 阶,若n不存在,我们说P是无限 阶的。 事实上,在有限域上定义的椭圆曲线上所有的点的 阶n都是存在的.
![椭圆曲线上简单的加密/解密 • 考虑如下等式: K=k. G [其中 K, G为Ep(a, b)上的点,k为小 于n(n是点G的阶)的整数] 给定k和G,根据加法法则,计算K很容易; 但给定K和G,求k就相对困难了。 这就是椭圆曲线加密算法采用的难题。我们 把点G称为基点(base 椭圆曲线上简单的加密/解密 • 考虑如下等式: K=k. G [其中 K, G为Ep(a, b)上的点,k为小 于n(n是点G的阶)的整数] 给定k和G,根据加法法则,计算K很容易; 但给定K和G,求k就相对困难了。 这就是椭圆曲线加密算法采用的难题。我们 把点G称为基点(base](https://present5.com/presentation/e51a223f3c3c247cd3b099446024d8d2/image-53.jpg) 椭圆曲线上简单的加密/解密 • 考虑如下等式: K=k. G [其中 K, G为Ep(a, b)上的点,k为小 于n(n是点G的阶)的整数] 给定k和G,根据加法法则,计算K很容易; 但给定K和G,求k就相对困难了。 这就是椭圆曲线加密算法采用的难题。我们 把点G称为基点(base point),k(k
椭圆曲线上简单的加密/解密 • 考虑如下等式: K=k. G [其中 K, G为Ep(a, b)上的点,k为小 于n(n是点G的阶)的整数] 给定k和G,根据加法法则,计算K很容易; 但给定K和G,求k就相对困难了。 这就是椭圆曲线加密算法采用的难题。我们 把点G称为基点(base point),k(k
 现在我们描述一个利用椭圆曲线进行加密通信的过程: 1、用户A选定一条椭圆曲线Ep(a, b),并取椭圆曲线上一点, 作为基点G。 2、用户A选择一个私有密钥k,并生成公开密钥K=k. G。 3、用户A将Ep(a, b)和点K,G传给用户B。 4、用户B接到信息后 ,将待传输的明文编码到Ep(a, b)上一 点M(编码方法很多,这里不作讨论),并产生一个随机 整数r(r
现在我们描述一个利用椭圆曲线进行加密通信的过程: 1、用户A选定一条椭圆曲线Ep(a, b),并取椭圆曲线上一点, 作为基点G。 2、用户A选择一个私有密钥k,并生成公开密钥K=k. G。 3、用户A将Ep(a, b)和点K,G传给用户B。 4、用户B接到信息后 ,将待传输的明文编码到Ep(a, b)上一 点M(编码方法很多,这里不作讨论),并产生一个随机 整数r(r
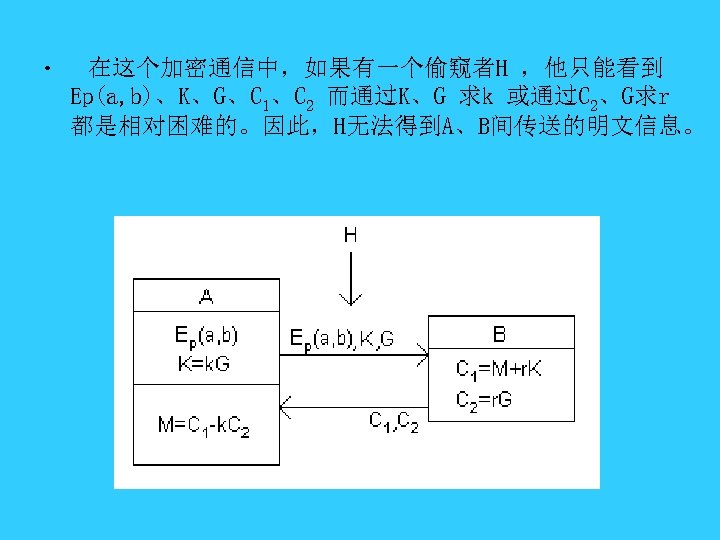 • 在这个加密通信中,如果有一个偷窥者H ,他只能看到 Ep(a, b)、K、G、C 1、C 2 而通过K、G 求k 或通过C 2、G求r 都是相对困难的。因此,H无法得到A、B间传送的明文信息。
• 在这个加密通信中,如果有一个偷窥者H ,他只能看到 Ep(a, b)、K、G、C 1、C 2 而通过K、G 求k 或通过C 2、G求r 都是相对困难的。因此,H无法得到A、B间传送的明文信息。
 密码学中,描述一条Fp上的椭圆曲线,常用到六个参量: T=(p, a, b, G, n, h)。 (p 、a 、b 用来确定一条椭圆曲线, G为基点, n为点G的阶, h 是椭圆曲线上所有点的个数m与n相除的整数部分) 这几个参量取值的选择,直接影响了加密的安全性。参量值一 般要求满足以下几个条件: 1、p 当然越大越安全,但越大,计算速度会变慢,200位左右 可以满足一般安全要求; 2、p≠n×h; 3、pt≠ 1 (mod n),1≤t<20; 4、4 a 3+27 b 2≠ 0 (mod p); 5、n 为素数; 6、h≤ 4。
密码学中,描述一条Fp上的椭圆曲线,常用到六个参量: T=(p, a, b, G, n, h)。 (p 、a 、b 用来确定一条椭圆曲线, G为基点, n为点G的阶, h 是椭圆曲线上所有点的个数m与n相除的整数部分) 这几个参量取值的选择,直接影响了加密的安全性。参量值一 般要求满足以下几个条件: 1、p 当然越大越安全,但越大,计算速度会变慢,200位左右 可以满足一般安全要求; 2、p≠n×h; 3、pt≠ 1 (mod n),1≤t<20; 4、4 a 3+27 b 2≠ 0 (mod p); 5、n 为素数; 6、h≤ 4。
 椭圆曲线下的D-H协议 • can do key exchange analogous to D-H • users select a suitable curve Ep(a, b) • select base point G=(x 1, y 1) with large order n s. t. n. G=O • A & B select private keys n. A
椭圆曲线下的D-H协议 • can do key exchange analogous to D-H • users select a suitable curve Ep(a, b) • select base point G=(x 1, y 1) with large order n s. t. n. G=O • A & B select private keys n. A
 ECC Encryption/Decryption • several alternatives, will consider simplest • must first encode any message M as a point Pm(x, y) on the elliptic curve • select suitable curve & point G as in D-H • each user chooses private key n. A
ECC Encryption/Decryption • several alternatives, will consider simplest • must first encode any message M as a point Pm(x, y) on the elliptic curve • select suitable curve & point G as in D-H • each user chooses private key n. A
 ECC Security • relies on elliptic curve logarithm problem • fastest method is “Pollard rho method” • compared to factoring, can use much smaller key sizes than with RSA etc • for equivalent key lengths computations are roughly equivalent • hence for similar security ECC offers significant computational advantages
ECC Security • relies on elliptic curve logarithm problem • fastest method is “Pollard rho method” • compared to factoring, can use much smaller key sizes than with RSA etc • for equivalent key lengths computations are roughly equivalent • hence for similar security ECC offers significant computational advantages
 软件注册保护应用(1) • 我们知道将公开密钥算法作为软件注册算法的好处是Cracker很难通 过跟踪验证算法得到注册机。下面,将简介一种利用Fp(a, b)椭圆曲 线进行软件注册的方法。 软件作者按如下方法制作注册机(也可称为签名过程) 1、选择一条椭圆曲线Ep(a, b),和基点G; 2、选择私有密钥k(k
软件注册保护应用(1) • 我们知道将公开密钥算法作为软件注册算法的好处是Cracker很难通 过跟踪验证算法得到注册机。下面,将简介一种利用Fp(a, b)椭圆曲 线进行软件注册的方法。 软件作者按如下方法制作注册机(也可称为签名过程) 1、选择一条椭圆曲线Ep(a, b),和基点G; 2、选择私有密钥k(k
 软件注册保护应用(1) • 软件验证过程如下:(软件中存有椭圆曲线Ep(a, b),和基点G,公开 密钥K) 1、从用户输入的序列号中,提取sn以及Hash; 2、计算点R≡sn*G+Hash*K ( mod p ),如果sn、Hash正确,其 值等于软件作者签名过程中点R(x, y)的坐标,因为 sn≡r-Hash*k (mod n) 所以 sn*G + Hash*K =(r-Hash*k)*G+Hash*K =r. G-Hash*k. G+Hash*K =r. G- Hash*K+ Hash*K =r. G=R ; 3、将用户名和点R的坐标值x, y作为参数,计算 H=SHA(username, x, y); 4、如果H=Hash 则注册成功。如果H≠Hash ,则注册失败(为什 么?提示注意点R与Hash的关联性)。
软件注册保护应用(1) • 软件验证过程如下:(软件中存有椭圆曲线Ep(a, b),和基点G,公开 密钥K) 1、从用户输入的序列号中,提取sn以及Hash; 2、计算点R≡sn*G+Hash*K ( mod p ),如果sn、Hash正确,其 值等于软件作者签名过程中点R(x, y)的坐标,因为 sn≡r-Hash*k (mod n) 所以 sn*G + Hash*K =(r-Hash*k)*G+Hash*K =r. G-Hash*k. G+Hash*K =r. G- Hash*K+ Hash*K =r. G=R ; 3、将用户名和点R的坐标值x, y作为参数,计算 H=SHA(username, x, y); 4、如果H=Hash 则注册成功。如果H≠Hash ,则注册失败(为什 么?提示注意点R与Hash的关联性)。
 软件注册保护应用(2) • 软件作者按如下方法制作注册机(也可称为签名过程) 1、选择一条椭圆曲线Ep(a, b),和基点G; 2、选择私有密钥k(k
软件注册保护应用(2) • 软件作者按如下方法制作注册机(也可称为签名过程) 1、选择一条椭圆曲线Ep(a, b),和基点G; 2、选择私有密钥k(k
 软件注册保护应用(2) • 软件验证过程如下:(软件中存有椭圆曲线Ep(a, b),和基点G,公开 密钥K) • 1、从用户输入的序列号中,提取sn以及x’; 2、将用户名作为参数,计算Hash=SHA(username); 3、计算 R=(Hash*G+x’*K)/sn,如果sn、Hash正确, 其值等于 软件作者签名过程中点R(x, y),因为 sn≡(Hash+x’*k)/r (mod n) 所以 (Hash*G+x’*K)/sn =(Hash*G+x’*K)/[(Hash+x’*k)/r] =(Hash*G+x’*K)/[(Hash*G+x’*k*G)/(r. G)] =r. G*[(Hash*G+x’*K)/(Hash*G+x’*K)] =r. G=R (mod p) 4、v≡x (mod n) 5、如果v=x’ 则注册成功。如果v≠x’ ,则注册失败。
软件注册保护应用(2) • 软件验证过程如下:(软件中存有椭圆曲线Ep(a, b),和基点G,公开 密钥K) • 1、从用户输入的序列号中,提取sn以及x’; 2、将用户名作为参数,计算Hash=SHA(username); 3、计算 R=(Hash*G+x’*K)/sn,如果sn、Hash正确, 其值等于 软件作者签名过程中点R(x, y),因为 sn≡(Hash+x’*k)/r (mod n) 所以 (Hash*G+x’*K)/sn =(Hash*G+x’*K)/[(Hash+x’*k)/r] =(Hash*G+x’*K)/[(Hash*G+x’*k*G)/(r. G)] =r. G*[(Hash*G+x’*K)/(Hash*G+x’*K)] =r. G=R (mod p) 4、v≡x (mod n) 5、如果v=x’ 则注册成功。如果v≠x’ ,则注册失败。



