Computer Organization and Design Transistors Logic —

Computer Organization and Design Transistors & Logic - I Montek Singh Wed, Oct 10, 2012 Lecture 10 1

Today’s Topics ã Why go digital? ã Encoding bits using voltages ã Digital design primitives l transistors and gates 2

Where are we in this course? ã Things we know so far: l Computers process information l Information is measured in bits l Data can be represented as groups of bits l Computer instructions are encoded as bits l We, humans, don’t want to deal with bits… Ø so we invent Assembly Language and Compilers ã But, what PROCESSES all these bits? 3

A Substrate for Computation ã We can build devices for processing and representing bits using almost any physical phenomenon l currents l voltages l tiny magnets (nanomagnets) l quantum phenomena (quantum computing) l sequences of DNA (DNA computing) l… Ø any physical phenomenon with at least 2 distinct states, which can be measured and controlled 4

Using Electromagnetic Phenomena ã Things like: l voltages , phase, currents, frequency ã Using voltages to encode information l Voltage pros: Ø easy generation, detection Ø voltage changes can be very fast Ø lots of engineering knowledge already l Voltage cons: Ø easily affected by environment Ø need wires everywhere to transmit 5

Encoding using Voltage (example) ã Representation of each point (x, y) on a B&W pic: l 0 volts: BLACK l 1 volt: WHITE l 0. 37 volts: 37% Gray, etc. ã Representation of a picture: l scan points in some prescribed raster order… l generate voltage waveform How much information at each point? 6

Information Processing = Computation ã First, let’s introduce some processing blocks: (say, using a fancy photocopier/scanner/printer) v Copy v v INV 1 -v 7

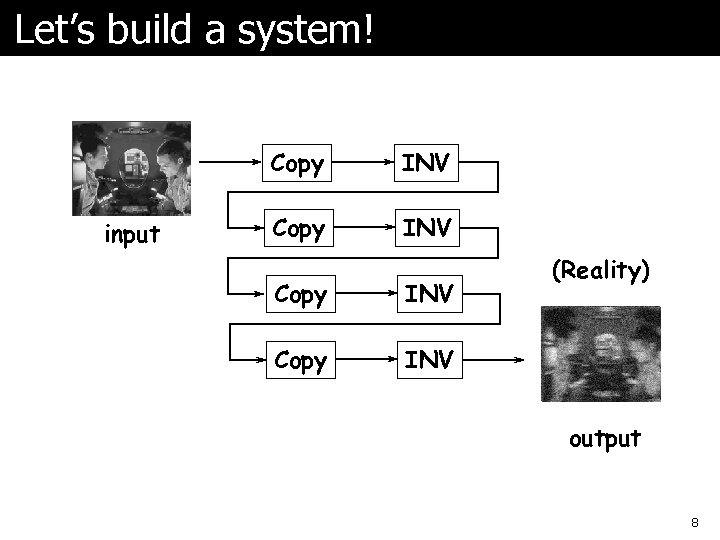Let’s build a system! Copy input INV Copy INV (In Theory) (Reality) ? output 8

Why Did Our System Fail? ã Why doesn’t reality match theory? l COPY Operator doesn’t work right? l INVERSION Operator doesn’t work right? l Theory is imperfect? l Reality is imperfect? l Our system architecture stinks? ã ANSWER: all of the above! l Noise and inaccuracy are inevitable l We cannot reliably reproduce infinite information in the presence of noise Ø consequence of Shannon’s theorem l Must design our system to tolerate some amount of error if it is to process information reliably! 9

The Key to System Design ã A SYSTEM is a structure that is guaranteed to exhibit a specified behavior, assuming all of its components obey their specified behaviors. ã How is this achieved? CONTRACTS! l Every system component will have clear obligations and responsibilities. If these are maintained we have every right to expect the system to behave as planned. If contracts are violated all bets are off. l Much like object-oriented programming! 10

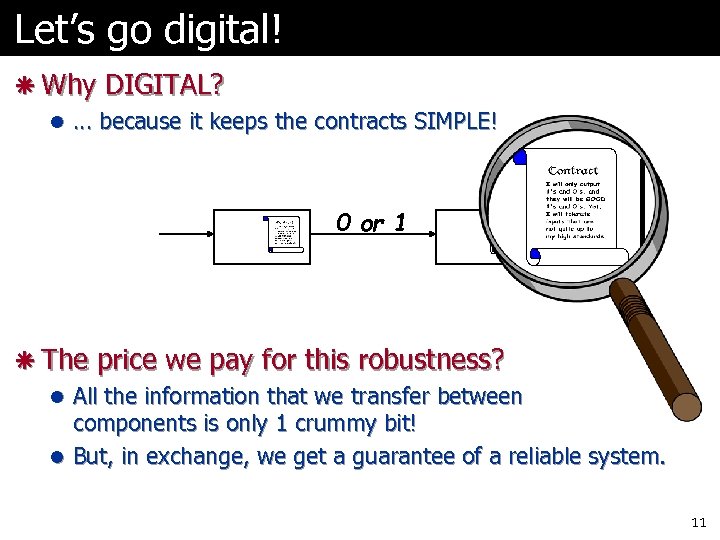Let’s go digital! ã Why DIGITAL? l … because it keeps the contracts SIMPLE! 0 or 1 ã The price we pay for this robustness? l All the information that we transfer between components is only 1 crummy bit! l But, in exchange, we get a guarantee of a reliable system. 11

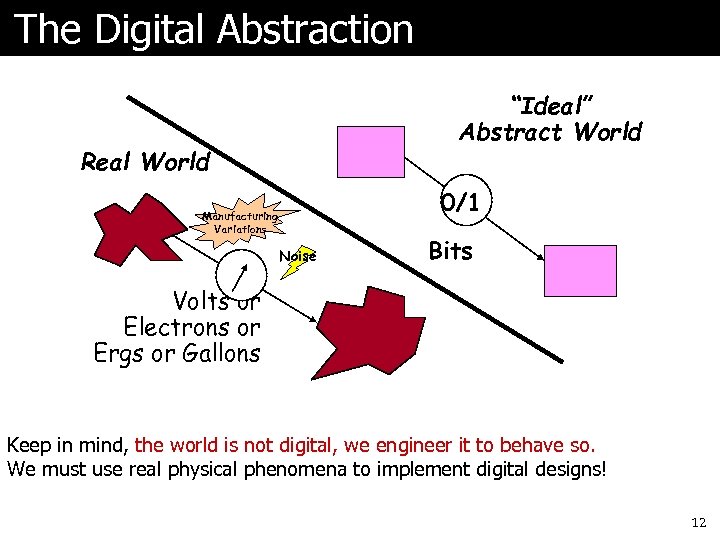The Digital Abstraction “Ideal” Abstract World Real World 0/1 Manufacturing Variations Noise Bits Volts or Electrons or Ergs or Gallons Keep in mind, the world is not digital, we engineer it to behave so. We must use real physical phenomena to implement digital designs! 12

Types of Digital Components ã Two categories of components l those whose output only depends on their current inputs Ø called COMBINATIONAL Ø they are “memory-less”, don’t remember the past l those who output depends also on their past state Ø called SEQUENTIAL Ø they are “state-holding”, remember their past Ø key to building memories 13

Terminology ã System l a reasonably large assembly of components l division of a system into components is typically arbitrary but almost always hierarchical ã Component/Element l an individual part of a bigger system l clearly-defined function and interface l implement it and put a black-box around it l larger components created using smaller components ã Circuit l a small (often leaf-level) component consisting of a network of gates 14

Combinational Components ã A circuit is combinational if-and-only-if it has: l one or more digital inputs l one or more digital outputs l a functional specification that details the value of each output for every possible combination of valid input values Ø output depends only on the latest inputs timing specification consisting (at minimum) of an upper bound tpd on the time this circuit will take to produce the la output value once stable valid input values are applied input A input B input C Output a “ 1” if at least 2 out of 3 of my inputs are a “ 1”. Otherwise, output “ 0”. I will generate a valid output in no more than 2 minutes after seeing valid inputs output Y 15

A Combinational Digital System ã Theorem: A system of interconnected elements is combinational if-and-only-if: l each primitive circuit element is combinational l every input is connected to exactly one output or directly to a source of 0’s or 1’s l the circuit contains no directed cycles Ø no feedback (yet!) ã Proof: By induction l Start with the rightmost level of elements Ø their output only depends on their inputs, which in turn are outputs of the level of element just to their left Ø and so on… until you arrive at the leftmost inputs ã But, in order to realize digital processing elements we have one more requirement! 16

Noise Margins ã Key idea: Keep “ 0”s distinct from the “ 1”s l say, “ 0” is represented by min voltage (e. g. , 0 volts) l… “ 1” is represented by high voltage (e. g. , 1. 8 volts) l use the same voltage representation throughout the entire system! ã For reliability, outlaw “close calls” l forbid a range of voltages between “ 0” and “ 1” Valid “ 0” Min Voltage Invalid Forbidden Zone Valid “ 1” volts Max Voltage CONSEQUENCE: Notion of “VALID” and “INVALID” logic levels 17

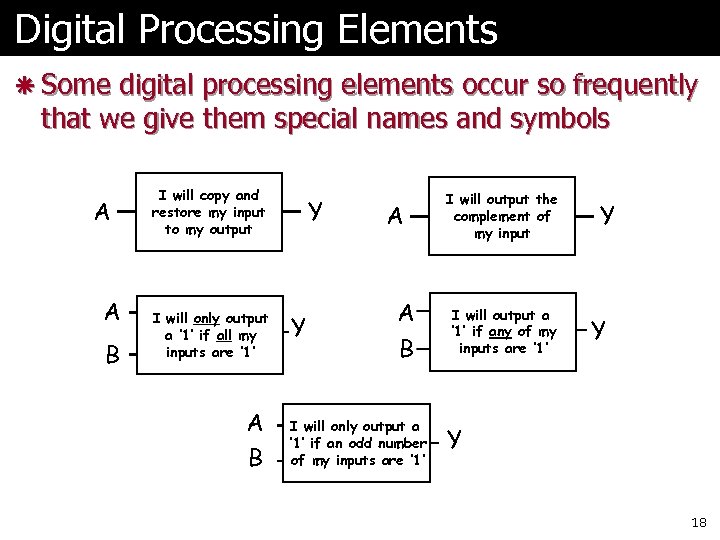Digital Processing Elements ã Some digital processing elements occur so frequently that we give them special names and symbols A A B I will copy and restore my input to my output buffer I will only output a ‘ 1’ if all my AND inputs are ‘ 1’ A B Y Y A A B I will only output a ‘ 1’ if an XOR odd number of my inputs are ‘ 1’ I will output the complement of my input inverter I will output a ‘ 1’ if any of my OR inputs are ‘ 1’ Y Y Y 18

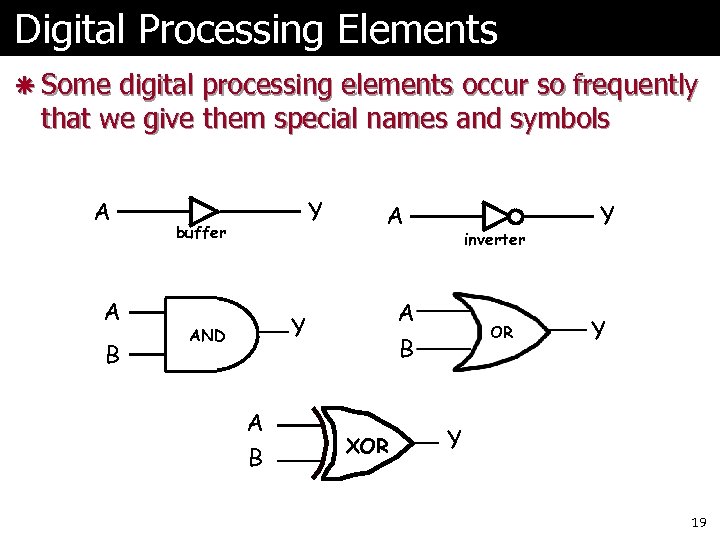Digital Processing Elements ã Some digital processing elements occur so frequently that we give them special names and symbols A A B Y buffer A A B Y AND A B inverter XOR OR Y Y Y 19

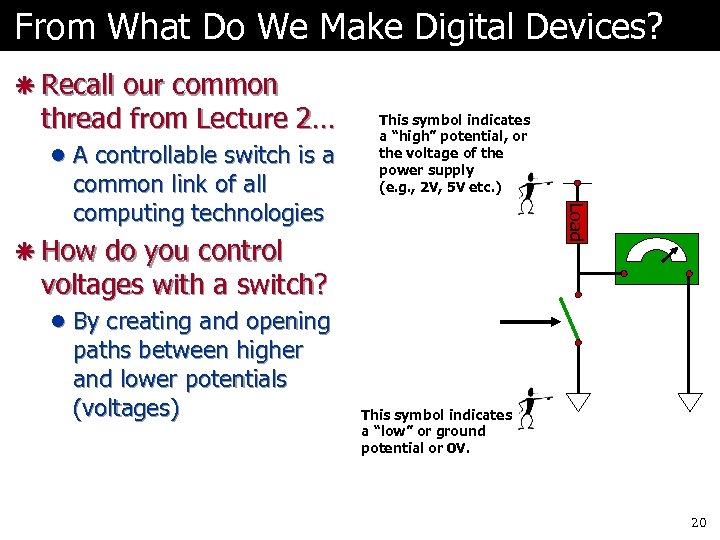From What Do We Make Digital Devices? ã Recall our common thread from Lecture 2… l A controllable switch is a Load common link of all computing technologies This symbol indicates a “high” potential, or the voltage of the power supply (e. g. , 2 V, 5 V etc. ) ã How do you control voltages with a switch? l By creating and opening paths between higher and lower potentials (voltages) This symbol indicates a “low” or ground potential or 0 V. 20

Most common technology today ã … is called CMOS l everything built using transistors l a transistor is just a switch ã 2 types of transistors l n-type Ø called “NFET”, or “n. MOS” or “n channel transistor” or “n transistor” Ø switch is on (i. e. , conducts) when its control input is ‘ 1’ l p-type Ø called “PFET”, or “p. MOS”, or “p channel transistor” or “p transistor” Ø switch is on (i. e. , conducts) when its control input is ‘ 0’ l need both types to build useful gates 21

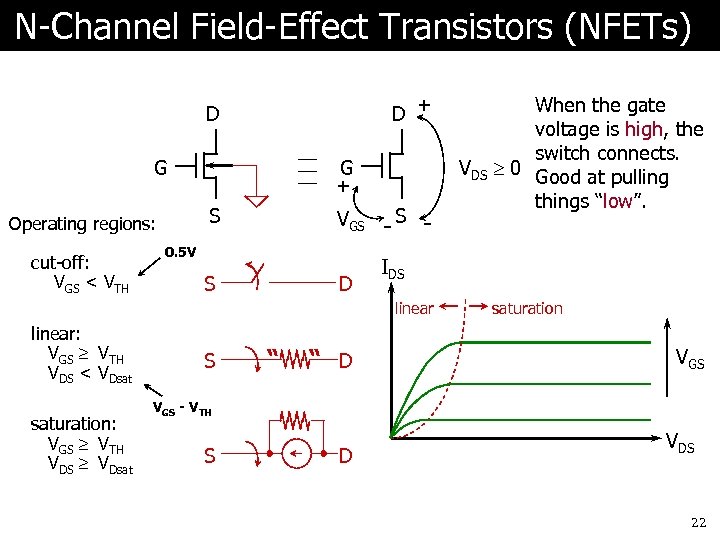N-Channel Field-Effect Transistors (NFETs) D + D G S Operating regions: cut-off: VGS < VTH VDS G + VGS 0. 5 V S D - S - IDS linear: VGS ³ VTH VDS < VDsat saturation: VGS ³ VTH VDS ³ VDsat S “ “ D When the gate voltage is high, the switch connects. ³ 0 Good at pulling things “low”. saturation VGS - VTH S D VDS 22

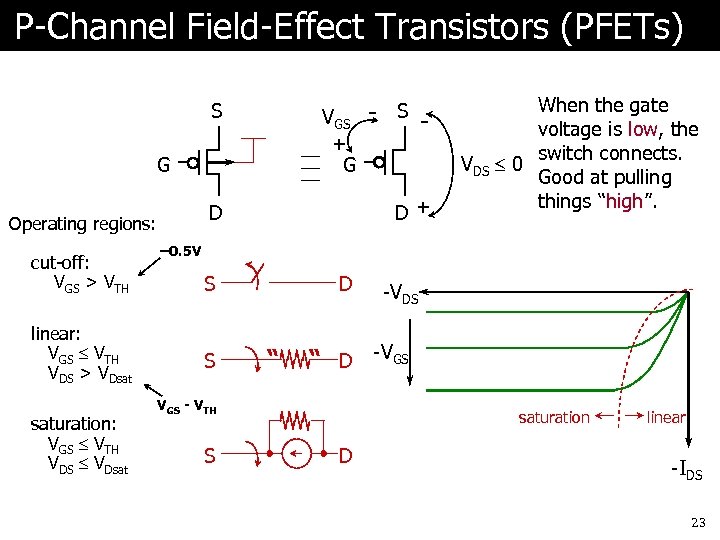P-Channel Field-Effect Transistors (PFETs) S VGS + G G cut-off: VGS > VTH linear: VGS VTH VDS > VDsat saturation: VGS VTH VDS VDsat VDS D+ D Operating regions: - S - When the gate voltage is low, the switch connects. 0 Good at pulling things “high”. – 0. 5 V S S D “ “ D -VGS - VTH S -VDS saturation D linear -IDS 23

Next time ã Build gates using transistors ã Build larger circuits using gates 24