Computer Image Vision Processing Introduction to Image Processing

Computer Image Vision Processing Introduction to Image Processing Cameras, lenses and sensors Cosimo Distante Cosimo. distante@cnr. it Cosimo. distante@unisalento. it

Image Processing Cameras, lenses and sensors • Camera Models – Pinhole Perspective Projection • Camera with Lenses • Sensing • The Human Eye

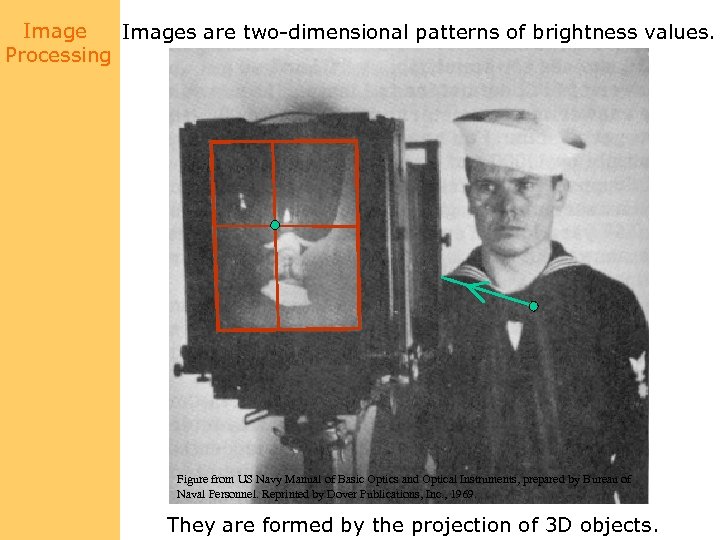Images are two-dimensional patterns of brightness values. Processing Figure from US Navy Manual of Basic Optics and Optical Instruments, prepared by Bureau of Naval Personnel. Reprinted by Dover Publications, Inc. , 1969. They are formed by the projection of 3 D objects.

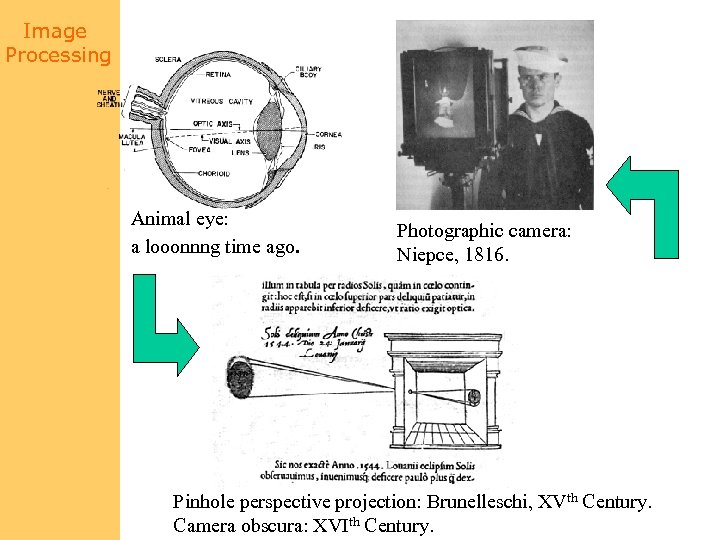Image Processing Animal eye: a looonnng time ago. Photographic camera: Niepce, 1816. Pinhole perspective projection: Brunelleschi, XVth Century. Camera obscura: XVIth Century.

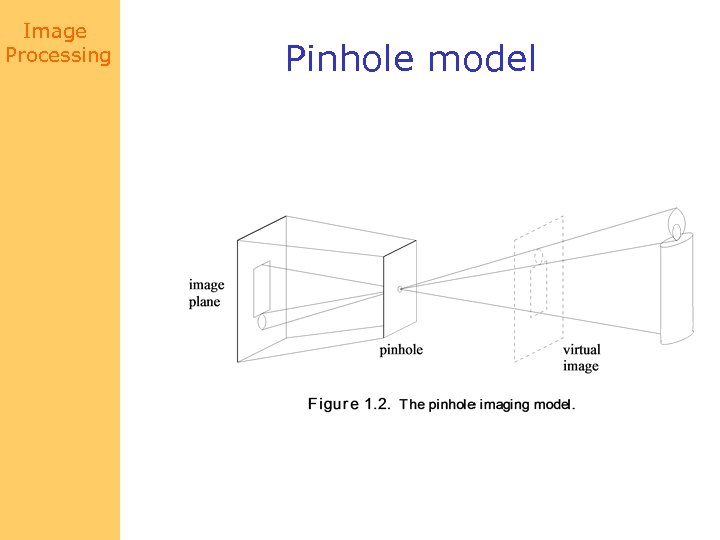Image Processing Pinhole model

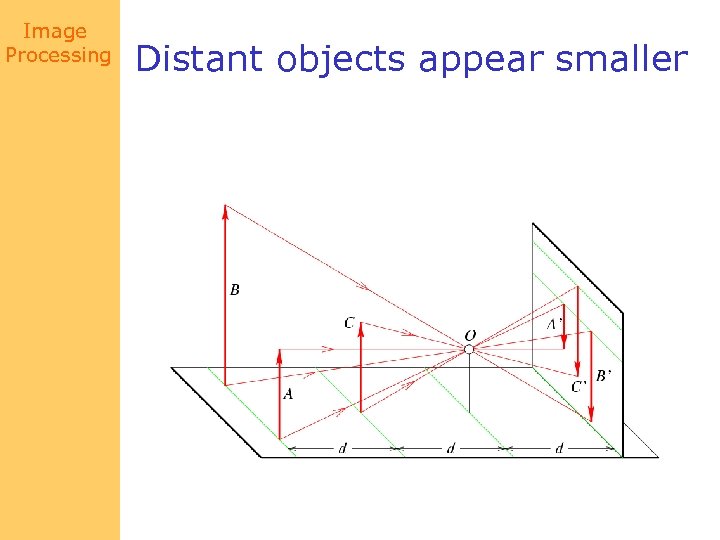Image Processing Distant objects appear smaller

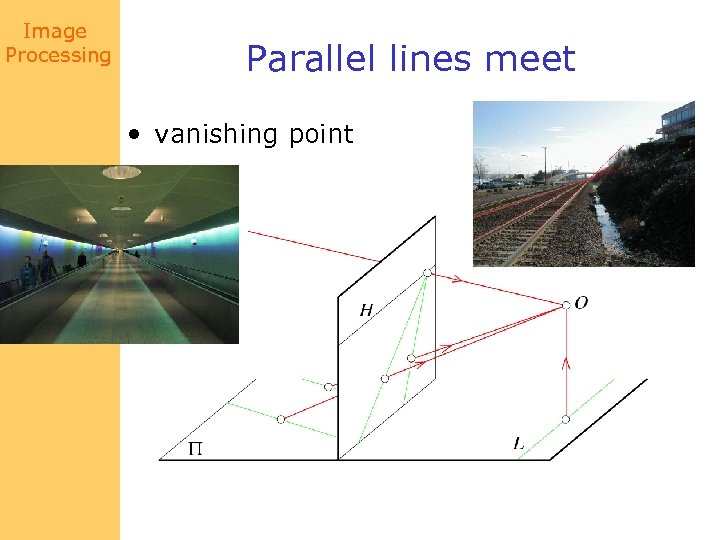Image Processing Parallel lines meet • vanishing point

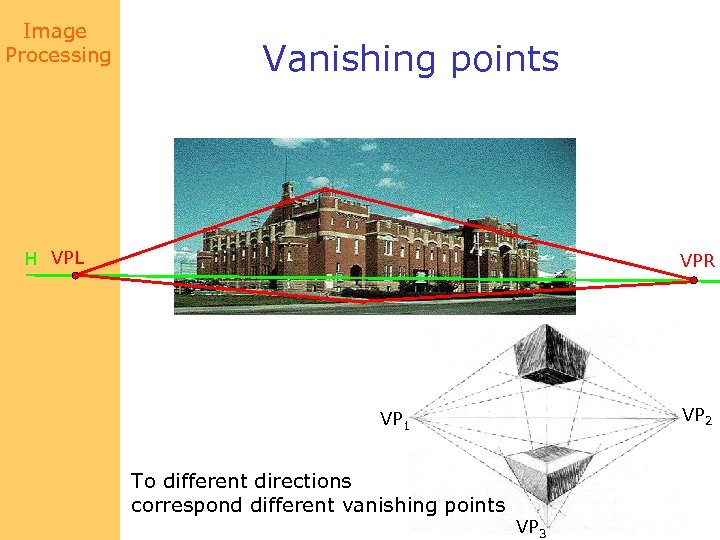Image Processing Vanishing points H VPL VPR VP 2 VP 1 To different directions correspond different vanishing points VP 3

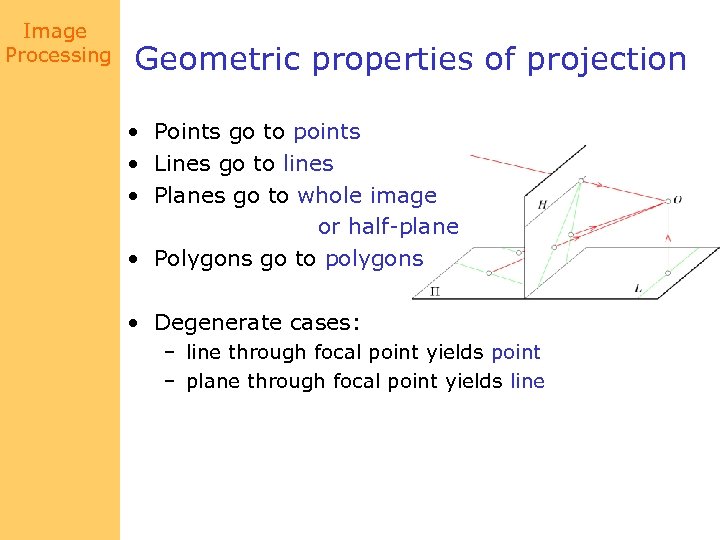Image Processing Geometric properties of projection • Points go to points • Lines go to lines • Planes go to whole image or half-plane • Polygons go to polygons • Degenerate cases: – line through focal point yields point – plane through focal point yields line

Image Processing Pinhole Camera Model X Image plane P=(X, Z) P=(x, f) x Optical axis O f Z X

Image Processing Pinhole Camera Model Y Image plane P=(Y, Z) P=(y, f) y Optical axis O f Z Y

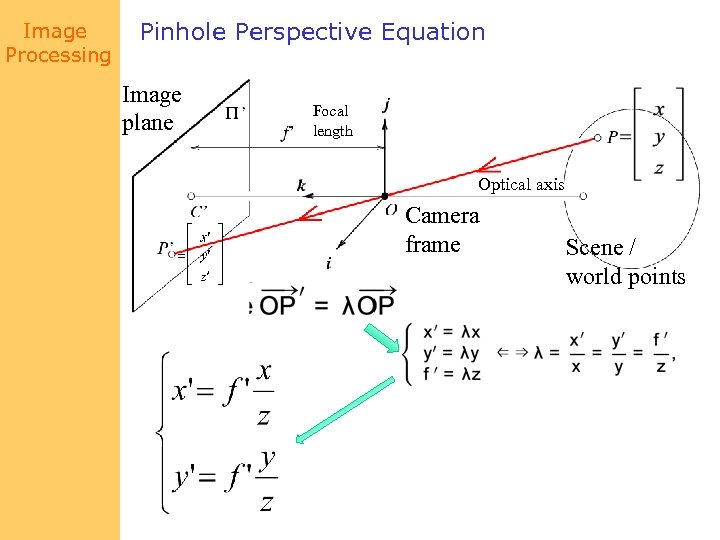Image Processing Pinhole Perspective Equation Image plane Focal length Optical axis Camera frame Scene / world points

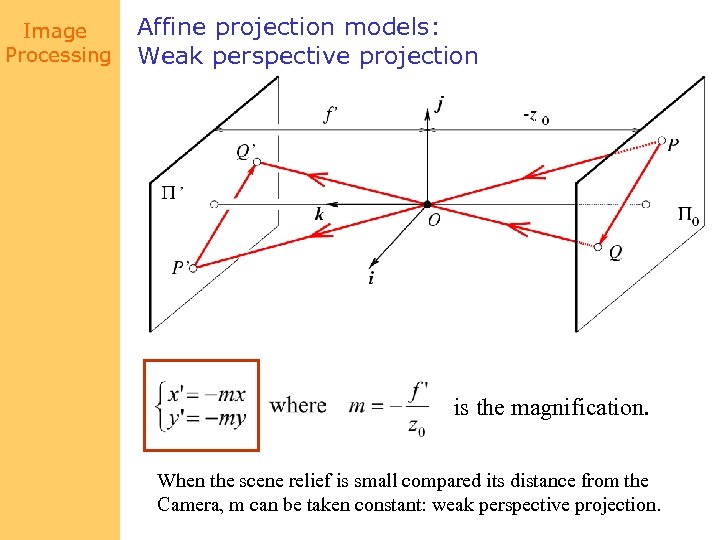Image Processing Affine projection models: Weak perspective projection is the magnification. When the scene relief is small compared its distance from the Camera, m can be taken constant: weak perspective projection.

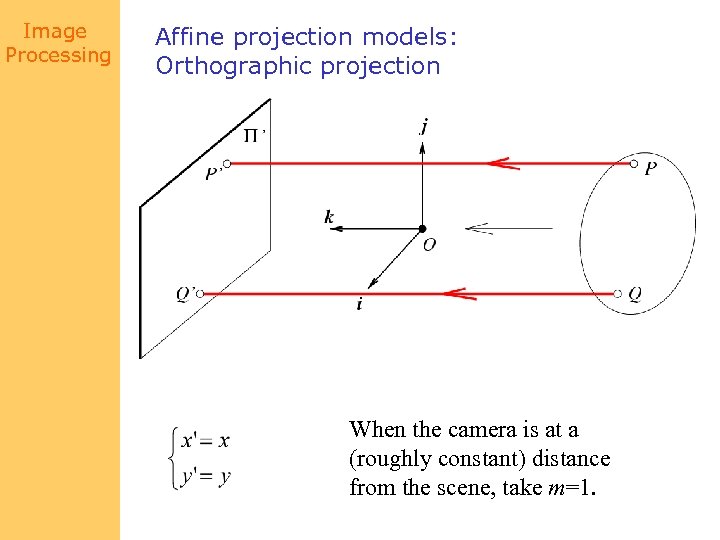Image Processing Affine projection models: Orthographic projection When the camera is at a (roughly constant) distance from the scene, take m=1.

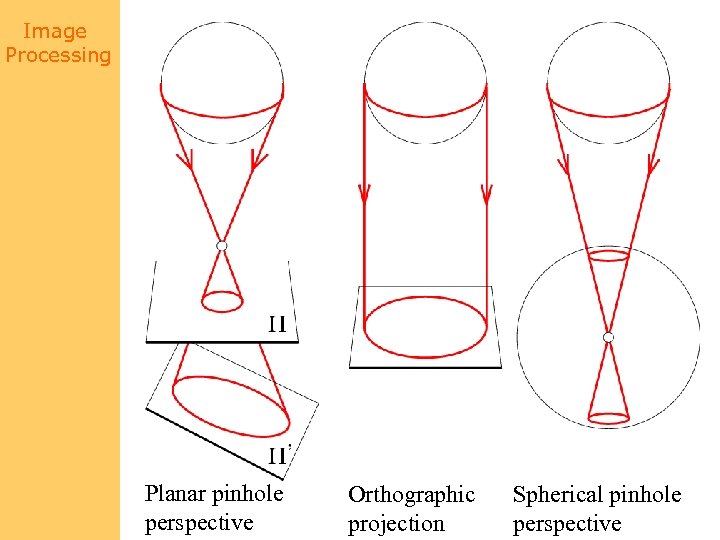Image Processing Planar pinhole perspective Orthographic projection Spherical pinhole perspective

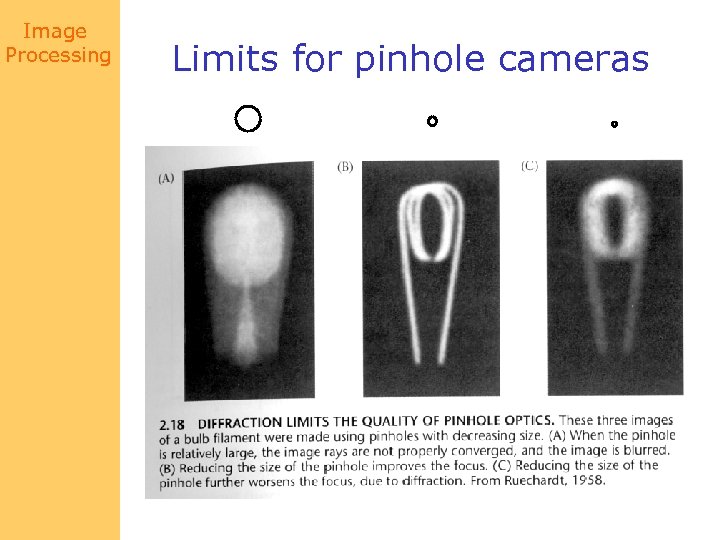Image Processing Limits for pinhole cameras

Image Processing Limits for pinhole cameras

Image Processing Camera obscura + lens

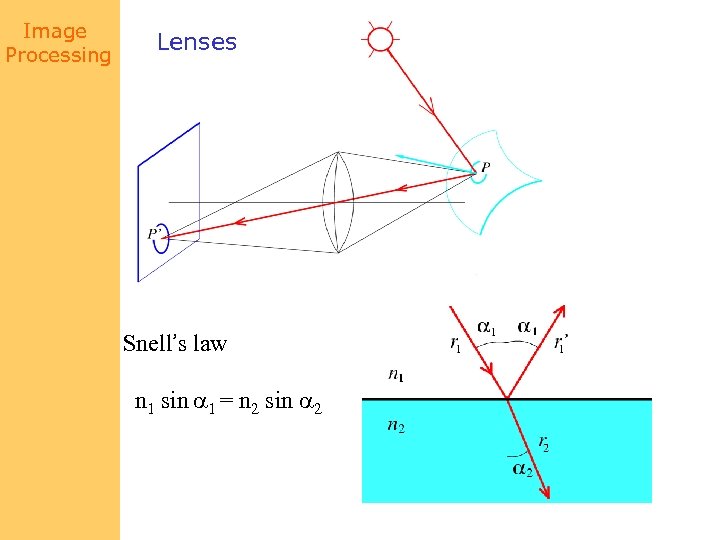Image Processing Lenses Snell’s law n 1 sin a 1 = n 2 sin a 2 Descartes’ law

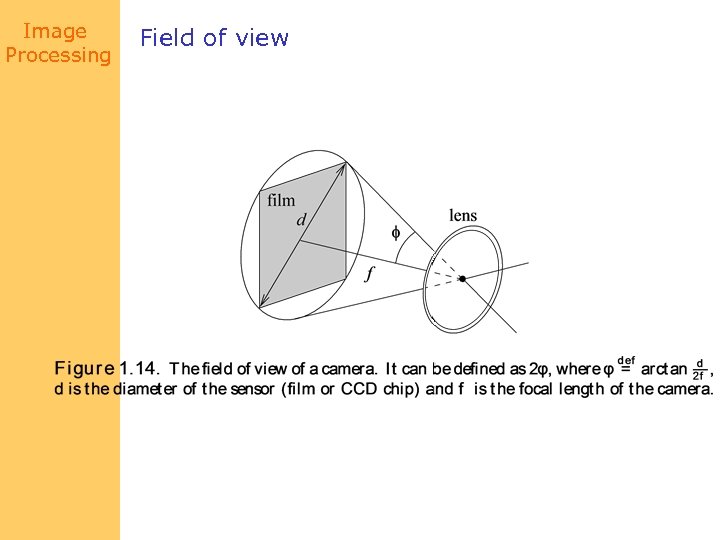Image Processing Field of view

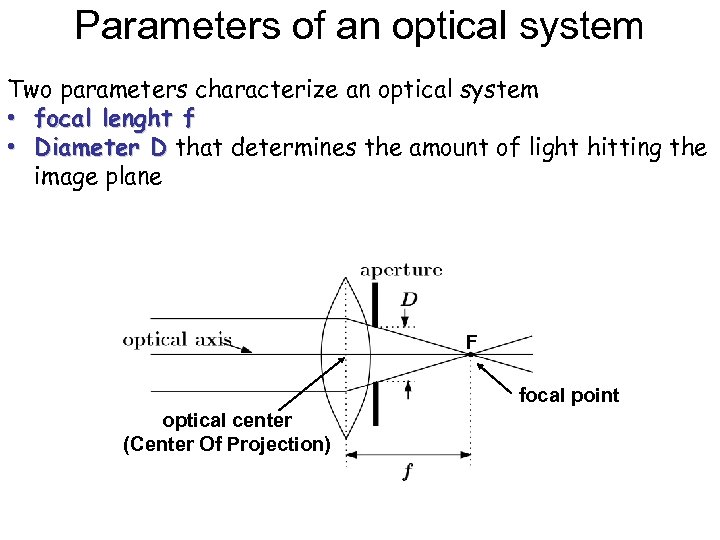Parameters of an optical system Two parameters characterize an optical system • focal lenght f • Diameter D that determines the amount of light hitting the image plane F focal point optical center (Center Of Projection)

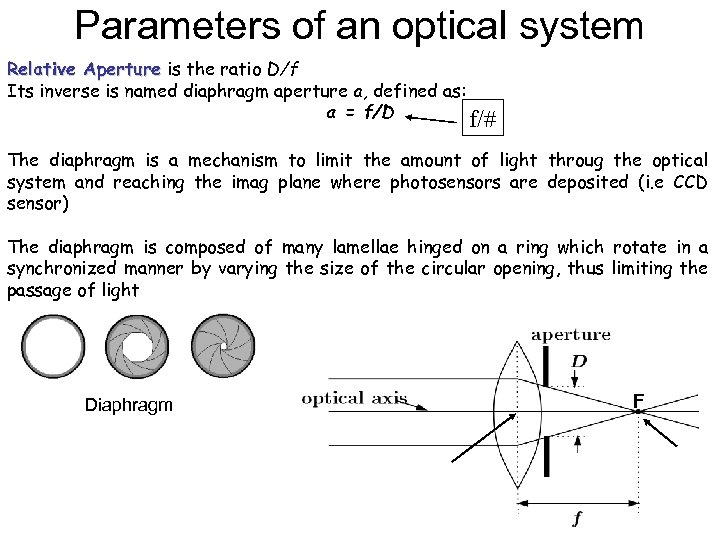Parameters of an optical system Relative Aperture is the ratio D/f Its inverse is named diaphragm aperture a, defined as: a = f/D f/# The diaphragm is a mechanism to limit the amount of light throug the optical system and reaching the imag plane where photosensors are deposited (i. e CCD sensor) The diaphragm is composed of many lamellae hinged on a ring which rotate in a synchronized manner by varying the size of the circular opening, thus limiting the passage of light Diaphragm F

Parameters of an optical system Aperture scale varies with square of first value is 1 Other values are 1. 4, 2, 2. 8, 4, 5. 6, 8, 11, 16, 32, 45, 60, … Normally an optical system is dinamically configured to project the right amount of light, by compensating with the exposure time

Parameters of an optical system 35 mm set at f/11, Aperture varies from f/2. 0 to f/22

Parameters of an optical system

Lens field of view computation Lens choise depend on the wanted acquired scene. Per le telecamere con CCD 1/4” Focal lenght (mm) = Target distance (m. ) x 3, 6 : width (m. ) Per tutte le altre telecamere con CCD 1/3" Focal lenght (mm) = Target distance (m. ) x 4, 8 : width (m. )

Focus and depth of field f / 5. 6 f / 32 Changing the aperture size affects depth of field • A smaller aperture increases the range in which the object is approximately in focus Flower images from Wikipedia http: //en. wikipedia. org/wiki/Depth_of_field

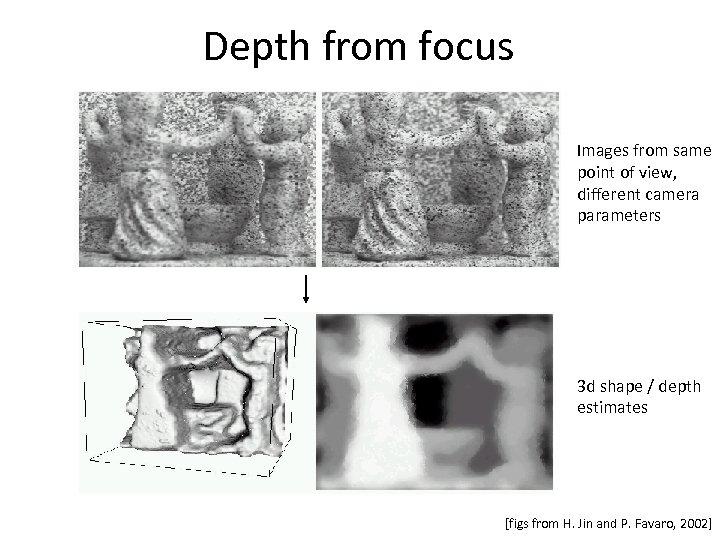Depth from focus Images from same point of view, different camera parameters 3 d shape / depth estimates [figs from H. Jin and P. Favaro, 2002]

Field of view • Angular measure of portion of 3 d space seen by the camera Images from http: //en. wikipedia. org/wiki/Angle_of_view K. Grauman

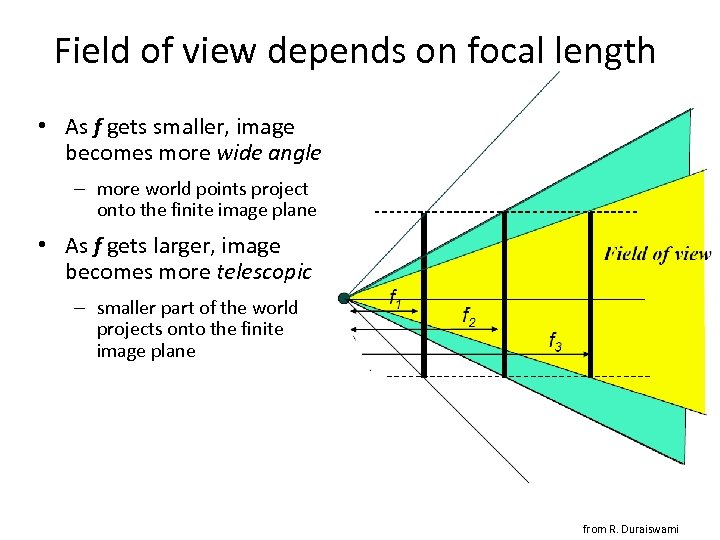Field of view depends on focal length • As f gets smaller, image becomes more wide angle – more world points project onto the finite image plane • As f gets larger, image becomes more telescopic – smaller part of the world projects onto the finite image plane from R. Duraiswami

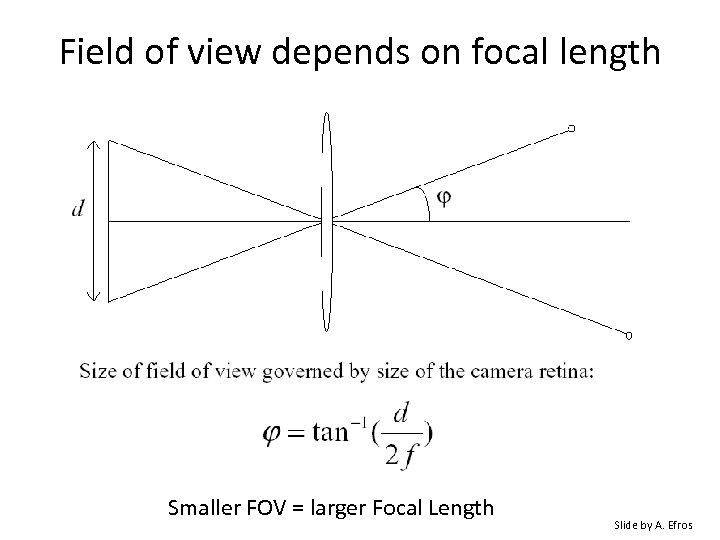Field of view depends on focal length Smaller FOV = larger Focal Length Slide by A. Efros

Vignetting http: //www. ptgui. com/examples/vigntutorial. html http: //www. tlucretius. net/Photo/e. Holga. html

Vignetting • “natural”: • “mechanical”: intrusion on optical path

Chromatic aberration

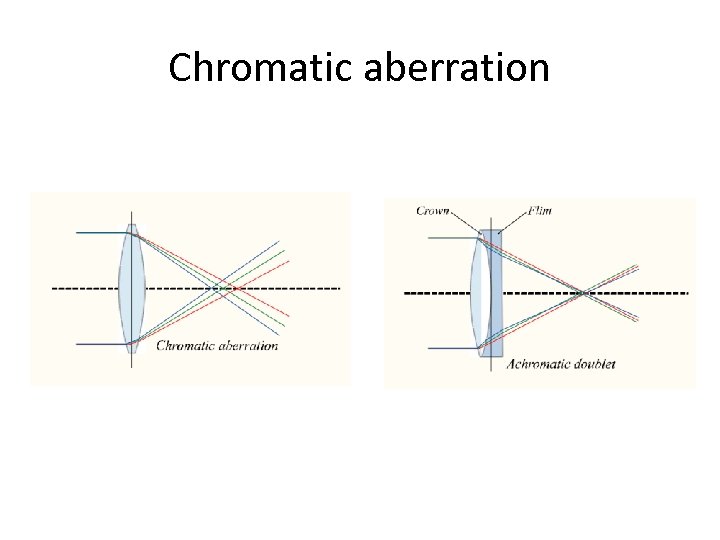Chromatic aberration

Image Processing Deviations from the lens model 3 assumptions : 1. all rays from a point are focused onto 1 image point 2. all image points in a single plane 3. magnification is constant deviations from this ideal are aberrations

Image Processing Aberrations 2 types : 1. geometrical 2. chromatic geometrical : small for paraxial rays study through 3 rd order optics chromatic : refractive index function of wavelength

Image Processing Geometrical aberrations q spherical aberration q astigmatism q distortion q coma aberrations are reduced by combining lenses

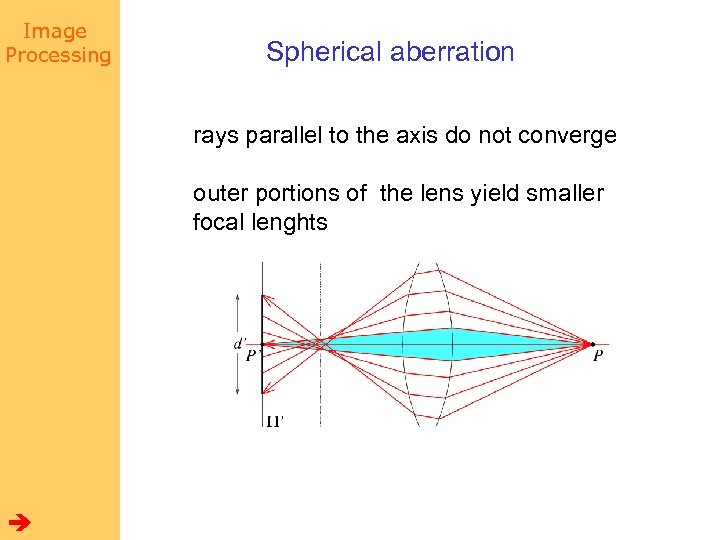Image Processing Spherical aberration rays parallel to the axis do not converge outer portions of the lens yield smaller focal lenghts

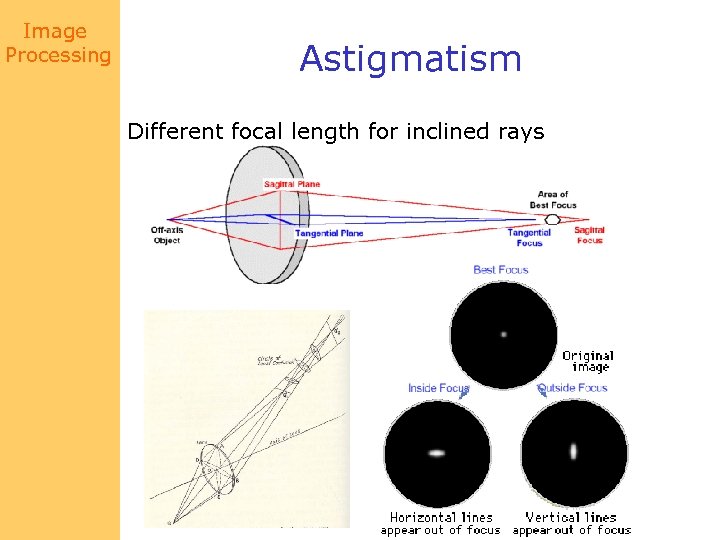Image Processing Astigmatism Different focal length for inclined rays

Image Processing Distortion magnification/focal length different for different angles of inclination pincushion (tele-photo) barrel (wide-angle) Can be corrected! (if parameters are know)

Image Processing Coma point off the axis depicted as comet shaped blob

Image Processing Chromatic aberration rays of different wavelengths focused in different planes cannot be removed completely sometimes achromatization is achieved for more than 2 wavelengths

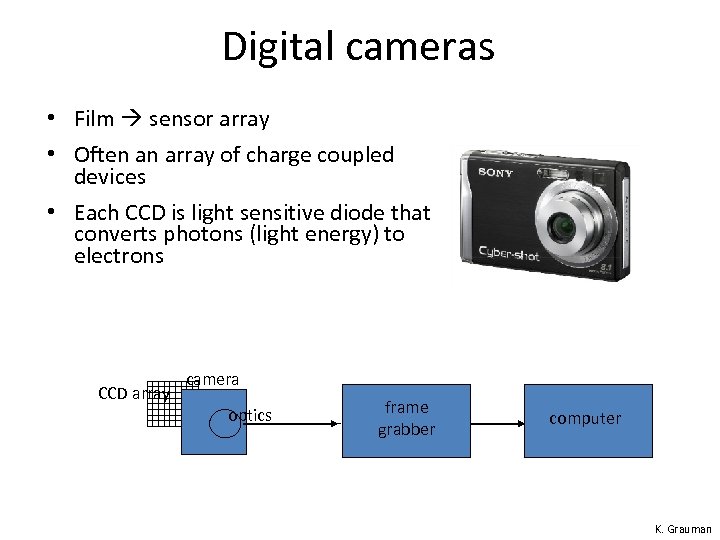Digital cameras • Film sensor array • Often an array of charge coupled devices • Each CCD is light sensitive diode that converts photons (light energy) to electrons CCD array camera optics frame grabber computer K. Grauman

• Historical context Pinhole model: Mozi (470 -390 BCE), Aristotle (384 -322 BCE) • Principles of optics (including lenses): Alhacen (965 -1039 CE) • Camera obscura: Leonardo da Vinci (1452 -1519), Johann Zahn (1631 -1707) • • First photo: Joseph Nicephore Niepce (1822) Daguerréotypes (1839) Photographic film (Eastman, 1889) Cinema (Lumière Brothers, 1895) Color Photography (Lumière Brothers, 1908) Television (Baird, Farnsworth, Zworykin, 1920 s) First consumer camera with CCD: Sony Mavica (1981) • First fully digital camera: Kodak DCS 100 (1990) Slide credit: L. Lazebnik Alhacen’s notes Niepce, “La Table Servie, ” 1822 CCD chip K. Grauman

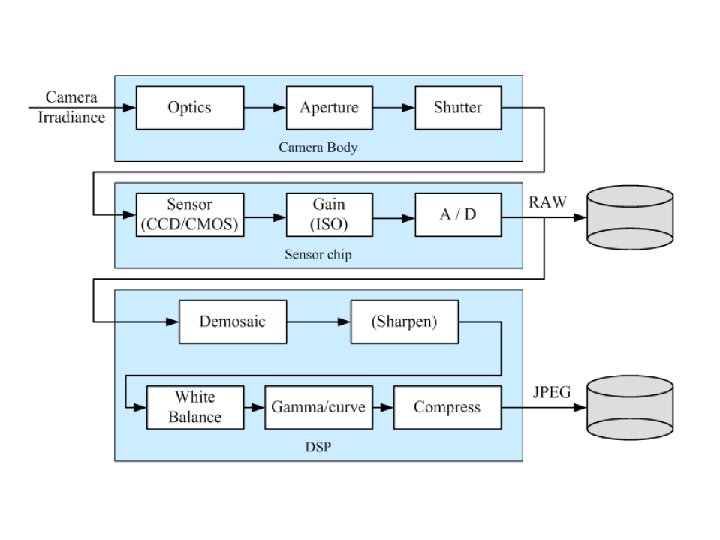
Digital Sensors

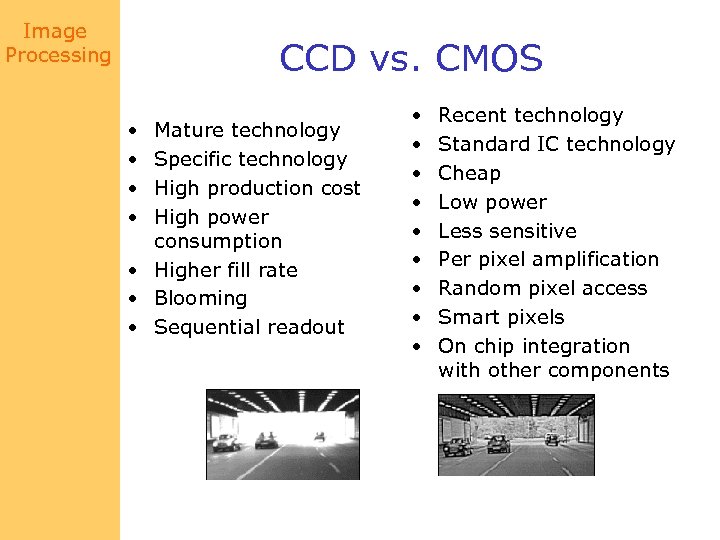Image Processing CCD vs. CMOS • • Mature technology Specific technology High production cost High power consumption • Higher fill rate • Blooming • Sequential readout • • • Recent technology Standard IC technology Cheap Low power Less sensitive Per pixel amplification Random pixel access Smart pixels On chip integration with other components

Resolution • sensor: size of real world scene element a that images to a single pixel • image: number of pixels • Influences what analysis is feasible, affects best representation choice. [fig from Mori et al]

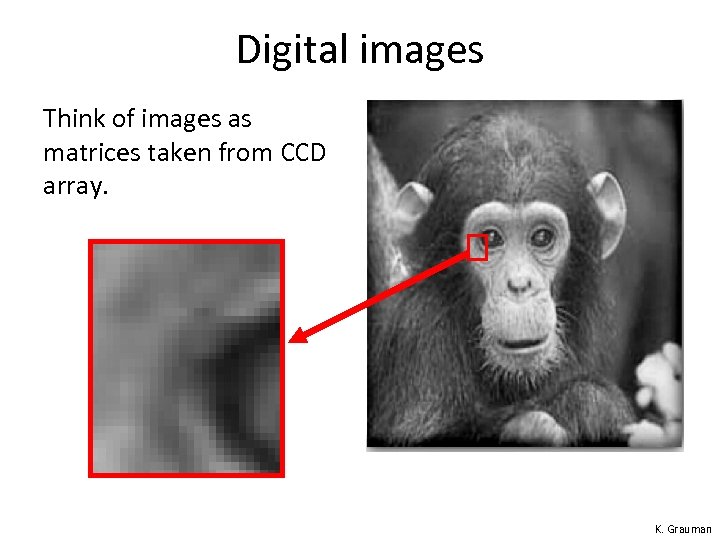Digital images Think of images as matrices taken from CCD array. K. Grauman

Digital images j=1 width 520 i=1 Intensity : [0, 255] 500 height im[176][201] has value 164 im[194][203] has value 37 K. Grauman

Color sensing in digital cameras Bayer grid Estimate missing components from neighboring values (demosaicing) Source: Steve Seitz

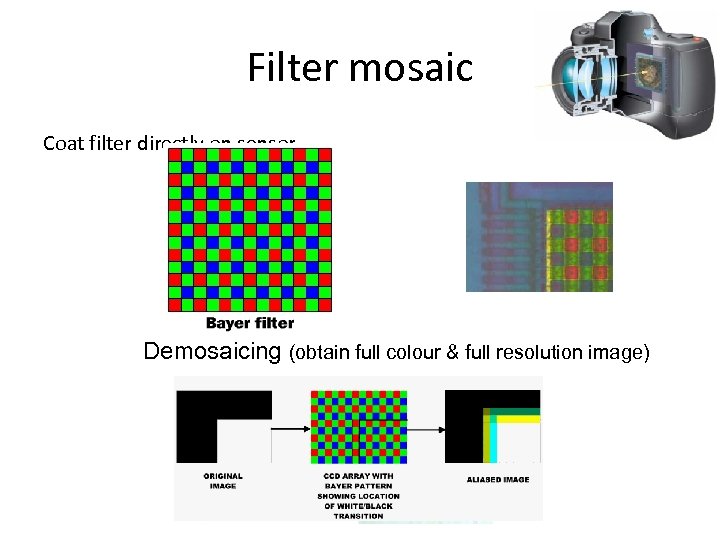Filter mosaic Coat filter directly on sensor Demosaicing (obtain full colour & full resolution image)

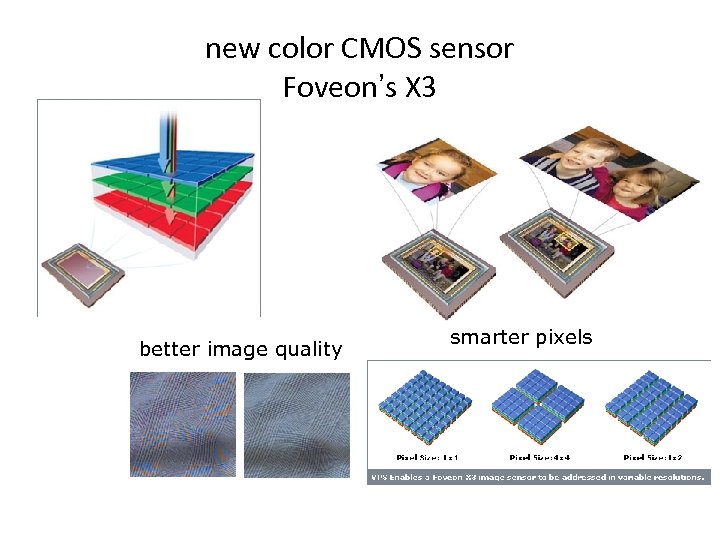new color CMOS sensor Foveon’s X 3 better image quality smarter pixels

Color images, RGB color space R G Much more on color in next lecture… B K. Grauman

Issues with digital cameras Noise – big difference between consumer vs. SLR-style cameras – low light is where you most notice noise Compression – creates artifacts except in uncompressed formats (tiff, raw) Color – color fringing artifacts from Bayer patterns Blooming – charge overflowing into neighboring pixels In-camera processing – oversharpening can produce halos Interlaced vs. progressive scan video – even/odd rows from different exposures Are more megapixels better? – requires higher quality lens – noise issues Stabilization – compensate for camera shake (mechanical vs. electronic) More info online, e. g. , • http: //electronics. howstuffworks. com/digital-camera. htm • http: //www. dpreview. com/

Image Processing Other Cameras: Line Scan Cameras Line scanner • The active element is 1 -dimensional • Usually employed for inspection • They require to have very intense light due to small integration time (from 100 msec to 1 msec)

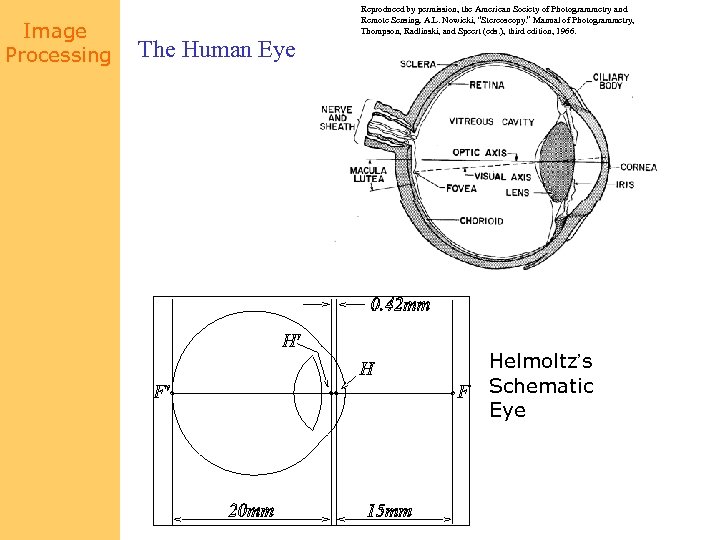Image Processing The Human Eye Reproduced by permission, the American Society of Photogrammetry and Remote Sensing. A. L. Nowicki, “Stereoscopy. ” Manual of Photogrammetry, Thompson, Radlinski, and Speert (eds. ), third edition, 1966. Helmoltz’s Schematic Eye

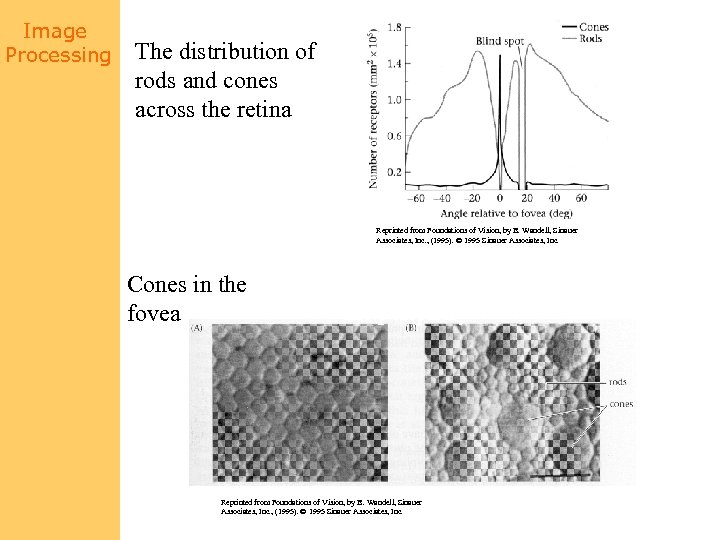Image Processing The distribution of rods and cones across the retina Reprinted from Foundations of Vision, by B. Wandell, Sinauer Associates, Inc. , (1995). 1995 Sinauer Associates, Inc. Cones in the fovea Rods and cones in the periphery Reprinted from Foundations of Vision, by B. Wandell, Sinauer Associates, Inc. , (1995). 1995 Sinauer Associates, Inc.