Computer Graphics Transformations 2 of 25 Types

Computer Graphics Transformations

2 of 25 Types of Transformations – Geometric Transformations • Translation • Rotation • scaling • Linear (preserves parallel lines) • Non-uniform scales, shears or skews – Projection (preserves lines) • Perspective projection • Parallel projection – Non-linear (lines become curves) • Twists, bends, warps, morphs, 2

2 D Transforms • What am I talking about when I say (x’, y’) “transforms”? • Translation (x, y) • Scaling • Rotation

Images taken from Hearn & Baker, “Computer Graphics with Open. GL” (2004) Why Transformations? In graphics, once we have an object described, transformations are used to move that object, scale it and rotate it

Translation Simply moves an object from one position to another xnew = xold + dx y ynew = yold + dy 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 10 Note: House shifts position relative to origin x

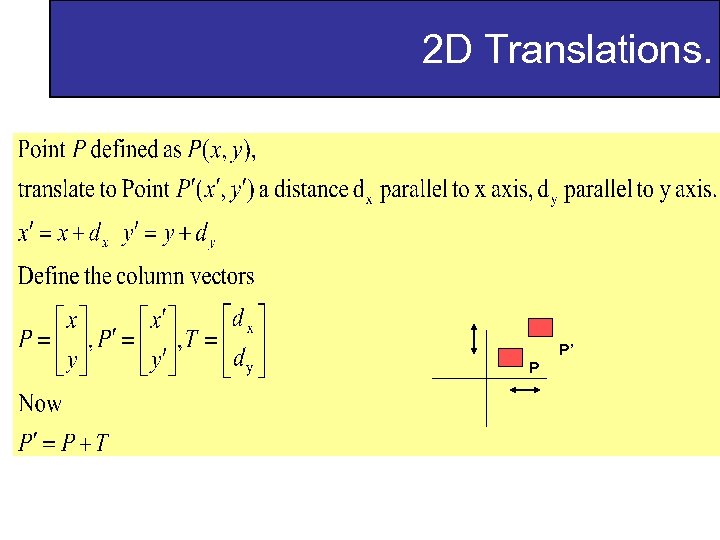2 D Translations. P’ P

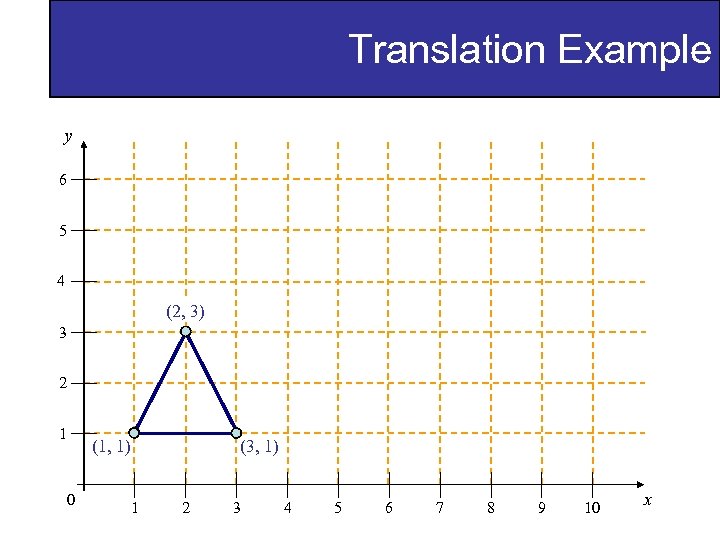Translation Example y 6 5 4 (2, 3) 3 2 1 (1, 1) 0 (3, 1) 1 2 3 4 5 6 7 8 9 10 x

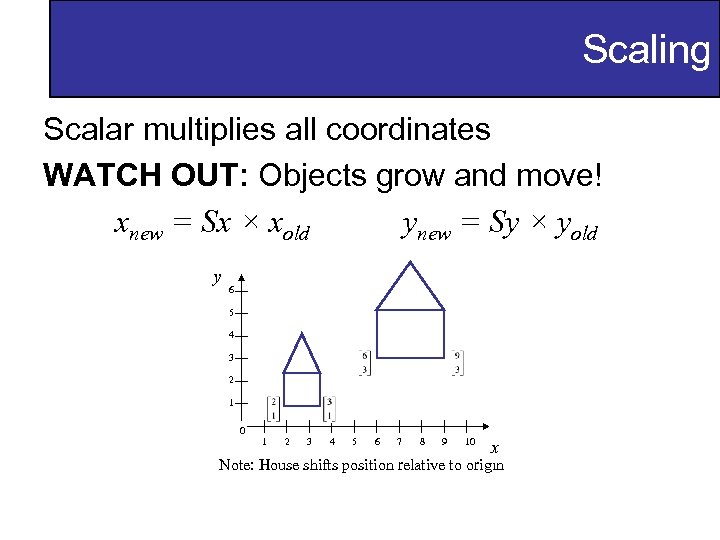Scaling Scalar multiplies all coordinates WATCH OUT: Objects grow and move! xnew = Sx × xold ynew = Sy × yold y 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 10 x Note: House shifts position relative to origin

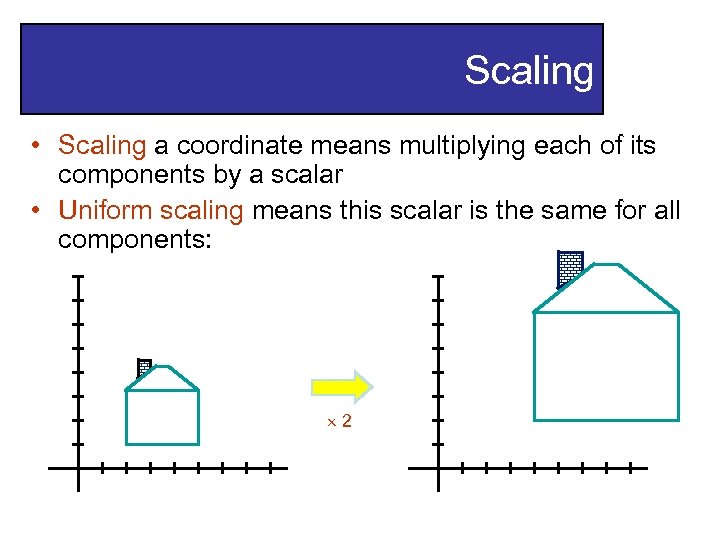Scaling • Scaling a coordinate means multiplying each of its components by a scalar • Uniform scaling means this scalar is the same for all components: 2

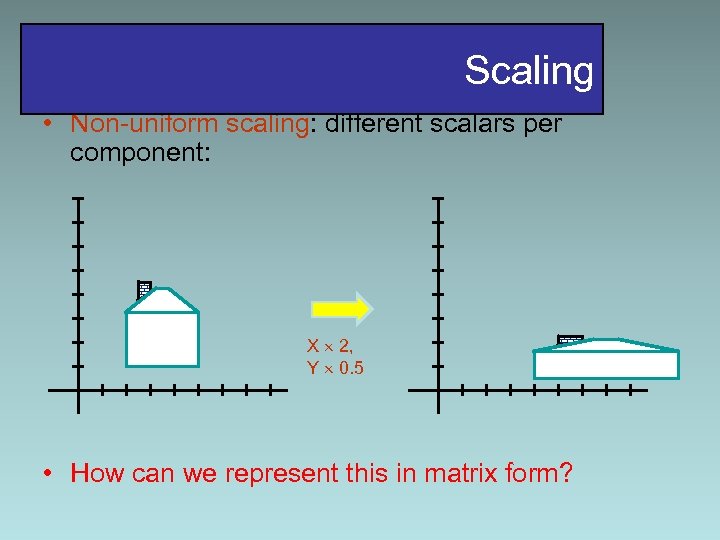Scaling • Non-uniform scaling: different scalars per component: X 2, Y 0. 5 • How can we represent this in matrix form?

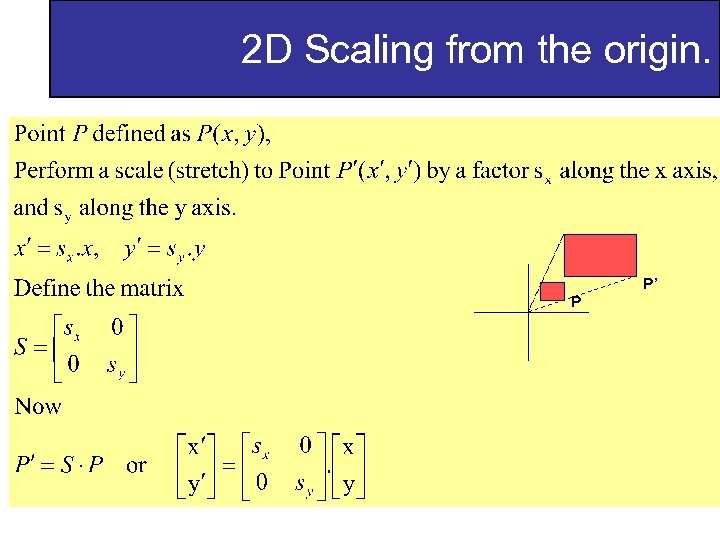2 D Scaling from the origin. P’ P

Scaling Example y 6 5 4 (2, 3) 3 2 1 (1, 1) 0 1 (3, 1) 2 3 4 5 6 7 8 9 10

Rotation Rotates all coordinates by a specified angle xnew = xold × cosθ – yold × sinθ ynew = xold × sinθ + yold × cosθ Points are always rotated about the origin y 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 10 x

14 of 25 2 D Rotation about the origin. Rewriting in matrix form gives us :

2 D Rotation about the origin. y P’(x’, y’) P(x, y) r y r x x

2 D Rotation about the origin. y P’(x’, y’) P(x, y) r y r x x

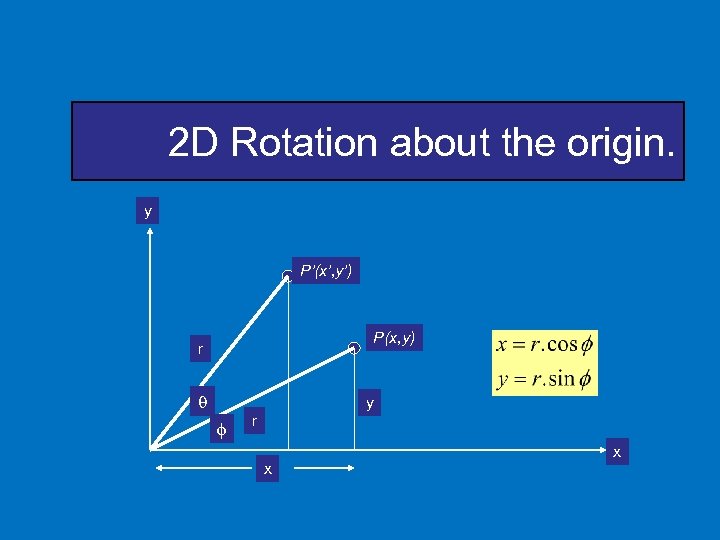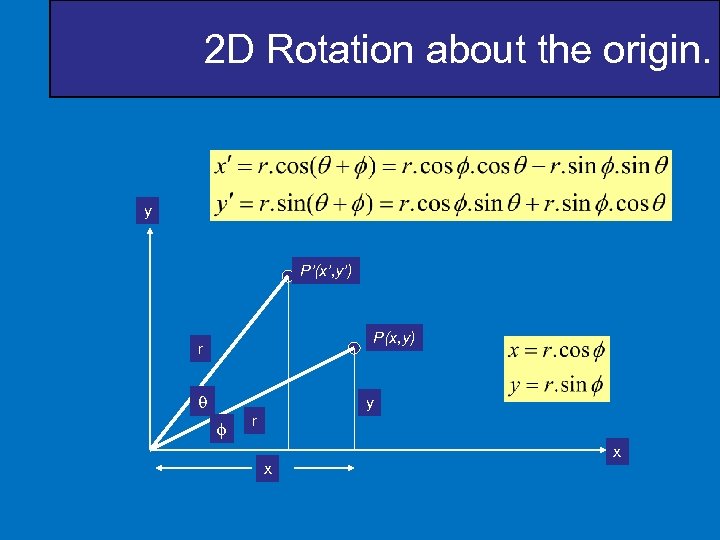2 D Rotation about the origin. Substituting for r : Gives us :

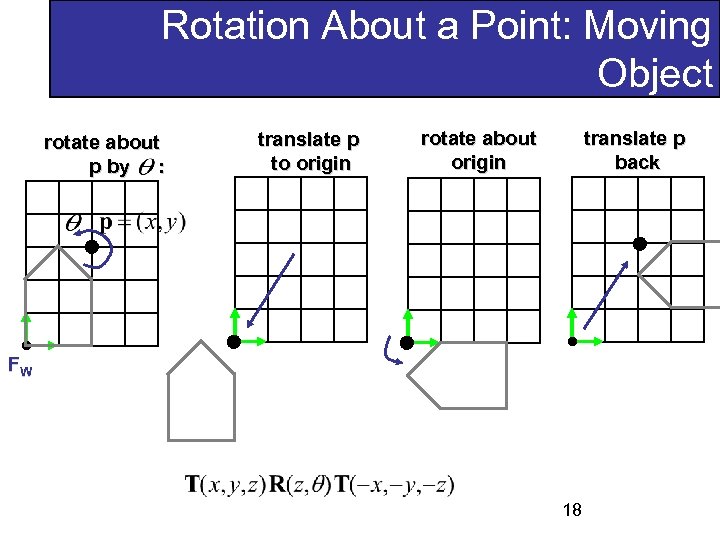Rotation About a Point: Moving Object rotate about p by : translate p to origin rotate about origin translate p back FW 18

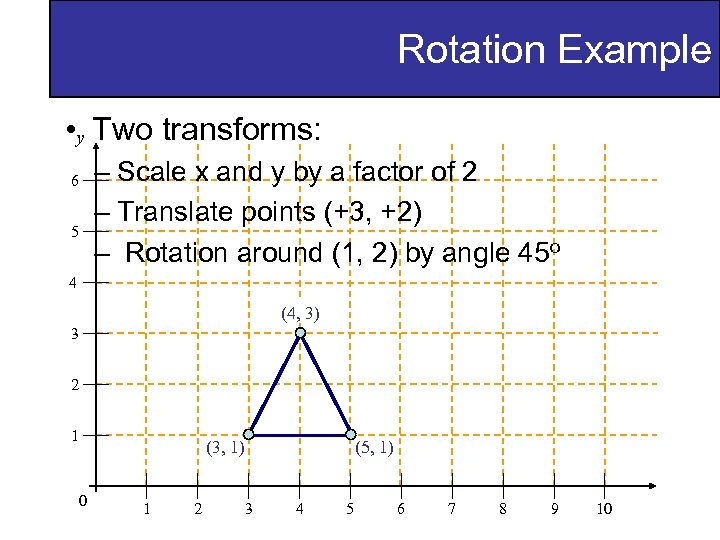Rotation Example • y Two transforms: – Scale x and y by a factor of 2 – Translate points (+3, +2) – Rotation around (1, 2) by angle 45 o 6 5 4 (4, 3) 3 2 1 (3, 1) 0 1 2 3 (5, 1) 4 5 6 7 8 9 10

Homogeneous Coordinates • Homogeneous representation of points: – Add an additional component w=1 to all points – All multiples of this vector are considered to represent the same 3 D point – why bother? need unified representation

21 of 25 Homogeneous Coordinates • Homogeneous coordinates – represent coordinates in 2 dimensions with a 3 -vector Homogeneous coordinates seem unintuitive, but they make graphics operations much easier

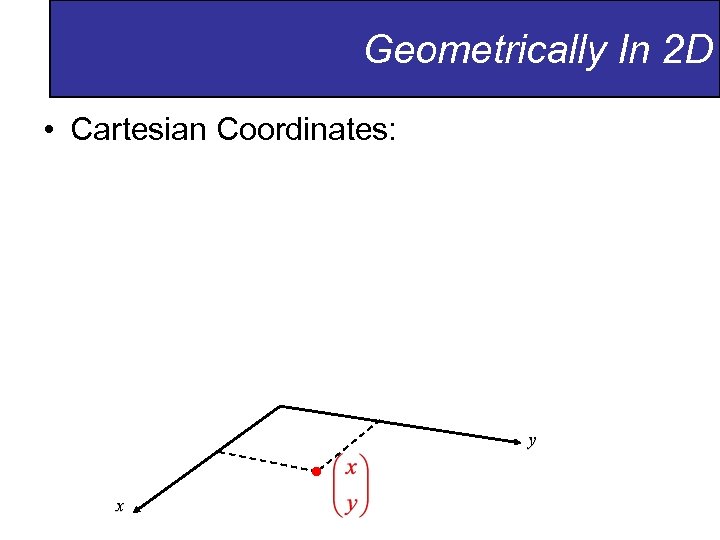Geometrically In 2 D • Cartesian Coordinates: y x

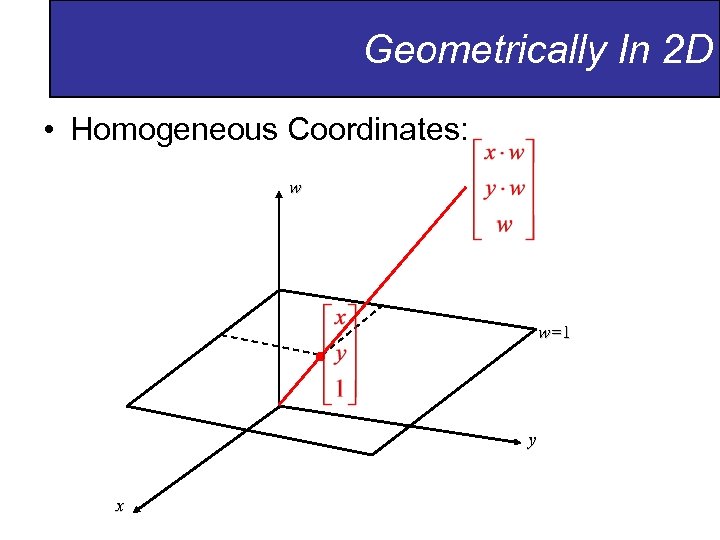Geometrically In 2 D • Homogeneous Coordinates: w w=1 y x

Homogeneous Coordinates A point (x, y) can be re-written in homogeneous coordinates as (xh, yh, h) The homogeneous parameter h is a nonzero value such that: We can then write any point (x, y) as (hx, hy, h) We can conveniently choose h = 1 so that (x, y) becomes (x, y, 1)

Why Homogeneous Coordinates? Mathematicians commonly use homogeneous coordinates as they allow scaling factors to be removed from equations We will see in a moment that all of the transformations we discussed previously can be represented as 3*3 matrices Using homogeneous coordinates allows us use matrix multiplication to calculate transformations – extremely efficient!

Homogeneous Coordinates • Q: How can we represent translation as a 3 x 3 matrix? • A: Using the rightmost column:

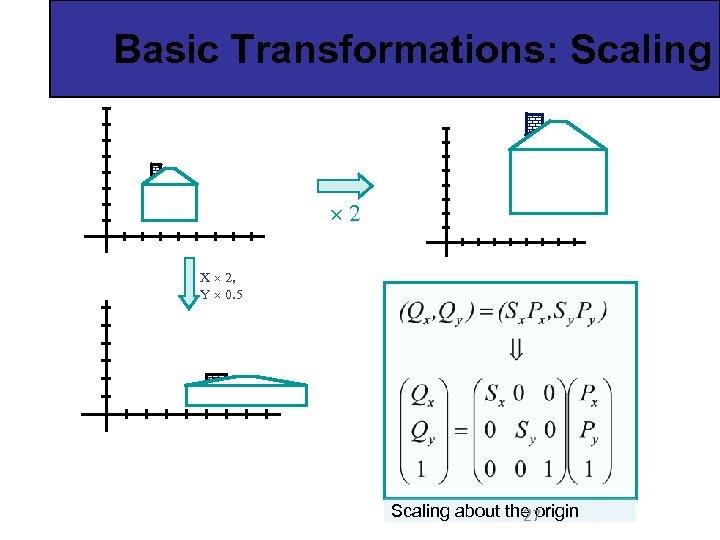Basic Transformations: Scaling 2 X 2, Y 0. 5 Scaling about the origin 27

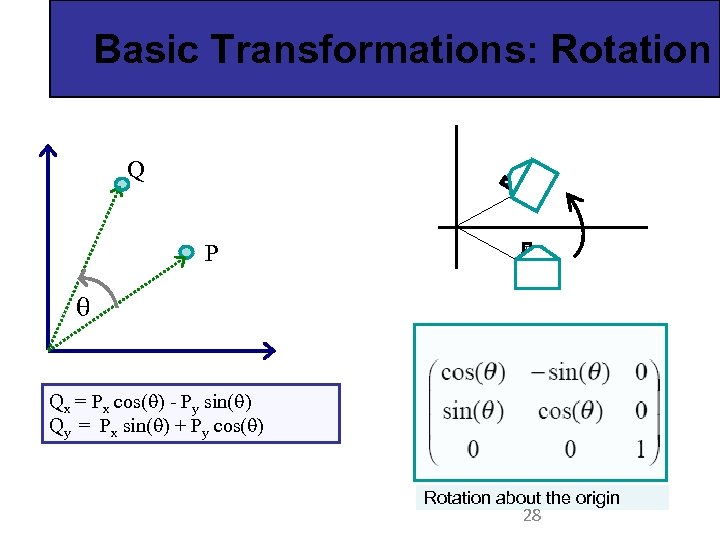Basic Transformations: Rotation Q P Qx = Px cos( ) - Py sin( ) Qy = Px sin( ) + Py cos( ) Rotation about the origin 28

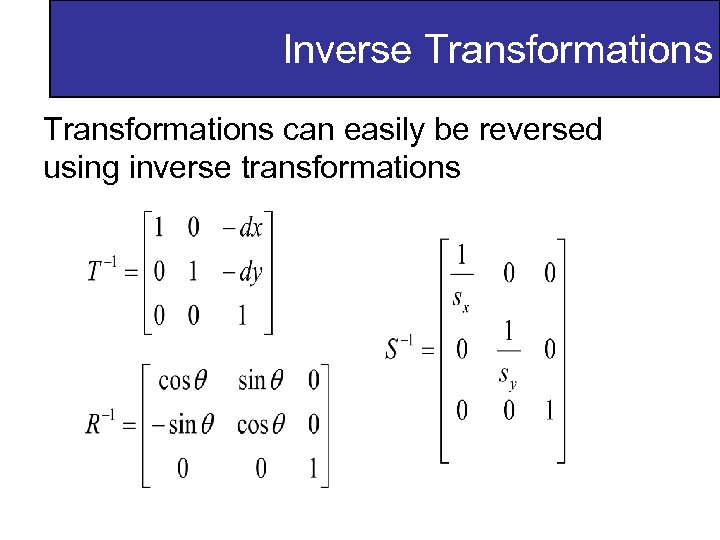Inverse Transformations can easily be reversed using inverse transformations

Combining Transformations A number of transformations can be combined into one matrix to make things easy – Allowed by the fact that we use homogenous coordinates Imagine rotating a polygon around a point other than the origin – Transform to centre point to origin – Rotate around origin – Transform back to centre point

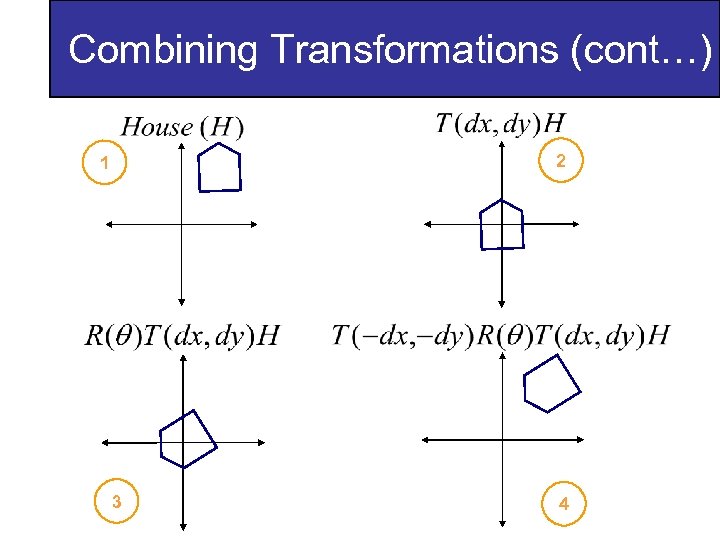Combining Transformations (cont…) 2 1 3 4

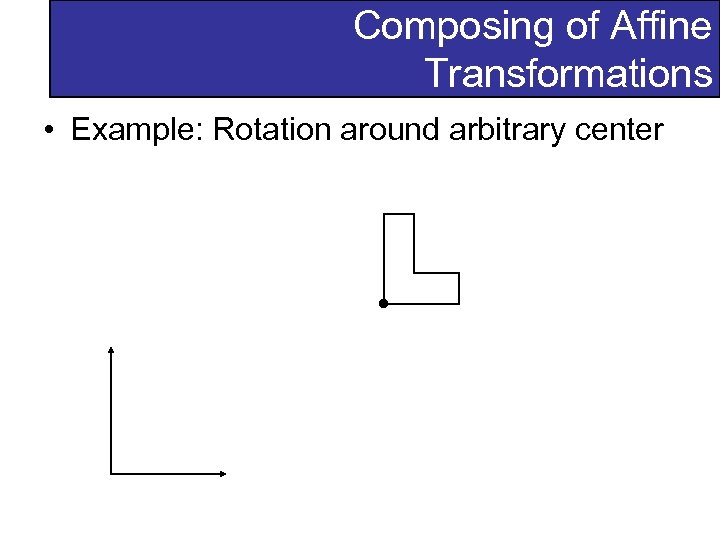Composing of Affine Transformations • Example: Rotation around arbitrary center

Composing of Affine Transformations • Example: Rotation around arbitrary center – Step 1: translate coordinate system to rotation center

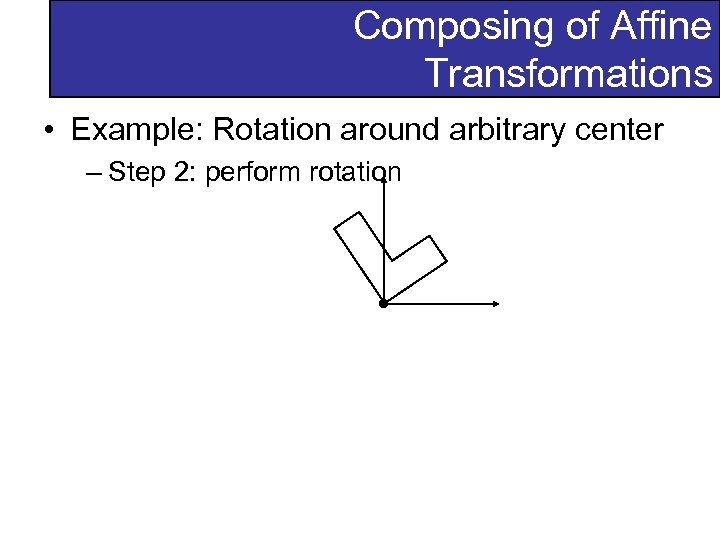Composing of Affine Transformations • Example: Rotation around arbitrary center – Step 2: perform rotation

Composing of Affine Transformations • Example: Rotation around arbitrary center – Step 3: back to original coordinate system

Combining Transformations (cont…) The three transformation matrices are combined as follows REMEMBER: Matrix multiplication is not commutative so order matters

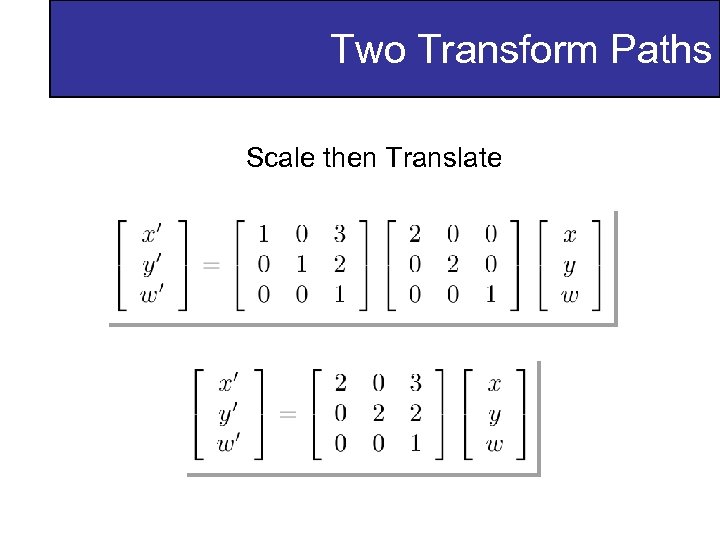Two Transform Paths Scale then Translate

38 of 25 Concatenation of scales.

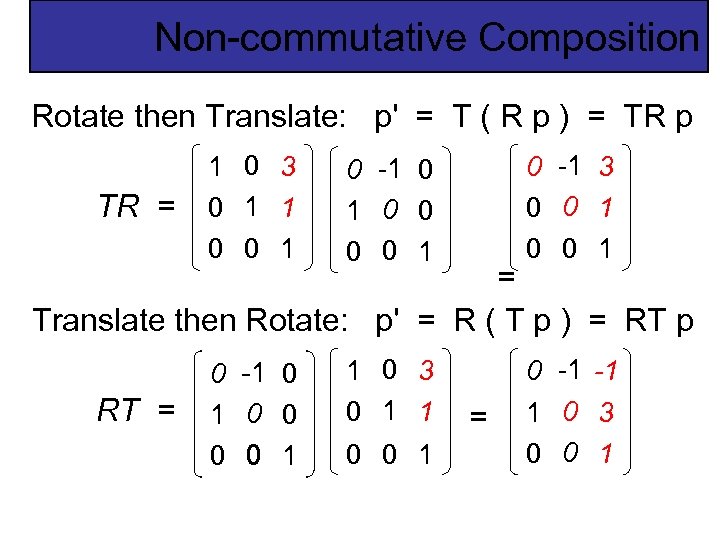Non-commutative Composition 39 of 25 Rotate then Translate: p' = T ( R p ) = TR p TR = 1 0 3 0 1 1 0 0 1 0 -1 0 0 0 0 1 0 -1 3 0 0 1 0 -1 0 0 0 0 1 1 0 3 0 1 1 0 -1 -1 1 0 3 0 0 1 = Translate then Rotate: p' = R ( T p ) = RT p RT = 02/10/09 Lecture 4 0 0 1 = 39

Exercises 1 Translate the shape below by (7, 2) y 6 5 4 (2, 3) 3 (1, 2) 2 (3, 2) 1 (2, 1) 0 1 2 3 4 5 6 7 8 9 10 x

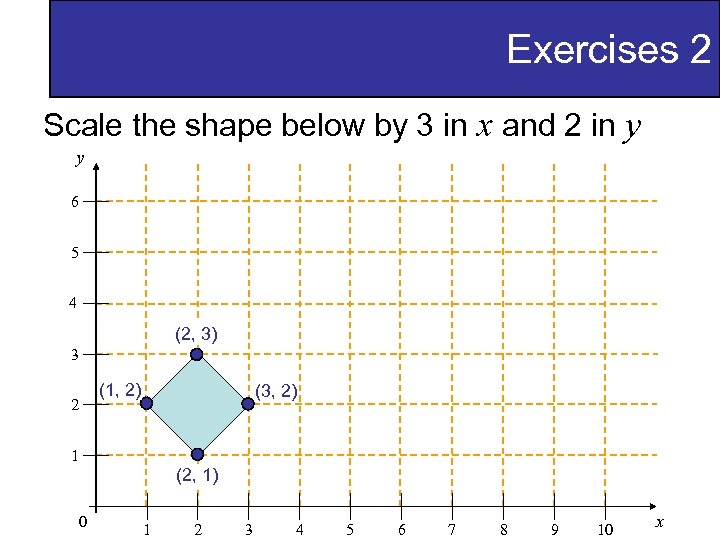Exercises 2 Scale the shape below by 3 in x and 2 in y y 6 5 4 (2, 3) 3 (1, 2) 2 (3, 2) 1 (2, 1) 0 1 2 3 4 5 6 7 8 9 10 x

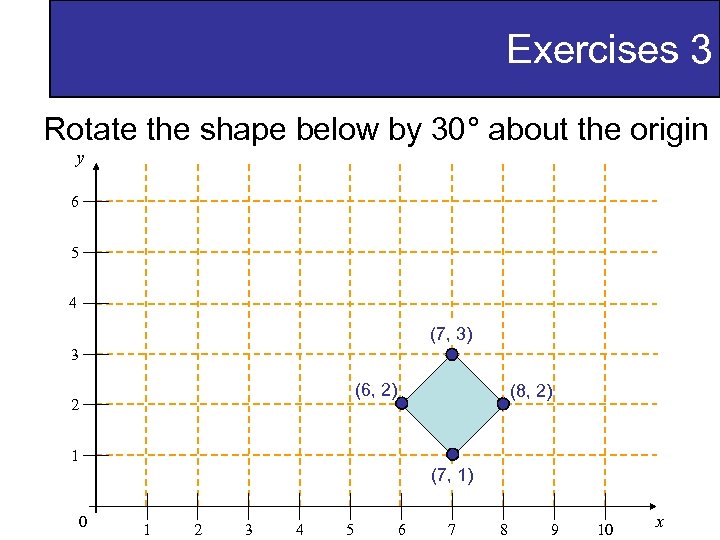Exercises 3 Rotate the shape below by 30° about the origin y 6 5 4 (7, 3) 3 (6, 2) 2 (8, 2) 1 (7, 1) 0 1 2 3 4 5 6 7 8 9 10 x

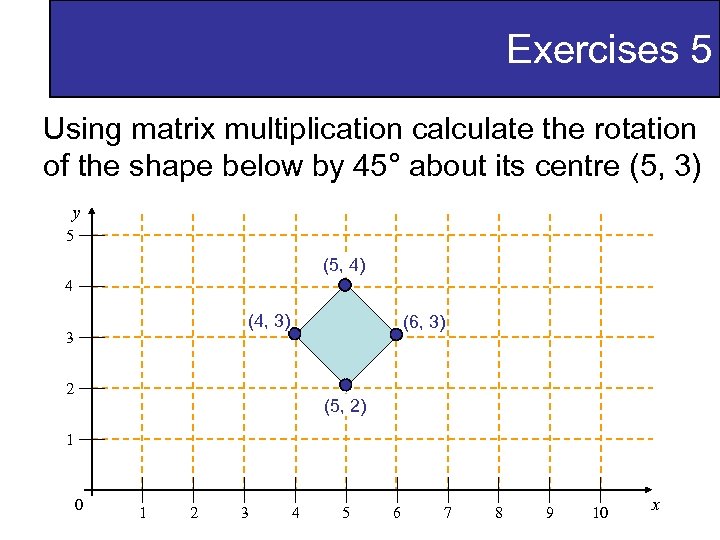Exercises 5 Using matrix multiplication calculate the rotation of the shape below by 45° about its centre (5, 3) y 5 (5, 4) 4 (4, 3) 3 (6, 3) 2 (5, 2) 1 0 1 2 3 4 5 6 7 8 9 10 x

44 of 25 This is convenient for character animation / robotics • In robotics / animation, we often want to know what is the current 3 D location of the end effectors (like the hand) • Can concatenate matrices from the origin of the body towards the end effecter 44

3 D Transformations. • Use homogeneous coordinates, just as in 2 D case. • Transformations are now 4 x 4 matrices. • We will use a right-handed (world) coordinate y system - ( z out of page ). x z (out of page)

46 of 25 Translation in 3 D. Simple extension to the 3 D case:

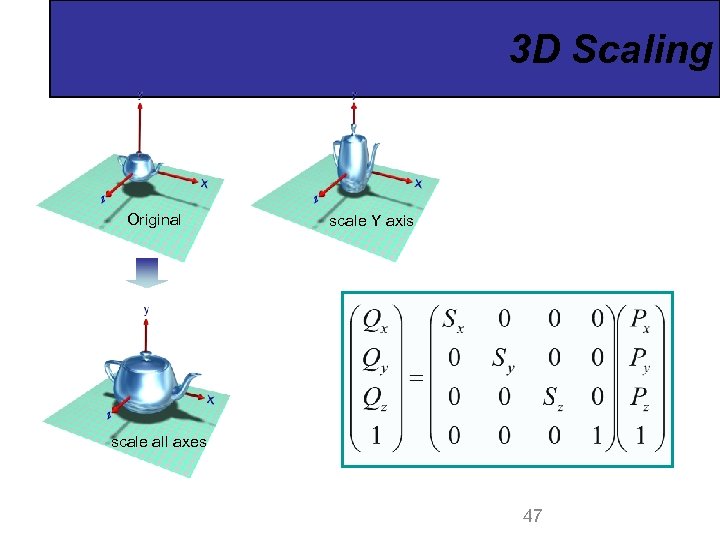3 D Scaling Original scale Y axis scale all axes 47

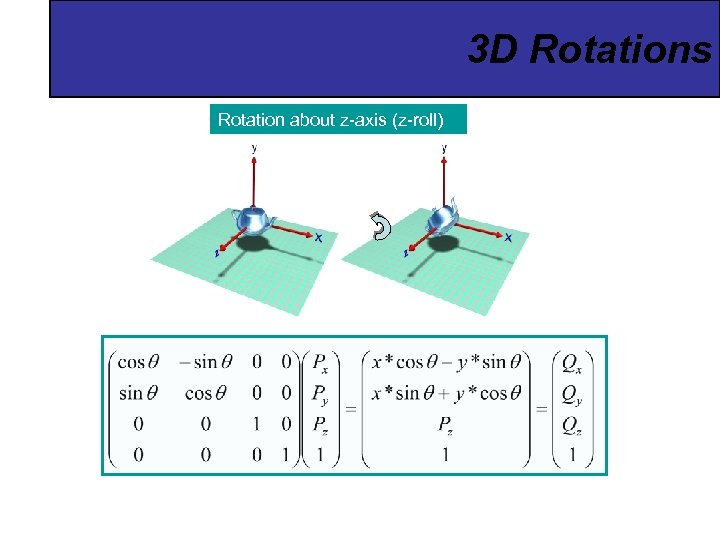3 D Rotations Rotation about z-axis (z-roll)

Rotating About the x-axis Rx( )

Rotating About the y-axis Ry( )

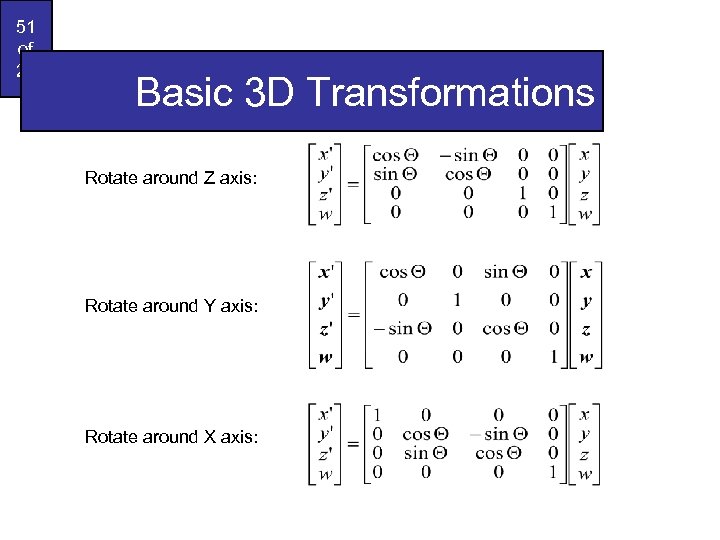51 of 25 Basic 3 D Transformations Rotate around Z axis: Rotate around Y axis: Rotate around X axis:

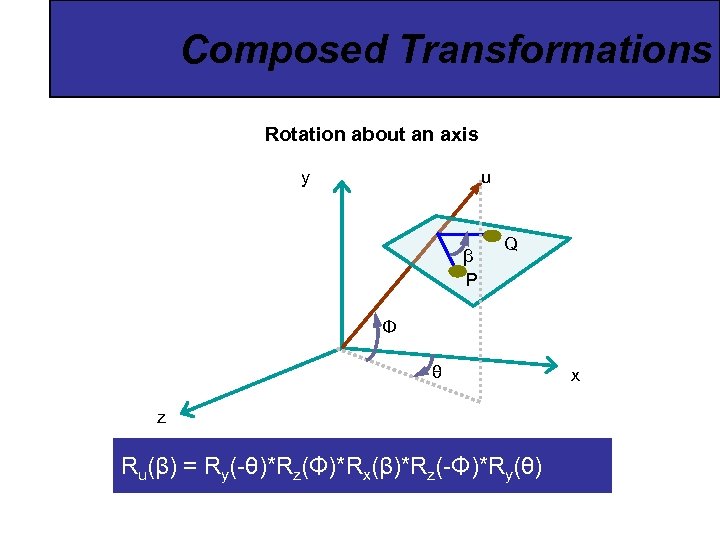Composed Transformations Rotation about an axis y u β P Q Φ θ z Ru(β) = Ry(-θ)*Rz(Φ)*Rx(β)*Rz(-Φ)*Ry(θ) x

53 of 25 Transform Left-Right, Right-Left Transforms between world coordinates and viewing coordinates. That is: between a right-handed set and a left-handed set.

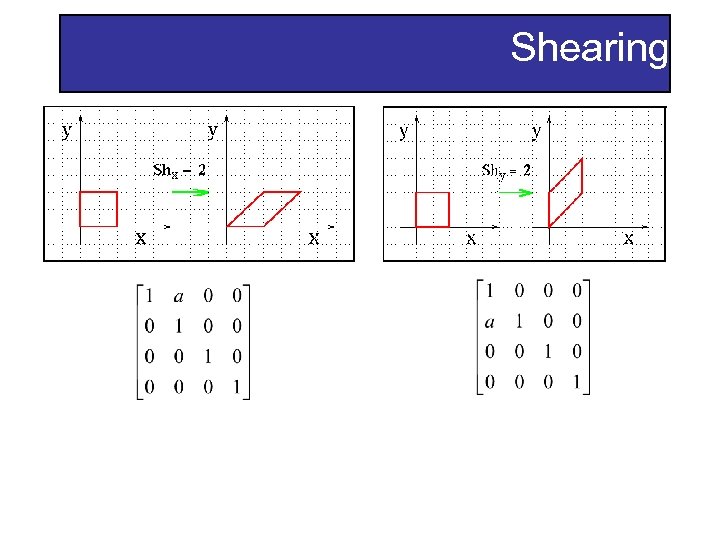Shearing

Shearing Horizontal Shear Vertical Shear y x s=0, No Shear s=1, 45 Degree She y x s is -tan(θ), where θ is the desired shear angle

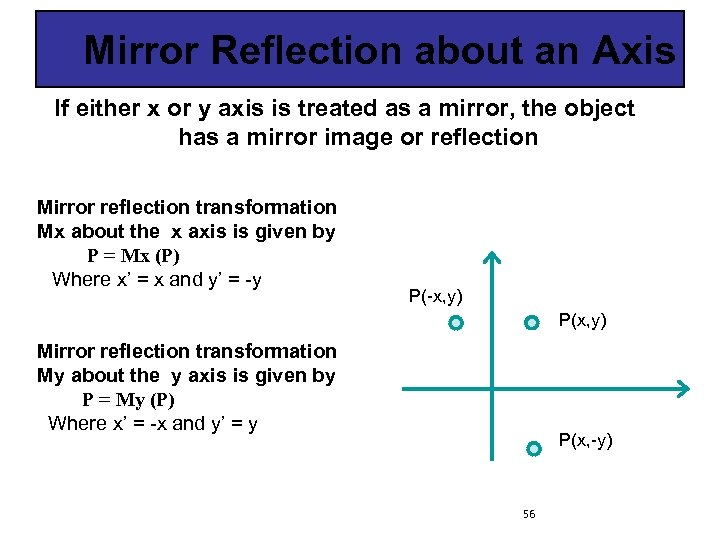Mirror Reflection about an Axis If either x or y axis is treated as a mirror, the object has a mirror image or reflection Mirror reflection transformation Mx about the x axis is given by P = Mx (P) Where x’ = x and y’ = -y P(-x, y) P(x, y) Mirror reflection transformation My about the y axis is given by P = My (P) Where x’ = -x and y’ = y P(x, -y) 56

Calculating the world coordinates of all vertices • For each object, there is a local-to-global transformation matrix • So we apply the transformations to all the vertices of each object • We now know the world coordinates of all the points in the scene 57

Open. GL Transformations • gl. Translate{fd}(TYPE x, TYPE y, TYPE z) – Multiply the current matrix by the translation matrix • gl. Rotate{fd}(TYPE angle, TYPE x, TYPE y, TYPE z) – Multiply the current matrix by the rotation matrix that rotates an object about the axis from (0, 0, 0) to (x, y, z) • gl. Scale{fd}(TYPE x, TYPE y, TYPE z) – Multiply the current matrix by the scale matrix