Computer Graphics Recitation 7 Motivation Image

Computer Graphics Recitation 7

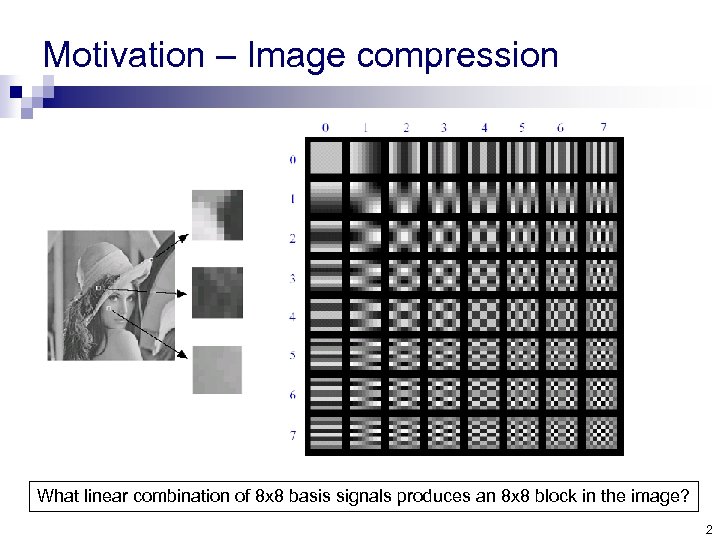Motivation – Image compression What linear combination of 8 x 8 basis signals produces an 8 x 8 block in the image? 2

The plan today n n Fourier Transform (FT). Discrete Cosine Transform (DCT). 3

What is a transformation? n n Function : rule that tells how to obtain result y given some input x Transformation : rule that tells how to obtain a function G(f) from another function g(t) 4

What do we need transformations for? n n n Mathematical tool to solve problems Change a quantity to another form that might exhibit useful features Example: XCVI x XII 96 x 12 = 1152 MCLII 5

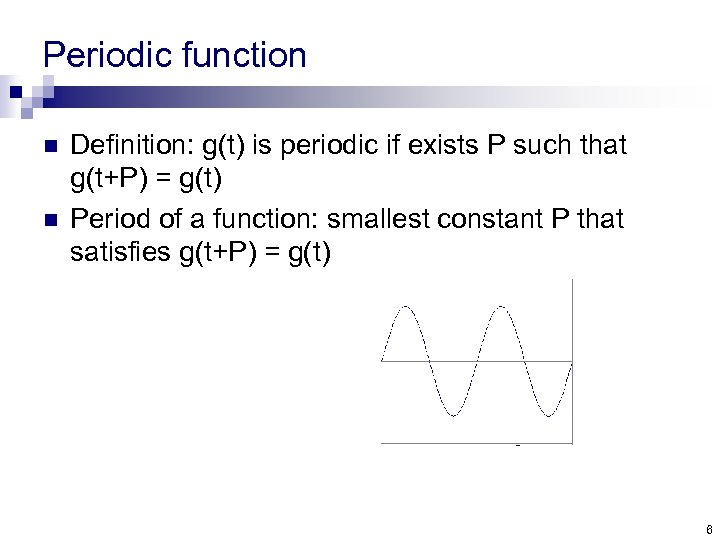Periodic function n n Definition: g(t) is periodic if exists P such that g(t+P) = g(t) Period of a function: smallest constant P that satisfies g(t+P) = g(t) 6

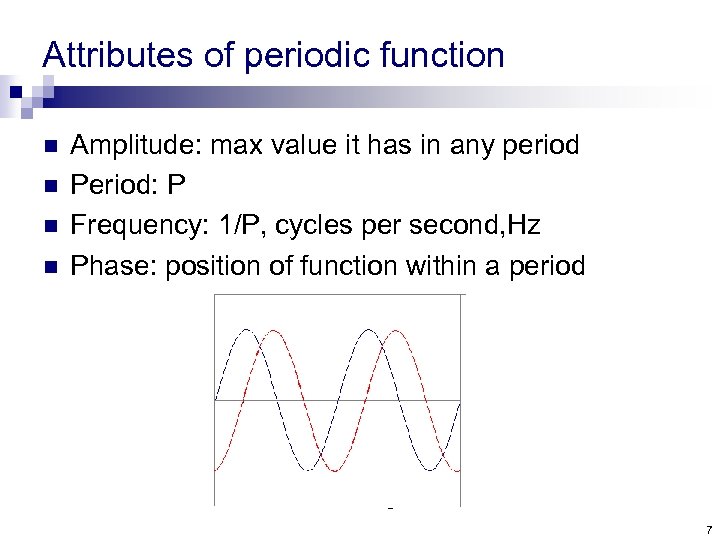Attributes of periodic function n n Amplitude: max value it has in any period Period: P Frequency: 1/P, cycles per second, Hz Phase: position of function within a period 7

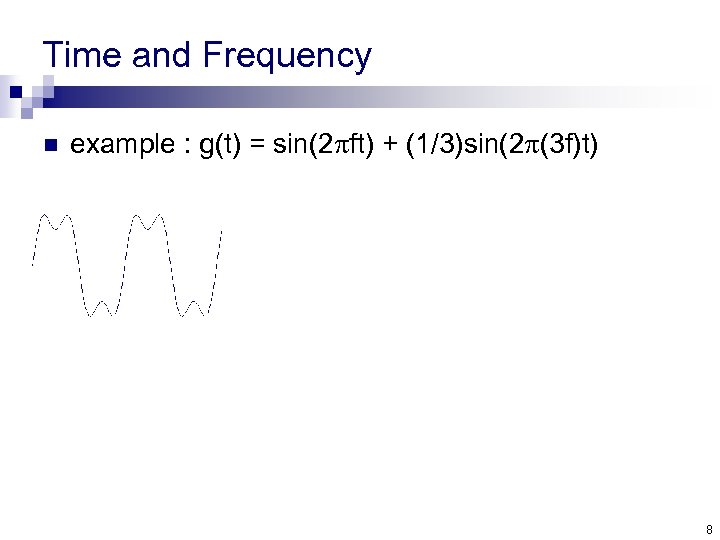Time and Frequency n example : g(t) = sin(2 pft) + (1/3)sin(2 p(3 f)t) 8

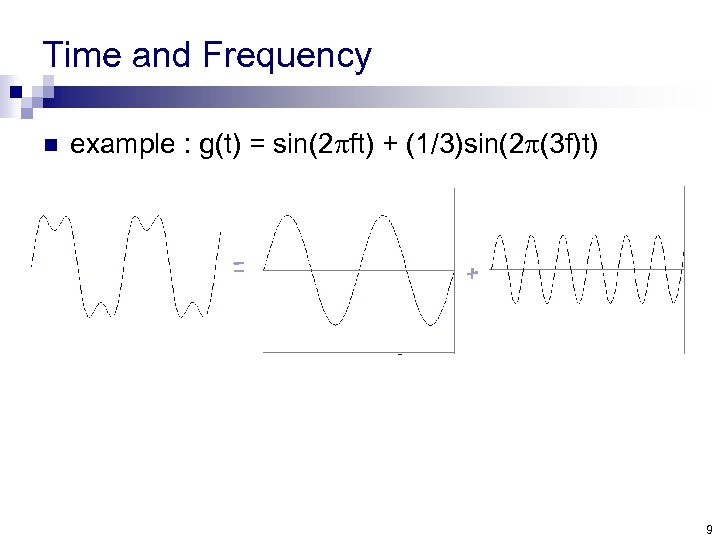Time and Frequency n example : g(t) = sin(2 pft) + (1/3)sin(2 p(3 f)t) = + 9

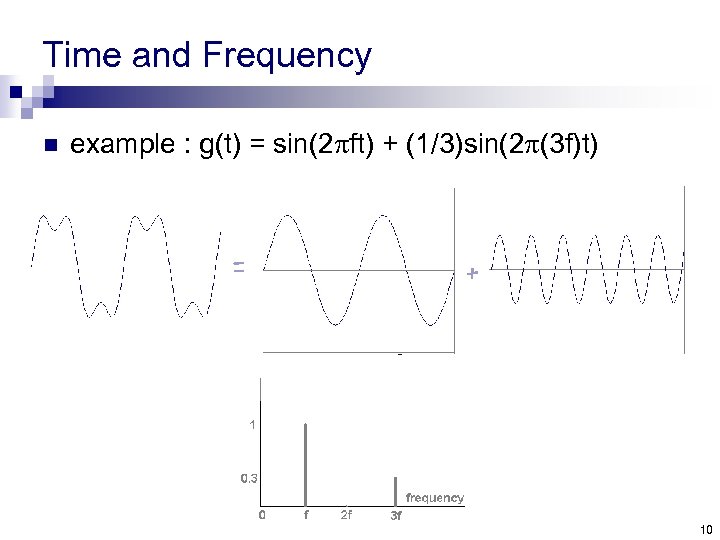Time and Frequency n example : g(t) = sin(2 pft) + (1/3)sin(2 p(3 f)t) = + 10

Time and Frequency n example : g(t) = { 1, -a/2 < t < a/2 0, elsewhere 11

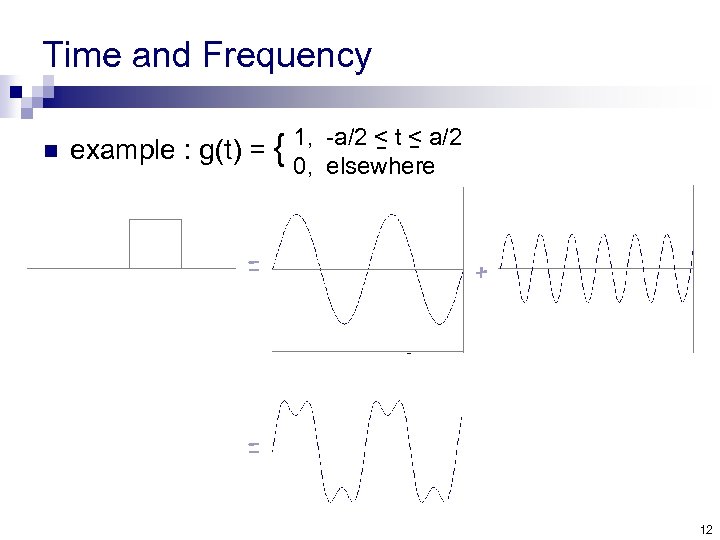Time and Frequency n example : g(t) = { = 1, -a/2 < t < a/2 0, elsewhere + = 12

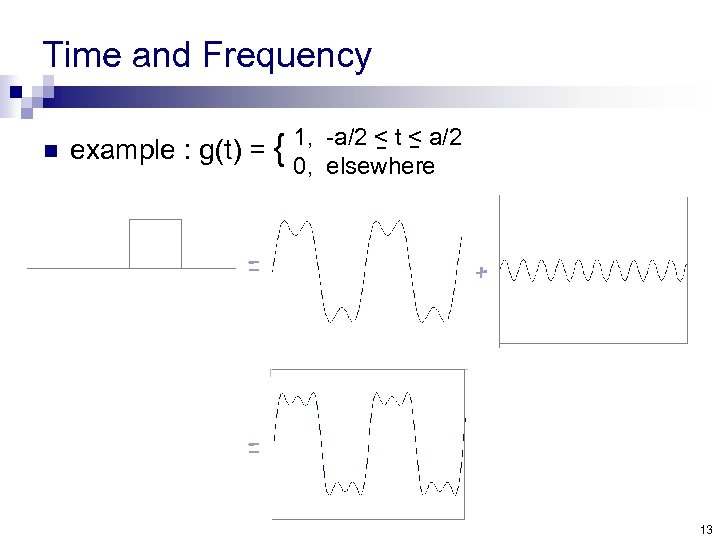Time and Frequency n example : g(t) = { = 1, -a/2 < t < a/2 0, elsewhere + = 13

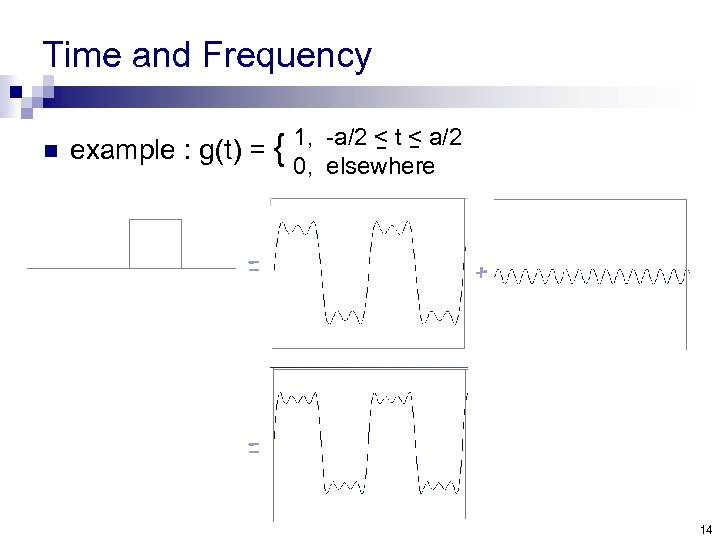Time and Frequency n example : g(t) = { = 1, -a/2 < t < a/2 0, elsewhere + = 14

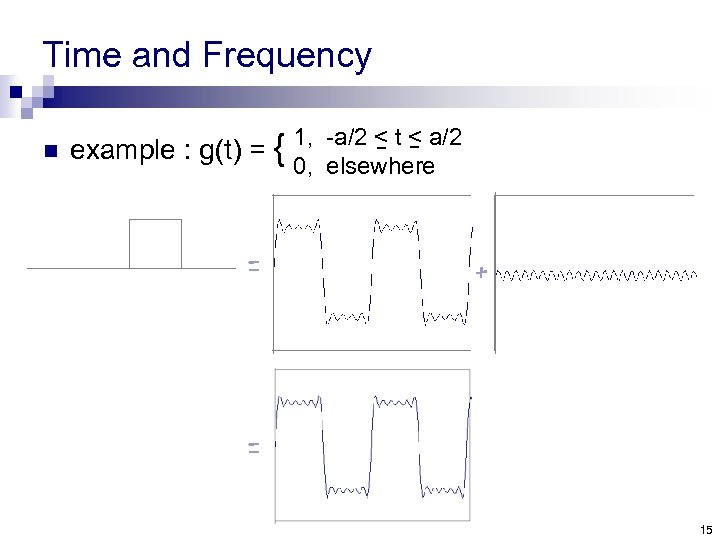Time and Frequency n example : g(t) = { = 1, -a/2 < t < a/2 0, elsewhere + = 15

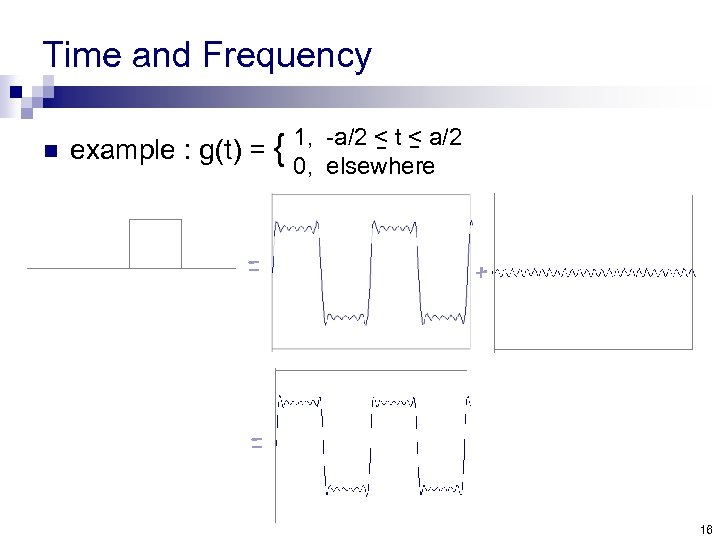Time and Frequency n example : g(t) = { = 1, -a/2 < t < a/2 0, elsewhere + = 16

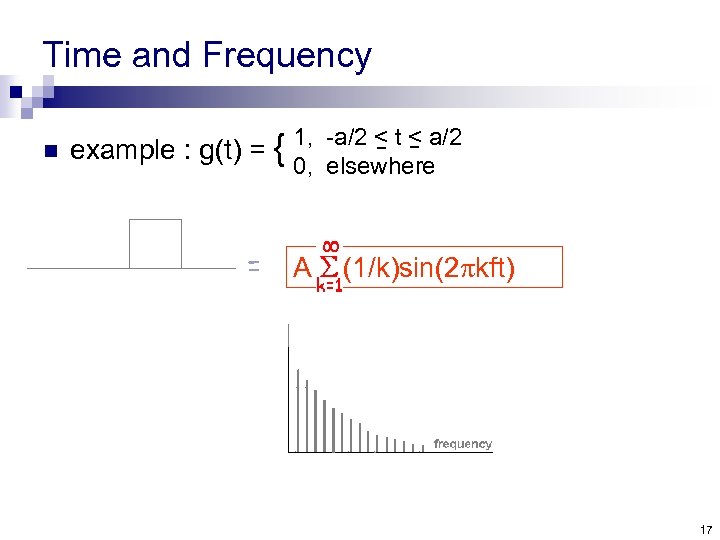Time and Frequency n example : g(t) = { = 1, -a/2 < t < a/2 0, elsewhere A (1/k)sin(2 pkft) 17

Time and Frequency § If the shape of the function is far from regular wave its Fourier expansion will include infinite num of freq. = A (1/k)sin(2 pkft) 18

Frequency domain § Spectrum of freq. domain : range of freq. § Bandwidth of freq. domain : width of the spectrum § DC component (direct current): component of zero freq. § AC – all others 19

Fourier transform § Every periodic function can be represented as the sum of sine and cosine functions § Transform a function between a time and freq. domain G(f) = g(t)[cos(2 pft) - i sin(2 pft)]dt g(t) = G(f)[cos(2 pft) + i sin(2 pft)]df 20

Fourier transform § Discrete G(f) = (1/n) g(t)[cos(2 pft/n) - i sin(2 pft/n)] , 0

FT for digitized image § Each pixel Pxy = point in 3 D (z coordinate is value of color/gray level § Each coefficient describes the 2 D sinusoidal function needed to reconstruct the surface § In typical image neighboring pixels have “close” values surface almost flat most FT coefficients small 22

Sampling theory § Image = continuous signal of intensity function i(t) § Sampling: store a finite sequence in memory i(1)…i(n) § The bigger the sample, the better the quality? – not necessarily 23

Sampling theory § We can sample an image and reconstruct it without loss of quality if we can : - Transform i(t) function from time to freq. Domain - Find the max freq. fm - Sample i(t) at rate > 2 fm - Store the sampled values in a bitmap 24

Sampling theory § Some loss of image quality because: - fm can be infinite: choose a value s. t freq. > fm do not contribute much (low amplitudes) - Bitmap may be too small § 2 fm is Nyquist rate 25

Fourier Transform § Periodic function can be represented as sum of sine waves that are integer multiple of fundamental (basis) frequencies § Freq. domain can be applied to a non periodic function if it is nonzero over a finite range 26

Discrete Cosine Transform § A variant of discrete Fourier transform - Real numbers - Fast implementation -Separable (row/column) 27

Discrete Cosine Transform § Example: DCT on 8 points G = (½) Cf f Pt cos((2 t+1)fp/16) , C f = { 1 f=0 f=1… 7 § Fourier transform on 8 points Gf = Pt cos(2 pft/8) – i Pt sin(2 pft/8) , f=0, 1, …, 7 28

Discrete Cosine Transform § Example 8 points: Same meaning: the 8 numbers Gf tell what sinusoidal func. should be combined to approximate the function described by the 8 original numbers Pt 29

Discrete Cosine Transform § Example 8 points: G = (½) Cf f Pt cos((2 t+1)fp/16) , C f = { 1 f=0 f=1… 7 § G 3 = contribution of sinusoidal with freq. 3 tp/16 to the 8 numbers Pt § G 7 = contribution of sinusoidal with freq. 7 tp/16 to the 8 numbers Pt 30

Discrete Cosine Transform § Example 8 points: The inverse DCT Pt = (½) C j G j cos((2 t+1)jp/16) , t=0, 1, …, 7 31

Discrete Cosine Transform § 2 D DCT G ij = C i. C j Pxy cos((2 x+1)ip/2 n)cos((2 y+1)jp/2 n) § 2 D Inverse DCT (IDCT) Pxy =¼ C i. C j Gij cos((2 x+1)ip/16) cos((2 y+1)jp/16) C f={1 f=0 f=1… 7 32

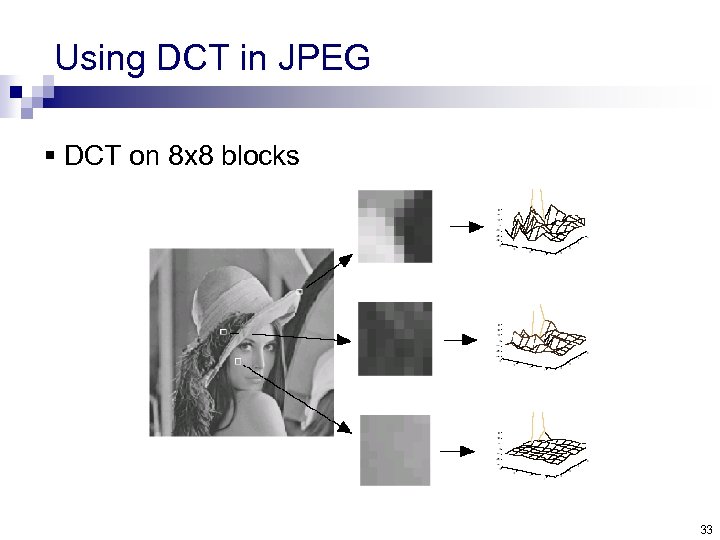Using DCT in JPEG § DCT on 8 x 8 blocks 33

Using DCT in JPEG § Block size : small block - faster - correlation exists between neighboring pixels large block - better compression in “flat” regions § Power of 2 – for fast implementation 34

Using DCT in JPEG § DCT – basis 35

Using DCT in JPEG § For almost flat surface most Gij=0 § For surface that oscillates much many Gij non zero § G 00 = DC coefficient § Numbers at top left of Gij contribution of low freq. sinusoidal to the surface, bottom right – high freq. 36

Using DCT in JPEG §Numbers at top left of Gij contribution of low freq. sinusoidal to the surface, bottom right – high freq. § Scan each block in zig-zag order 37

Image compression using DCT • DCT enables image compression by concentrating most image information in the low frequencies • Loose unimportant image info buy cut Gij at right bottom • Decoder computes the inverse IDCT 38

See you next time