Computer Graphic 2 D Transformation Outline 1

Computer Graphic 2 D Transformation

Outline 1. Why transformations ? 2. Basic 2 D Transformations ØTranslation Ø Scaling ØRotation 3. Homogeneous Coordinate system 4. Composite Transformations 5. Reflection and Shearing

Why transformations ? n In graphics, once we have an object described, transformations are used to move that object, scale it and rotate it

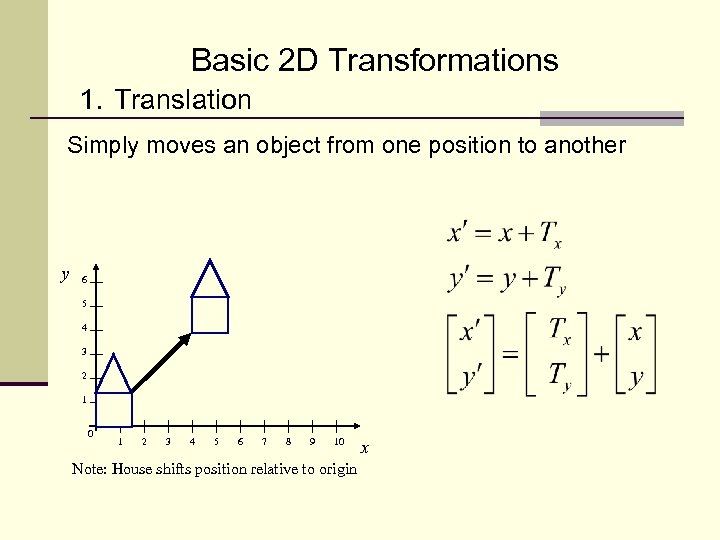Basic 2 D Transformations 1. Translation Simply moves an object from one position to another y 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 10 Note: House shifts position relative to origin x

2 D Translation w Moving a polygon from position (a) to position (b) with the translation vector (-5, 10), i. e. y y 20 20 15 15 p 3(15, 10) 10 5 P 1(10, 5) 5 10 P 2(20, 5) 10 15 (a) 20 x 5 5 10 15 (b) 20 x

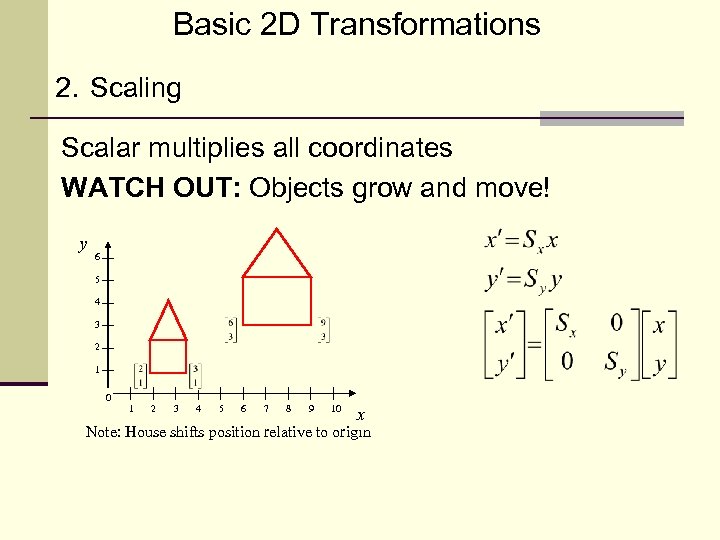Basic 2 D Transformations 2. Scaling Scalar multiplies all coordinates WATCH OUT: Objects grow and move! y 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 10 x Note: House shifts position relative to origin

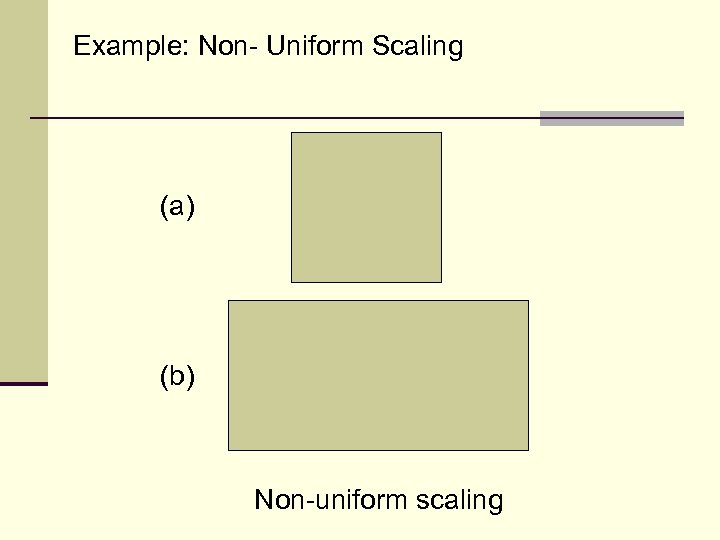Example: Non- Uniform Scaling (a) (b) Non-uniform scaling

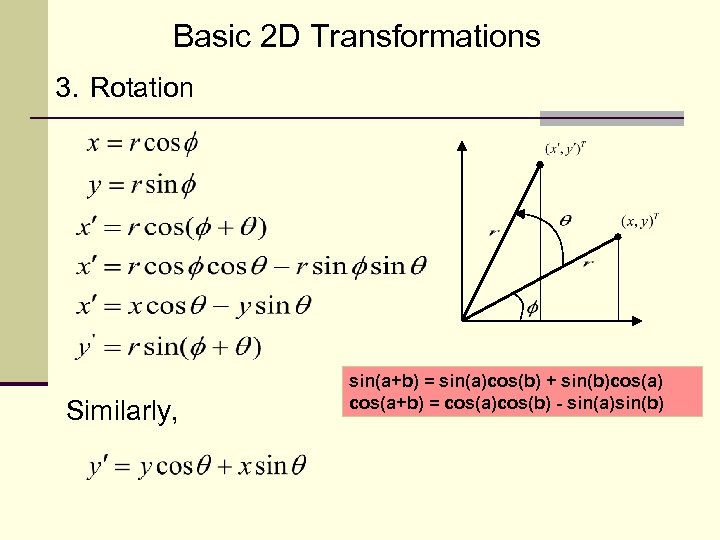Basic 2 D Transformations 3. Rotation Similarly, sin(a+b) = sin(a)cos(b) + sin(b)cos(a) cos(a+b) = cos(a)cos(b) - sin(a)sin(b)

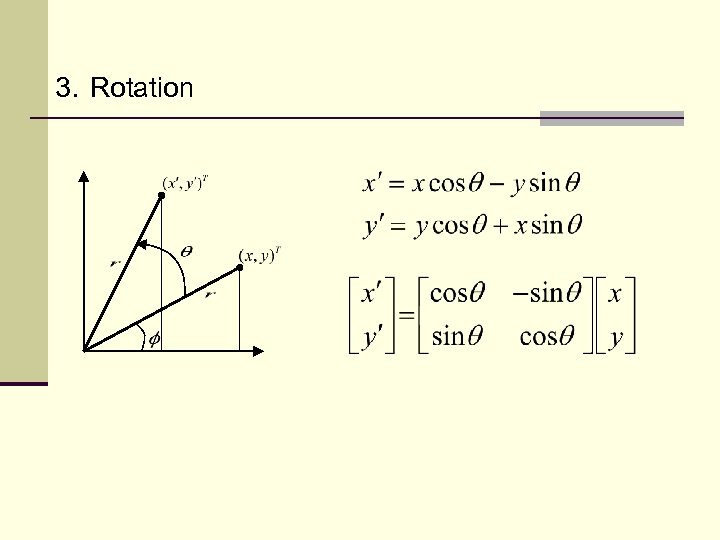3. Rotation

Homogenous Coordinates Ø A point (x, y) can be re-written in homogeneous coordinates as (xh, yh, h) Ø The homogeneous parameter h is a nonzero value such that: Ø We can then write any point (x, y) as (hx, hy, h) Ø We can conveniently choose h = 1 so that (x, y) becomes (x, y, 1)

Why Homogenous Coordinates? Ø Mathematicians commonly use homogeneous coordinates as they allow scaling factors to be removed from equations Ø We will see in a moment that all of the transformations we discussed previously can be represented as 3*3 matrices Ø Using homogeneous coordinates allows us use matrix multiplication to calculate transformations – extremely efficient!

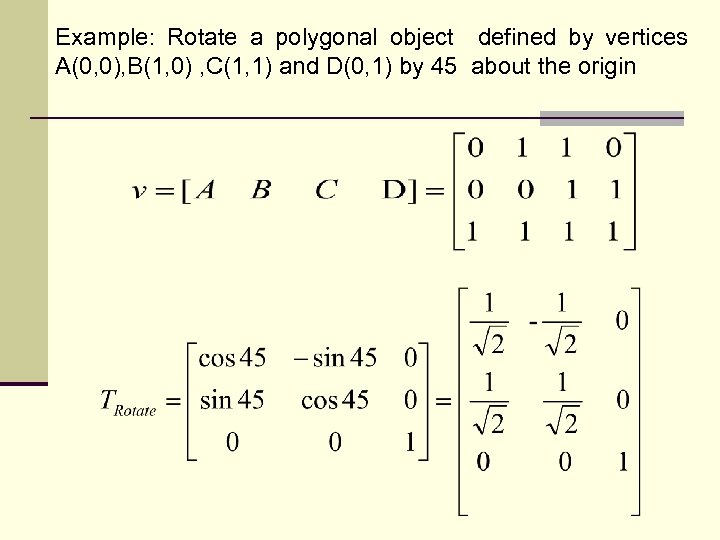Example: Rotate a polygonal object defined by vertices A(0, 0), B(1, 0) , C(1, 1) and D(0, 1) by 45 about the origin

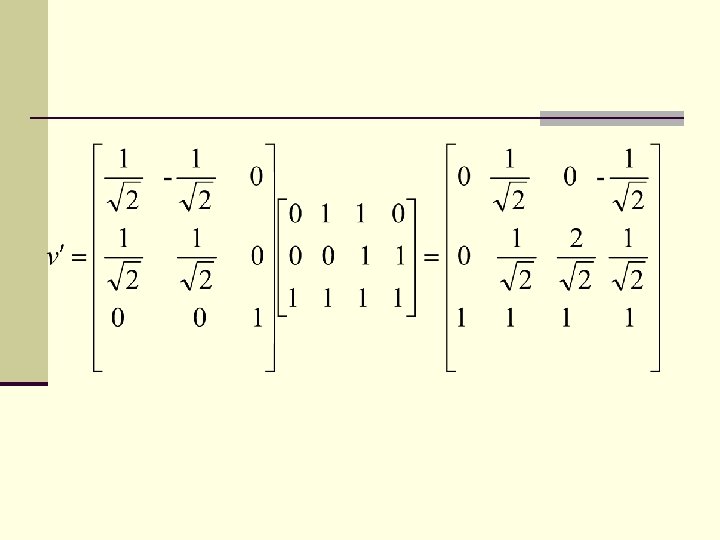
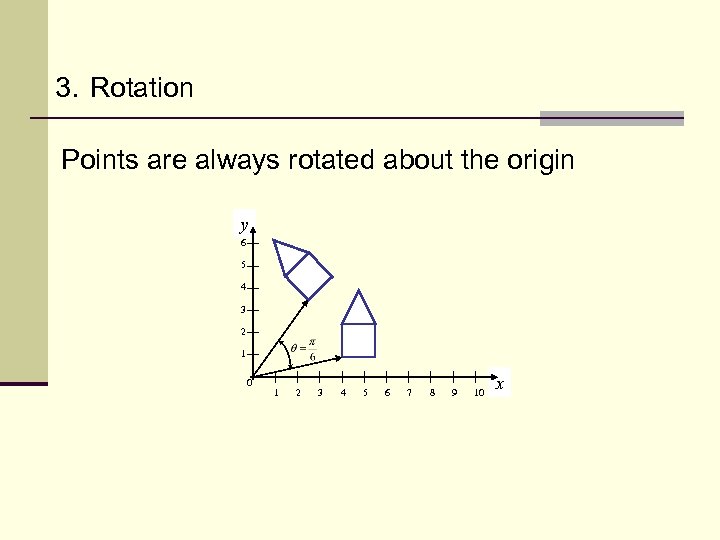3. Rotation Points are always rotated about the origin y 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 10 x

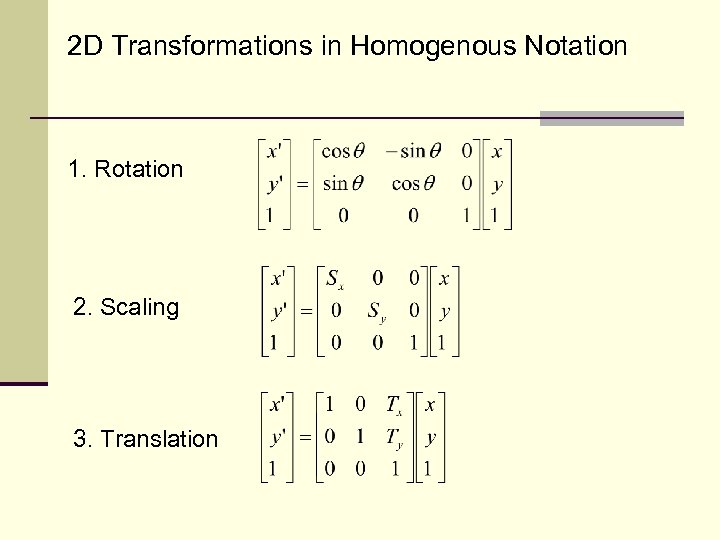2 D Transformations in Homogenous Notation 1. Rotation 2. Scaling 3. Translation

Inverse Transformations 1. Inverse of Rotation 2. Inverse of Scaling 3. Inverse of Translation

Example w Consider the line with endpoints (10, 10) and (30, 25). Translate it by tx = -20, ty = -10 and then rotate it by θ = 90º. y (30, 25) (10, 10) Right-to-left x

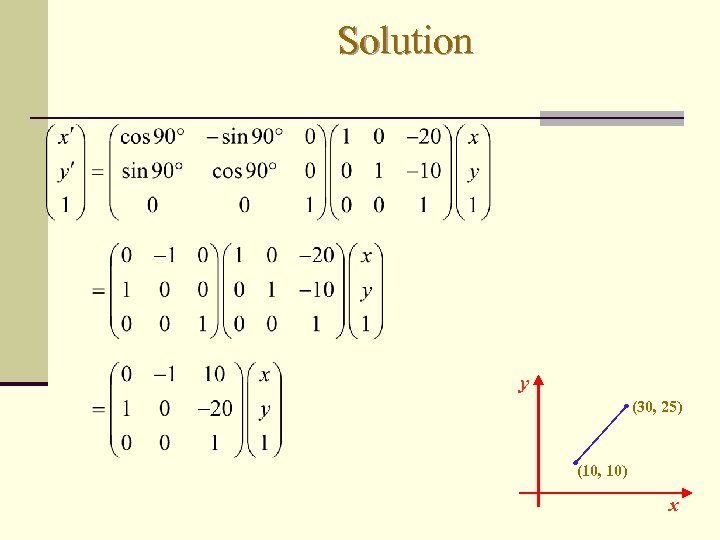Solution y (30, 25) (10, 10) x

Solution (continue) y (30, 25) (-15, 10) (10, 10) (0, -10) Point (10, 10) Point (30, 25) x

Exercises w Consider the following object: y 25 10 10 45 x 1. Apply a rotation by 145º then scale it by Sx=2 and Sy=1. 5 and then translate it by tx=20 and ty=-30. 2. Scale it by Sx=½ and Sy=2 and then rotate it by 30º. 3. Apply a rotation by 90º and then another rotation by 45º. 4. Apply a rotation by 135º.

Scaling about a Reference Point If the center of the object is not at the origin, in this case we should consider a scaling as a composite transformation which involves the following steps. 1. Translation of the reference (xc, yc) to the origin 2. Scale the object by scale factor by (Sx, Sy) 3. Translation of the reference point back to its original position

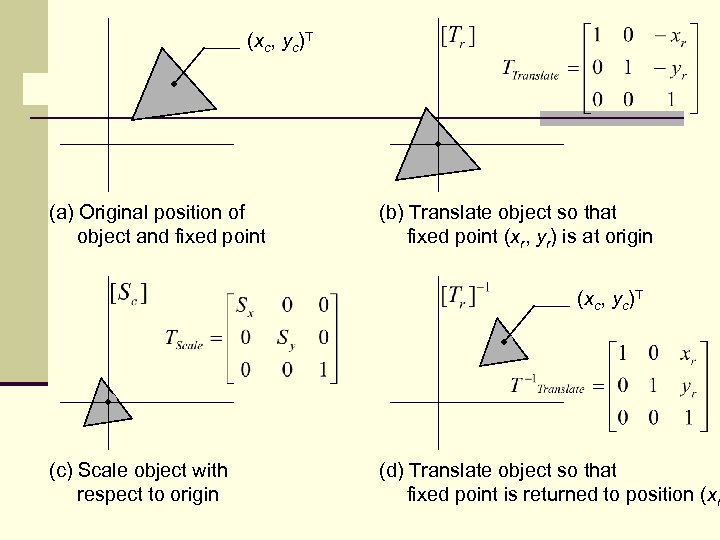(xc, yc)T (a) Original position of object and fixed point (b) Translate object so that fixed point (xr, yr) is at origin (xc, yc)T (c) Scale object with respect to origin (d) Translate object so that fixed point is returned to position (xr

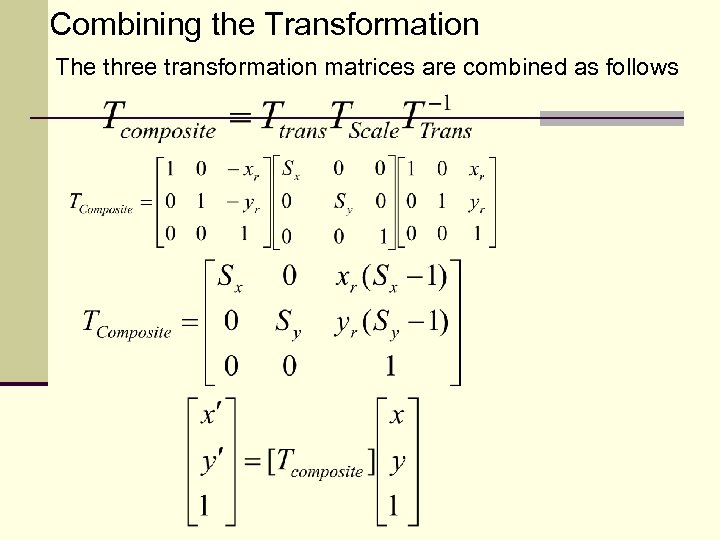Combining the Transformation The three transformation matrices are combined as follows

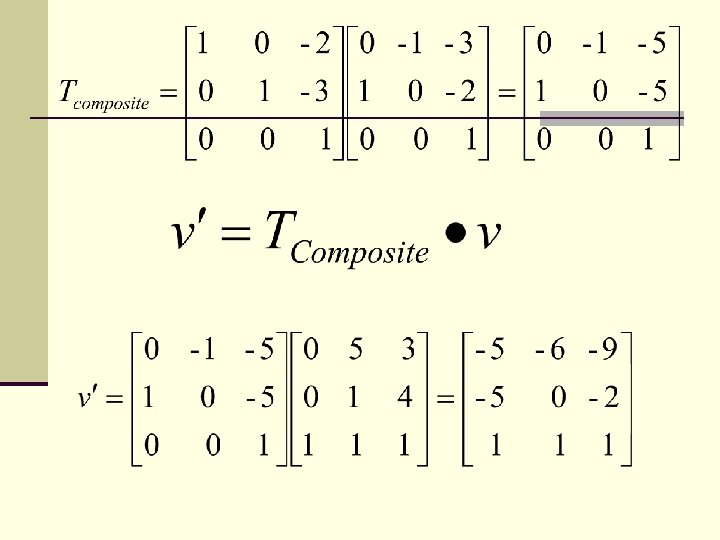
Example 1: Consider a triangle having a vertices at A(0, 0), B(5, 1), and C(3, 4) scale this triangle using scaling factors Sx=2 and Sy=1 about a) the origin b) about the reference point (2, 3) a) At origin ( xr=0, yr=0)

b) Scaling about the reference point (2, 3) : Here, the transformation matrix

Rotation about an Arbitrary Point Rotation about an arbitrary point is composite transformation. This operation involve s three basic transformations: 1. Translation of the object center (xc, yc) to the origin 2. Rotation of the object about the origin by angle θ in. say, the anticlockwise direction 3. Translation of the rotated object back to its original position

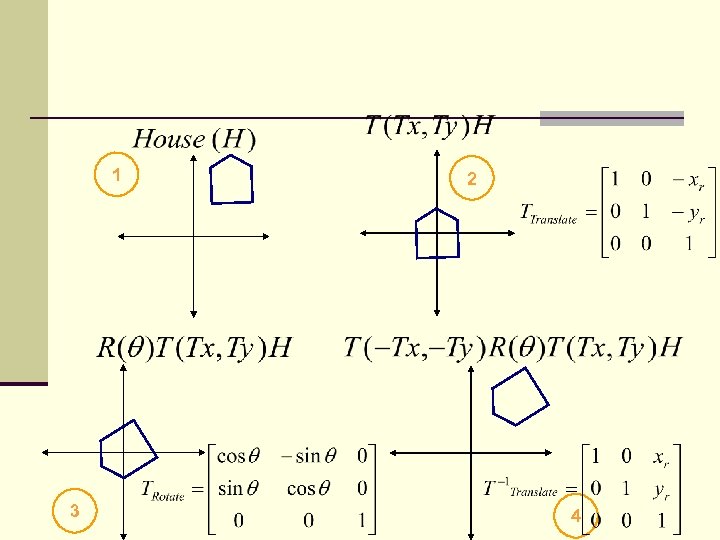1 3 2 4

Example: Consider a triangle having a vertices at A(0, 0), B(5, 1), and C(3, 4) scale this triangle. Rotate the triangle by 90 about a) the origin b) about the reference point (2, 3) Solution: a) about the origin The transformation matrix for rotation about the origin :

b) Rotation about point (2, 3 )

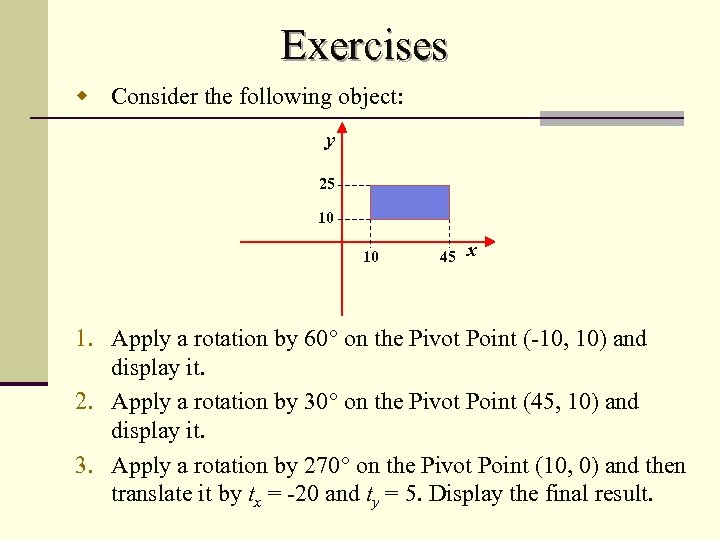Exercises w Consider the following object: y 25 10 10 45 x 1. Apply a rotation by 60° on the Pivot Point (-10, 10) and display it. 2. Apply a rotation by 30° on the Pivot Point (45, 10) and display it. 3. Apply a rotation by 270° on the Pivot Point (10, 0) and then translate it by tx = -20 and ty = 5. Display the final result.

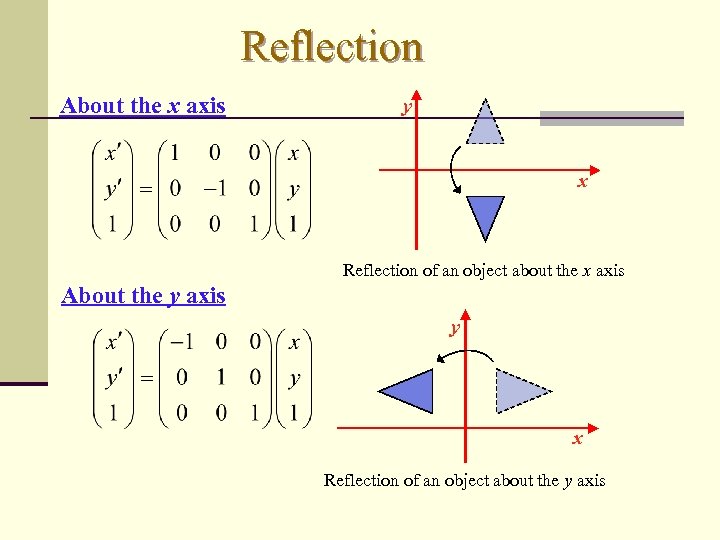Reflection About the x axis y x Reflection of an object about the x axis About the y axis y x Reflection of an object about the y axis

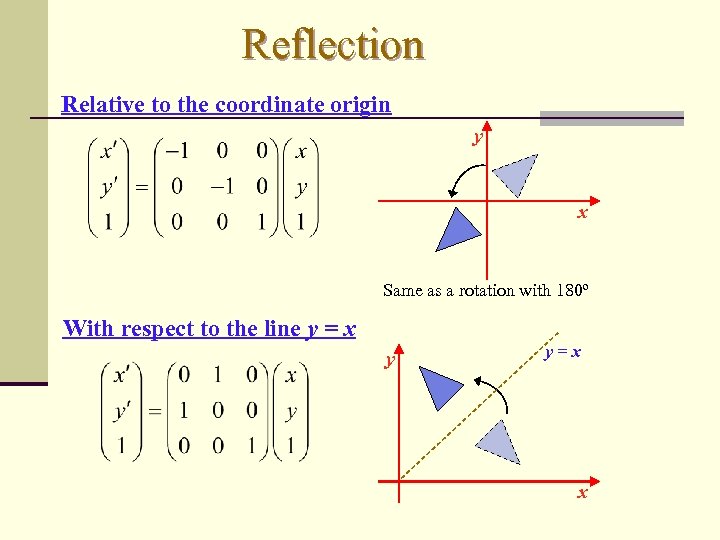Reflection Relative to the coordinate origin y x Same as a rotation with 180º With respect to the line y = x y y=x x

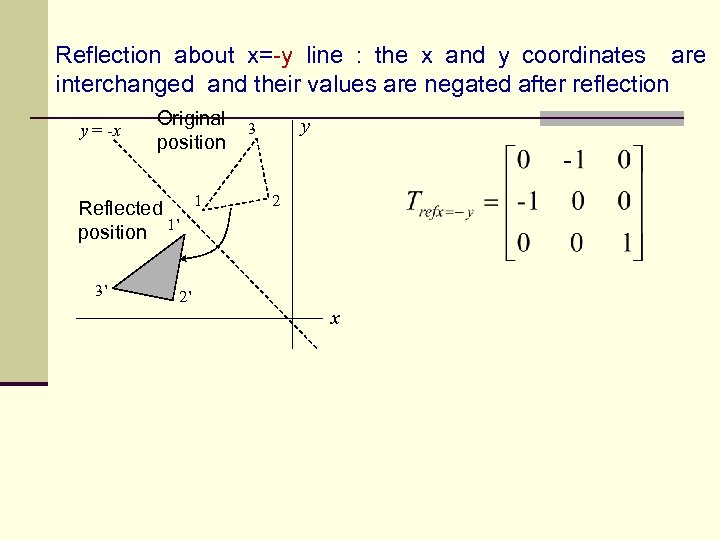Reflection about x=-y line : the x and y coordinates are interchanged and their values are negated after reflection y = -x Original position Reflected position 1’ 3’ 1 y 3 2 2’ x

Reflection about any arbitrary line: y=mx+b This kind of reflection can be implemented by a sequence of the following steps: I. Translate the line, along the y-axis so that it pass the origin II. Rotate through an angle θ =tan-1(m) in clockwise so that the line is aligned with x-axis III. Reflect the object about x-axis IV. Perform inverse Rotation and Translation

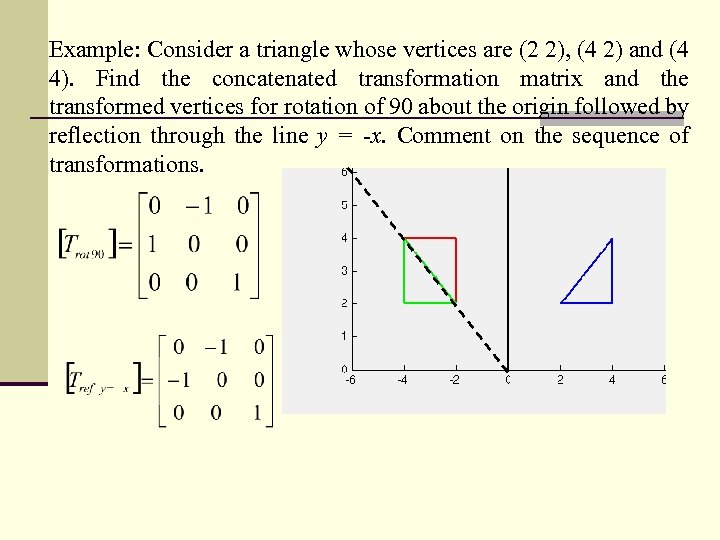Example: Consider a triangle whose vertices are (2 2), (4 2) and (4 4). Find the concatenated transformation matrix and the transformed vertices for rotation of 90 about the origin followed by reflection through the line y = -x. Comment on the sequence of transformations.

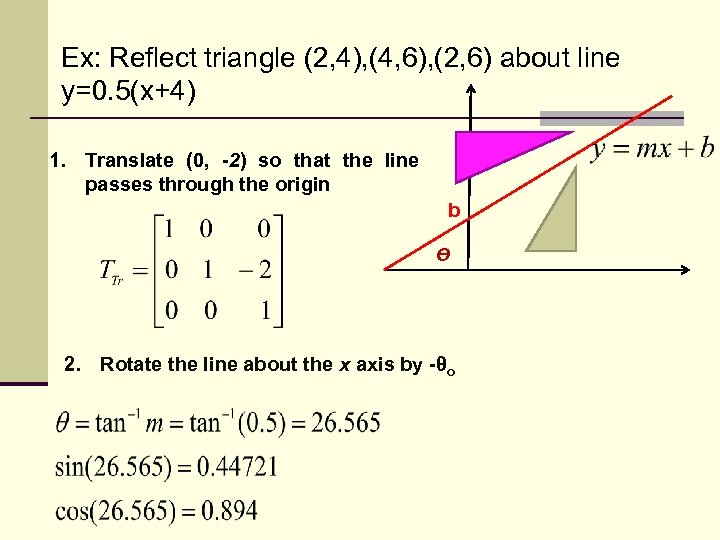Ex: Reflect triangle (2, 4), (4, 6), (2, 6) about line y=0. 5(x+4) 1. Translate (0, -2) so that the line passes through the origin b ϴ 2. Rotate the line about the x axis by -θo

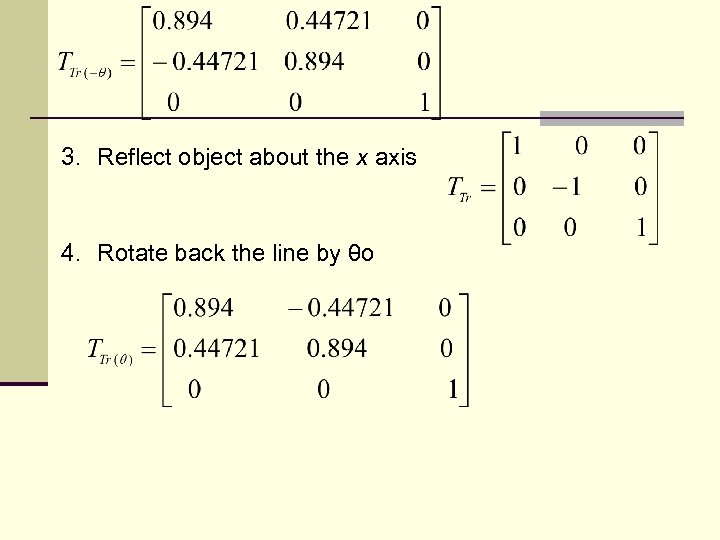3. Reflect object about the x axis 4. Rotate back the line by θo

5. Translate back (0, 2)

The final position of line after reflection about the line is

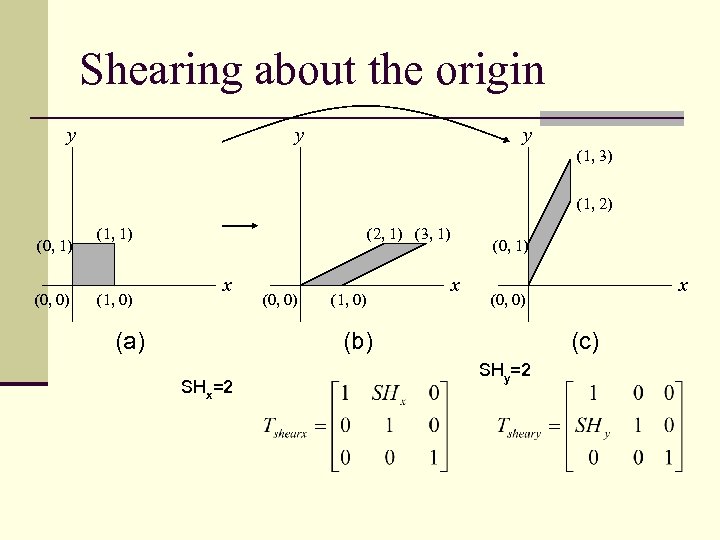Shearing about the origin y y y (1, 3) (1, 2) (0, 1) (0, 0) (1, 1) (1, 0) (2, 1) (3, 1) x (a) (0, 0) (1, 0) (0, 1) x (0, 0) (b) SHx=2 x (c) SHy=2

Shearing about the a reference point ( xr, yr)

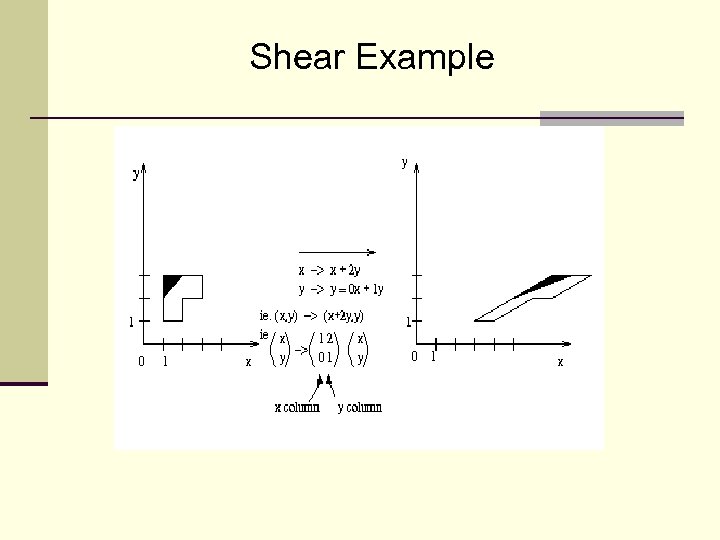Shear Example