Computer and Computational Problems J Kozánek Institute of

Computer and Computational Problems J. Kozánek Institute of Thermomechanics, Academy of Sciences, v. v. i. Department D 3 - Dynamics and Vibrations

Informatics, Hardware, Software, Algorithms, Programmable computer, Scientific computations, Technical calculations, Floating point arithmetic, Machine languages - machine code, Low and high - level programming languages, MATLAB, Linear equations. Matrices and vectors, Matrix zero, Numerical non-stability – condition numbetr, quadratic equation , Limited computer capacity - factorials

Experience and practice Learning Universatility , modeling theory and mathematics

Computer , Informatics analog, digital Ordinary digital computer : computer case, motherboard, processor, RAM, bus, graphics card, sound card, network card, hard disk, power supply, monitor, keyboard, mouse, touch screen input and output devices (printer, scanner, portable memory. . . ) hardware, software (programming, code) Scientific computing , algorithm, programming language and software

Characteristics of the computer ( scientific computing ) 1. Speed and accuracy (processor, math coprocessor ) FLOPS - FLoating-point OPerations per Second Desktop calculator has a capacity of only a few units FLOPS Year Supercomputer Peak speed Location 2013 NUDT Tianhe-2 33 PFLOPS Guangzhou, China 2012 Cray Titan 17 PFLOPS Oak Ridge, USA 2012 IBM Sequoia 17 PFLOPS Livermore, USA 2011 Fujitsu K comp. 10 PFLOPS Kobe, Japan 2. Operational memory (up to 128 GB), baud rate

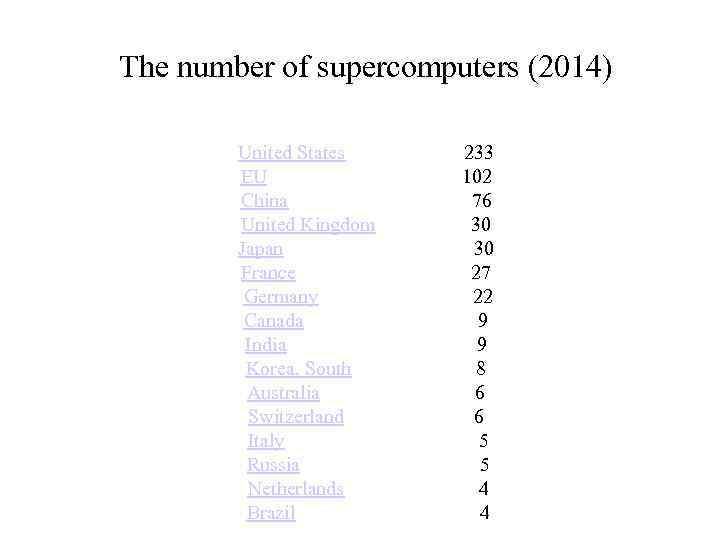
The number of supercomputers (2014) United States 233 EU 102 China 76 United Kingdom 30 Japan 30 France 27 Germany 22 Canada 9 India 9 Korea, South 8 Australia 6 Switzerland 6 Italy 5 Russia 5 Netherlands 4 Brazil 4

Prefix 1015 peta P biliard 1 000 000 000 PJ – petajoule 1012 tera T bilion 1 000 000 TW – terawatt 109 giga G milliard 1 000 000 GHz – gigahertz 106 mega M milion 1 000 Me. V–megaelenktronvolt 103 kilo k tisíc 1 000 kg – kilogram 102 hekto h sto 100 h. Pa – hektopascal 101 deka da deset 10 dag – dekagram

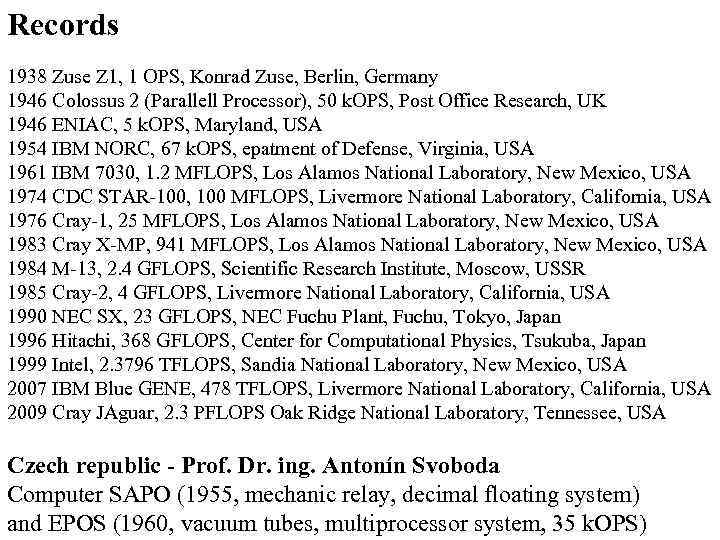
Records 1938 Zuse Z 1, 1 OPS, Konrad Zuse, Berlin, Germany 1946 Colossus 2 (Parallell Processor), 50 k. OPS, Post Office Research, UK 1946 ENIAC, 5 k. OPS, Maryland, USA 1954 IBM NORC, 67 k. OPS, epatment of Defense, Virginia, USA 1961 IBM 7030, 1. 2 MFLOPS, Los Alamos National Laboratory, New Mexico, USA 1974 CDC STAR-100, 100 MFLOPS, Livermore National Laboratory, California, USA 1976 Cray-1, 25 MFLOPS, Los Alamos National Laboratory, New Mexico, USA 1983 Cray X-MP, 941 MFLOPS, Los Alamos National Laboratory, New Mexico, USA 1984 M-13, 2. 4 GFLOPS, Scientific Research Institute, Moscow, USSR 1985 Cray-2, 4 GFLOPS, Livermore National Laboratory, California, USA 1990 NEC SX, 23 GFLOPS, NEC Fuchu Plant, Fuchu, Tokyo, Japan 1996 Hitachi, 368 GFLOPS, Center for Computational Physics, Tsukuba, Japan 1999 Intel, 2. 3796 TFLOPS, Sandia National Laboratory, New Mexico, USA 2007 IBM Blue GENE, 478 TFLOPS, Livermore National Laboratory, California, USA 2009 Cray JAguar, 2. 3 PFLOPS Oak Ridge National Laboratory, Tennessee, USA Czech republic - Prof. Dr. ing. Antonín Svoboda Computer SAPO (1955, mechanic relay, decimal floating system) and EPOS (1960, vacuum tubes, multiprocessor system, 35 k. OPS)

Procesors (CPU – Central Processing Unit) Intel, Motorola, AMD, SUN, DEC Alpha (4 – 64 bit) PC XT 8086, 8088, 80186), PC AT (80286, 80386, 80486, PENTIUM, INTEL Core. . ) Processor Speed (until 3 GHz) cache memory in CPU ( until 12 MB) Parallel processors (until 65000)

Number of significant digits of numbers with floating point significant digits × baseexponent IEEE 754 binary formats (optimal rounding , multiplication and division , complex numbers )

Natural numbers ( " number " - "the smallest infinity “ (Alef 0) Prime numbers 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541

Real numbers („number of real numbers“ – „infinity” ( Alef 1) Complex numbers Numbers: natural, whole numbers, rational , irrational , algebraic , transcendentní (Ludolfovo number , Euler number e) Note about the number of significant figures : a) Change in 7 th place after the decimal point causes an error of about 1 meter circle with a radius smaller than the radius of the earth (6500 km) b ) Question: When a circle of length of major terrestrial parallels extend about 1 m, how much will increase the radius ?

Pizza theorem In elementary geometry, the pizza theorem states the equality of two areas that arise when one partitions a disk in a certain way. Let p be an interior point of the disk, and let n be a number that is divisible by four and greater than or equal to eight. Form n sectors of the disk with equal angles by choosing an arbitrary line through p, rotating the line n/2 − 1 times by an angle of 2π/n radians slicing the disk on each of the resulting n/2 lines. Number the sectors consecutively in a clockwise or anti-clockwise fashion. Then the pizza theorem states that: The sum of the areas of the odd numbered sectors equals the sum of the areas of the even numbered sectors (Upton 1968).

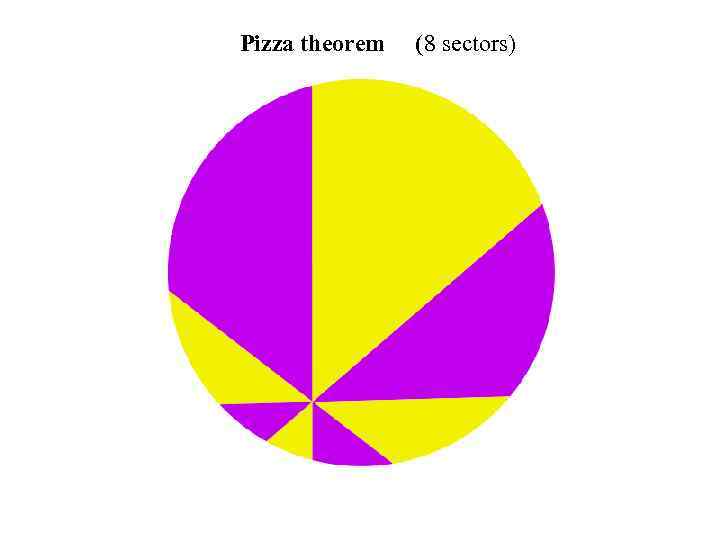
Pizza theorem (8 sectors)

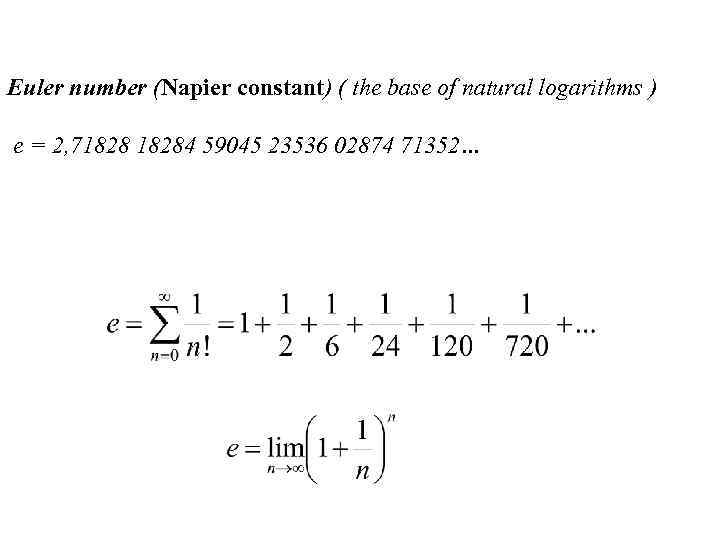
Euler number (Napier constant) ( the base of natural logarithms ) e = 2, 718284 59045 23536 02874 71352…

Euler (Euler-Mascheroni) constant, (rational? , irrational? )

Programming codes (languages) Machine code Assembler ALGOL, FORTRAN BASIC C, C++ COBOL PASCAL ADA JAVA Auto. CAD MATLAB MATHEMATICA, MAPLE, REDUCE

Programming in machine code - CPU Intel, instructions, data

Assembler (MS-DOS) A SEGMENT ASSUME CS: A, DS: A ORG 100 H START: MOV AH, 9 MOV DX, OFFSET TEXT INT 21 H MOV DL, '$' MOV AH, 2 INT 21 H INT 20 H TEXT DB 'THIS PROGRAM', 13, 10, ‘CAN WRITE I $' A ENDS END START

Pascal: begin writeln('THIS PROGRAM'); writeln(‘CAN WRITE I $'); end Matlab: ´THIS PROGRAM CAN WRITE I´ ´ 100 rows in FORTRAN code ----- 10 rows in MATLAB´

(Basic code): The example of simple code – the straight line fits measured points 10 REM FITTING OF THE POINTS BY LINE Y=A+BX 20 REM LEAST SQUARES METHOD 30 PRINT “HOW MUCH POINTS WILL BE ENTERED (3 -100)? " 40 INPUT N 41 45 IF N<3 THEN 30 42 46 IF N>100 THEN 30 50 REM THE INITIAL STATE VARIABLES 51 52 LET P 1=0 52 54 LET P 2=0 53 56 LET P 3=0 54 58 LET P 4=0 60 REM COORDINATES READING AND ADDITION 70 FOR I=1 TO N 80 PRINT I; ". PAIRS X, Y: "; 90 INPUT X, Y 100 LET P 1=P 1+X 110 LET P 2=P 2+Y 120 LET P 3=P 3+X*Y 130 LET P 4=P 4+X^2 140 NEXT I 150 REM CALCULATION OF THE REGRESSION COEFFICIENTS 160 LET B=(P 3 -P 1*P 2/N)/(P 4 -P 1^2/N) 170 LET A=(P 2 -P 1*B)/N 180 IF(B<0 THEN 186 182 LET Z$="-" 184 GOTO 190 186 LET Z$="+" 190 PRINT 200 PRINT “THE EQUATION OF THE LINE IS Y="A; Z$; ABS(B); "X" 210 PRINT

MATLAB code function [a, b]=regression(x, y) % % Regression of the line y = a + b*x % % Input: vectors x, y (dimension, length N) % Output: regression coefficients a, b % N=length(x); z=[ones(N, 1), x]y a=z(1); b=z(2);

MATLAB (friendly programming environment and optimal - reliable and fast numerical programs) 1980 (FORTRAN), 1985 (C++) PC XT (8086, 8088, 80186) PC AT (80286, 80386, 80486, PENTIUM, …) Workstation WINDOWS (1993), UNIX, LINUX MATLAB + TOOLBOX Optimization, control, signal processing, statistics, identification, fuzzy programming, image processing, finite element method, symbolic programming ( MAPLE ), neural networks, SIMULINK (simulation experiments)

Čísla v MATLABu Largest natural number = milliard (billion) = Smallest integer = Largest real number = The smallest positive real number = 'Relative accuracy of the calculations' , the number of significant digits ( double precision) eps =

Linear equation

2 linear equations with 2 unknowns no solution

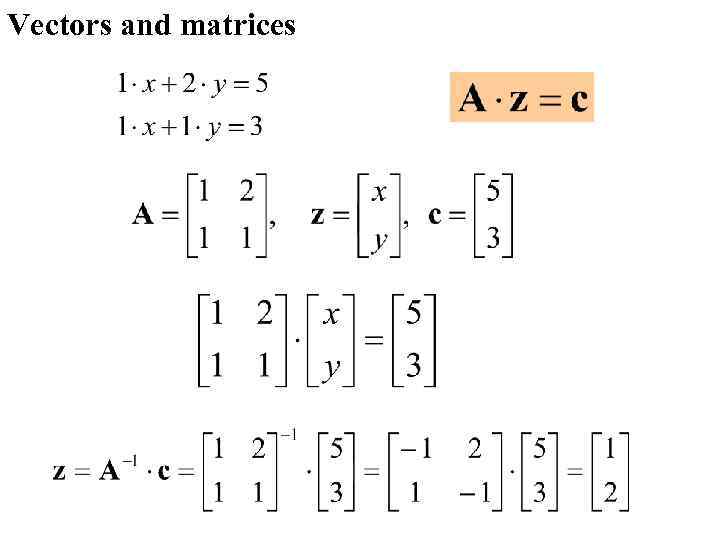
Vectors and matrices

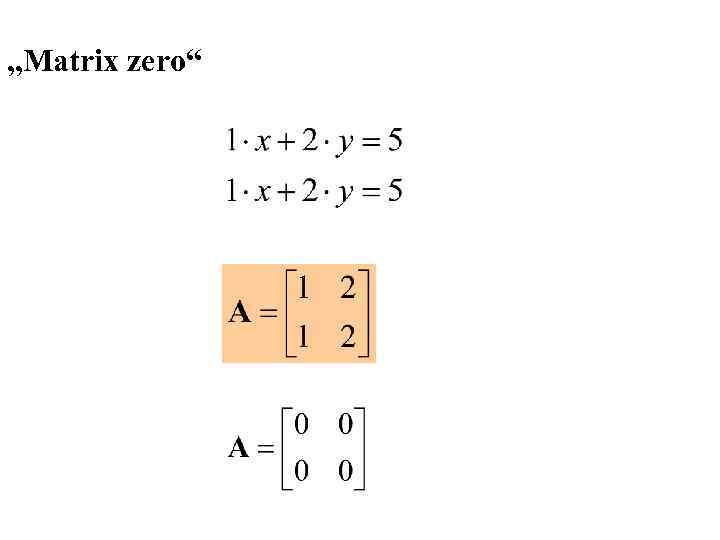
„Matrix zero“

Numerical instability in solving quadratic equations and the solution

The presumed computer working with 10 significant digits and exactly Classical solution Modified solution

„Commercial analysis“ of the solution of the quadratic equation Difference and the ratio is more expensive than the sum and product

Computer Performance Power of the man (with a simple calculator) for counting. For example for the man can in real time executes operations. Computer: for can executes operací. The limit of the applicability of computers Permutace The question: How large must be a number n that I could not on my computer performs mathematical operations ?

My notebook (INTEL Pentium 1, 7 GHz, 500 MB RAM) performs during 1 sec operations min = 60 sec hour = 60 minutes day = 24 hours year = 365 days 1 century = sec = mathematical operations CRAY Jaguar = 2, 3 PFLOPS = operations /sec 1 century = operací

Fundamental mathematical problems in Linear algebra System of linear equations Eigenvalue problem Quadratic eigenvalue problem Singular decomposition where

A general system of m linear equations with n unknowns can be written as

Decompositions related to solving systems of linear equations Decomposition: , where L is lower triangular and U is upper triangular LDU decomposition Cholesky decomposition square, symmetric, positive definite matrix QR decomposition m-by-n matrix where Q is an orthogonal matrix of size m-by-m, and R is an upper triangular matrix of size m-by-n

The QR decomposition provides an alternative way of solving the system of equations without inverting the matrix A. The fact that Q is orthogonal means that , so that is equivalent to , which is easier to solve since R is triangular.

Eigendecomposition (spectral decomposition) • Applicable to: square matrix A with distinct eigenvectors (not necessarily distinct eigenvalues). • Decomposition: • where D is a diagonal matrix formed from the eigenvalues of A, and the columns of V are the corresponding eigenvectors of A. The decomposition (if A is real-symmetric) Jordan decomposition

QZ decomposition Q and Z are unitary matrices, the H superscript represents conjugate transpose, and S and T are upper triangular matrices. Takagi's factorization for: square, complex, symmetric matrix A.

Matrix polar decomposition The polar decomposition of a square complex matrix A is a matrix decomposition of the form where U is a unitary matrix and P is a positive-semidefinite Hermitian matrix.

2 × 2 matrices - Determinants The area of the parallelogram is the absolute value of the determinant of the matrix formed by the vectors representing the parallelogram's sides. The determinant of a 2 × 2 matrix is defined by 3 × 3 matrices - Determinants The determinant of a 3 × 3 matrix is defined by

Singular decomposition The rectangular matrix Non-negative numbers are singular valalues of A – by the definition are the roots of the eigenvalues of matrices or Matrices W or U are their modal matrices. Singular value decomposition is among the most stable numerical algorithms and can be used to decompose of any matrix. Singular numbers define the numerical rank of a matrix A (the number of singular values larger than the small ).

Moore-Penrose pseudoinversion matrix can be define by singular decomposition The least squares problem solution

The conditioning of the linear algebra problems We say that the problem is well conditioned , if the "small change" Db of the vector b causes a "small change" Dx of the solution x. The condition number we can define as For , the problem is very well conditioned, the larger will be k, the problem will be badly conditioned. where we use the so called spectral norm of matrix For small order matrix the condition number is inversely proportional to the determinant of the matrix. But generally, there are very well conditioned matrices with small determinants and very badly conditioned matrices with determinant equal to 1.