Computational nc RNA gene finding nc RNA structure

Computational nc. RNA gene finding nc. RNA structure prediction (& computational nc. RNA gene finding) (& nc. RNA structure prediction) Liming Cai (BINF 8210@UGA, Fall 2010)

Non-coding RNAs • Functions other than coding proteins, e. g. , structural, catalytic, and regulatory factors functional RNAs = nc. RNAs + UTR motifs • (-) No strong statistical features, such as ORFs, or polyadenylated, demonstrated in coding genes • (+) Transcribed nc. RNA molecules can fold into secondary and tertiary structures (more conserved than sequences)

Sources of nc. RNAs • Non-coding RNA genes encode RNAs, e. g. , mi. RNAs, rox 1 and rox 2 RNAs in male Drosophila melanogaster. • In introns and intergenic regions, e. g. , sno. RNAs • In 5’ and 3’ UTRs, e. g. , regulatory motifs (functional RNAs)

Functions of nc. RNAs • r. RNAs and t. RNAs • RNA maturation: sn. RNA in recognizing splicing sites • RNA modification: sno. RNA converting uridine to pseudo-uridine • Regulation of gene expression and translation: e. g. , mi. RNAs • DNA replication: e. g. , telomerase RNAs - template for addition of telomeric repeats • Etc.

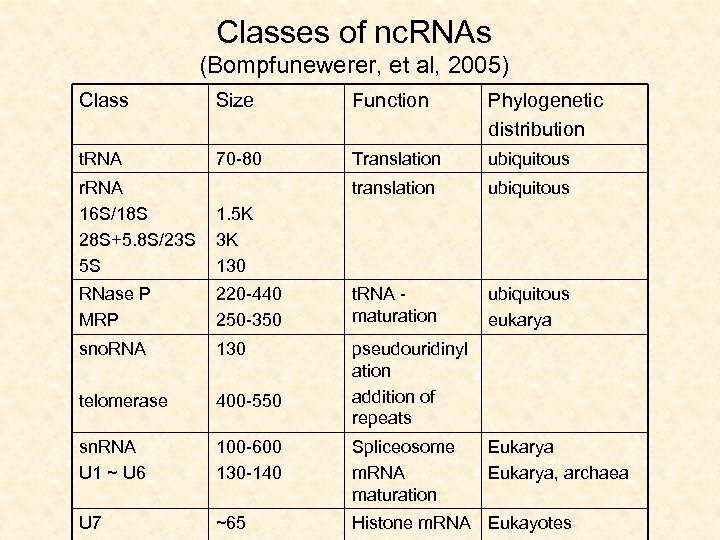Classes of nc. RNAs (Bompfunewerer, et al, 2005) Class Size Function Phylogenetic distribution t. RNA 70 -80 Translation ubiquitous translation ubiquitous eukarya r. RNA 16 S/18 S 28 S+5. 8 S/23 S 5 S 1. 5 K 3 K 130 RNase P MRP 220 -440 250 -350 t. RNA maturation sno. RNA 130 telomerase 400 -550 pseudouridinyl ation addition of repeats sn. RNA U 1 ~ U 6 100 -600 130 -140 Spliceosome m. RNA maturation U 7 ~65 Histone m. RNA Eukayotes Eukarya, archaea

Some nc. RNAs databases • Rfam (280, 000 regions of 379 families) • NONCODE (109 transitional classes and 9 groups) • RNAdb (800 mammalian nc. RNAs, excluding t. RNAs, r. RNAs and sn. RNAs) • Arabidposis small RNA Project (ASRP) • Etc.

nc. RNA gene finding strategies 1. Computational predictive methods 2. c. DNA cloning to enrich nc. RNAs 3. Detecting new transcripts with oligonucleotide microarrays

nc. RNA gene finding: a computational challenge • nc. RNA genes do not have significant statistical signals • large in number • diverse, 20 nts to 22, 000 nts - Not sure what to look for - Computationally intensive - Simply no good method - Methods compromising accuracy

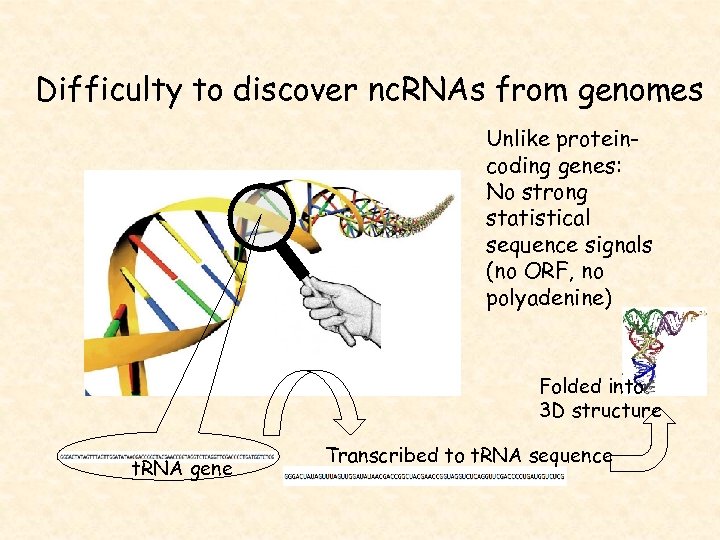Difficulty to discover nc. RNAs from genomes Unlike proteincoding genes: No strong statistical sequence signals (no ORF, no polyadenine) Folded into 3 D structure t. RNA gene Transcribed to t. RNA sequence

Computational nc. RNA gene finding methods • Specific (custom-designed) nc. RNA search and annotation (e. g. , t. RNAscan, methylattion-guide sno. RNA, mi. RNA, tm. RNA) • Reconfigurable search systems (e. g. , Infernal, ERPIN, RNATOPS, Fast. R) – mechanism to profile the target nc. RNA (structure) - need training data • De novo nc. RNA gene detection with – base composition (e. g. , G+C %) – structure fold (e. g. , RNAz) • Comparative analysis (e. g. , QRNA, Evol. Fold) - consensus structure • nc. RNA “holy grail” ?

Review literature in computational nc. RNA gene finding and annotation • A. Laederach (2007) Informatics challenges in Structural RNA, Brief Bioinformatics 8(5) 294 -303. • S. Eddy (2001) Non-coding RNA genes and modern RNA world, Nature Reviews Genetics, 2(12), 919 -929. • S. Griffiths-Jones (2007) Annotating noncoding RNA genes, Annual Rev. Genomics & Human Genetics, 8: 279 -298. • Machado-Lima et al (2008) Computational methods in noncoding RNA research, Mathematical Biology, 56: 15 -49.

506 mi. RNAs Comparison between NUPACK and Triple 499 t. RNAs Comparison between NUPACK and Triple Data were from Bonnet et al, 2004

499 t. RNA Comparisons between HG, Triple, NUPACK 499 t. RNA Comparisons between HG and NUPACK Data were from Bonnet et al, 2004

What are in this lecture? • RNA secondary structure prediction 1. ab initio structure prediction 2. consensus structure prediction 3. structural model-based prediction but why just secondary structure? [t. RNA unfolding pathway] [Doudna, et al, 1999]

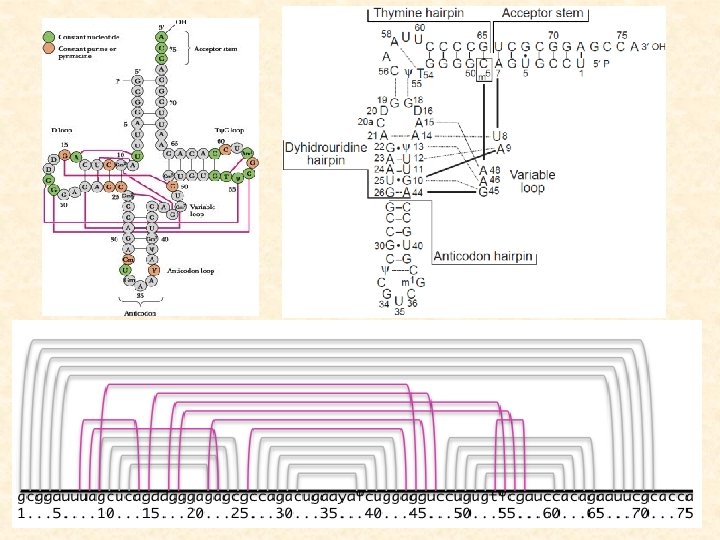
• Tertiary structure: Less understood non-canonical interactions Only a small number of resolved structures • Secondary structure: (Well understood) canonical base pairs Scaffolding tertiary structure Well studied, many known structures Measuring nc. RNA secondary structure may be a feasible solution for nc. RNA gene finding

What else are in this lecture? • nc. RNA gene finding and annotation 4. Structural profile-based nc. RNA gene annotation 5. comparative analysis based nc. RNA gene finding 6. ab initio nc. RNA gene detection

Base pairings of RNAs • Base pairings allow RNA to fold Watson-Crick base pairs: A-U, C-G Wobble pair G-U called canonical pairs for secondary structure Note: all 16 (including non-canonical) base pairs are possible for RNA tertiary structure

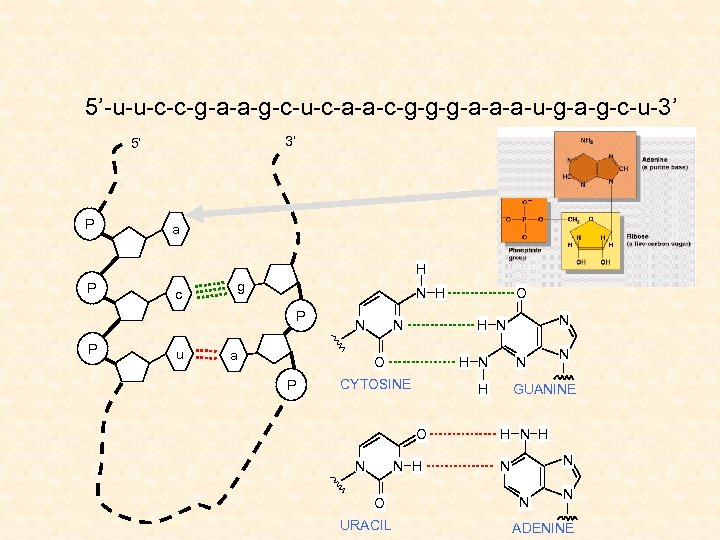5’-u-u-c-c-g-a-a-g-c-u-c-a-a-c-g-g-g-a-a-a-u-g-a-g-c-u-3’ 3’ 5’ P a H P c g N H P P u N a N H N CYTOSINE N H O URACIL N H O N N H N O P O N GUANINE H N N N N ADENINE

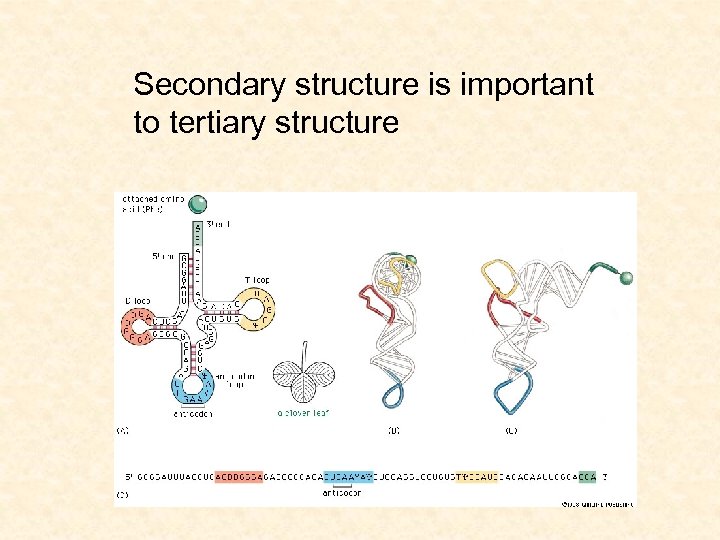Secondary structure is important to tertiary structure

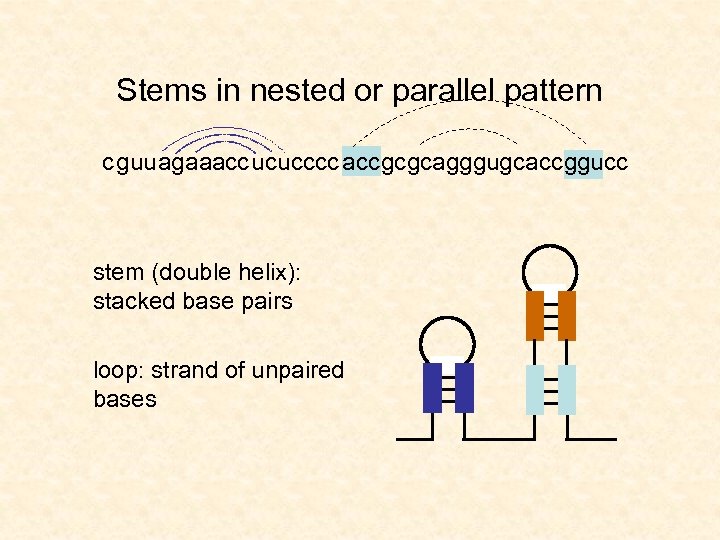Stems in nested or parallel pattern c guu agaaacc ucu cccc acc gc gcagggugc acc ggucc stem (double helix): stacked base pairs loop: strand of unpaired bases

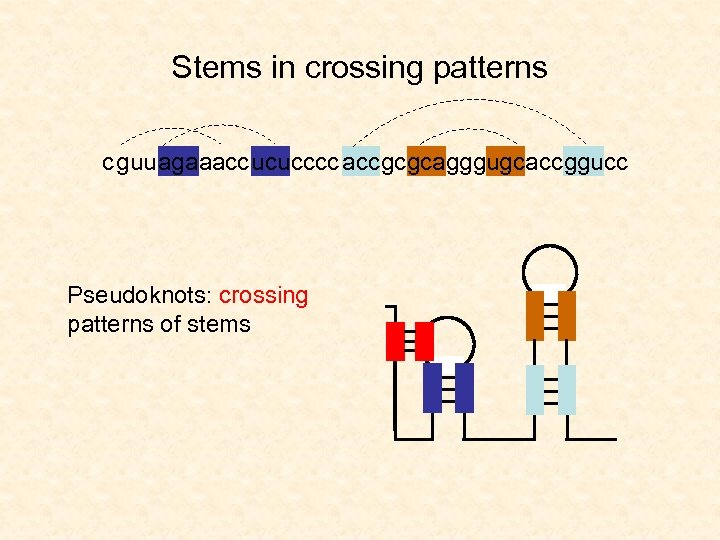Stems in crossing patterns c guu agaaacc ucu cccc acc gc gcagggugcacc ggucc Pseudoknots: crossing patterns of stems

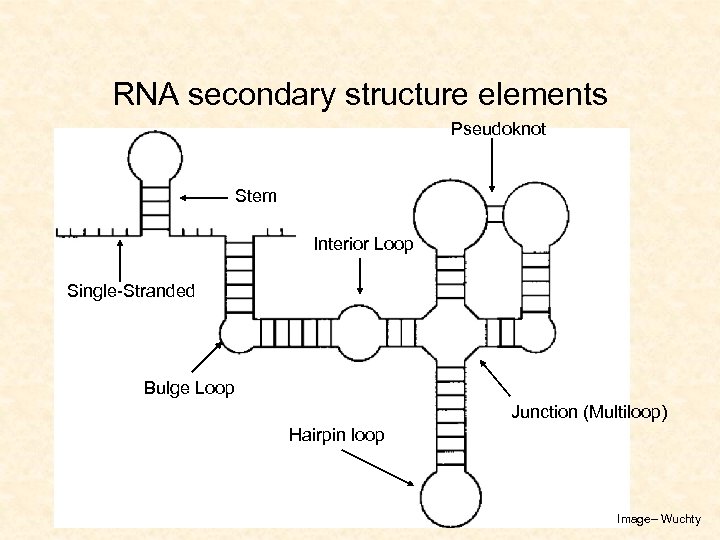RNA secondary structure elements Pseudoknot Stem Interior Loop Single-Stranded Bulge Loop Junction (Multiloop) Hairpin loop Image– Wuchty

RNA stem-loop (pseudoknot-free) structure example

RNA secondary structure prediction 1. ab inito structure prediction to predict the structure of a single sequence 2. Consensus structure prediction to predict the structure shared by more than one sequences 3. Statistical model-based prediction and alignment to search for desirable structures on genomes or data bases

1. ab initio structure prediction • Hydrogen bonds consume energy contained in the molecule. • The smaller the free energy is, the more stable the structure folded.

ab initio structure prediction (cont’) • Consider only canonical base pairs A-U, C-G, and G-U. Base pairings reduce the amount of free energy contained in the molecule. • Maximizing the number of base pairs would minimize the free energy in the molecule. (Only an approximate model)

ab initio structure prediction (cont’) • But how to count? An RNA could be very long; there may be many possible ways that base pairs can be formed: e. g. , ……ACGGUACGUC…. . conflicting pairs A-U, A-U G-C, G-C etc. Even the number of non-conflicting combinations of base pairs is exponentially large.

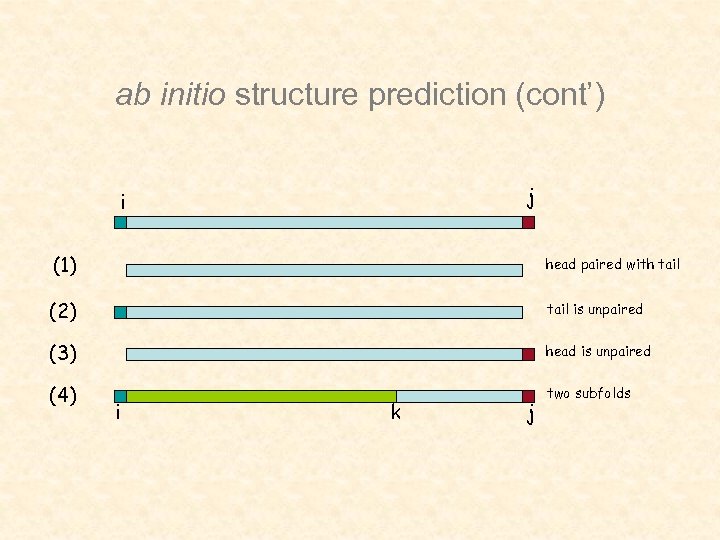ab initio structure prediction (cont’) j i (1) head paired with tail (2) tail is unpaired (3) head is unpaired (4) two subfolds i k j

looking at shorter (e. g. , very short) subsequences in a long sequence ACGGU…ACGUC • For subsequences of length 1, A, C, G, G, U, …, A, C, G, U, C #of base pairs 0, 0, 0, …, 0, 0, 0 • For subsequences of length 2, AC, CG, GU, …, AC, CG, GU, UC # 0, 1, …, 0, 1, 0 • For subsequence of length 3, ACG, CGG, GGU, …, UAC, ACG, CGU, GUC, UUC ? : e. g. , GUC (1) G-C + U --> 1+0 =1 head-tail (2) G + UC --> 0+0 =0 head unpaired (3) GU + C tail unpaired --> 1+0 =1 (4) GU + C --> 1+0 =1 split (5) G + UC --> 0+0 =0 split

examine a little longer sequence …. . ACGGUACGU…. . i j ==> max of {cases 1, 2, 3, 4} 1. Head-tail paired, count = 1 + max count in subsequence CGGUACG i+1 j-1 2. Head unpaired, count = max count in subsequence CGGUACGU i+1 j • Tail unpaired, count = max count in subsequence ACGGUACG i j-1 • Split (why needed and where to split ? ) ACGGUACGU when k=i+2 i j ==> ACG + GUACGU <---- k ---> count = max count in ACG + max count in GUACGU

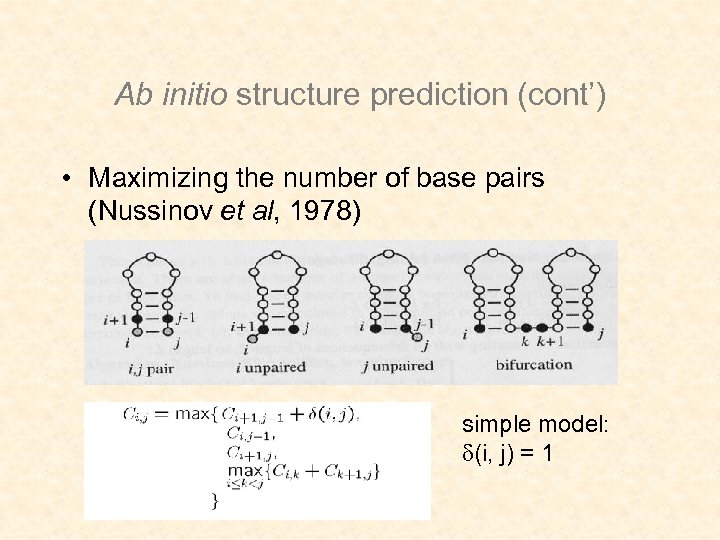Ab initio structure prediction (cont’) • Maximizing the number of base pairs (Nussinov et al, 1978) simple model: (i, j) = 1

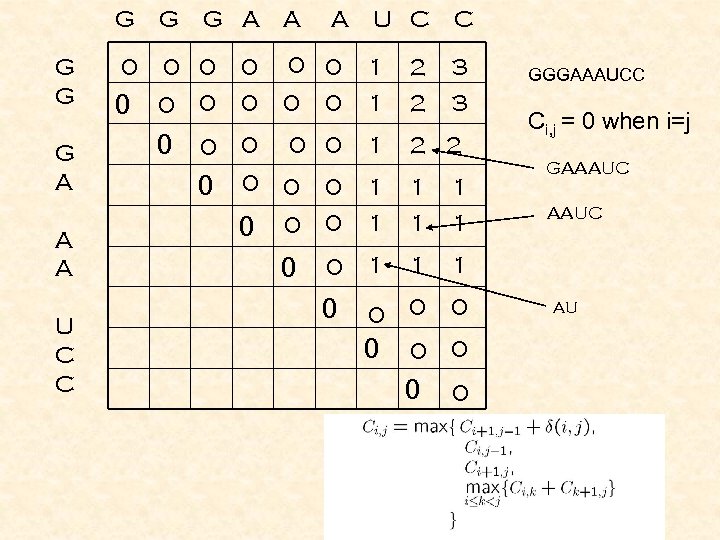G G G A A A U C C 0 0 G A U C C 0 0 1 1 2 2 3 3 0 0 0 1 2 2 0 0 0 0 A 1 1 1 0 Ci, j = 0 when i=j GAAAUC 1 0 0 GGGAAAUCC 0 0 0 AAUC AU

Example 2: ACGGUU subsequence of length 0: empty sequence, 0 subsequences of length 1: A, C, G, G, U, U 0 0 0 0 subsequences of length 2: AC, CG, GU, UU 0 1 1 0 0 subsequences of length 3: ACG, CGG, GGU, GUU 1 1 1 Subsequences of length 4: ACGG, CGGU, GGUU 1 2 2 Subsequences of length 5: ACGGU, CGGUU 2 2 subsequence of length 6: ACGGUU 3 pairs pairs

Prediction Algorithm Web Server • http: //frontend. bioinfo. rpi. edu/applications/mfold/cgi-bin/rna-form 1. cgi • Sample sequence: (1) t. RNA GGGGUCAUAGCUCAGUUGGUAGAGCGCUACAAUGGCAUUGUAGAGGUCAGCGG UUCGAUCCCGCUUGGCUCCACCA (2) a part of tm. RNA CCUCUCUCCCUAGCCUCCGCUCUUAGGACGGGGAUCAAGAGAGGUCA AACCCAAAAGAGA • Simple matrix, • simple matrix with G-U pair • Complex matrix Rfam database: http: //www. sanger. ac. uk/Software/Rfam/

Thermodynamic energy based structure prediction • Energy minimization algorithm predicts the correct secondary structure by minimizing the free energy ( G) • G calculated as sum of individual contributions of: – loops – base pairs – secondary structure elements

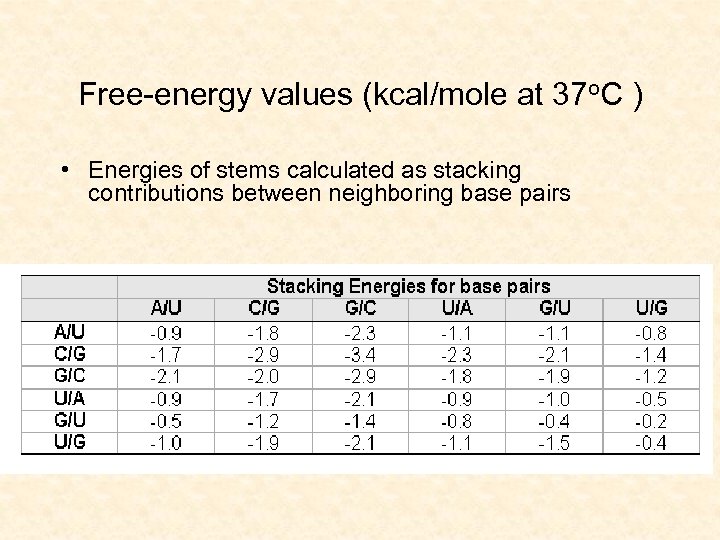Free-energy values (kcal/mole at 37 o. C ) • Energies of stems calculated as stacking contributions between neighboring base pairs

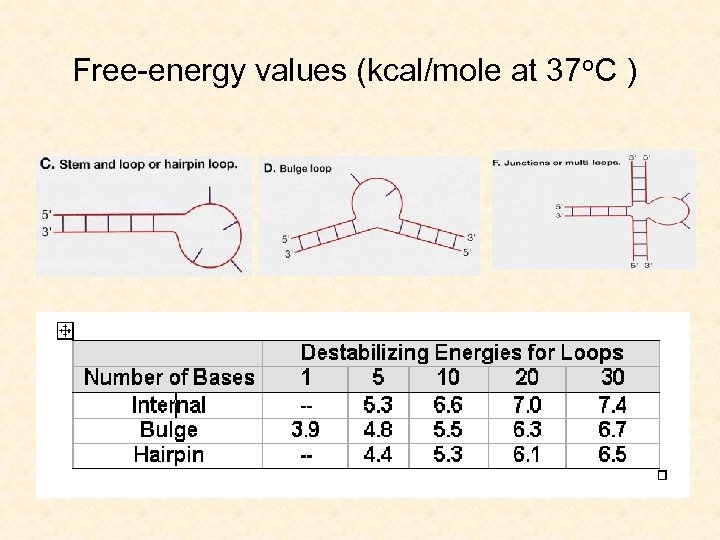Free-energy values (kcal/mole at 37 o. C )

Zuker’s algorithm MFOLD: computing loop dependent energies

Assumptions in such algorithms • Most likely structure corresponds to energetically most stable structure • Energy associated with any position is only influenced by local sequence and structure • Structure formed does not produce pseudoknots

RNA structure prediction web servers • MFOLD http: //www. bioinfo. rpi. edu/applications/mfold/rna/form 1. cgi • RNAfold ( a part of Vienna Package) http: //rna. tbi. univie. ac. at/cgi-bin/RNAfold. cgi Examples: GCTTACGACCATATCACGTTGAATGCACGC CATCCCGTCCGATCTGGCAAGTTAAGCAAC GTTGAGTCCAGTTAGTACTTGGATCGGAGA CGGCCTGGGAATCCTGGATGTTGTAAGCT

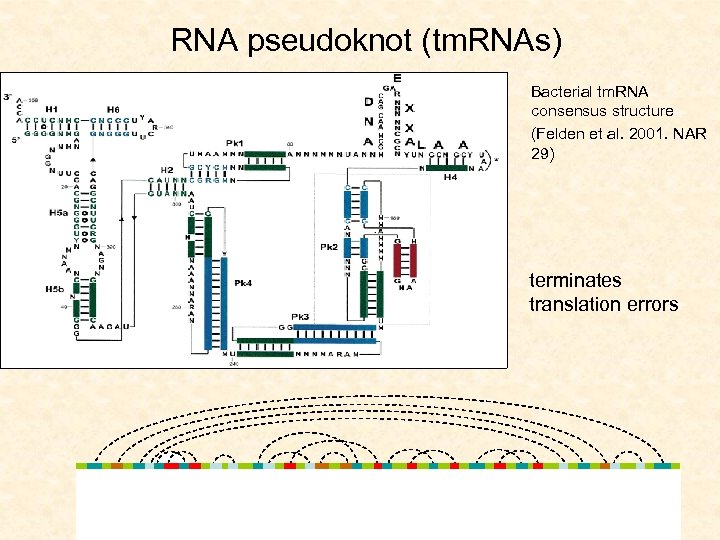RNA pseudoknot (tm. RNAs) Bacterial tm. RNA consensus structure (Felden et al. 2001. NAR 29) terminates translation errors

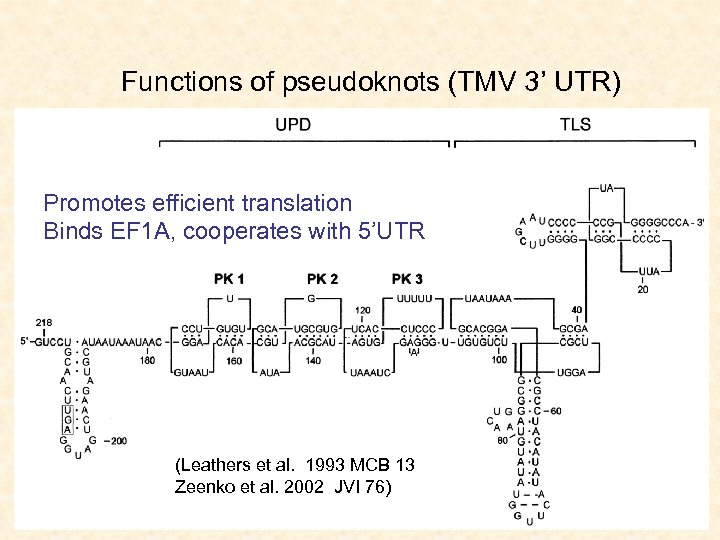Functions of pseudoknots (TMV 3’ UTR) Promotes efficient translation Binds EF 1 A, cooperates with 5’UTR (Leathers et al. 1993 MCB 13 Zeenko et al. 2002 JVI 76)

Pseudoknots drastically increase computational complexity

RNA pseudoknot prediction web servers • Pknots-RG: http: //bibiserv. techfak. uni-bielefeld. de/pknotsrg/ • Pknots-RE (the first pseudoknot prediction algorithm) • Kinefold: http: //kinefold. curie. fr/cgi-bin/form. pl • ILM http: //cic. cs. wustl. edu/RNA/

Computational complexity issues • • Pseudoknot-free structures: O(n 3) CUP time Pseudoknots: NP-hard, restricted cases O(n 5) Heuristics added: O(n 4) Difficult for search RNA structures in genomes

2. Consensus structure prediction Covariance fact for RNAs: Variations in RNA sequence maintain base-pairing patterns for secondary structures When a nucleotide in one base changes, the base it pairs to must also change to maintain the same structure

Structure alignments (example) CA G • C G • C AA G A C • G U • A A • U GA G A A G U G C A C U Query RNA structure A: structural homolog B: nonhomologous primary sequence alignment scoring: query: GGGGGCAACCCC A: AUCCGAAAGGAU B: CCUAGAAAGGAU | | | -6 | | | -6 structure + sequence alignment scoring: query: GGGGGCAACCCC A: AUCCGAAAGGAU B: CCUAGAAAGGAU | | |||||| +11 | | | -6

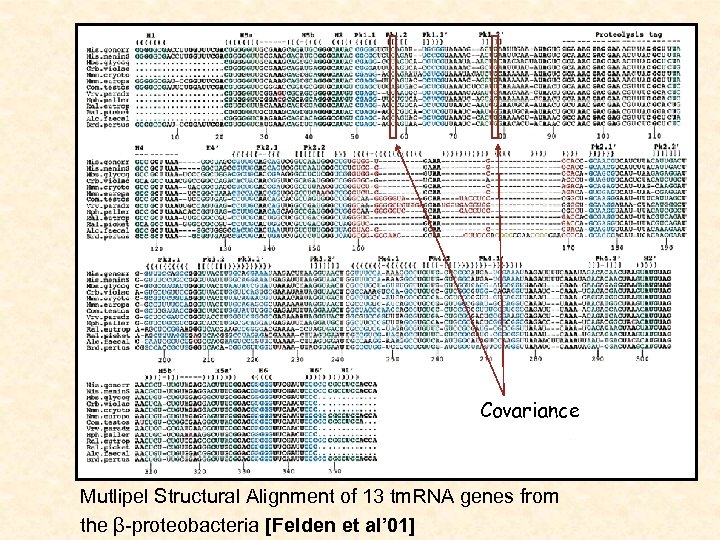Covariance Mutlipel Structural Alignment of 13 tm. RNA genes from the β-proteobacteria [Felden et al’ 01]

Dynamic programming approach • (Sankoff 1984) This can be regarded as running ‘two Nussinov algorithms at the same time’ to simultaneously fold two RNAs j i p q ‘the coordinated fold’ is found through computing Ci, j, p, q, needs: O(n 6) time for two sequences and O(n 3 k) for k seqs

Inferring structure by comparative sequence analysis • (1) calculate a multiple sequence alignment Requires sequences to be similar enough so that they can be initially aligned Sequences should be dissimilar enough for covarying substitutions to be detected

Inferring structure by comparative sequence analysis (cont’) • (2) compute Mutual Information fxi : frequency of a base x in column i • fxiyj : joint (pairwise) frequency of base pair x-y between columns i and j • If i and j are uncorrelated, mutual information is 0

Inferring structure by comparative sequence analysis (cont’) • (3) use mutual information Mi, j as pairing “energy” and treat the multiple alignment as a “generic” sequence • apply a Nussinov’s algorithm-like process to find the most likely common structure

Inferring consensus structure by a graphtheoretic approach (Con. RAN and RNASampler) • Identify all stems in every sequence, assigning each stem a vertex in the graph • Connect two stems in two different sequences with an edge if they are similar • Connect two stems in the same sequence with an edge if they do not conflict • The optimal consensus structure corresponds the maximum clique

Consensus structure prediction programs • Dynalign http: //rna. urmc. rochester. edu/dynalign. html • Foldalign http: //www. bioinf. au. dk/cgi-bin/webparser-1. 5. pl • Com. RNA http: //ural. wustl. edu/~yji/com. RNA/ • RNA sampler http: //ural. wustl. edu/~xingxu/RNASampler/index. html • Carnac http: //bioinfo. lifl. fr/RNA/carnac. php

3. Statistical model-based structure prediction and alignment • Extension from HMM to include mechanisms that can describe (long -distance) base pairings • Stochastic grammars can describe models defined by HMMs • Stochastic grammars can describe models not definable by HMMs

Stochastic context-free grammar • Covariance model (CM) [Eddy and Durbin’ 94] based on computational grammar systems M 2 a M’ 2 I 2 a I 2 M 3 D 2 I 2 D 2 M 3 M’ 2 D 3 I 2 D 3 D 2 D 3 A path in the HMM a derivation in the grammar

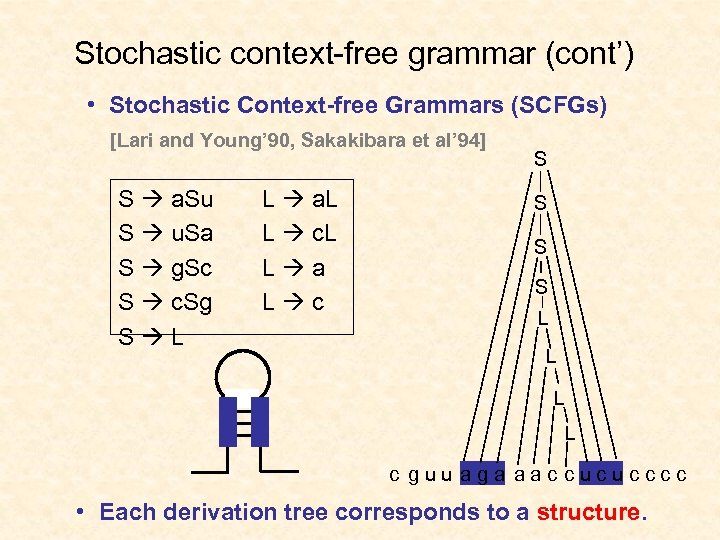Stochastic context-free grammar (cont’) • Stochastic Context-free Grammars (SCFGs) [Lari and Young’ 90, Sakakibara et al’ 94] S a. Su S u. Sa S g. Sc S c. Sg S L L a. L L c. L L a L c S S L L c g u u a g a a a c c u c c • Each derivation tree corresponds to a structure.

Stochastic context-free grammar (cont’) S a. Su S c. Sg ac. Sgu S g. Sc acc. Sggu S u. Sa accu. Saggu S a accu. SSaggu S c accug. Sc. Saggu S g accugg. Scc. Saggu S u accuggacc. Saggu S SS accuggaccc. Sgaggu accuggacccu. Sagaggu accuggacccuuagaggu 1. A CFG 2. A derivation of “accuggacccuuagaggu” 3. Corresponding structure

What to do with SCFGs ? • Structure prediction require the SCFG model to be flexible enough • Structure search require the model to be specific • Both need to do sequence-structure alignment

S a. Su S c. Sg S g. Sc S u. Sa S a. S S c. S S g. S S u. S Structure prediction with SCFG Probability parameter assignment: (1) Sum of probabilities of the same LHS =1 (2) Geometric distributions for loop and stem lengths (3) Parameters are obtained from training sequences with known structures S Sa S Sc S Sg S Su S a S c S g S u S SS Alignment score between model S and subsequence x[i. . j] is computed, when x[i]=a, x[j]=u C(S, i, j) = max { C(S, i+1, j-1)*P(S -> a. Su), C(S, i+1, j)*P(S -> a. S), C(S, I, j-1)*P(S -> Su), maxk { C(S, i, k)C(S, k+1, j)P(S->SS) }

S a. Su S c. Sg S g. Sc S u. Sa Web servers for RNA Structure prediction with SCFG S a. S S c. S S g. S S u. S S Sa Infernal: http: //infernal. janelia. org/ S Sc S Sg S Su S a S c S g S u S SS Pfold: (multiple sequence + SCFG) http: //www. daimi. au. dk/~compbio/rnafold/

• RNA secondary structure prediction 1. ab initio structure prediction 2. consensus structure prediction 3. structural (SCFG) model-based prediction • nc. RNA gene finding and annotation 4. profile-based nc. RNA gene annotation 5. comparative analysis based nc. RNA gene finding 6. ab initio nc. RNA gene prediction

4. Structure profile based RNA gene annotation Secondary structure alone is not sufficient for predicting nc. RNA genes, BUT it remains to be the best hope for an exploitable statistical signal To find RNA structures or genes, one can profile the structure to be searched. Often, SCFG is used as a modeling tool.

Structure profile based RNA gene annotation (cont’) • Search for a specific family RNAs (structures) • Need an effective mechanism to profile the family • Need a fast structure-sequence alignment algorithm

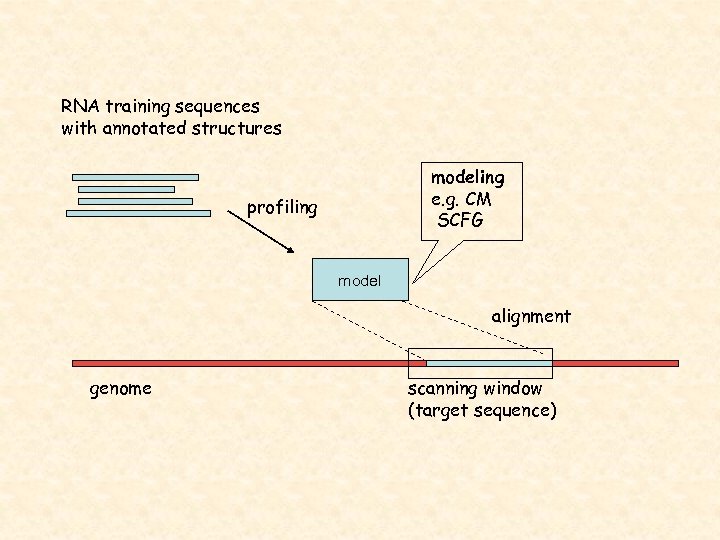RNA training sequences with annotated structures modeling e. g. CM SCFG profiling model alignment genome scanning window (target sequence)

• CM is a profile-SCFG, position-specific, very effective • Slow O(n 3 N)-time even for pseudoknot-free RNAs in genomes or large databases • Cannot handle pseudoknots • HMM based filtering to imprve speed • Examples: t. RNAscan-SE (http: //lowelab. ucsc. edu/t. RNAscan-SE/) infernal (http: //infernal. janelia. org/)

5. Comparative analysis based nc. RNA gene finding • Based on structure features of RNA • • Consider two or more genomes phylogenetically related Use sequence alignment tools (such as BLASTN) to find local alignment between the two Search with a sliding window Identify potential RNA fold within the window Computationally verify it to be putative RNA • • • QRNA (Eddy group, 2001) Evo. Fold (Haussler group, 2006) RNAz (Stadler group, 2005)

QRNA (Eddy et al, 2001) detecting nc. RNA genes with SCFGs given two aligned sequences, to test the pattern of substitutions observed in the pairwise alignment of two homologous sequences using a pair of SCFGs for nc. RNAs (compensatory mutations) a pair HMM for protein-coding genes (conserved regions) a pair HMM for other regions (random evolution)

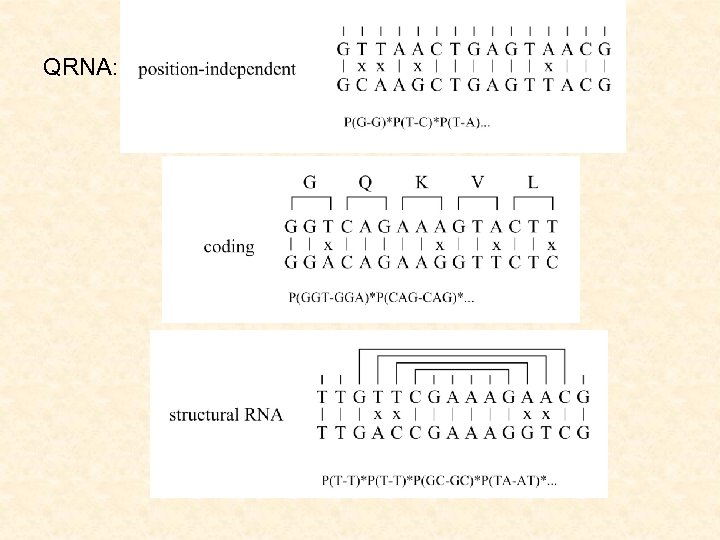QRNA:

Probability parameters

Other software to detect RNA genes based on comparative analysis • Evo. Fold multiple genomes use SCFG + phylogeny to predict consensus structure • RNAz multiple genomes predict the consensus fold compare energy of the fold to background energy

3. Ab initio prediction of nc. RNA genes • mainly based on base composition difference between real RNAs and the background, limited success. • Unsuccessful by simply predicting the structure of RNAs • Other methods?

Fold energy and fold certainty • Methods based on folding energy do not seem to work [just like structure prediction] • How do distinguish a real nc. RNA from random sequences that fold to the same structure by chance [both could have the same energy] • The difference seems to be the structure certainty • But how to compute structure certainty?

Fold certainty • For a real nc. RNA sequence: Base pairs contributing to the real fold should not be everywhere. ‘overall strength’ of base pairs contributing to other, false folds should be weak. • For a random sequence: either it does not fold or there is a low probability to form a certain fold

Fold certainty (cont’) • Compute Shannon entropy En(S) = ∑Pij log Pij where Pij is the probability for bases i and j to pair • Pij = (number of folds pair (i, j) is involved) / (number of folds) [simplified]

Fold certainty (cont’) • • We measured entropy Z-score of a real nc. RNA based on the entropies of its random counterparts But the entropy Z-score performance on different nc. RNAs is different mi. RNAs perform well while t. RNAs do not What happened?

Readings and projects in RNA informatics • www. uga. edu/RNA-Informatics/Readings • www. uga. edu/RNA-Informatics/Projects/project-details. html

What about pseudoknots?

Tree decomposition based search algorithms • Dynamic programming at the nucleotide level is time consuming • Very Slow, O(n 6 N)-time even for restricted pseudoknot categories • Pseudoknots are not very complex from graph -theoretic point of view

Tree decomposition based search algorithms (cont’s) • profile each stem with SCFG, connecting the two halves with an edge profile each loop with HMM, connect two ends of the loop with a directed edge Produce a mxied graph H for the structure • Preprocess target sequence with the profiles to obtain all potential candidates, construct a graph G for the sequence • Structure-sequence alignment corresponding finding an optimal subgraph in G isomorphic to H

Tree decomposition based search algorithms (cont’s) • H is decomposed as a tree representation • Fast alignment algorithm can be obtained O(kt Nn) where t is the tree width of H, usually small for pseudoknotted RNAs, k is a parameter, small also • Successful for RNA structures that belong to a well-defined family

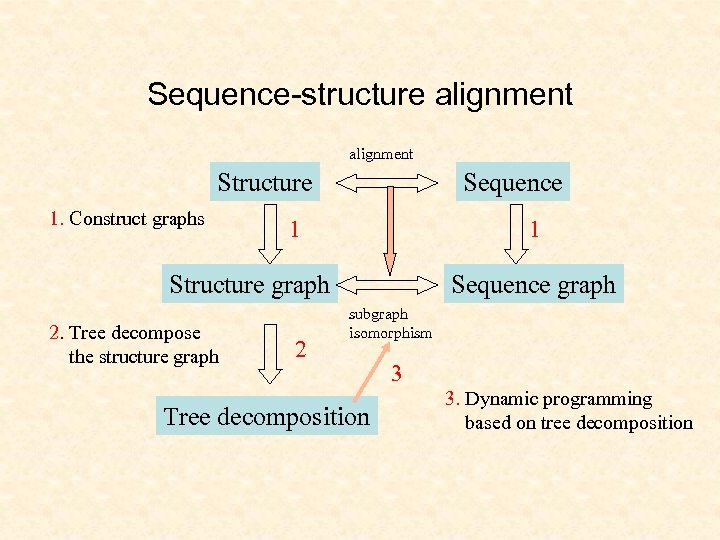Sequence-structure alignment Structure 1. Construct graphs Sequence 1 1 Structure graph 2. Tree decompose the structure graph 2 Sequence graph subgraph isomorphism Tree decomposition 3 3. Dynamic programming based on tree decomposition

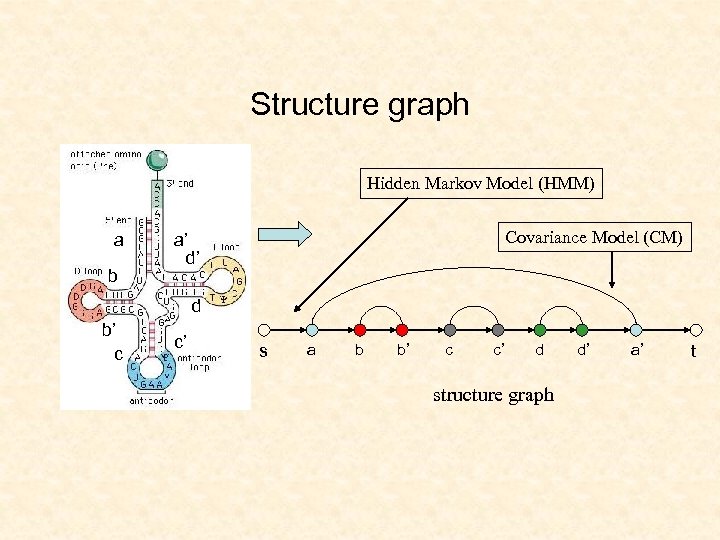Structure graph Hidden Markov Model (HMM) a b Covariance Model (CM) a’ d’ d b’ c c’ s a b b’ c c’ d structure graph d’ a’ t

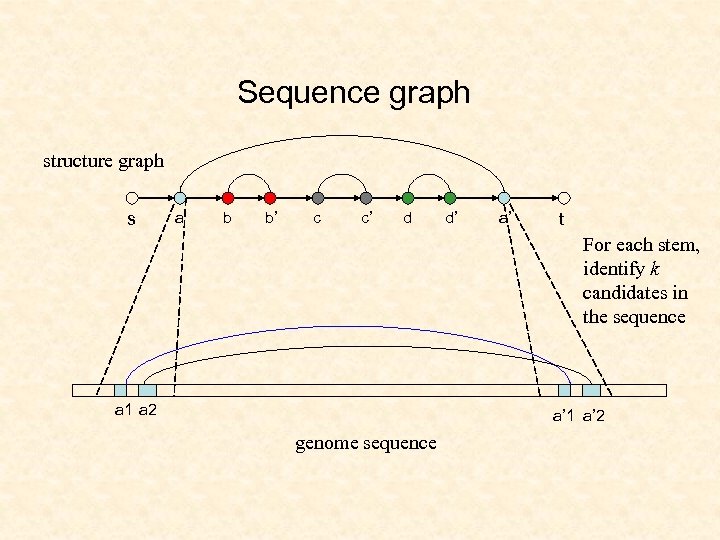Sequence graph structure graph s a b b’ c c’ d d’ a’ t For each stem, identify k candidates in the sequence a 1 a 2 a’ 1 a’ 2 genome sequence

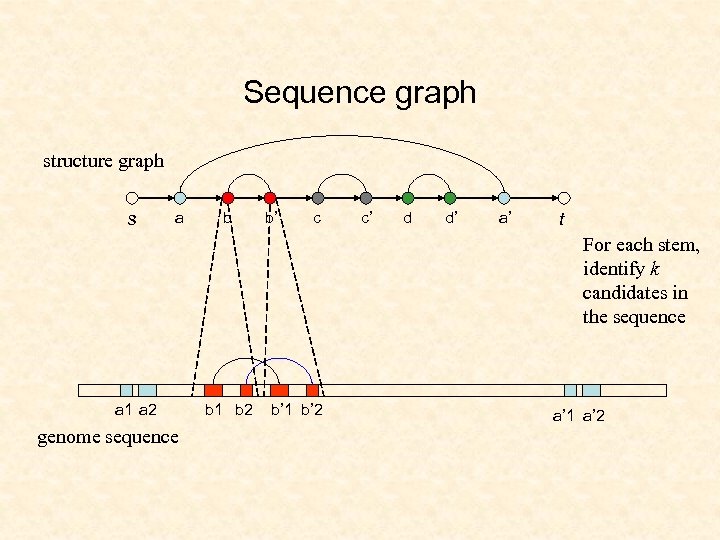Sequence graph structure graph s a b b’ c c’ d d’ a’ t For each stem, identify k candidates in the sequence a 1 a 2 genome sequence b 1 b 2 b’ 1 b’ 2 a’ 1 a’ 2

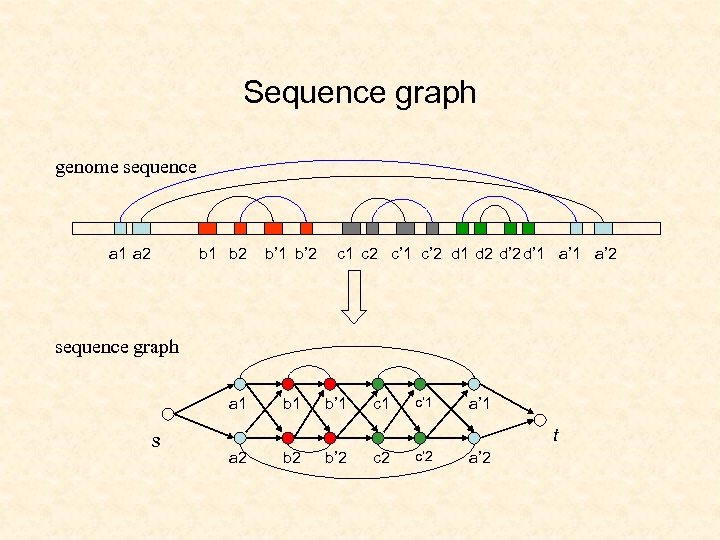Sequence graph genome sequence a 1 a 2 b 1 b 2 b’ 1 b’ 2 c 1 c 2 c’ 1 c’ 2 d 1 d 2 d’ 1 a’ 2 sequence graph a 1 s b 1 b’ 1 c’ 1 a’ 1 t a 2 b’ 2 c’ 2 a’ 2

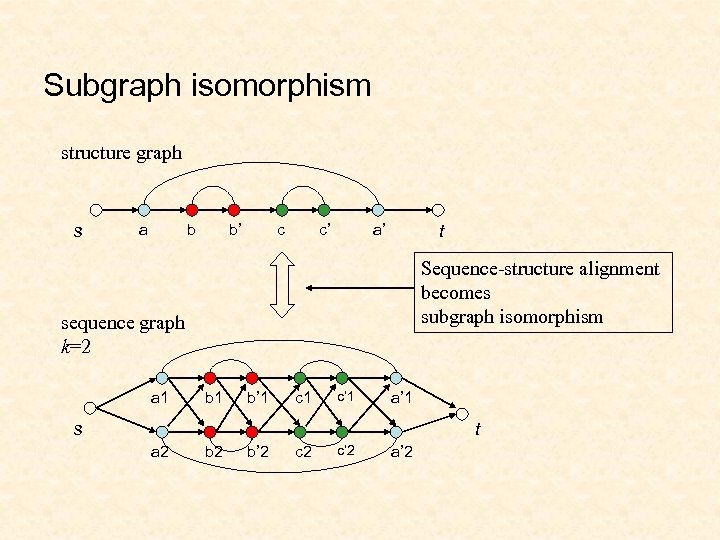Subgraph isomorphism structure graph s a b b’ c c’ a’ t Sequence-structure alignment becomes subgraph isomorphism sequence graph k=2 a 1 b’ 1 c’ 1 a’ 1 s t a 2 b’ 2 c’ 2 a’ 2

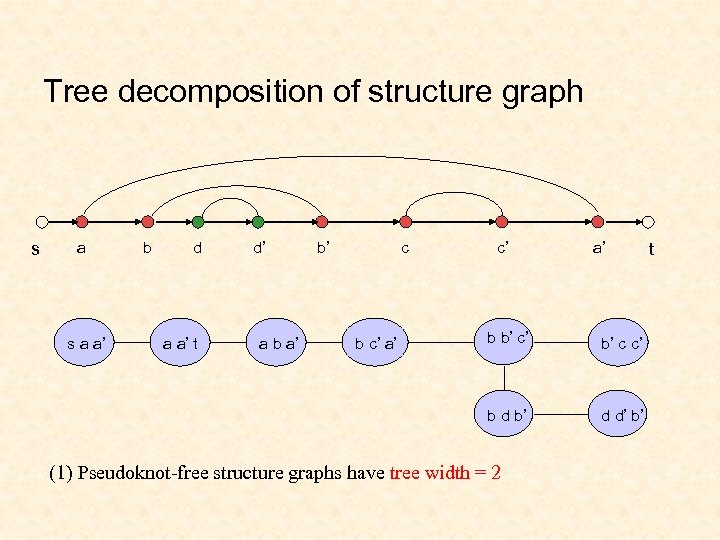Tree decomposition of structure graph s a b d d’ b’ c c’ a’ a a’ t a b a’ b c’ a’ b b’ c’ b’ c c’ b d b’ s a a’ d d’ b’ (1) Pseudoknot-free structure graphs have tree width = 2 t

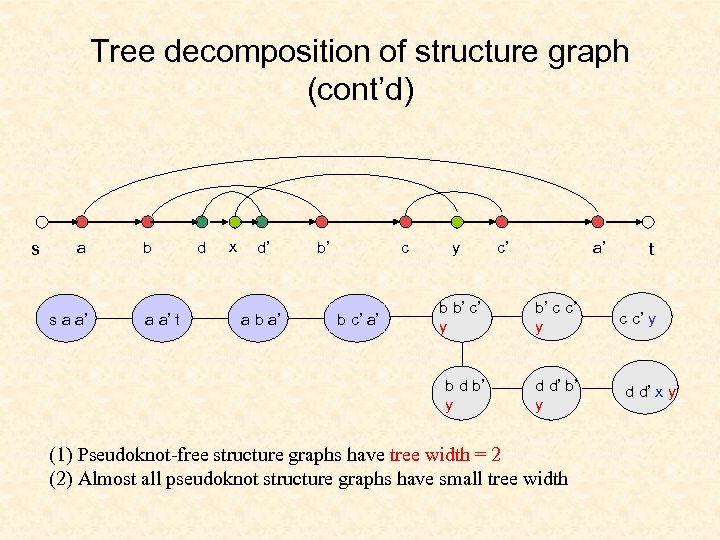Tree decomposition of structure graph (cont’d) s a b d x d’ b’ c y c’ a’ a a’ t a b a’ b c’ a’ b b’ c’ y b’ c c’ y b d b’ y s a a’ d d’ b’ y (1) Pseudoknot-free structure graphs have tree width = 2 (2) Almost all pseudoknot structure graphs have small tree width t c c’ y d d’ x y

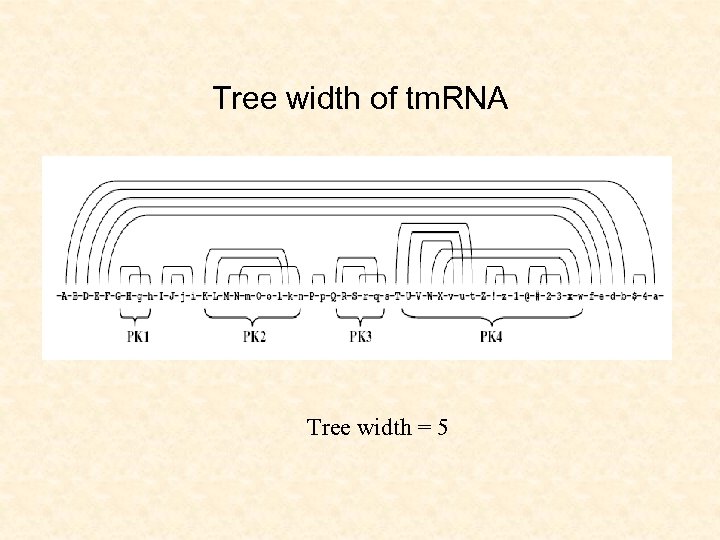Tree width of tm. RNA Tree width = 5

Tree decomposition based search algorithms (cont’s)

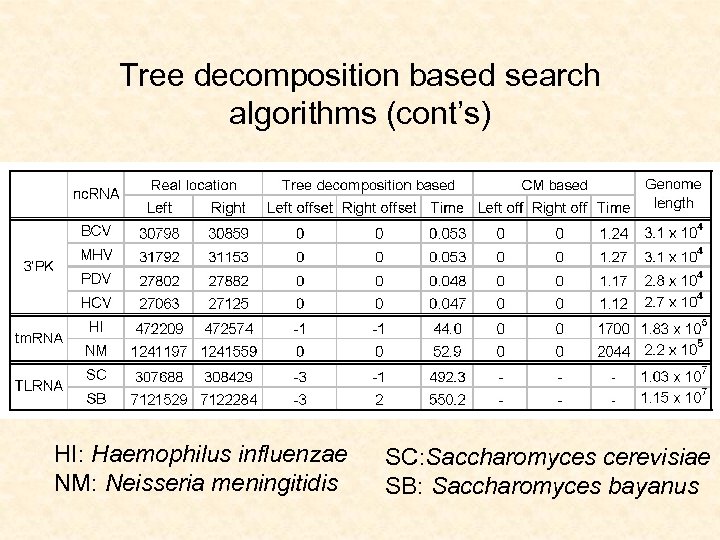Tree decomposition based search algorithms (cont’s) HI: Haemophilus influenzae NM: Neisseria meningitidis SC: Saccharomyces cerevisiae SB: Saccharomyces bayanus

RNA structure and gene search How to identify novel RNAs whose structure may deviate from the common structure of the family? - make a profile accommodate novel structures (This may mean to test more potential structures) - make the structure-sequence alignment fast enough