e7c9088771f7d582f6c32cb7a6683c38.ppt
- Количество слайдов: 56
 Computational Issues in Information Markets Lance Fortnow University of Chicago
Computational Issues in Information Markets Lance Fortnow University of Chicago
 ACM Electronic Commerce 2003 l Computation in a Distributed Information Market – l Joan Feigenbaum, Lance Fortnow, David Pennock Rahul Sami Betting Boolean Style: A Framework for Trading Securities Based on Logical Formula – Lance Fortnow, Joe Kilian, David Pennock, Michael Wellman
ACM Electronic Commerce 2003 l Computation in a Distributed Information Market – l Joan Feigenbaum, Lance Fortnow, David Pennock Rahul Sami Betting Boolean Style: A Framework for Trading Securities Based on Logical Formula – Lance Fortnow, Joe Kilian, David Pennock, Michael Wellman
 Terrorism Markets? l l l Pentagon Prepares A Futures Market On Terror Attacks - New York Times 7/29/03 Swiftly, Plan for Terrorism Futures Market Slips Into Dustbin of Idea Without a Future – NYT 7/30/03 Poindexter Will Be Quitting Over Terrorism Betting Plan – NYT 8/1/03
Terrorism Markets? l l l Pentagon Prepares A Futures Market On Terror Attacks - New York Times 7/29/03 Swiftly, Plan for Terrorism Futures Market Slips Into Dustbin of Idea Without a Future – NYT 7/30/03 Poindexter Will Be Quitting Over Terrorism Betting Plan – NYT 8/1/03
 After some thought… l l l A market in terrorism indicators was a good idea; it just got bad publicity. – Economic Scene, New York Times 7/31/03 Betting on Terror: What Markets Can Reveal – Ideas and Trends, New York Times, 8/3/03 Economics Can't Solve Everything, Can It? – Economic View, New York Times, 8/3/03
After some thought… l l l A market in terrorism indicators was a good idea; it just got bad publicity. – Economic Scene, New York Times 7/31/03 Betting on Terror: What Markets Can Reveal – Ideas and Trends, New York Times, 8/3/03 Economics Can't Solve Everything, Can It? – Economic View, New York Times, 8/3/03
 Information Markets l l Take some future potential event: The Cubs will win the pennant. Create security NL. Pennant. CHC: – – l Pays $100 if Cubs win. Pays $0 otherwise Set up a market for trading NL. Pennant. CHC. – Bids and asks. Long and short selling.
Information Markets l l Take some future potential event: The Cubs will win the pennant. Create security NL. Pennant. CHC: – – l Pays $100 if Cubs win. Pays $0 otherwise Set up a market for trading NL. Pennant. CHC. – Bids and asks. Long and short selling.
 Market Pricing l l If you believe Prob(Cubs will win)=p and are risk neutral then you would be willing to buy or sell NL. Pennant. CHC for $100 p. Price (tradesports. com, 4/3/05): 13. 0 Probability: 0. 130 Empirical studies have shown better predictive value than experts or polls.
Market Pricing l l If you believe Prob(Cubs will win)=p and are risk neutral then you would be willing to buy or sell NL. Pennant. CHC for $100 p. Price (tradesports. com, 4/3/05): 13. 0 Probability: 0. 130 Empirical studies have shown better predictive value than experts or polls.
 Questions l l Why do these markets aggregator information so well and so efficiently? How do you handle many different future nonindependent events?
Questions l l Why do these markets aggregator information so well and so efficiently? How do you handle many different future nonindependent events?
 Why do markets perform well? l l l Information markets efficiently aggregate individual information. Rational Expectations Equilibrium – Nash Equilibrium with players having different partial information will remain an equilibrium if all players have union of all information. When can rational equilibrium be achieved?
Why do markets perform well? l l l Information markets efficiently aggregate individual information. Rational Expectations Equilibrium – Nash Equilibrium with players having different partial information will remain an equilibrium if all players have union of all information. When can rational equilibrium be achieved?
 Simple Model l Let f be a Boolean function on N-variables. – l l f: {0, 1}N {0, 1} We have one security that pays off $1 if f(x) = 1 and $0 if f(x)=0. We have n players. – – Distribution x drawn from is common knowledge. Player i is given xi.
Simple Model l Let f be a Boolean function on N-variables. – l l f: {0, 1}N {0, 1} We have one security that pays off $1 if f(x) = 1 and $0 if f(x)=0. We have n players. – – Distribution x drawn from is common knowledge. Player i is given xi.
 Betting Rules l Modified Shapley-Shubik Scheme – – – Players make a bid bi of their expected value given known information. Trading price p set at average of bids bi. Player i buys (bi/p)-1 shares at price p. Price p is public but bi’s not revealed. New bids are made given updated information.
Betting Rules l Modified Shapley-Shubik Scheme – – – Players make a bid bi of their expected value given known information. Trading price p set at average of bids bi. Player i buys (bi/p)-1 shares at price p. Price p is public but bi’s not revealed. New bids are made given updated information.
 Example: OR l l l Let f(x, y) = x OR y. Initial distribution uniform. Input: x=1 and y=0. Player 1: Knows f(x, y)=1 so bids $1. Player 2: Prob(f(x, y)=1)=1/2 so bids 50¢. Price set at 75¢. After looking at bid player 2 realizes player 1 must have had 1 and will bid $1 next round.
Example: OR l l l Let f(x, y) = x OR y. Initial distribution uniform. Input: x=1 and y=0. Player 1: Knows f(x, y)=1 so bids $1. Player 2: Prob(f(x, y)=1)=1/2 so bids 50¢. Price set at 75¢. After looking at bid player 2 realizes player 1 must have had 1 and will bid $1 next round.
 Example: Parity l l l f(x, y) = x XOR y. Initial distribution uniform. Input: x=1 and y=0. Player 1: Prob(f(x, y)=1)=1/2 so bids 50¢. Player 2: Prob(f(x, y)=1)=1/2 so bids 50¢. Price set at 50¢. No trading occurs and no new information gained.
Example: Parity l l l f(x, y) = x XOR y. Initial distribution uniform. Input: x=1 and y=0. Player 1: Prob(f(x, y)=1)=1/2 so bids 50¢. Player 2: Prob(f(x, y)=1)=1/2 so bids 50¢. Price set at 50¢. No trading occurs and no new information gained.
 When do prices converge to f? l l For what functions do the prices converge to the correct value of f(x)? Theorem: The following are equivalent – – For any initial distribution, the prices for f(x) eventually converge to f(x). The function f is a weighted threshold function, i. e. , f(x) = 1 if wixi > v for fixed real wi and v.
When do prices converge to f? l l For what functions do the prices converge to the correct value of f(x)? Theorem: The following are equivalent – – For any initial distribution, the prices for f(x) eventually converge to f(x). The function f is a weighted threshold function, i. e. , f(x) = 1 if wixi > v for fixed real wi and v.
 Inputs as Hypercube Vertices 000 001 100 011 010 111
Inputs as Hypercube Vertices 000 001 100 011 010 111
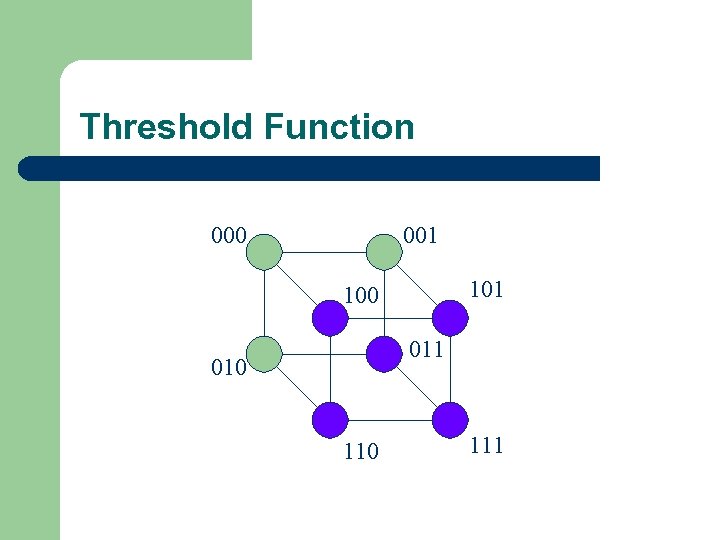 Threshold Function 000 001 100 011 010 111
Threshold Function 000 001 100 011 010 111
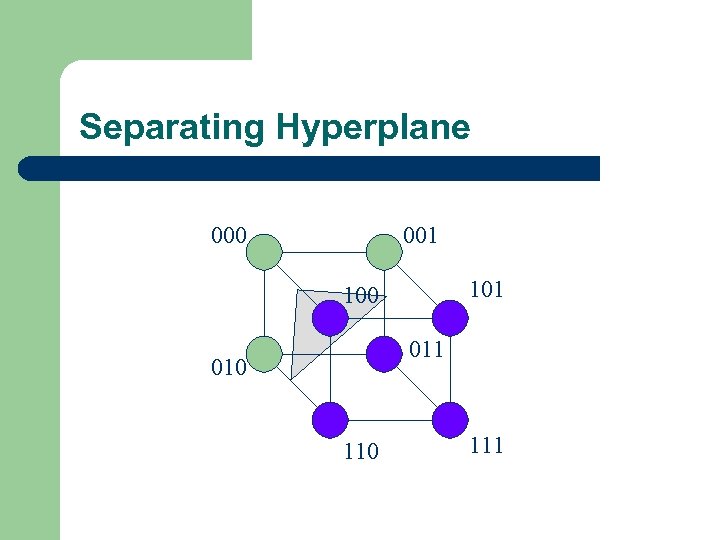 Separating Hyperplane 000 001 100 011 010 111
Separating Hyperplane 000 001 100 011 010 111
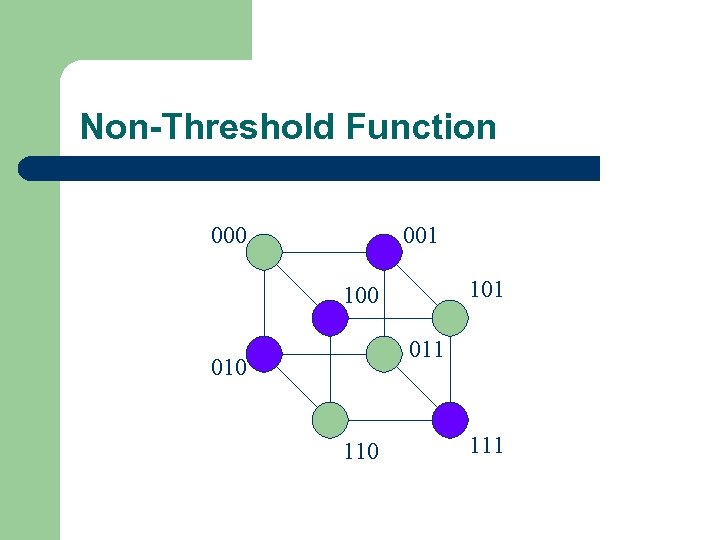 Non-Threshold Function 000 001 100 011 010 111
Non-Threshold Function 000 001 100 011 010 111
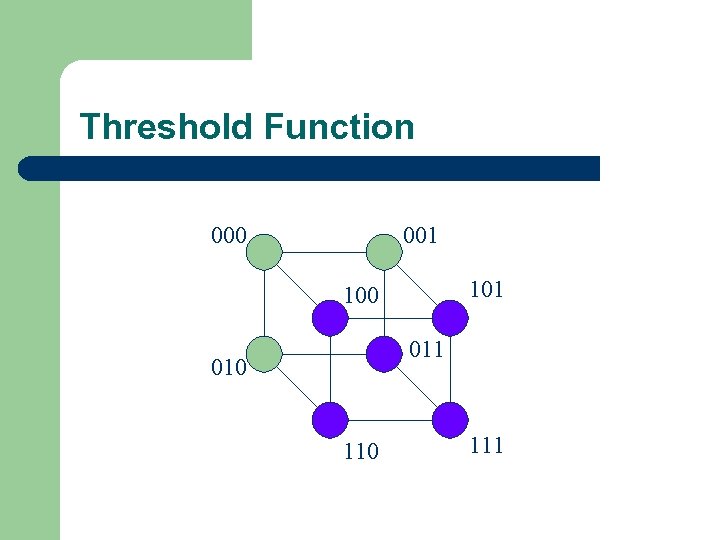 Threshold Function 000 001 100 011 010 111
Threshold Function 000 001 100 011 010 111
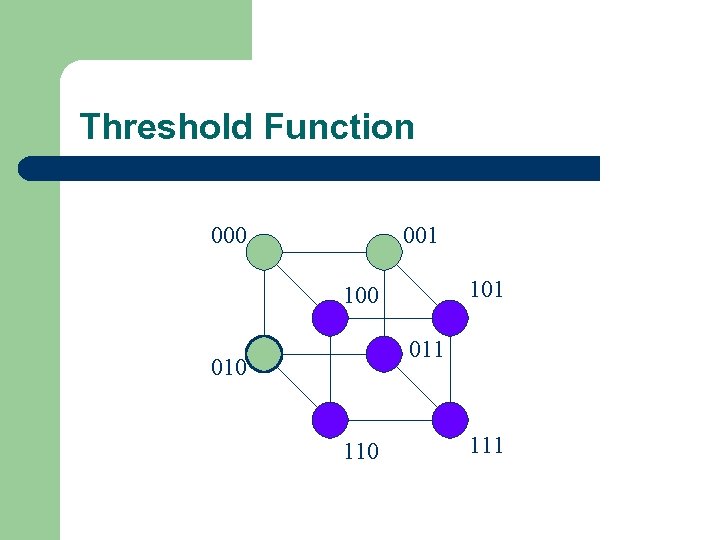 Threshold Function 000 001 100 011 010 111
Threshold Function 000 001 100 011 010 111
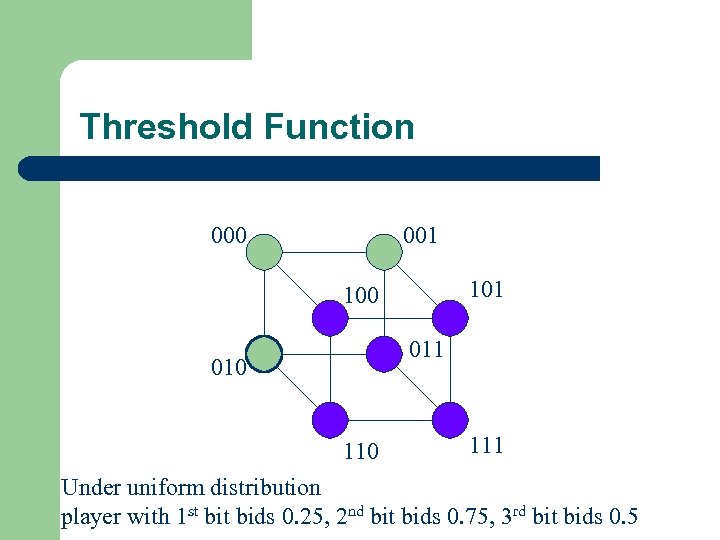 Threshold Function 000 001 100 011 010 111 Under uniform distribution player with 1 st bids 0. 25, 2 nd bit bids 0. 75, 3 rd bit bids 0. 5
Threshold Function 000 001 100 011 010 111 Under uniform distribution player with 1 st bids 0. 25, 2 nd bit bids 0. 75, 3 rd bit bids 0. 5
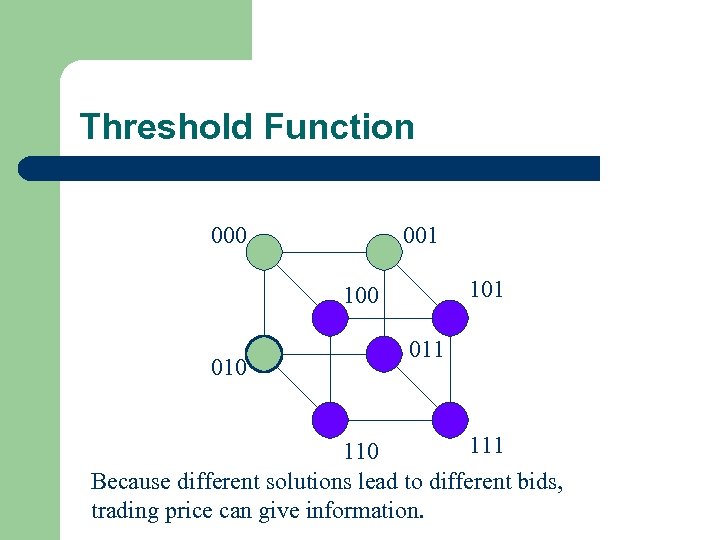 Threshold Function 000 001 100 011 110 Because different solutions lead to different bids, trading price can give information.
Threshold Function 000 001 100 011 110 Because different solutions lead to different bids, trading price can give information.
 If Trading Price Does Not Converge 000 001 100 011 110 Expected value of threshold function for zero inputs will be same for one inputs.
If Trading Price Does Not Converge 000 001 100 011 110 Expected value of threshold function for zero inputs will be same for one inputs.
 If Trading Price Does Not Converge 000 001 100 011 110 Expected value of threshold function for zero inputs will be same for one inputs. CONTRADICTION
If Trading Price Does Not Converge 000 001 100 011 110 Expected value of threshold function for zero inputs will be same for one inputs. CONTRADICTION
 Non-Threshold Function 000 001 100 011 010 111
Non-Threshold Function 000 001 100 011 010 111
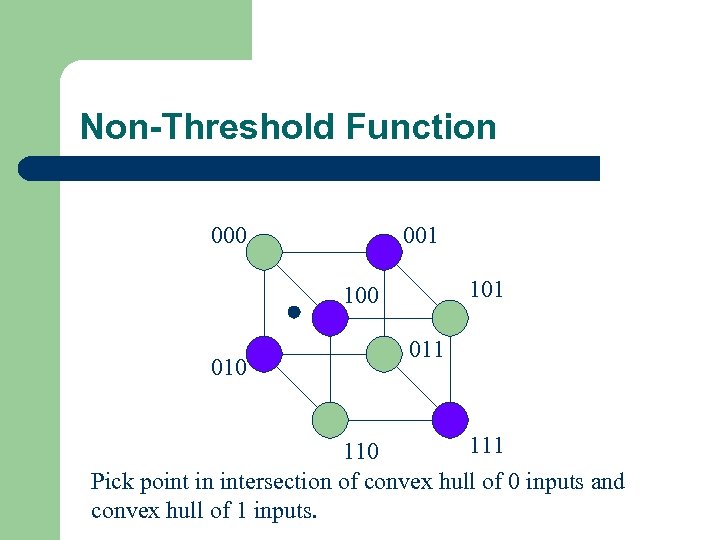 Non-Threshold Function 000 001 100 011 110 Pick point in intersection of convex hull of 0 inputs and convex hull of 1 inputs.
Non-Threshold Function 000 001 100 011 110 Pick point in intersection of convex hull of 0 inputs and convex hull of 1 inputs.
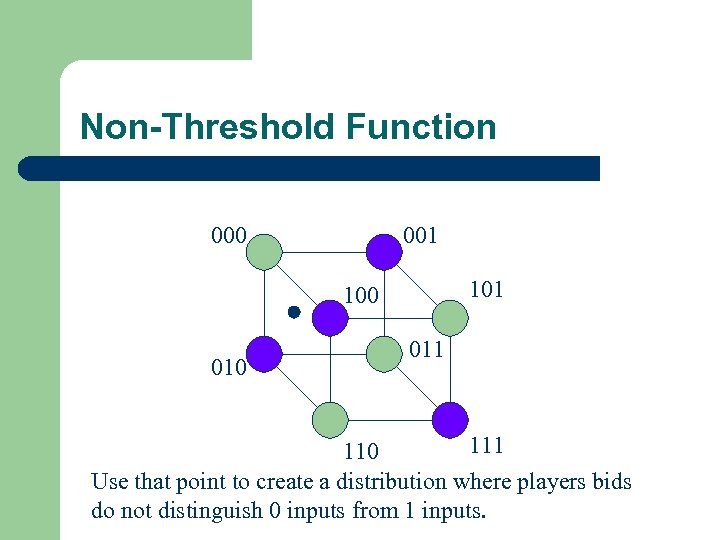 Non-Threshold Function 000 001 100 011 110 Use that point to create a distribution where players bids do not distinguish 0 inputs from 1 inputs.
Non-Threshold Function 000 001 100 011 110 Use that point to create a distribution where players bids do not distinguish 0 inputs from 1 inputs.
 Efficiency Concerns l l l In most natural cases, these markets converge to correct answer very quickly. We show that if market converges, it converges in at most n rounds. We give an example where market requires n/2 rounds to converge.
Efficiency Concerns l l l In most natural cases, these markets converge to correct answer very quickly. We show that if market converges, it converges in at most n rounds. We give an example where market requires n/2 rounds to converge.
 Other Directions l Specific Distributions – l Dani – Modk function for k>2 converges over the uniform distribution. Future Research Questions – – Show quick updates to small change of information. Can one use a circuit of threshold functions (neural net) to make markets more efficient?
Other Directions l Specific Distributions – l Dani – Modk function for k>2 converges over the uniform distribution. Future Research Questions – – Show quick updates to small change of information. Can one use a circuit of threshold functions (neural net) to make markets more efficient?
 Experimental Results l l l Experiments performed at Penn State by Yiling Chen and Tony Kwasnica Using five agents (inputs) each gets A/B signal Uniform Distribution Majority (at least three A) Parity (odd)
Experimental Results l l l Experiments performed at Penn State by Yiling Chen and Tony Kwasnica Using five agents (inputs) each gets A/B signal Uniform Distribution Majority (at least three A) Parity (odd)
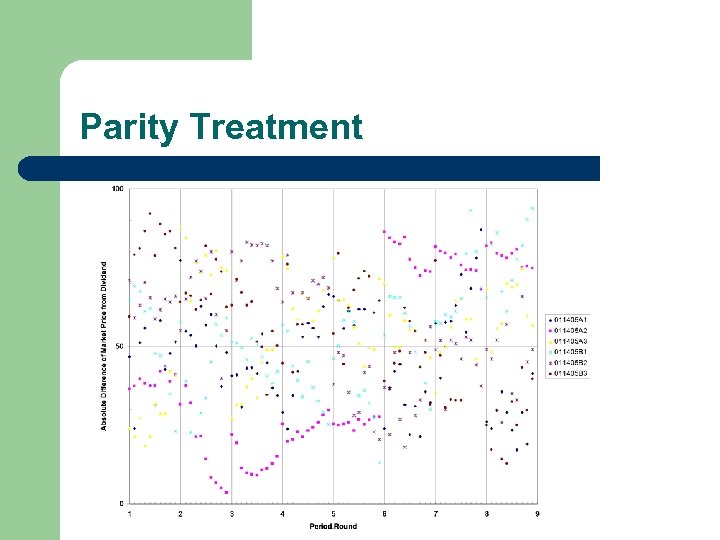 Parity Treatment
Parity Treatment
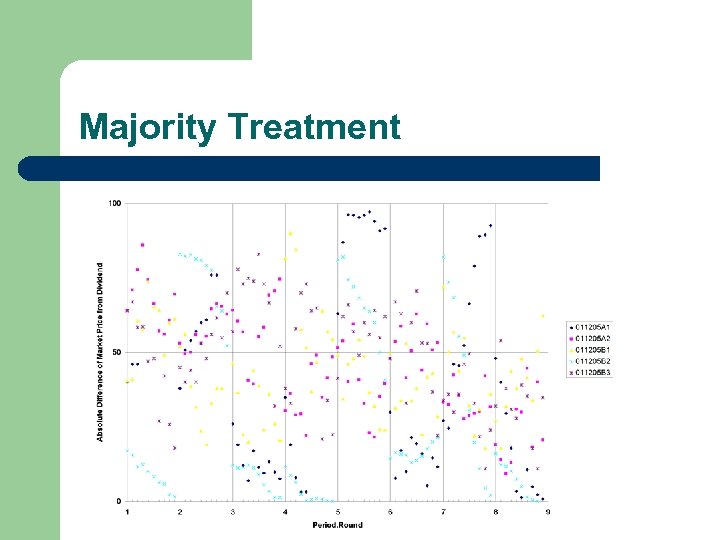 Majority Treatment
Majority Treatment
 How do we handle many securities? l What if we have lots of securities that reflect different states of the future, yet have some dependence among them?
How do we handle many securities? l What if we have lots of securities that reflect different states of the future, yet have some dependence among them?
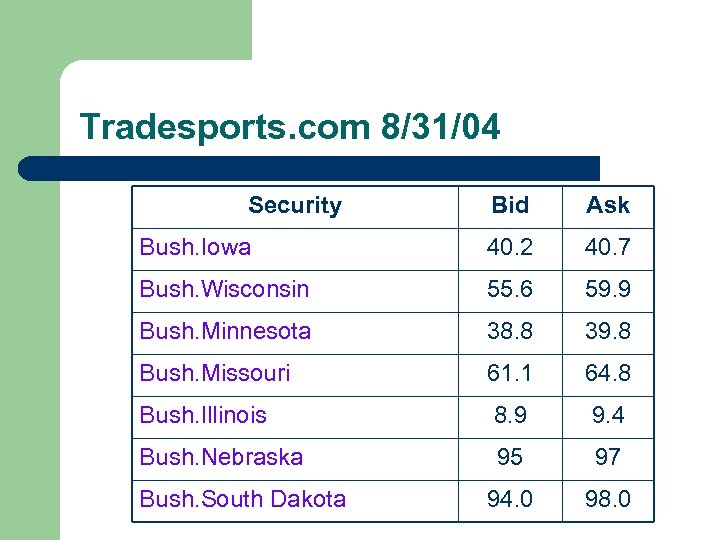 Tradesports. com 8/31/04 Security Bid Ask Bush. Iowa 40. 2 40. 7 Bush. Wisconsin 55. 6 59. 9 Bush. Minnesota 38. 8 39. 8 Bush. Missouri 61. 1 64. 8 Bush. Illinois 8. 9 9. 4 Bush. Nebraska 95 97 94. 0 98. 0 Bush. South Dakota
Tradesports. com 8/31/04 Security Bid Ask Bush. Iowa 40. 2 40. 7 Bush. Wisconsin 55. 6 59. 9 Bush. Minnesota 38. 8 39. 8 Bush. Missouri 61. 1 64. 8 Bush. Illinois 8. 9 9. 4 Bush. Nebraska 95 97 94. 0 98. 0 Bush. South Dakota
 Compound Securities (IL and NJ) or (not IL and not NJ) l l This security pays off $100 if Bush wins or loses both Illinois and New Jersey. Not derivable as a linear combination of base securities.
Compound Securities (IL and NJ) or (not IL and not NJ) l l This security pays off $100 if Bush wins or loses both Illinois and New Jersey. Not derivable as a linear combination of base securities.
 Example from Tradesports l l Ohio: Bid 63. 4 Ask 66. 9 Florida: Bid 57. 5 Ask 59. 5 OH AND FL: Bid 55. 0 Ask 56. 8 FL AND (NOT OH) = FL – (FL AND OH) – Buy FL at 59. 5 – Sell OH AND FL for 55. 0 – Cost of FL AND (NOT OH) is 4. 5
Example from Tradesports l l Ohio: Bid 63. 4 Ask 66. 9 Florida: Bid 57. 5 Ask 59. 5 OH AND FL: Bid 55. 0 Ask 56. 8 FL AND (NOT OH) = FL – (FL AND OH) – Buy FL at 59. 5 – Sell OH AND FL for 55. 0 – Cost of FL AND (NOT OH) is 4. 5
 Large Number of Securities 250 l 2 l l possible functions over the fifty base securities corresponding to the states. “Only” 250 securities needed to span the space of all possible functions. Won’t be enough liquidity for nearly all possible securities.
Large Number of Securities 250 l 2 l l possible functions over the fifty base securities corresponding to the states. “Only” 250 securities needed to span the space of all possible functions. Won’t be enough liquidity for nearly all possible securities.
 Trading different securities l l Bid of $40 for (ME and not IN) Ask of $30 for (not IN) Market maker can sell (ME and not IN) and buy (not IN), pocketing $10 If Bush wins Maine and loses Indiana – – Both securities payoff Maker nets $10
Trading different securities l l Bid of $40 for (ME and not IN) Ask of $30 for (not IN) Market maker can sell (ME and not IN) and buy (not IN), pocketing $10 If Bush wins Maine and loses Indiana – – Both securities payoff Maker nets $10
 Trading different securities l l Bid of $40 for (ME and not IN) Ask of $30 for (not IN) Market maker can sell (ME and not IN) and buy (not IN), pocketing $10 If Bush wins Indiana – – Both Securities do not payoff Maker nets $10
Trading different securities l l Bid of $40 for (ME and not IN) Ask of $30 for (not IN) Market maker can sell (ME and not IN) and buy (not IN), pocketing $10 If Bush wins Indiana – – Both Securities do not payoff Maker nets $10
 Trading different securities l l Bid of $40 for (ME and not IN) Ask of $30 for (not IN) Market maker can sell (ME and not IN) and buy (not IN), pocketing $10 If Bush loses both Indiana and Maine – – – (ME and not IN) does not require payment Maker receives $100 for (not IN) Maker makes $110
Trading different securities l l Bid of $40 for (ME and not IN) Ask of $30 for (not IN) Market maker can sell (ME and not IN) and buy (not IN), pocketing $10 If Bush loses both Indiana and Maine – – – (ME and not IN) does not require payment Maker receives $100 for (not IN) Maker makes $110
 Slightly More Complicated Example l l Ask of $40 for TX Bid of $10 for (TX and not FL) Bid of $20 for (TX and FL) Maker can sell TX and buy (TX and not FL) and (TX and FL). – – Maker pockets $10. In every case payoffs will cancel out.
Slightly More Complicated Example l l Ask of $40 for TX Bid of $10 for (TX and not FL) Bid of $20 for (TX and FL) Maker can sell TX and buy (TX and not FL) and (TX and FL). – – Maker pockets $10. In every case payoffs will cancel out.
 Complexity of Matching l l What is the computational complexity of finding a matching in a set of buy and ask orders? The answer depends on two factors – – The number of base securities. Whether we allow orders to be partially filled.
Complexity of Matching l l What is the computational complexity of finding a matching in a set of buy and ask orders? The answer depends on two factors – – The number of base securities. Whether we allow orders to be partially filled.
 Indivisible Orders l l l Ask of HI at $30 Ask of CT at $30 Ask of (HI xor CT) at $30 Bid of (HI or CT) at $50 A match is impossible if can only buy or sell zero or one unit of each security.
Indivisible Orders l l l Ask of HI at $30 Ask of CT at $30 Ask of (HI xor CT) at $30 Bid of (HI or CT) at $50 A match is impossible if can only buy or sell zero or one unit of each security.
 Divisible Orders l l Ask of HI at $30 Ask of CT at $30 Ask of (HI xor CT) at $30 Bid of (HI or CT) at $50
Divisible Orders l l Ask of HI at $30 Ask of CT at $30 Ask of (HI xor CT) at $30 Bid of (HI or CT) at $50
 Divisible Orders l l Ask of HI at $30 Ask of CT at $30 Ask of (HI xor CT) at $30 Bid of (HI or CT) at $50 Maker buys ½ Maker sells 1
Divisible Orders l l Ask of HI at $30 Ask of CT at $30 Ask of (HI xor CT) at $30 Bid of (HI or CT) at $50 Maker buys ½ Maker sells 1
 Divisible Orders l l l l Ask of HI at $30 Maker buys ½ Ask of CT at $30 Maker buys ½ Ask of (HI xor CT) at $30 Maker buys ½ Bid of (HI or CT) at $50 Maker sells 1 Maker pays 3 x($30/2)=$45 and receives $50. Maker clears $5. Securities payoffs cancel.
Divisible Orders l l l l Ask of HI at $30 Maker buys ½ Ask of CT at $30 Maker buys ½ Ask of (HI xor CT) at $30 Maker buys ½ Bid of (HI or CT) at $50 Maker sells 1 Maker pays 3 x($30/2)=$45 and receives $50. Maker clears $5. Securities payoffs cancel.
 Divisible Orders l l l l Ask of HI at $30 Maker buys ½ Ask of CT at $30 Maker buys ½ Ask of (HI xor CT) at $30 Maker buys ½ Bid of (HI or CT) at $50 Maker sells 1 Suppose Bush wins Hawaii and Connecticut Owes $100 for full share of (HI or CT) Receives $50 for each ½ share of HI and CT
Divisible Orders l l l l Ask of HI at $30 Maker buys ½ Ask of CT at $30 Maker buys ½ Ask of (HI xor CT) at $30 Maker buys ½ Bid of (HI or CT) at $50 Maker sells 1 Suppose Bush wins Hawaii and Connecticut Owes $100 for full share of (HI or CT) Receives $50 for each ½ share of HI and CT
 Complexity of Finding a Match l l Suppose we have n securities. Large number of base securities (about n) Small number of base securities (about log n) Are securities allowed to be divisible?
Complexity of Finding a Match l l Suppose we have n securities. Large number of base securities (about n) Small number of base securities (about log n) Are securities allowed to be divisible?
 Complexity of Matching Problem Small Number of Base Securities Divisible Indivisible Large Number of Base Securities Polynomial-Time Computable co-NP-complete 2 -complete
Complexity of Matching Problem Small Number of Base Securities Divisible Indivisible Large Number of Base Securities Polynomial-Time Computable co-NP-complete 2 -complete
 Complexity of Matching Problem Small Number of Base Securities Divisible Indivisible Large Number of Base Securities Linear Programming Polynomial-Time co-NP-complete Computable NP-complete 2 -complete
Complexity of Matching Problem Small Number of Base Securities Divisible Indivisible Large Number of Base Securities Linear Programming Polynomial-Time co-NP-complete Computable NP-complete 2 -complete
 Complexity of Matching Problem Small Number of Base Securities Divisible Indivisible Polynomial-Time Computable NP-complete Large Number of Base Securities Reduction from SAT co-NP-complete 2 -complete
Complexity of Matching Problem Small Number of Base Securities Divisible Indivisible Polynomial-Time Computable NP-complete Large Number of Base Securities Reduction from SAT co-NP-complete 2 -complete
 Complexity of Matching Problem Small Number of Base Securities Divisible Indivisible Large Number of Base Securities Polynomial-Time Computable Co-NP-complete Reduction from X 3 C NP-complete 2 -complete
Complexity of Matching Problem Small Number of Base Securities Divisible Indivisible Large Number of Base Securities Polynomial-Time Computable Co-NP-complete Reduction from X 3 C NP-complete 2 -complete
 Complexity of Matching Problem Small Number of Base Securities Divisible Indivisible Large Number of Base Securities Polynomial-Time Computable co-NP-complete 2 -complete Reduction from True -Formulas
Complexity of Matching Problem Small Number of Base Securities Divisible Indivisible Large Number of Base Securities Polynomial-Time Computable co-NP-complete 2 -complete Reduction from True -Formulas
 Complexity of Matching Problem Small Number of Base Securities Divisible Indivisible Large Number of Base Securities Polynomial-Time Computable co-NP-complete 2 -complete Remains complete even if securities are of form (WI and not TN)
Complexity of Matching Problem Small Number of Base Securities Divisible Indivisible Large Number of Base Securities Polynomial-Time Computable co-NP-complete 2 -complete Remains complete even if securities are of form (WI and not TN)
 Extensions l l l Conditional Securities Bush. 2004|DEM. 2004. VP. Edwards Far more complicated payoffs and securities described by circuits instead of formula. Same complexity bounds hold for these extensions.
Extensions l l l Conditional Securities Bush. 2004|DEM. 2004. VP. Edwards Far more complicated payoffs and securities described by circuits instead of formula. Same complexity bounds hold for these extensions.
 Future Directions l Other matching rules – – l l How to distribute surplus made by maker? Trader Optimization Issues – – l Maximize utility subject to no risk Maximize expected utility perhaps with risk How to choose securities, prices Complexity of bids Approximation and Heuristic Algorithms
Future Directions l Other matching rules – – l l How to distribute surplus made by maker? Trader Optimization Issues – – l Maximize utility subject to no risk Maximize expected utility perhaps with risk How to choose securities, prices Complexity of bids Approximation and Heuristic Algorithms
 A “Physics” Approach to Research l l l Our models overly simplify the real world. Any model that takes into account all of the factors of a financial market will be too hard to properly analyze. Approach: – – – Make unrealistic assumptions of the world. Test results in experimental economics labs. Repeat.
A “Physics” Approach to Research l l l Our models overly simplify the real world. Any model that takes into account all of the factors of a financial market will be too hard to properly analyze. Approach: – – – Make unrealistic assumptions of the world. Test results in experimental economics labs. Repeat.


