d647b8c7f60c9e15637a5c82578036ab.ppt
- Количество слайдов: 88
 Computational Geometry and Spatial Data Mining Marc van Kreveld Department of Information and Computing Sciences Utrecht University
Computational Geometry and Spatial Data Mining Marc van Kreveld Department of Information and Computing Sciences Utrecht University
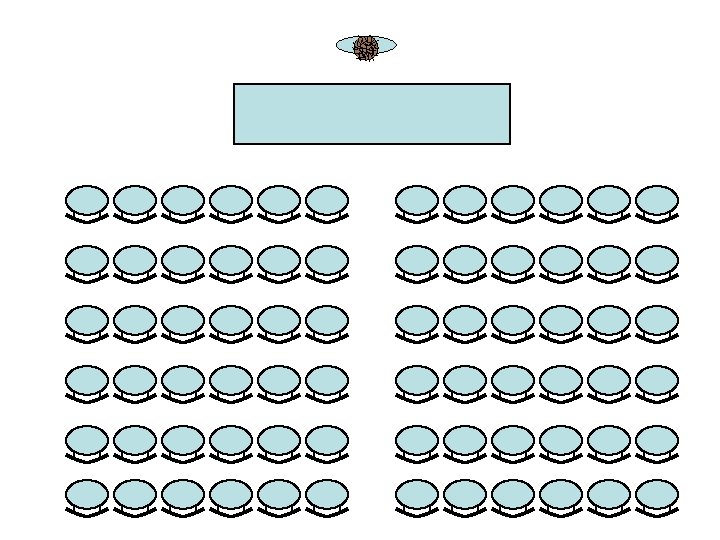
 Clustering? • Are the people clustered in this room? How do we define a cluster? • In spatial data mining we have objects/ entities with a location given by coordinates • Cluster definitions involve distance between locations
Clustering? • Are the people clustered in this room? How do we define a cluster? • In spatial data mining we have objects/ entities with a location given by coordinates • Cluster definitions involve distance between locations
 Clustering - options • • Determine whether clustering occurs Determine the degree of clustering Determine the clusters Determine the largest cluster • Determine the outliers
Clustering - options • • Determine whether clustering occurs Determine the degree of clustering Determine the clusters Determine the largest cluster • Determine the outliers
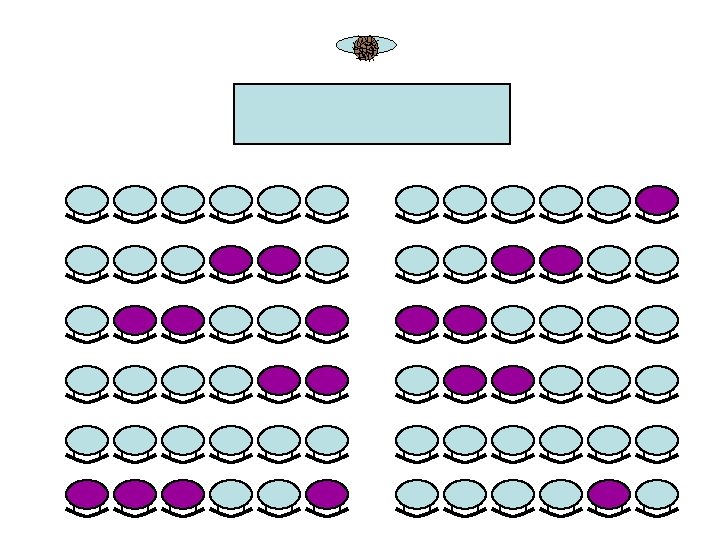
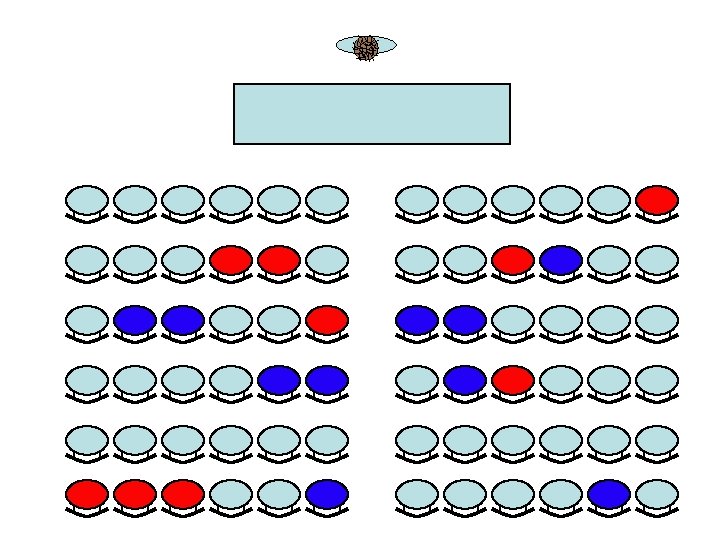
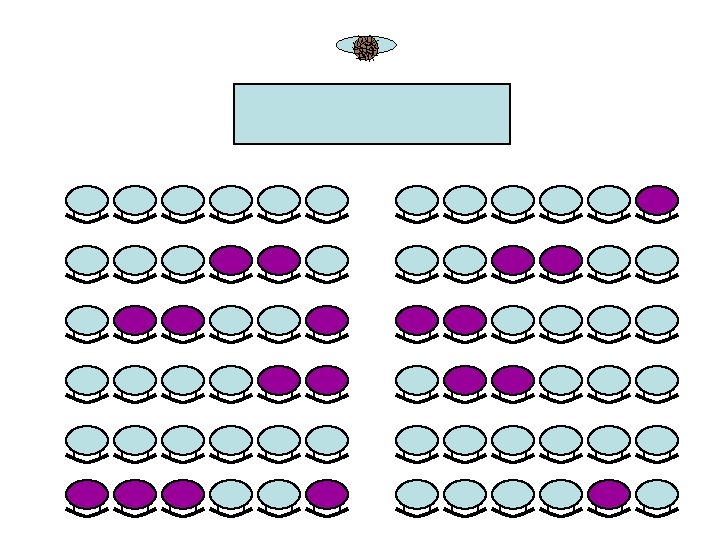
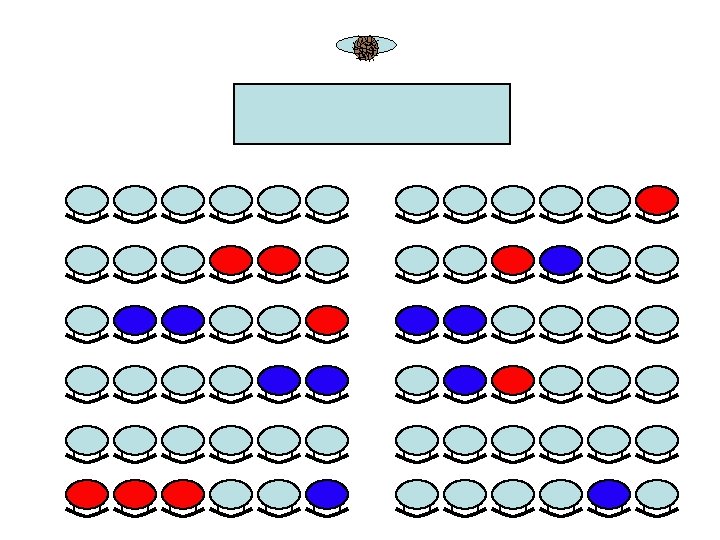
 Co-location • Are the men clustered? • Are the women clustered? • Is there a co-location of men and women?
Co-location • Are the men clustered? • Are the women clustered? • Is there a co-location of men and women?
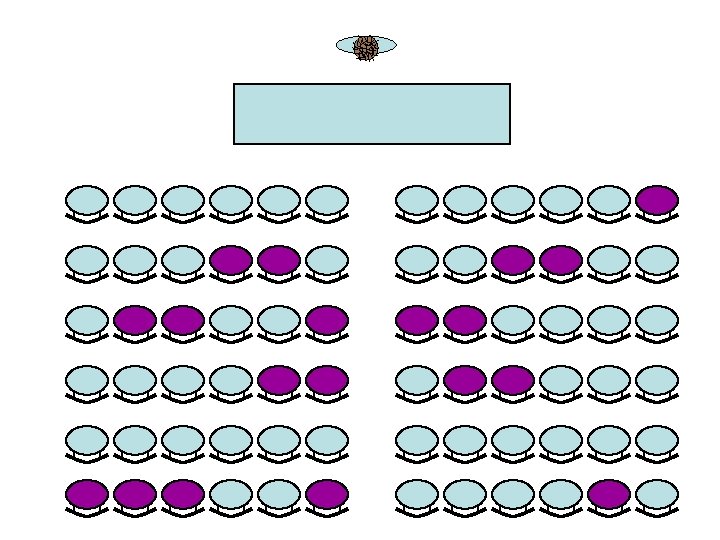
 Co-location • Like before, we may be interested in – is there co-location? – the degree of co-location – the largest co-location – the co-locations themselves – the objects not involved in co-location
Co-location • Like before, we may be interested in – is there co-location? – the degree of co-location – the largest co-location – the co-locations themselves – the objects not involved in co-location
 Spatio-temporal data • Locations have a time stamp • Interesting patterns involve space and time
Spatio-temporal data • Locations have a time stamp • Interesting patterns involve space and time
 Trajectory data • Entities with a trajectory (time-stamped motion path) • Interesting patterns involve subgroups with similar heading, expected arrival, joint motion, . . . • n entities = trajectories; n = 10 – 100, 000 • t time steps; t = 10 – 100, 000 input size is nt • m size subgroup (unknown); m = 10 – 100, 000
Trajectory data • Entities with a trajectory (time-stamped motion path) • Interesting patterns involve subgroups with similar heading, expected arrival, joint motion, . . . • n entities = trajectories; n = 10 – 100, 000 • t time steps; t = 10 – 100, 000 input size is nt • m size subgroup (unknown); m = 10 – 100, 000
 Examples of trajectory data • • • Tracked animals (buffalo, birds, . . . ) Tracked people (potential terrorists) Tracked GSMs (e. g. for traffic purposes) Trajectories of tornadoes Sports scene analysis (players on a soccer field)
Examples of trajectory data • • • Tracked animals (buffalo, birds, . . . ) Tracked people (potential terrorists) Tracked GSMs (e. g. for traffic purposes) Trajectories of tornadoes Sports scene analysis (players on a soccer field)
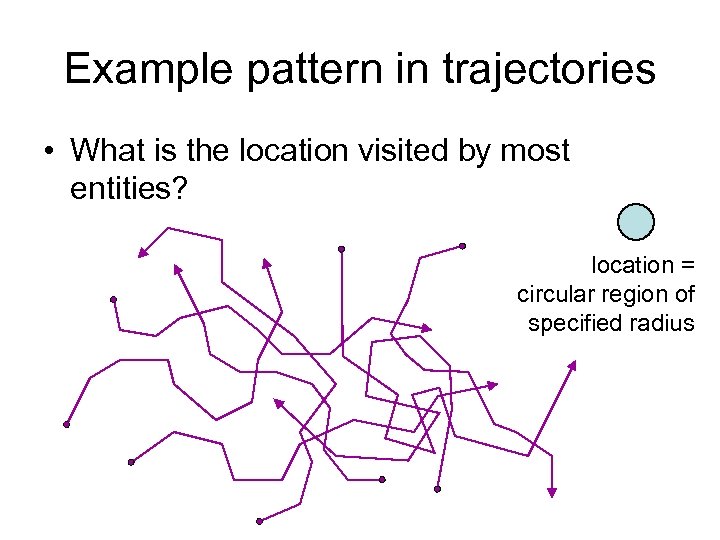 Example pattern in trajectories • What is the location visited by most entities? location = circular region of specified radius
Example pattern in trajectories • What is the location visited by most entities? location = circular region of specified radius
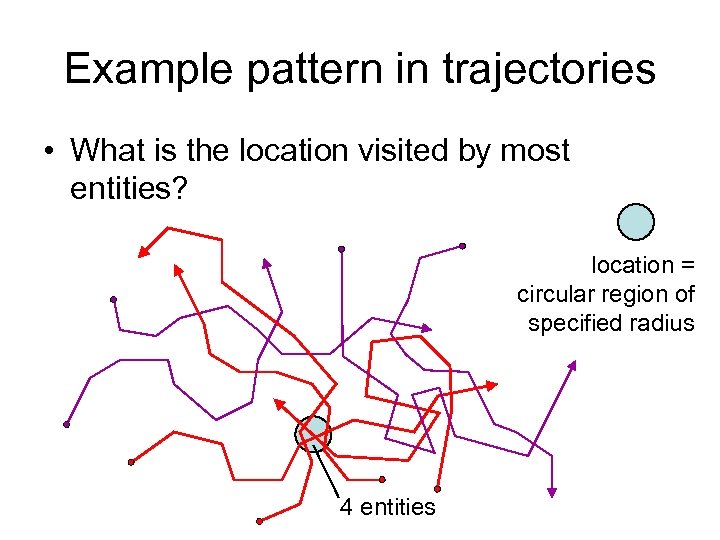 Example pattern in trajectories • What is the location visited by most entities? location = circular region of specified radius 4 entities
Example pattern in trajectories • What is the location visited by most entities? location = circular region of specified radius 4 entities
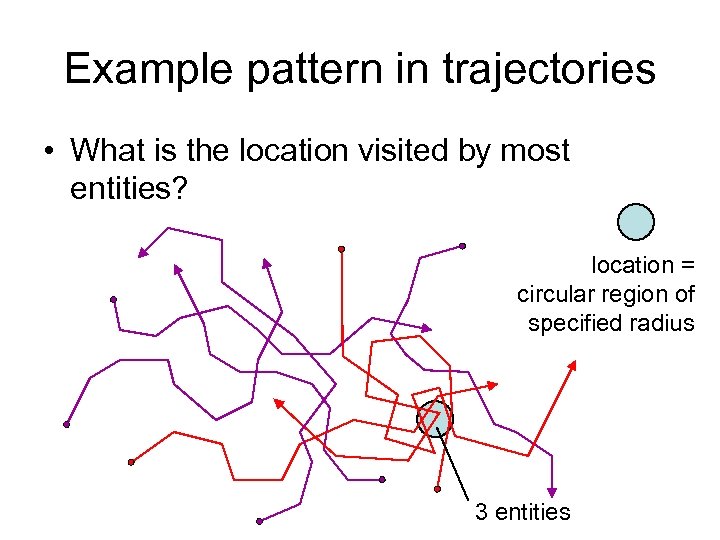 Example pattern in trajectories • What is the location visited by most entities? location = circular region of specified radius 3 entities
Example pattern in trajectories • What is the location visited by most entities? location = circular region of specified radius 3 entities
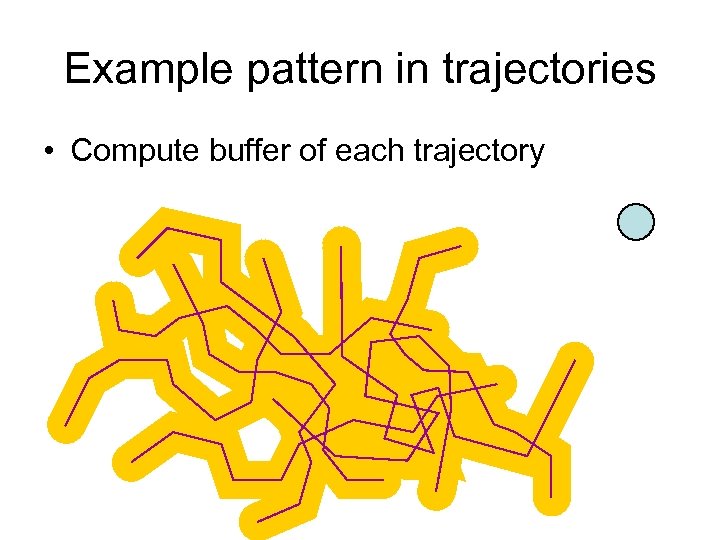 Example pattern in trajectories • Compute buffer of each trajectory
Example pattern in trajectories • Compute buffer of each trajectory
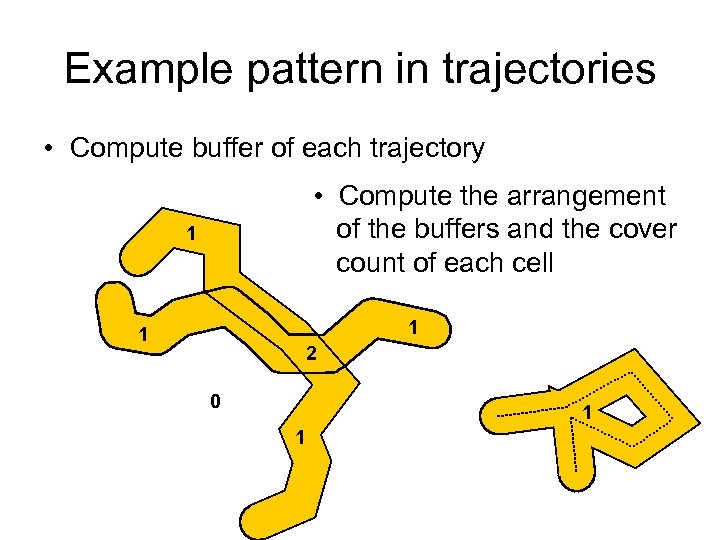 Example pattern in trajectories • Compute buffer of each trajectory • Compute the arrangement of the buffers and the cover count of each cell 1 1 1 2 0 1 1
Example pattern in trajectories • Compute buffer of each trajectory • Compute the arrangement of the buffers and the cover count of each cell 1 1 1 2 0 1 1
 Example pattern in trajectories • One trajectory has t time stamps; its buffer can be computed in O(t log t) time • All buffers can be computed in O(nt log t) time • The arrangement can be computed in O(nt log (nt) + k) time, where k = O( (nt)2 ) is the complexity of the arrangement • Cell cover counts are determined in O(k) time
Example pattern in trajectories • One trajectory has t time stamps; its buffer can be computed in O(t log t) time • All buffers can be computed in O(nt log t) time • The arrangement can be computed in O(nt log (nt) + k) time, where k = O( (nt)2 ) is the complexity of the arrangement • Cell cover counts are determined in O(k) time
 Example pattern in trajectories • Total: O(nt log (nt) + k) time • If the most visited location is visited by m entities, this is O(nt log (nt) + ntm) • Note: input size is nt ; n entities, each with location at t moments
Example pattern in trajectories • Total: O(nt log (nt) + k) time • If the most visited location is visited by m entities, this is O(nt log (nt) + ntm) • Note: input size is nt ; n entities, each with location at t moments
 Patterns in entity data Spatial data Spatio-temporal data • n points (locations) • Distance is important • n trajectories, each has t time steps • Distance is timedependent – clustering pattern • Presence of attributes (e. g. man/woman): – co-location patterns – flock pattern – meet pattern • Heading and speed are important and are also time-dependent
Patterns in entity data Spatial data Spatio-temporal data • n points (locations) • Distance is important • n trajectories, each has t time steps • Distance is timedependent – clustering pattern • Presence of attributes (e. g. man/woman): – co-location patterns – flock pattern – meet pattern • Heading and speed are important and are also time-dependent
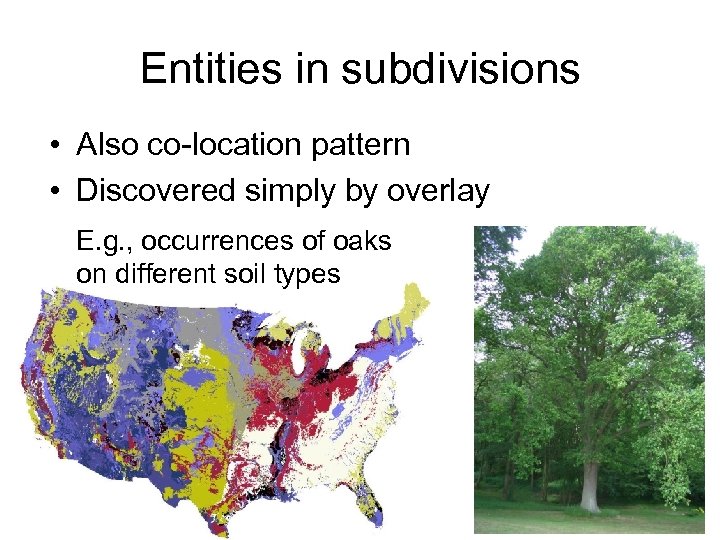 Entities in subdivisions • Also co-location pattern • Discovered simply by overlay E. g. , occurrences of oaks on different soil types
Entities in subdivisions • Also co-location pattern • Discovered simply by overlay E. g. , occurrences of oaks on different soil types
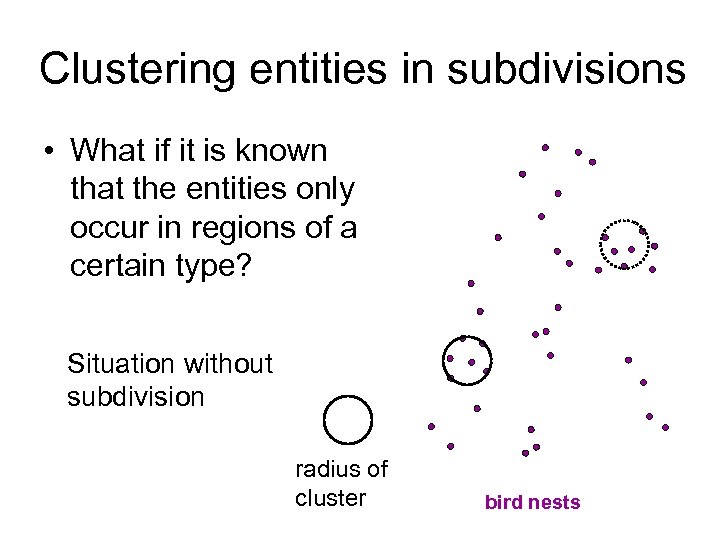 Clustering entities in subdivisions • What if it is known that the entities only occur in regions of a certain type? Situation without subdivision radius of cluster bird nests
Clustering entities in subdivisions • What if it is known that the entities only occur in regions of a certain type? Situation without subdivision radius of cluster bird nests
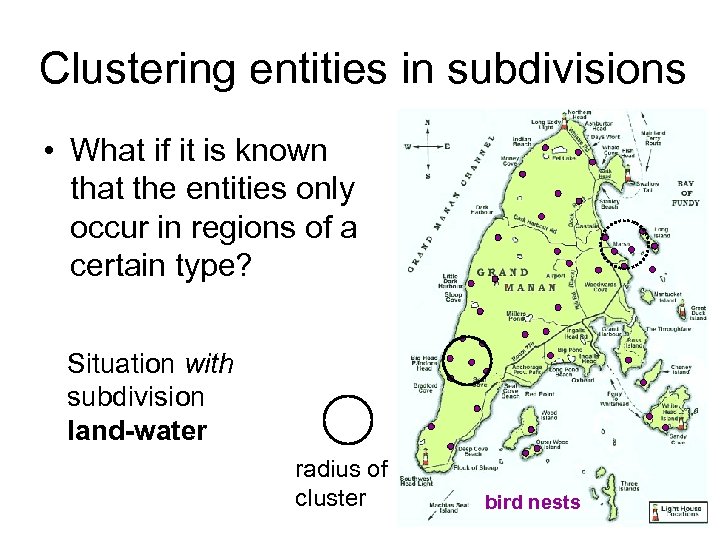 Clustering entities in subdivisions • What if it is known that the entities only occur in regions of a certain type? Situation with subdivision land-water radius of cluster bird nests
Clustering entities in subdivisions • What if it is known that the entities only occur in regions of a certain type? Situation with subdivision land-water radius of cluster bird nests
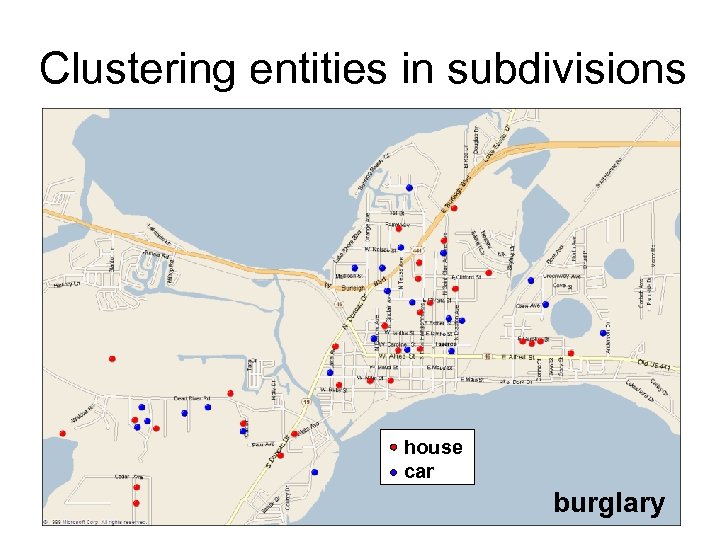 Clustering entities in subdivisions house car burglary
Clustering entities in subdivisions house car burglary
 Region-restricted clustering Joint research with Joachim Gudmundsson (NICTA, Sydney) and Giri Narasimhan (U of F, Miami), 2006 • Determine clusters in point sets that are sensitive to the geographic context (at least, for the relevant aspects) Assume that a set of regions is given where points can only be, how should we define clusters?
Region-restricted clustering Joint research with Joachim Gudmundsson (NICTA, Sydney) and Giri Narasimhan (U of F, Miami), 2006 • Determine clusters in point sets that are sensitive to the geographic context (at least, for the relevant aspects) Assume that a set of regions is given where points can only be, how should we define clusters?
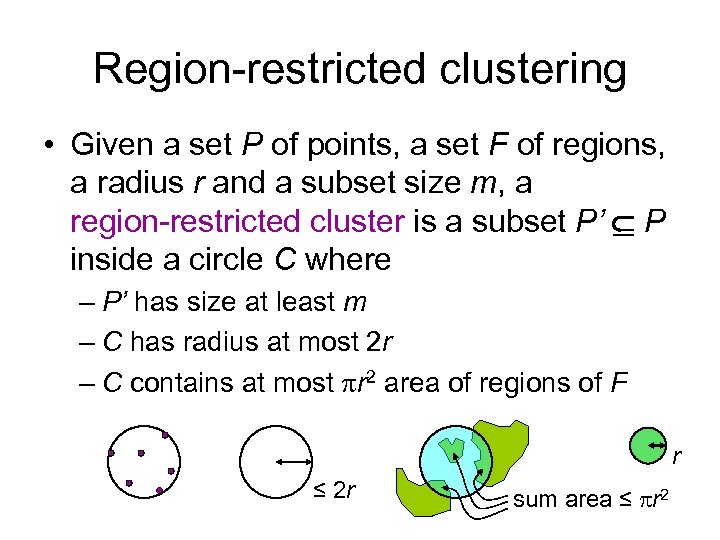 Region-restricted clustering • Given a set P of points, a set F of regions, a radius r and a subset size m, a region-restricted cluster is a subset P’ P inside a circle C where – P’ has size at least m – C has radius at most 2 r – C contains at most r 2 area of regions of F r ≤ 2 r sum area ≤ r 2
Region-restricted clustering • Given a set P of points, a set F of regions, a radius r and a subset size m, a region-restricted cluster is a subset P’ P inside a circle C where – P’ has size at least m – C has radius at most 2 r – C contains at most r 2 area of regions of F r ≤ 2 r sum area ≤ r 2
 Region-restricted clustering • Given a set P of n points, a set F of polygons with nf edges in total, and values for r and m, report all region-restricted clusters of exactly m points • Exactly m points? • “Real” clustering (partition)? • Outliers?
Region-restricted clustering • Given a set P of n points, a set F of polygons with nf edges in total, and values for r and m, report all region-restricted clusters of exactly m points • Exactly m points? • “Real” clustering (partition)? • Outliers?
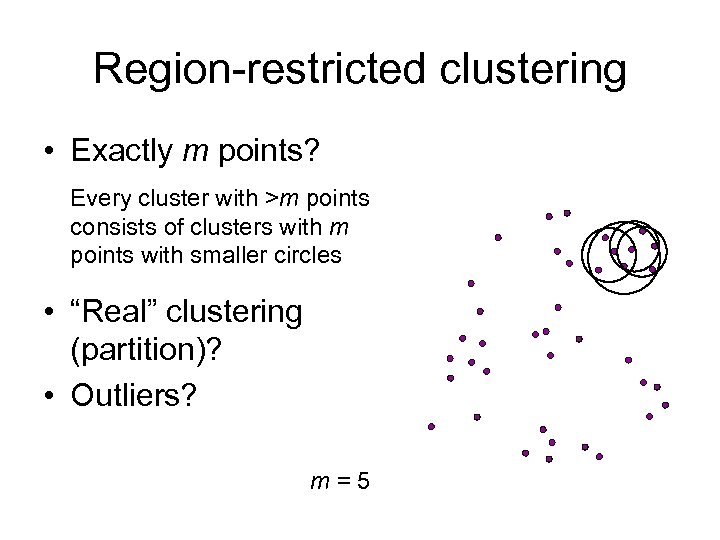 Region-restricted clustering • Exactly m points? Every cluster with >m points consists of clusters with m points with smaller circles • “Real” clustering (partition)? • Outliers? m=5
Region-restricted clustering • Exactly m points? Every cluster with >m points consists of clusters with m points with smaller circles • “Real” clustering (partition)? • Outliers? m=5
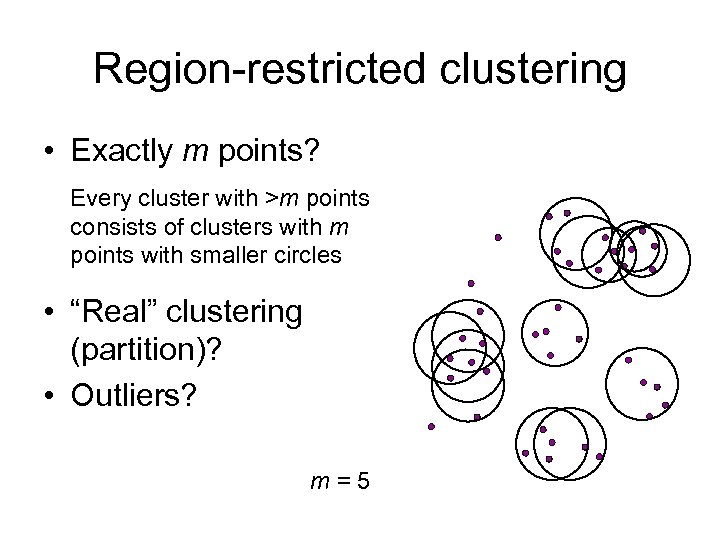 Region-restricted clustering • Exactly m points? Every cluster with >m points consists of clusters with m points with smaller circles • “Real” clustering (partition)? • Outliers? m=5
Region-restricted clustering • Exactly m points? Every cluster with >m points consists of clusters with m points with smaller circles • “Real” clustering (partition)? • Outliers? m=5
 Region-restricted clustering 1. Determine all smallest circles with m points of P inside 2. Test if the radius is ≤ r (report) or > 2 r (discard) 3. If the radius is in between, determine the area of regions of F inside
Region-restricted clustering 1. Determine all smallest circles with m points of P inside 2. Test if the radius is ≤ r (report) or > 2 r (discard) 3. If the radius is in between, determine the area of regions of F inside
 Region-restricted clustering 1. Determine all smallest circles with m points of P inside • • Use (m-2)-th order Voronoi diagram: cells where the same (m-2) points are closest Its vertices are centers of smallest circles around exactly m points
Region-restricted clustering 1. Determine all smallest circles with m points of P inside • • Use (m-2)-th order Voronoi diagram: cells where the same (m-2) points are closest Its vertices are centers of smallest circles around exactly m points
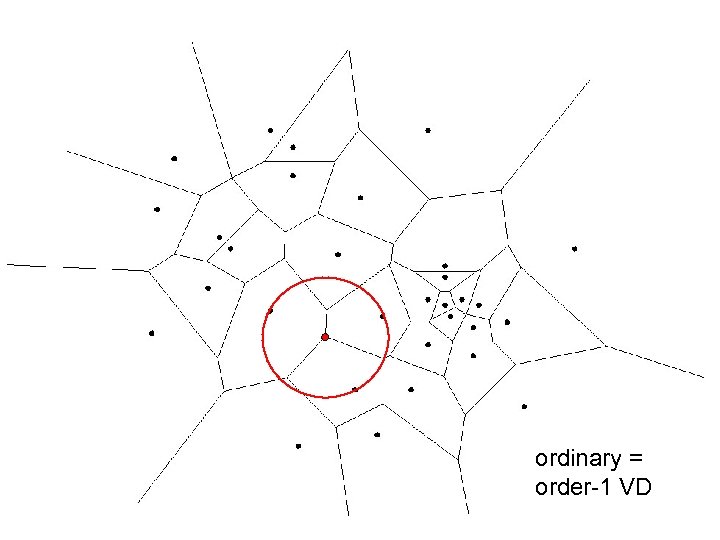 ordinary = order-1 VD
ordinary = order-1 VD
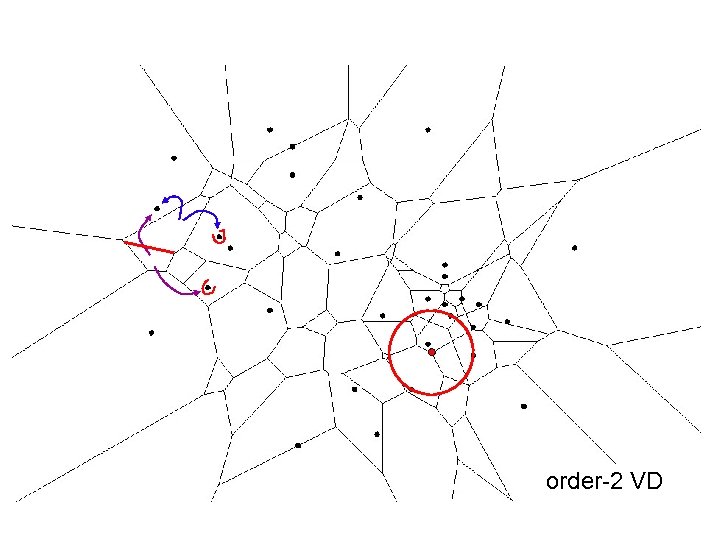 order-2 VD
order-2 VD
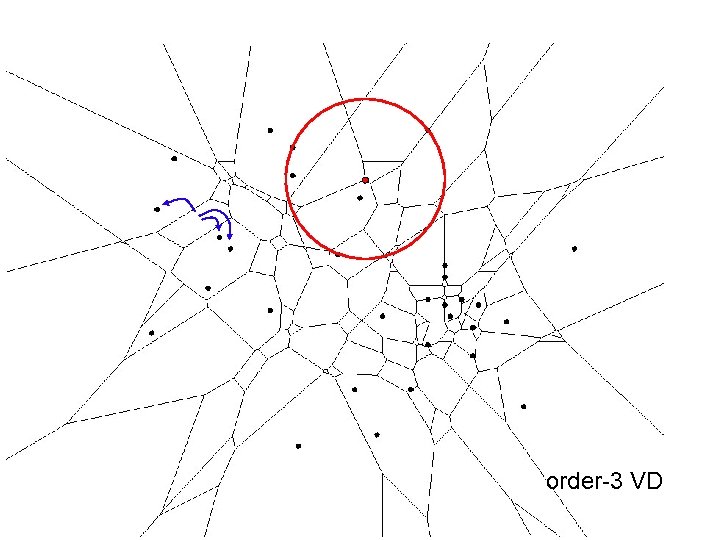 order-3 VD
order-3 VD
 Region-restricted clustering • The m-th order Voronoi diagram (or (m-2)) has O(nm) cells, edges, and vertices • It can be constructed in O(nm log n) time we get O(nm) smallest circles with m points inside; for each we also know the radius
Region-restricted clustering • The m-th order Voronoi diagram (or (m-2)) has O(nm) cells, edges, and vertices • It can be constructed in O(nm log n) time we get O(nm) smallest circles with m points inside; for each we also know the radius
 Region-restricted clustering 2. Test if the radius is ≤ r (report) or > 2 r (discard) Trivial in O(1) time per circle, so in O(nm) time overall
Region-restricted clustering 2. Test if the radius is ≤ r (report) or > 2 r (discard) Trivial in O(1) time per circle, so in O(nm) time overall
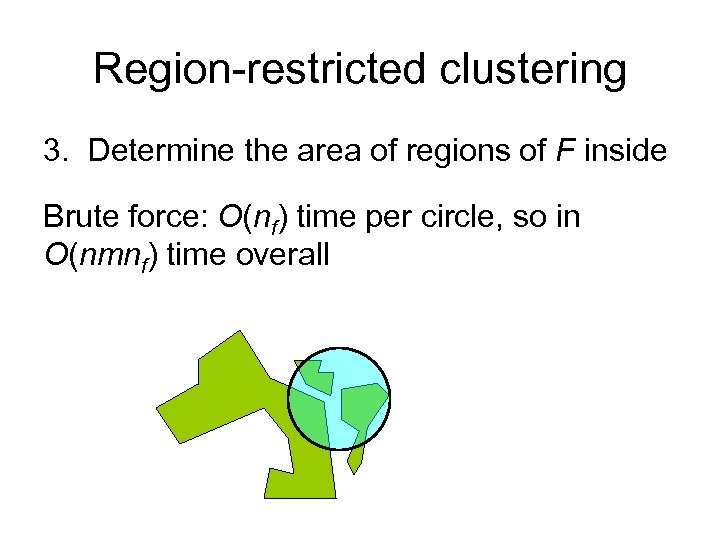 Region-restricted clustering 3. Determine the area of regions of F inside Brute force: O(nf) time per circle, so in O(nmnf) time overall
Region-restricted clustering 3. Determine the area of regions of F inside Brute force: O(nf) time per circle, so in O(nmnf) time overall
 Region-restricted clustering • Complication: This need not give all region -restricted clusters! – Need to compute area of F inside a circle with moving center – Requires solving high-degree polynomials
Region-restricted clustering • Complication: This need not give all region -restricted clusters! – Need to compute area of F inside a circle with moving center – Requires solving high-degree polynomials
 Region-restricted clusters • The anti-climax: we cannot give an exact algorithm! • If we takes squares instead of circles, we can deal with the problem. .
Region-restricted clusters • The anti-climax: we cannot give an exact algorithm! • If we takes squares instead of circles, we can deal with the problem. .
 Region-restricted clustering 3. Determine the area of regions of F inside Brute force: O(nf) time per square, so in O(nmnf) time overall The total time for steps 1, 2, and 3 is O(nm log n) + O(nmnf) = O(nm log n + nmnf) time
Region-restricted clustering 3. Determine the area of regions of F inside Brute force: O(nf) time per square, so in O(nmnf) time overall The total time for steps 1, 2, and 3 is O(nm log n) + O(nmnf) = O(nm log n + nmnf) time
 Region-restricted clustering 3. Determine the area of regions of F inside Using a suitable data structure (only possible for squares): O(log 2 nf) time per square, so in O(nm log 2 nf) time overall The total time becomes O(nm log n + nf log 2 nf + nm log 2 nf) order- (m-2) VD construction preprocessing of data structure total query time in data structure
Region-restricted clustering 3. Determine the area of regions of F inside Using a suitable data structure (only possible for squares): O(log 2 nf) time per square, so in O(nm log 2 nf) time overall The total time becomes O(nm log n + nf log 2 nf + nm log 2 nf) order- (m-2) VD construction preprocessing of data structure total query time in data structure
 Region-restricted clustering • The squares solution generalizes to regular polygons (e. g. 20 -gons) 16 -gon • An approximation of the radius within (1+ )r gives a O(n/ 2 + nf log 2 nf + n log nf /(m 2)) time algorithm
Region-restricted clustering • The squares solution generalizes to regular polygons (e. g. 20 -gons) 16 -gon • An approximation of the radius within (1+ )r gives a O(n/ 2 + nf log 2 nf + n log nf /(m 2)) time algorithm
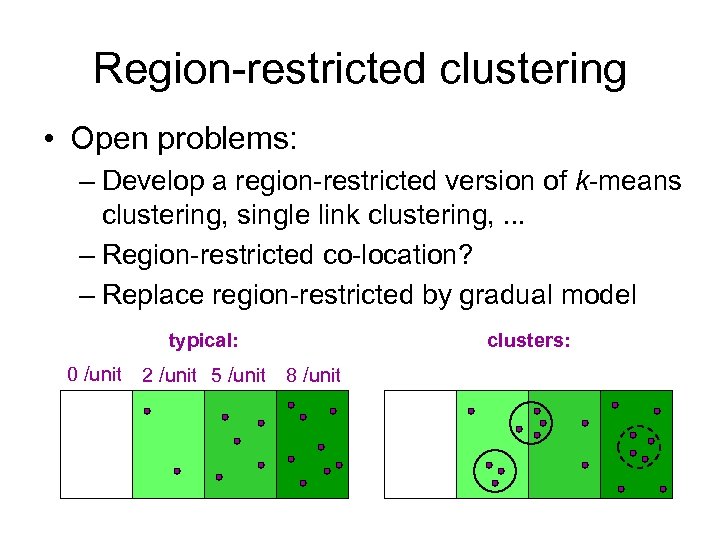 Region-restricted clustering • Open problems: – Develop a region-restricted version of k-means clustering, single link clustering, . . . – Region-restricted co-location? – Replace region-restricted by gradual model typical: 0 /unit 2 /unit 5 /unit clusters: 8 /unit
Region-restricted clustering • Open problems: – Develop a region-restricted version of k-means clustering, single link clustering, . . . – Region-restricted co-location? – Replace region-restricted by gradual model typical: 0 /unit 2 /unit 5 /unit clusters: 8 /unit
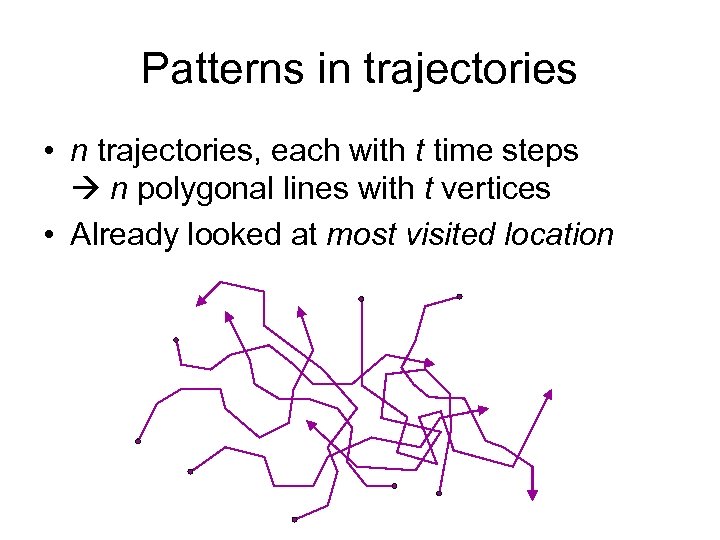 Patterns in trajectories • n trajectories, each with t time steps n polygonal lines with t vertices • Already looked at most visited location
Patterns in trajectories • n trajectories, each with t time steps n polygonal lines with t vertices • Already looked at most visited location
 Patterns in trajectories • Flock: near positions of (sub)trajectories for some subset of the entities during some time • Convergence: same destination region for some subset of the entities • Encounter: same destination region with same arrival time for some subset of the entities • Similarity of trajectories • Same direction of movement, leadership, . . . flock convergence
Patterns in trajectories • Flock: near positions of (sub)trajectories for some subset of the entities during some time • Convergence: same destination region for some subset of the entities • Encounter: same destination region with same arrival time for some subset of the entities • Similarity of trajectories • Same direction of movement, leadership, . . . flock convergence
 Patterns in trajectories • Flocking, convergence, encounter patterns – – Laube, van Kreveld, Imfeld (SDH 2004) Gudmundsson, van Kreveld, Speckmann (ACM GIS 2004) Benkert, Gudmundsson, Huebner, Wolle (ESA 2006). . . • Similarity of trajectories – Vlachos, Kollios, Gunopulos (ICDE 2002) – Shim, Chang (WAIM 2003) –. . . • Lifelines, motion mining, modeling motion – – Mountain, Raper (Geo. Computation 2001) Kollios, Scaroff, Betke (DM&KD 2001) Frank (GISDATA 8, 2001). . .
Patterns in trajectories • Flocking, convergence, encounter patterns – – Laube, van Kreveld, Imfeld (SDH 2004) Gudmundsson, van Kreveld, Speckmann (ACM GIS 2004) Benkert, Gudmundsson, Huebner, Wolle (ESA 2006). . . • Similarity of trajectories – Vlachos, Kollios, Gunopulos (ICDE 2002) – Shim, Chang (WAIM 2003) –. . . • Lifelines, motion mining, modeling motion – – Mountain, Raper (Geo. Computation 2001) Kollios, Scaroff, Betke (DM&KD 2001) Frank (GISDATA 8, 2001). . .
 Patterns in trajectories • Flock: near positions of (sub)trajectories for some subset of the entities during some time – clustering-type pattern – different definitions are used • Given: radius r, subset size m, and duration T, a flock is a subset of size m that is inside a (moving) circle of radius r for a duration T
Patterns in trajectories • Flock: near positions of (sub)trajectories for some subset of the entities during some time – clustering-type pattern – different definitions are used • Given: radius r, subset size m, and duration T, a flock is a subset of size m that is inside a (moving) circle of radius r for a duration T

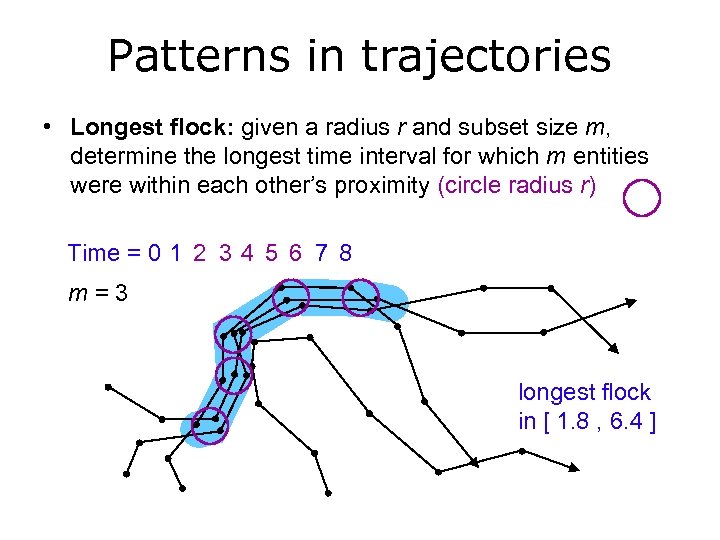 Patterns in trajectories • Longest flock: given a radius r and subset size m, determine the longest time interval for which m entities were within each other’s proximity (circle radius r) Time = 0 1 2 3 4 5 6 7 8 m=3 longest flock in [ 1. 8 , 6. 4 ]
Patterns in trajectories • Longest flock: given a radius r and subset size m, determine the longest time interval for which m entities were within each other’s proximity (circle radius r) Time = 0 1 2 3 4 5 6 7 8 m=3 longest flock in [ 1. 8 , 6. 4 ]
 Patterns in trajectories • Meet: near some position of (sub)trajectories for some subset of the entities – clustering-type pattern • Given: radius r, subset size m, and duration T, a meet is a subset of size m that is inside a (stationary) circle of radius r for a duration T this was “moving” for flock
Patterns in trajectories • Meet: near some position of (sub)trajectories for some subset of the entities – clustering-type pattern • Given: radius r, subset size m, and duration T, a meet is a subset of size m that is inside a (stationary) circle of radius r for a duration T this was “moving” for flock

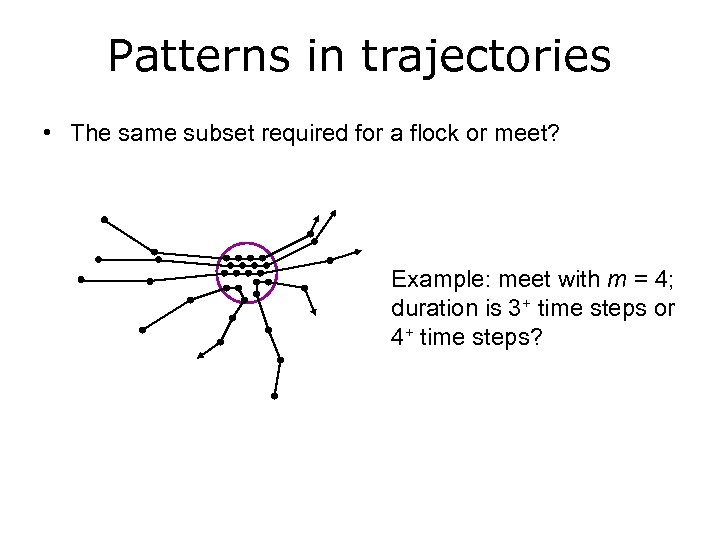 Patterns in trajectories • The same subset required for a flock or meet? Example: meet with m = 4; duration is 3+ time steps or 4+ time steps?
Patterns in trajectories • The same subset required for a flock or meet? Example: meet with m = 4; duration is 3+ time steps or 4+ time steps?
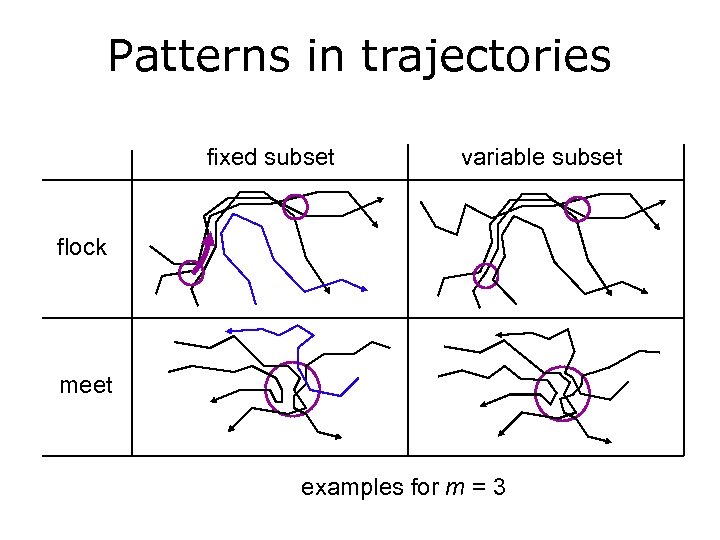 Patterns in trajectories fixed subset variable subset flock meet examples for m = 3
Patterns in trajectories fixed subset variable subset flock meet examples for m = 3
 Patterns in trajectories fixed subset flock meet NP-hard O(n 4 2 log n + n 2 3) variable subset O(n 3 log n) O(n 4 2 log n + n 2 3) Exact results ( input size is n )
Patterns in trajectories fixed subset flock meet NP-hard O(n 4 2 log n + n 2 3) variable subset O(n 3 log n) O(n 4 2 log n + n 2 3) Exact results ( input size is n )
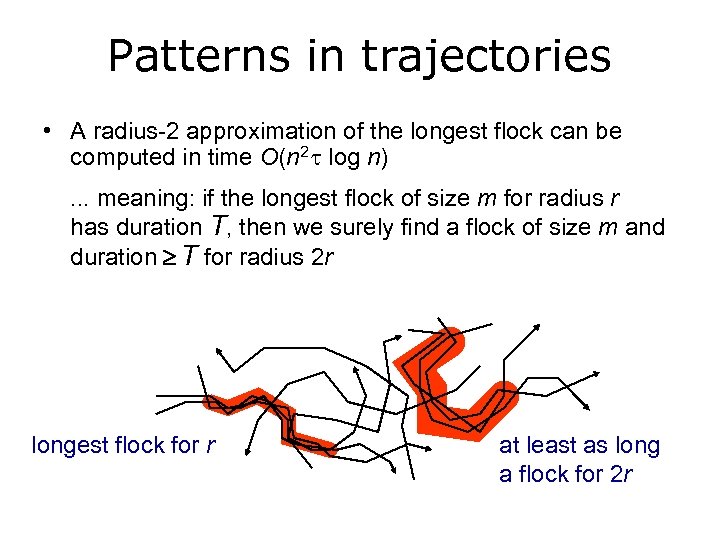 Patterns in trajectories • A radius-2 approximation of the longest flock can be computed in time O(n 2 log n). . . meaning: if the longest flock of size m for radius r has duration T, then we surely find a flock of size m and duration T for radius 2 r longest flock for r at least as long a flock for 2 r
Patterns in trajectories • A radius-2 approximation of the longest flock can be computed in time O(n 2 log n). . . meaning: if the longest flock of size m for radius r has duration T, then we surely find a flock of size m and duration T for radius 2 r longest flock for r at least as long a flock for 2 r
 Patterns in trajectories Approximate radius results ( input size is n ) fixed subset flock O(n 2 log n) variable subset O((n 2 log n) / 2) factor 2 NP-hard meet factor 2+ O(n 3 log n) O((n 2 log n) / (m 2)) factor 1+ O(n 4 2 log n + n 2 3)
Patterns in trajectories Approximate radius results ( input size is n ) fixed subset flock O(n 2 log n) variable subset O((n 2 log n) / 2) factor 2 NP-hard meet factor 2+ O(n 3 log n) O((n 2 log n) / (m 2)) factor 1+ O(n 4 2 log n + n 2 3)
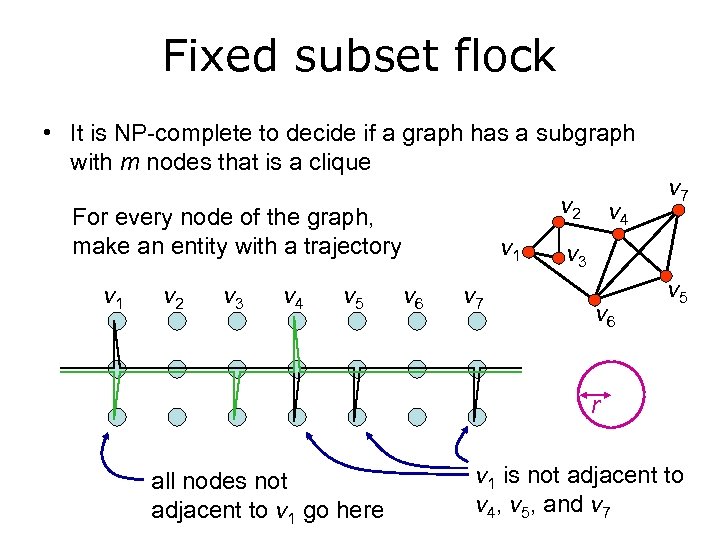 Fixed subset flock • It is NP-complete to decide if a graph has a subgraph with m nodes that is a clique v 2 For every node of the graph, make an entity with a trajectory v 1 v 2 v 3 v 4 v 5 v 1 v 6 v 7 v 4 v 7 v 3 v 6 v 5 r all nodes not adjacent to v 1 go here v 1 is not adjacent to v 4, v 5, and v 7
Fixed subset flock • It is NP-complete to decide if a graph has a subgraph with m nodes that is a clique v 2 For every node of the graph, make an entity with a trajectory v 1 v 2 v 3 v 4 v 5 v 1 v 6 v 7 v 4 v 7 v 3 v 6 v 5 r all nodes not adjacent to v 1 go here v 1 is not adjacent to v 4, v 5, and v 7
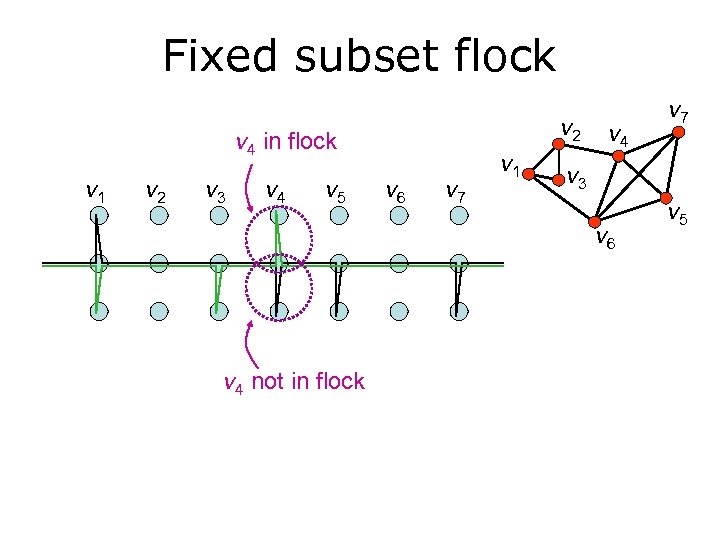 Fixed subset flock v 2 v 4 in flock v 1 v 2 v 3 v 4 v 5 v 6 v 7 v 1 v 4 v 3 v 6 v 4 not in flock v 7 v 5
Fixed subset flock v 2 v 4 in flock v 1 v 2 v 3 v 4 v 5 v 6 v 7 v 1 v 4 v 3 v 6 v 4 not in flock v 7 v 5
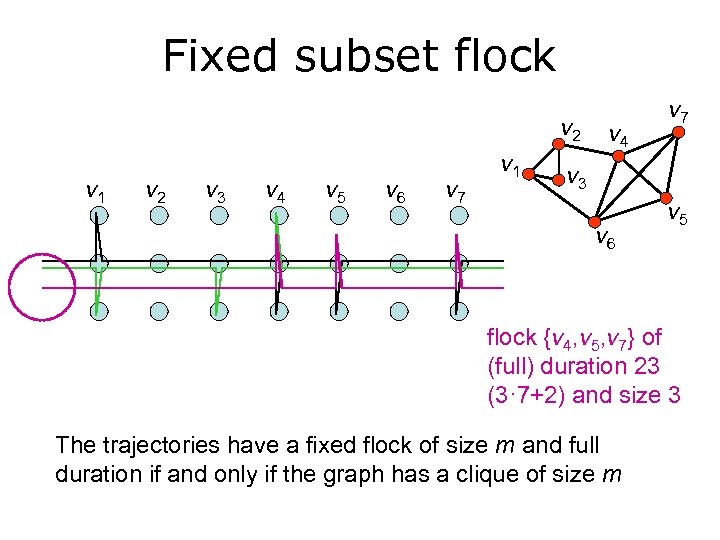 Fixed subset flock v 2 v 1 v 2 v 3 v 4 v 5 v 6 v 7 v 1 v 4 v 7 v 3 v 6 v 5 flock {v 4, v 5, v 7} of (full) duration 23 (3· 7+2) and size 3 The trajectories have a fixed flock of size m and full duration if and only if the graph has a clique of size m
Fixed subset flock v 2 v 1 v 2 v 3 v 4 v 5 v 6 v 7 v 1 v 4 v 7 v 3 v 6 v 5 flock {v 4, v 5, v 7} of (full) duration 23 (3· 7+2) and size 3 The trajectories have a fixed flock of size m and full duration if and only if the graph has a clique of size m
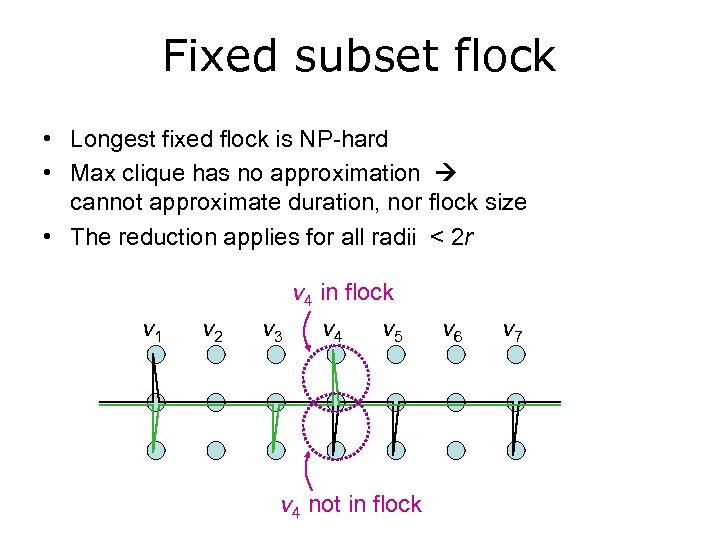 Fixed subset flock • Longest fixed flock is NP-hard • Max clique has no approximation cannot approximate duration, nor flock size • The reduction applies for all radii < 2 r v 1 v 2 v 4 in flock v 3 v 4 v 5 v 4 not in flock v 6 v 7
Fixed subset flock • Longest fixed flock is NP-hard • Max clique has no approximation cannot approximate duration, nor flock size • The reduction applies for all radii < 2 r v 1 v 2 v 4 in flock v 3 v 4 v 5 v 4 not in flock v 6 v 7
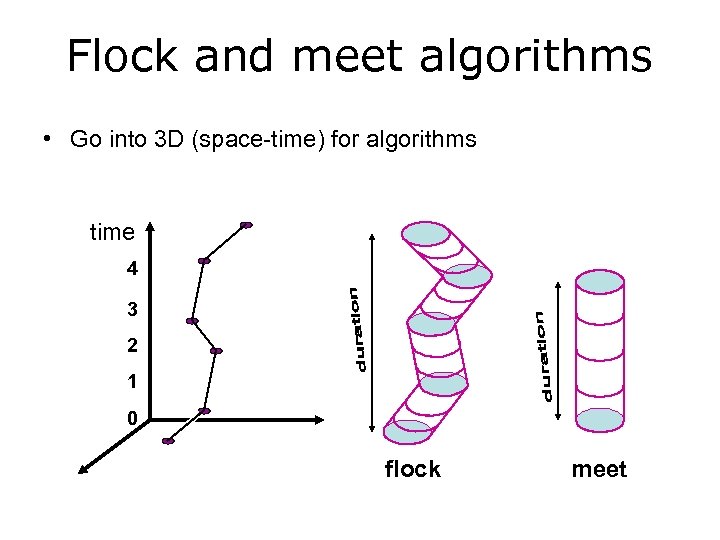 Flock and meet algorithms • Go into 3 D (space-time) for algorithms time 4 3 2 1 0 flock meet
Flock and meet algorithms • Go into 3 D (space-time) for algorithms time 4 3 2 1 0 flock meet
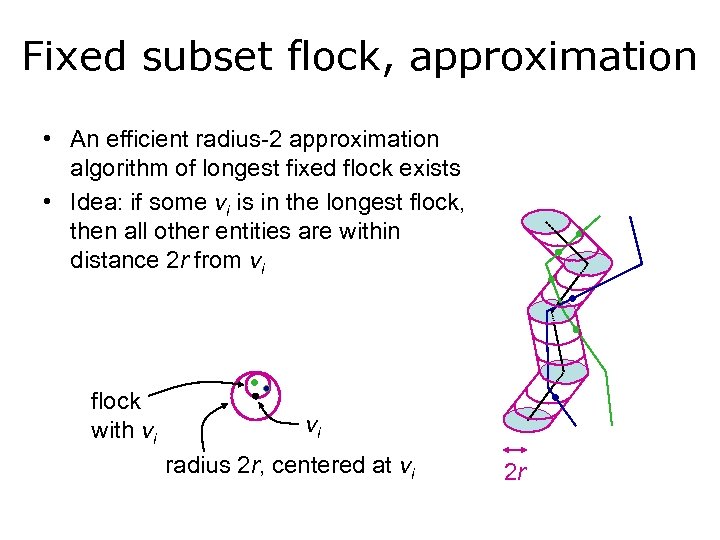 Fixed subset flock, approximation • An efficient radius-2 approximation algorithm of longest fixed flock exists • Idea: if some vi is in the longest flock, then all other entities are within distance 2 r from vi flock with vi vi radius 2 r, centered at vi 2 r
Fixed subset flock, approximation • An efficient radius-2 approximation algorithm of longest fixed flock exists • Idea: if some vi is in the longest flock, then all other entities are within distance 2 r from vi flock with vi vi radius 2 r, centered at vi 2 r
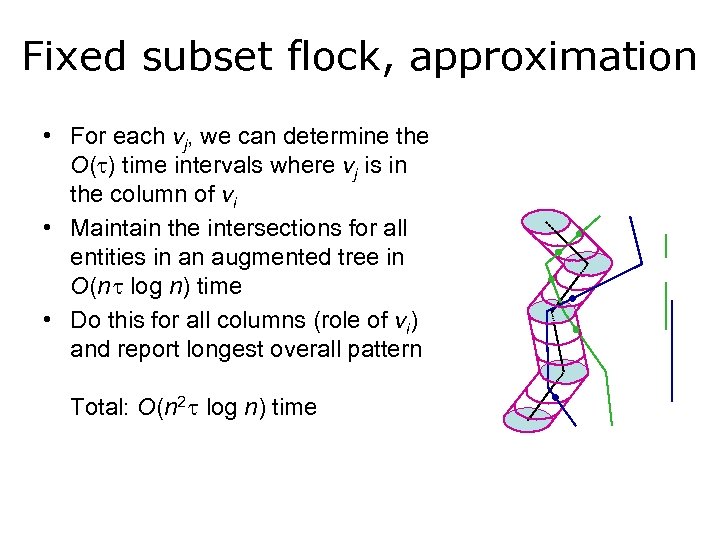 Fixed subset flock, approximation • For each vj, we can determine the O( ) time intervals where vj is in the column of vi • Maintain the intersections for all entities in an augmented tree in O(n log n) time • Do this for all columns (role of vi) and report longest overall pattern Total: O(n 2 log n) time
Fixed subset flock, approximation • For each vj, we can determine the O( ) time intervals where vj is in the column of vi • Maintain the intersections for all entities in an augmented tree in O(n log n) time • Do this for all columns (role of vi) and report longest overall pattern Total: O(n 2 log n) time
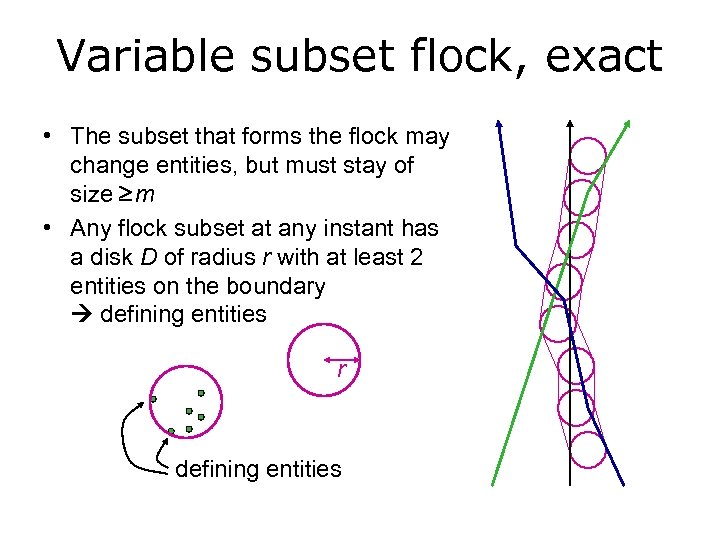 Variable subset flock, exact • The subset that forms the flock may change entities, but must stay of size m • Any flock subset at any instant has a disk D of radius r with at least 2 entities on the boundary defining entities r defining entities
Variable subset flock, exact • The subset that forms the flock may change entities, but must stay of size m • Any flock subset at any instant has a disk D of radius r with at least 2 entities on the boundary defining entities r defining entities
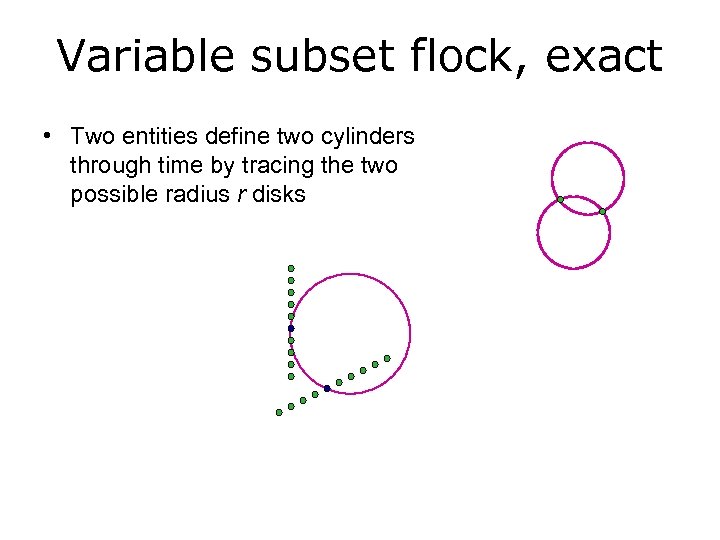
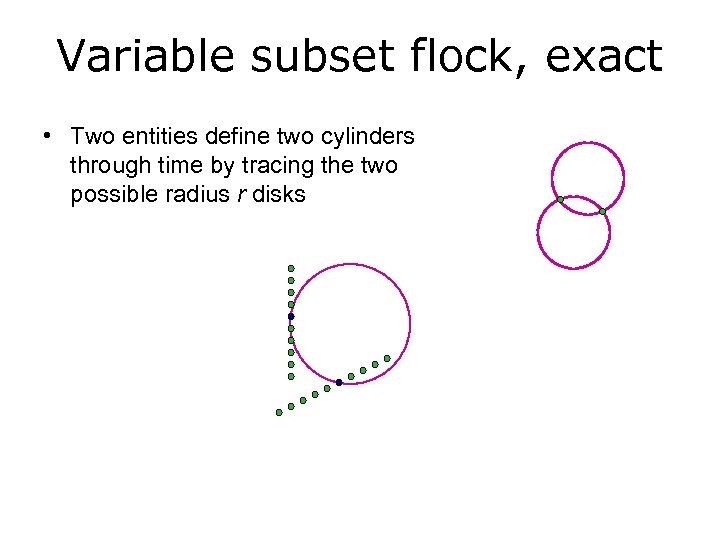
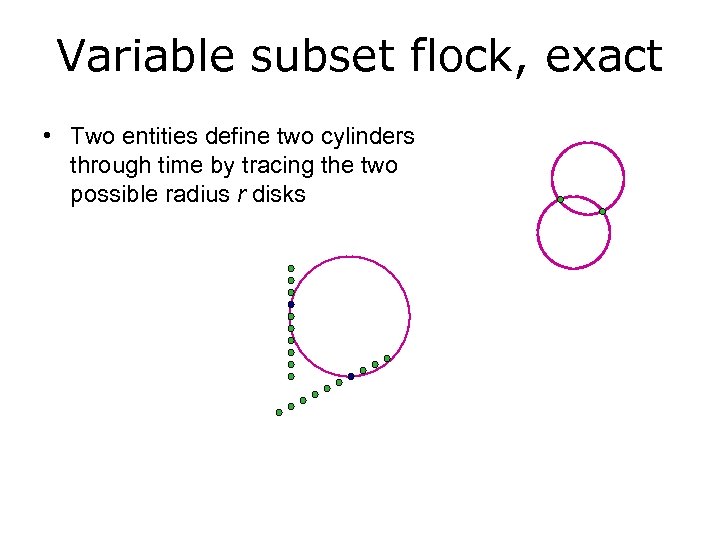
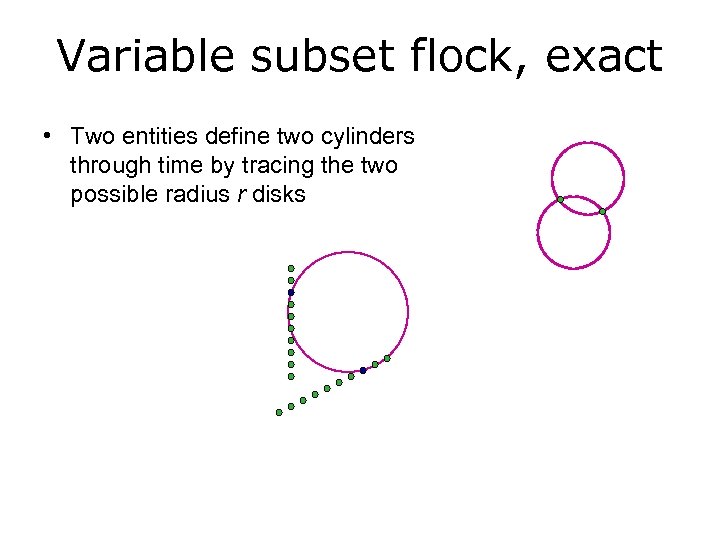
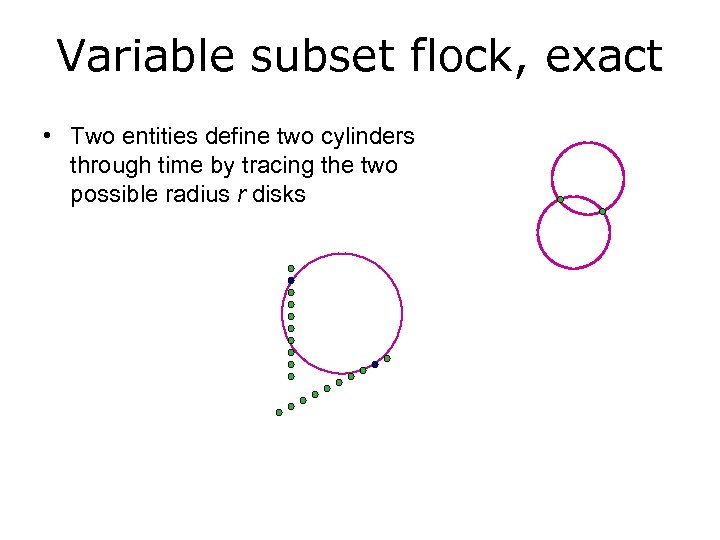
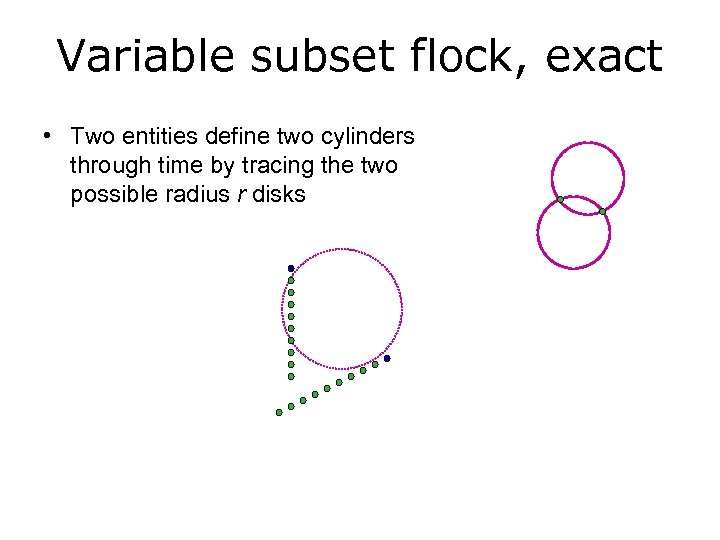
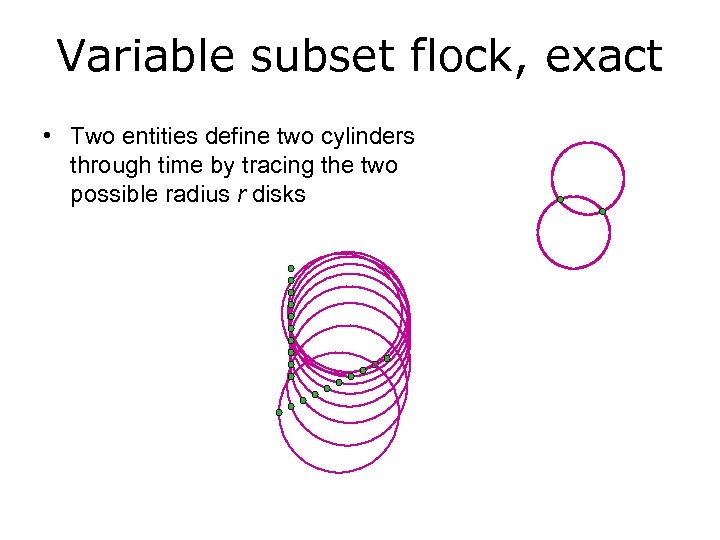
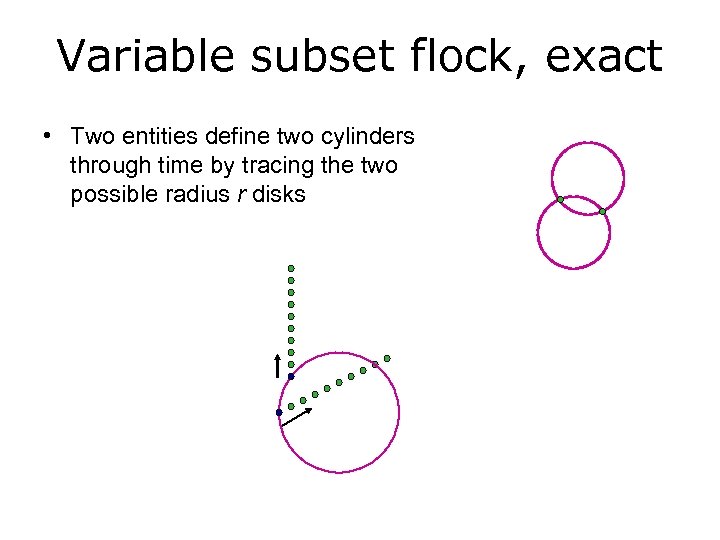 Variable subset flock, exact • Two entities define two cylinders through time by tracing the two possible radius r disks
Variable subset flock, exact • Two entities define two cylinders through time by tracing the two possible radius r disks
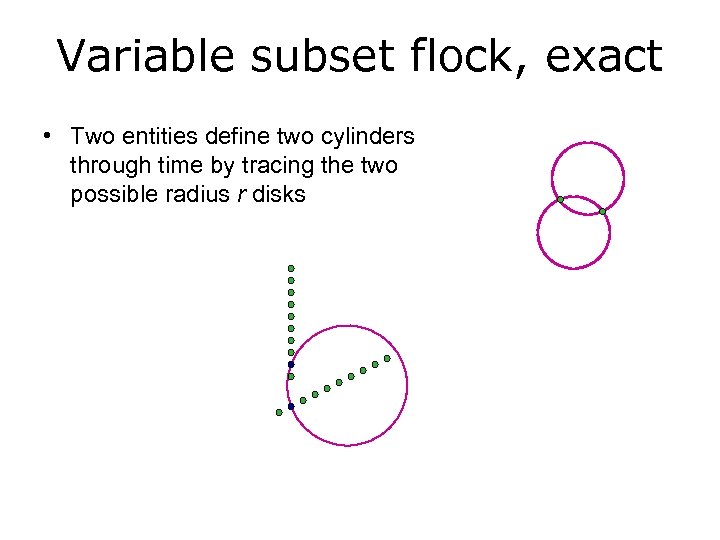 Variable subset flock, exact • Two entities define two cylinders through time by tracing the two possible radius r disks
Variable subset flock, exact • Two entities define two cylinders through time by tracing the two possible radius r disks
 Variable subset flock, exact • Two entities define two cylinders through time by tracing the two possible radius r disks
Variable subset flock, exact • Two entities define two cylinders through time by tracing the two possible radius r disks
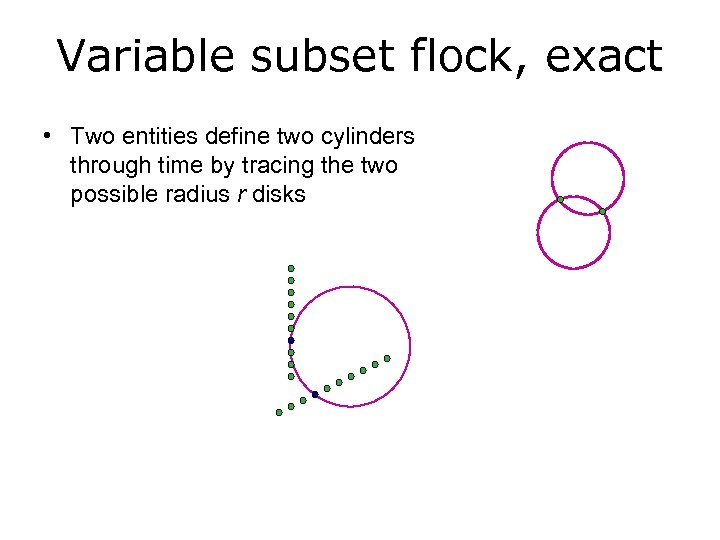 Variable subset flock, exact • Two entities define two cylinders through time by tracing the two possible radius r disks
Variable subset flock, exact • Two entities define two cylinders through time by tracing the two possible radius r disks
 Variable subset flock, exact • Two entities define two cylinders through time by tracing the two possible radius r disks
Variable subset flock, exact • Two entities define two cylinders through time by tracing the two possible radius r disks
 Variable subset flock, exact • Two entities define two cylinders through time by tracing the two possible radius r disks
Variable subset flock, exact • Two entities define two cylinders through time by tracing the two possible radius r disks
 Variable subset flock, exact • Two entities define two cylinders through time by tracing the two possible radius r disks
Variable subset flock, exact • Two entities define two cylinders through time by tracing the two possible radius r disks
 Variable subset flock, exact • Two entities define two cylinders through time by tracing the two possible radius r disks
Variable subset flock, exact • Two entities define two cylinders through time by tracing the two possible radius r disks
 Variable subset flock, exact • Two entities define two cylinders through time by tracing the two possible radius r disks
Variable subset flock, exact • Two entities define two cylinders through time by tracing the two possible radius r disks
 Variable subset flock, exact • Two entities define two cylinders through time by tracing the two possible radius r disks
Variable subset flock, exact • Two entities define two cylinders through time by tracing the two possible radius r disks
 Variable subset flock, exact • Two entities define two cylinders through time by tracing the two possible radius r disks
Variable subset flock, exact • Two entities define two cylinders through time by tracing the two possible radius r disks
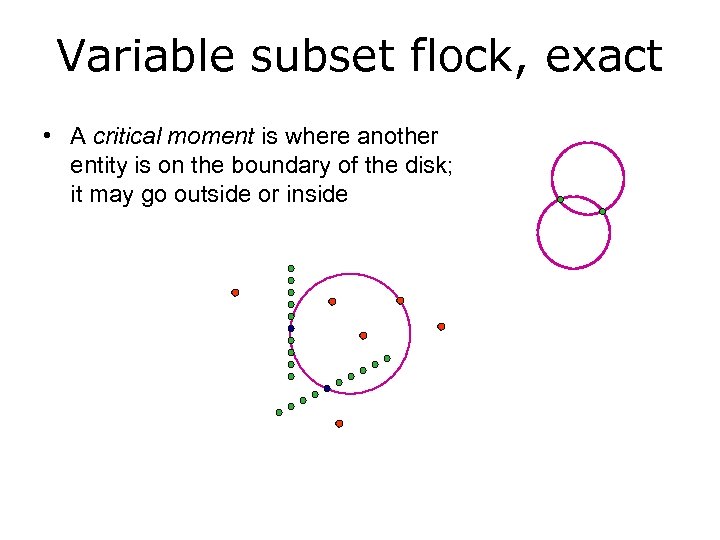 Variable subset flock, exact • A critical moment is where another entity is on the boundary of the disk; it may go outside or inside
Variable subset flock, exact • A critical moment is where another entity is on the boundary of the disk; it may go outside or inside
 Variable subset flock, exact • At a critical moment: – a variable subset flock may start (m entities) – a variable subset flock may stop (
Variable subset flock, exact • At a critical moment: – a variable subset flock may start (m entities) – a variable subset flock may stop (
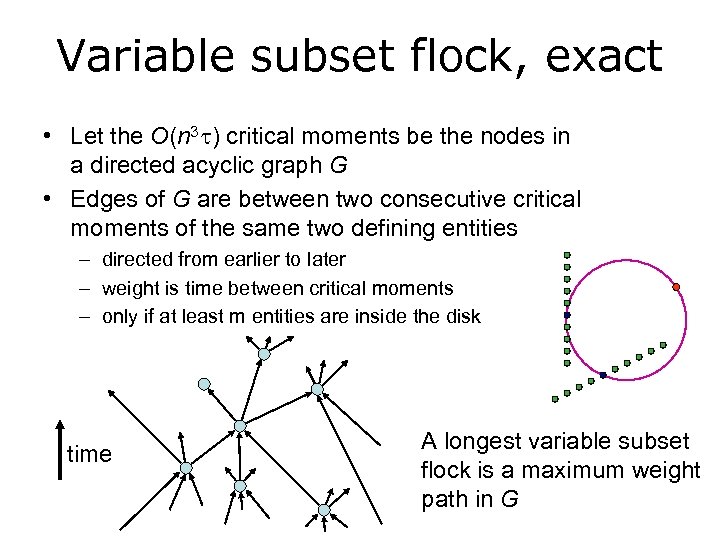 Variable subset flock, exact • Let the O(n 3 ) critical moments be the nodes in a directed acyclic graph G • Edges of G are between two consecutive critical moments of the same two defining entities – directed from earlier to later – weight is time between critical moments – only if at least m entities are inside the disk time A longest variable subset flock is a maximum weight path in G
Variable subset flock, exact • Let the O(n 3 ) critical moments be the nodes in a directed acyclic graph G • Edges of G are between two consecutive critical moments of the same two defining entities – directed from earlier to later – weight is time between critical moments – only if at least m entities are inside the disk time A longest variable subset flock is a maximum weight path in G
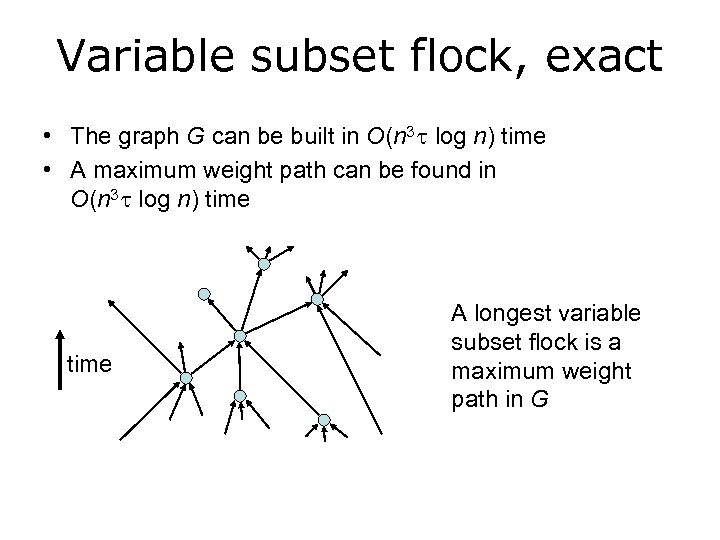 Variable subset flock, exact • The graph G can be built in O(n 3 log n) time • A maximum weight path can be found in O(n 3 log n) time A longest variable subset flock is a maximum weight path in G
Variable subset flock, exact • The graph G can be built in O(n 3 log n) time • A maximum weight path can be found in O(n 3 log n) time A longest variable subset flock is a maximum weight path in G
 Patterns in trajectories, summary • Flock and meet patterns require algorithms in 3 dimensional space (space-time) • Exact algorithms are inefficient only suitable for smaller data sets • Approximation can reduce running time with one or two orders of magnitude
Patterns in trajectories, summary • Flock and meet patterns require algorithms in 3 dimensional space (space-time) • Exact algorithms are inefficient only suitable for smaller data sets • Approximation can reduce running time with one or two orders of magnitude
 Patterns in trajectories, summary fixed subset apx flock exact O(n 2 log n) factor 2 NP-hard variable subset O((n 2 log n) / 2) factor 2+ O(n 3 log n) apx O((n 2 log n) / (m 2)) factor 1+ meet exact O(n 4 2 log n + n 2 3)
Patterns in trajectories, summary fixed subset apx flock exact O(n 2 log n) factor 2 NP-hard variable subset O((n 2 log n) / 2) factor 2+ O(n 3 log n) apx O((n 2 log n) / (m 2)) factor 1+ meet exact O(n 4 2 log n + n 2 3)
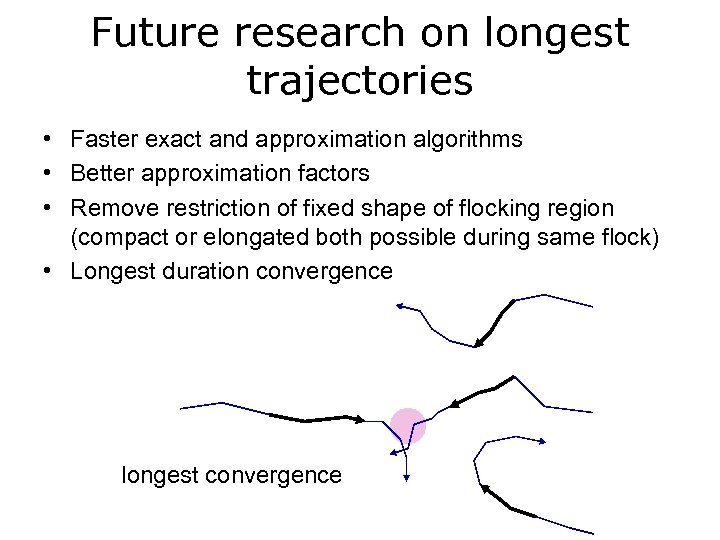 Future research on longest trajectories • Faster exact and approximation algorithms • Better approximation factors • Remove restriction of fixed shape of flocking region (compact or elongated both possible during same flock) • Longest duration convergence longest convergence
Future research on longest trajectories • Faster exact and approximation algorithms • Better approximation factors • Remove restriction of fixed shape of flocking region (compact or elongated both possible during same flock) • Longest duration convergence longest convergence
 Patterns in trajectories • Flock and meet patterns require algorithms in 3 dimensional space (space-time) • Exact algorithms are inefficient only suitable for smaller data sets • Approximation can reduce running time with an order of magnitude
Patterns in trajectories • Flock and meet patterns require algorithms in 3 dimensional space (space-time) • Exact algorithms are inefficient only suitable for smaller data sets • Approximation can reduce running time with an order of magnitude
 To conclude • With an exact definition of a spatial or spatiotemporal pattern, geometric algorithms can be used to compute all patterns • Many known structures from computational geometry are useful (Voronoi diagrams, arrangements, . . . ) • Since the (exact) algorithms may be inefficient, approximation may be a solution
To conclude • With an exact definition of a spatial or spatiotemporal pattern, geometric algorithms can be used to compute all patterns • Many known structures from computational geometry are useful (Voronoi diagrams, arrangements, . . . ) • Since the (exact) algorithms may be inefficient, approximation may be a solution
 To discuss • What patterns must be detected in practice (both spatial and spatio-temporal)? • What is the most appropriate definition (formalization) of these? • Spatial association rules, auto-correlation, irregularities, classification, . . . and other computable things in spatial/spatio-temporal data mining
To discuss • What patterns must be detected in practice (both spatial and spatio-temporal)? • What is the most appropriate definition (formalization) of these? • Spatial association rules, auto-correlation, irregularities, classification, . . . and other computable things in spatial/spatio-temporal data mining


