793354170d376f004d47d97f76469427.ppt
- Количество слайдов: 34

 Computational Fluid Dynamic (CFD) Analysis of Gas and Liquid Flow Through a Modular Sample System Tony Y. Bougebrayel, PE, Ph. D John J. Wawrowski Swagelok Solon, Ohio IFPAC 2003 Scottsdale, Az January 21 -24, 2003 © Swagelok Company, 2002
Computational Fluid Dynamic (CFD) Analysis of Gas and Liquid Flow Through a Modular Sample System Tony Y. Bougebrayel, PE, Ph. D John J. Wawrowski Swagelok Solon, Ohio IFPAC 2003 Scottsdale, Az January 21 -24, 2003 © Swagelok Company, 2002
 Agenda Objective Cv, K Factor CFD Background MPC - CFD Model Description, Procedure Results Conclusions © Swagelok Company, 2002
Agenda Objective Cv, K Factor CFD Background MPC - CFD Model Description, Procedure Results Conclusions © Swagelok Company, 2002
 Objectives Evaluate the flow capacity (Cv) for a threeposition Swagelok MPC substrate flow component Investigate the effects of using different surfacemount components on the total system Cv Determine an analytical method for predicting the total system Cv Investigate the effect of the fluid type on the pressure drop through a substrate flow component Determine the pressure required to flow a liquid sample through a Swagelok MPC system © Swagelok Company, 2002
Objectives Evaluate the flow capacity (Cv) for a threeposition Swagelok MPC substrate flow component Investigate the effects of using different surfacemount components on the total system Cv Determine an analytical method for predicting the total system Cv Investigate the effect of the fluid type on the pressure drop through a substrate flow component Determine the pressure required to flow a liquid sample through a Swagelok MPC system © Swagelok Company, 2002
 Cv and K Factors The Cv Approach The K Approach What causes Cv and K and how are they determined? How do they relate to the MPC? © Swagelok Company, 2002
Cv and K Factors The Cv Approach The K Approach What causes Cv and K and how are they determined? How do they relate to the MPC? © Swagelok Company, 2002
 The Cv Approach Cv: Flow capacity (component) For Newtonian Liquids: Through control components: q = N 1 * Fp * Cv * (Δp / Gf)1/2 (ISA 75. 01) Through straight pipes: Δp =. 000216 f L Q 2 / d 5 (Darcy’s) For Gases: Through control components: q = N 7 * Fp * Cv * p 1 * Y * [x / (Gg T 1 Z)]1/2 (ISA 75. 01) For Low pressure drop: 1. 0 < Y < 2/3, (p 1 2 p 2) and Y = 1 – x / (3 Fk xt) For high pressure flow (choked flow, p 1>2 p 2): Y= 2/3, xt=. 5 and q = N 7 * Fp * Cv * p 1*. 471*[1 / T 1 Z)]1/2 © Swagelok Company, 2002
The Cv Approach Cv: Flow capacity (component) For Newtonian Liquids: Through control components: q = N 1 * Fp * Cv * (Δp / Gf)1/2 (ISA 75. 01) Through straight pipes: Δp =. 000216 f L Q 2 / d 5 (Darcy’s) For Gases: Through control components: q = N 7 * Fp * Cv * p 1 * Y * [x / (Gg T 1 Z)]1/2 (ISA 75. 01) For Low pressure drop: 1. 0 < Y < 2/3, (p 1 2 p 2) and Y = 1 – x / (3 Fk xt) For high pressure flow (choked flow, p 1>2 p 2): Y= 2/3, xt=. 5 and q = N 7 * Fp * Cv * p 1*. 471*[1 / T 1 Z)]1/2 © Swagelok Company, 2002
 The K Approach K-Factor: Resistance to flow (system) Head loss through a pipe, valve, or fitting: h. L = K v 2 / 2 g where: K = f L / D (Darcy’s) Bernoulli’s equation (mechanical energy): z 1 + 144 p 1/ 1 + v 12/2 g = z 2 + 144 p 2/ 2 + v 22/2 g + h. L Potential Energy Pressure Kinetic Total Energy Head Loss © Swagelok Company, 2002
The K Approach K-Factor: Resistance to flow (system) Head loss through a pipe, valve, or fitting: h. L = K v 2 / 2 g where: K = f L / D (Darcy’s) Bernoulli’s equation (mechanical energy): z 1 + 144 p 1/ 1 + v 12/2 g = z 2 + 144 p 2/ 2 + v 22/2 g + h. L Potential Energy Pressure Kinetic Total Energy Head Loss © Swagelok Company, 2002
 The Make-up of Cv and K Changes in the flow direction (turns) Changes in the geometry (expansion, contraction, flow obstacles) Geometry size Weight of the fluid (density effects) Velocity of approach (entry and exit velocity) Friction between the fluid and solid as well as within the fluid layers (viscosity effects) Elevation (1 psi is about 27. 8 inches of water head) © Swagelok Company, 2002
The Make-up of Cv and K Changes in the flow direction (turns) Changes in the geometry (expansion, contraction, flow obstacles) Geometry size Weight of the fluid (density effects) Velocity of approach (entry and exit velocity) Friction between the fluid and solid as well as within the fluid layers (viscosity effects) Elevation (1 psi is about 27. 8 inches of water head) © Swagelok Company, 2002
 The Make-up of Cv and K — Order of Importance 1. Transition: A sharp 90 -degree turn costs the flow more energy (pressure) than the frictional losses or pipe reduction losses (i. e. losses due to a short 90 deg. turn are four times greater than losses due to a half size reduction in the pipe diameter) 2. Pipe Size: Pipe size reduction has a 5 -power effect on the flow where the frictional losses are at 1 st order 3. Friction: The frictional losses are of greater relative importance in smaller components (frictional losses decrease with the increase in flow velocity or pipe diameter) © Swagelok Company, 2002
The Make-up of Cv and K — Order of Importance 1. Transition: A sharp 90 -degree turn costs the flow more energy (pressure) than the frictional losses or pipe reduction losses (i. e. losses due to a short 90 deg. turn are four times greater than losses due to a half size reduction in the pipe diameter) 2. Pipe Size: Pipe size reduction has a 5 -power effect on the flow where the frictional losses are at 1 st order 3. Friction: The frictional losses are of greater relative importance in smaller components (frictional losses decrease with the increase in flow velocity or pipe diameter) © Swagelok Company, 2002
 How are Cv and K determined? Testing (ISA 75. 02) Empirical values (macroscopic approach) CFD (microscopic approach) © Swagelok Company, 2002
How are Cv and K determined? Testing (ISA 75. 02) Empirical values (macroscopic approach) CFD (microscopic approach) © Swagelok Company, 2002
 Computational Fluid Dynamics — Background CFD History How it works Swagelok’s Effort © Swagelok Company, 2002
Computational Fluid Dynamics — Background CFD History How it works Swagelok’s Effort © Swagelok Company, 2002
 CFD History Scientific community (space research and power production) Current Status and Applications Challenges © Swagelok Company, 2002
CFD History Scientific community (space research and power production) Current Status and Applications Challenges © Swagelok Company, 2002
 How Does CFD Work? Geometry Mesh Boundary Conditions Solution Method Post Processing © Swagelok Company, 2002
How Does CFD Work? Geometry Mesh Boundary Conditions Solution Method Post Processing © Swagelok Company, 2002
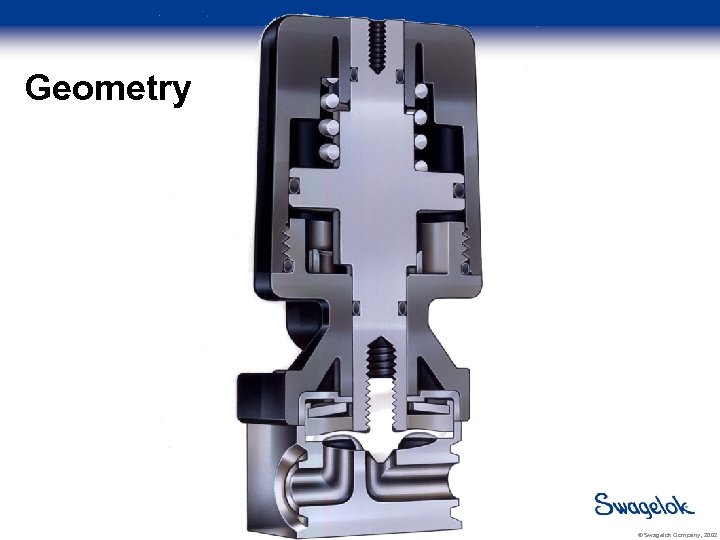 Geometry © Swagelok Company, 2002
Geometry © Swagelok Company, 2002
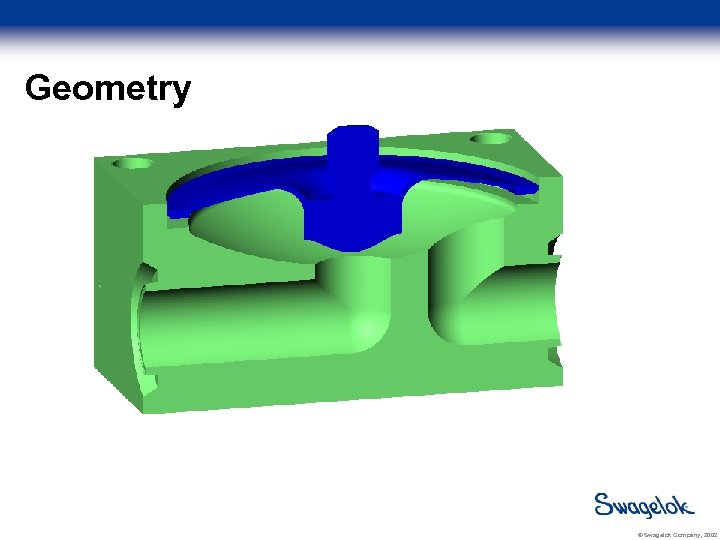 Geometry © Swagelok Company, 2002
Geometry © Swagelok Company, 2002
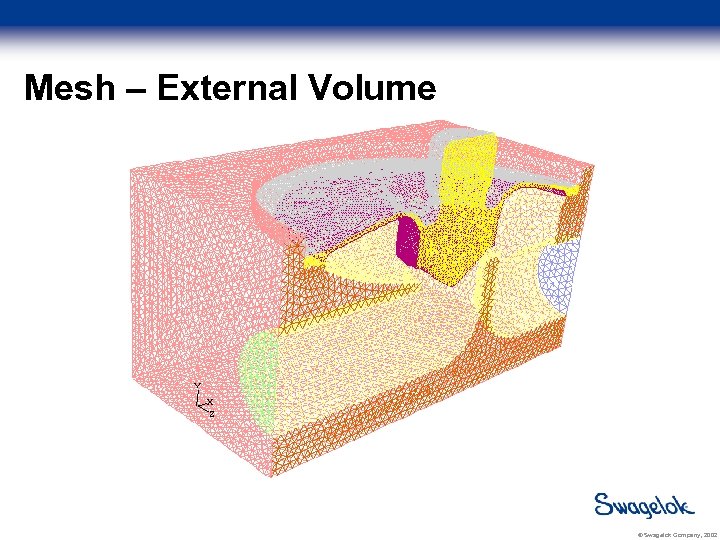 Mesh – External Volume © Swagelok Company, 2002
Mesh – External Volume © Swagelok Company, 2002
 Mesh – Internal Volume © Swagelok Company, 2002
Mesh – Internal Volume © Swagelok Company, 2002
 Boundary Conditions Mass Flow Rate Pressure Velocity Inlet-Vent Inlet-fan © Swagelok Company, 2002
Boundary Conditions Mass Flow Rate Pressure Velocity Inlet-Vent Inlet-fan © Swagelok Company, 2002
 Solution Method Coupled/Segregated Laminar/Turbulent K- , RSM, k- , LES, … Compressible/Incompressible Steady State/Transient Set the Boundary Conditions Initialize the Solution Solve © Swagelok Company, 2002
Solution Method Coupled/Segregated Laminar/Turbulent K- , RSM, k- , LES, … Compressible/Incompressible Steady State/Transient Set the Boundary Conditions Initialize the Solution Solve © Swagelok Company, 2002
 Post Processing © Swagelok Company, 2002
Post Processing © Swagelok Company, 2002
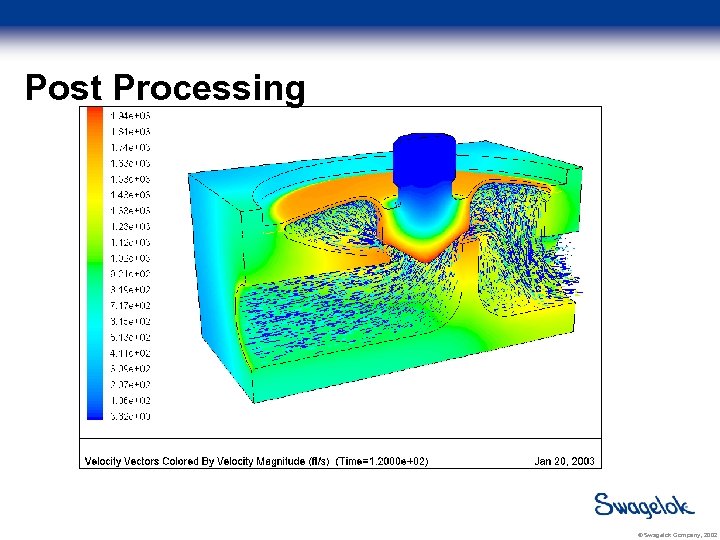 Post Processing © Swagelok Company, 2002
Post Processing © Swagelok Company, 2002
 Post Processing © Swagelok Company, 2002
Post Processing © Swagelok Company, 2002
 Swagelok’s Effort Swagelok gained in-house CFD capabilities in 1997 The majority of applications revolve around finding/optimizing Cv and Heat transfer analysis Swagelok tool box: Fluent®, Floworks®, and Pipeflow® © Swagelok Company, 2002
Swagelok’s Effort Swagelok gained in-house CFD capabilities in 1997 The majority of applications revolve around finding/optimizing Cv and Heat transfer analysis Swagelok tool box: Fluent®, Floworks®, and Pipeflow® © Swagelok Company, 2002
 MPC – CFD Model © Swagelok Company, 2002
MPC – CFD Model © Swagelok Company, 2002
 MPC - CFD Model: Turbulent, Steady State, Segregated, Implicit Geometry: 3 D with symmetry about the center plane Viscous Model: Standard k- turbulence model Medium: Water, Air and some Hydrocarbons Boundary Conditions: Inlet: Mass Flow Rate (300 ml/min) Outlet: Atmospheric pressure Mesh: Hybrid, 120 k order Convergence Criteria: Conservation of mass, Y+ © Swagelok Company, 2002
MPC - CFD Model: Turbulent, Steady State, Segregated, Implicit Geometry: 3 D with symmetry about the center plane Viscous Model: Standard k- turbulence model Medium: Water, Air and some Hydrocarbons Boundary Conditions: Inlet: Mass Flow Rate (300 ml/min) Outlet: Atmospheric pressure Mesh: Hybrid, 120 k order Convergence Criteria: Conservation of mass, Y+ © Swagelok Company, 2002
 Results Cv of a three-position system © Swagelok Company, 2002
Results Cv of a three-position system © Swagelok Company, 2002
 Results Predicted Cv: 0. 040 Tested Cv: 0. 045 Flow Direction © Swagelok Company, 2002
Results Predicted Cv: 0. 040 Tested Cv: 0. 045 Flow Direction © Swagelok Company, 2002
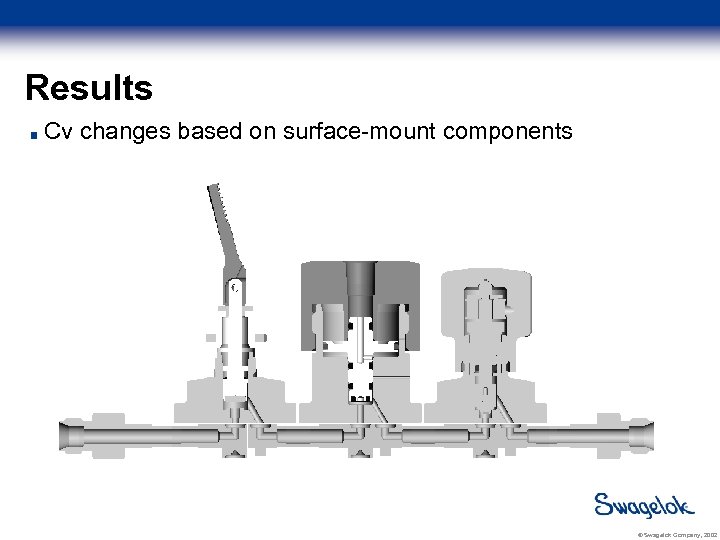 Results Cv changes based on surface-mount components © Swagelok Company, 2002
Results Cv changes based on surface-mount components © Swagelok Company, 2002
 Results Total system Cv: 1/Cvtotal 2 = Σ (1/Cvi)2 Cv 1 Cv 2 Cv 3 Cv 4 Cv 5 Cv 6 Cv 7 Flow Direction © Swagelok Company, 2002
Results Total system Cv: 1/Cvtotal 2 = Σ (1/Cvi)2 Cv 1 Cv 2 Cv 3 Cv 4 Cv 5 Cv 6 Cv 7 Flow Direction © Swagelok Company, 2002
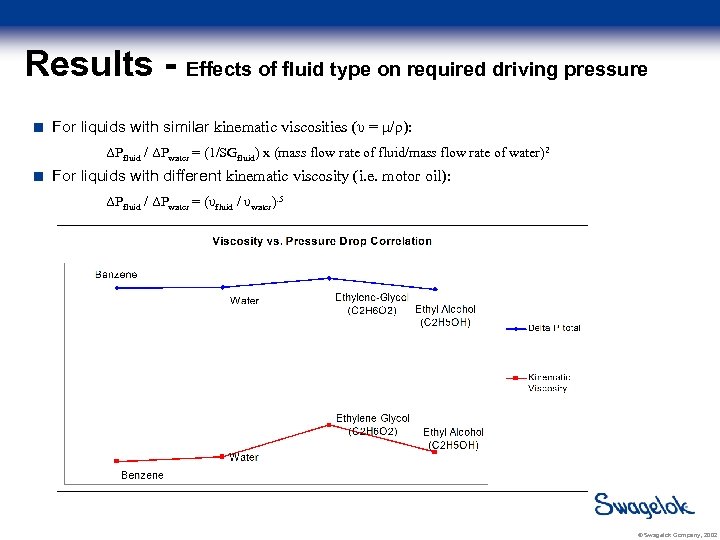 Results - Effects of fluid type on required driving pressure For liquids with similar kinematic viscosities (υ = μ/ρ): ΔPfluid / ΔPwater = (1/SGfluid) x (mass flow rate of fluid/mass flow rate of water)2 For liquids with different kinematic viscosity (i. e. motor oil): ΔPfluid / ΔPwater = (υfluid / υwater). 5 © Swagelok Company, 2002
Results - Effects of fluid type on required driving pressure For liquids with similar kinematic viscosities (υ = μ/ρ): ΔPfluid / ΔPwater = (1/SGfluid) x (mass flow rate of fluid/mass flow rate of water)2 For liquids with different kinematic viscosity (i. e. motor oil): ΔPfluid / ΔPwater = (υfluid / υwater). 5 © Swagelok Company, 2002
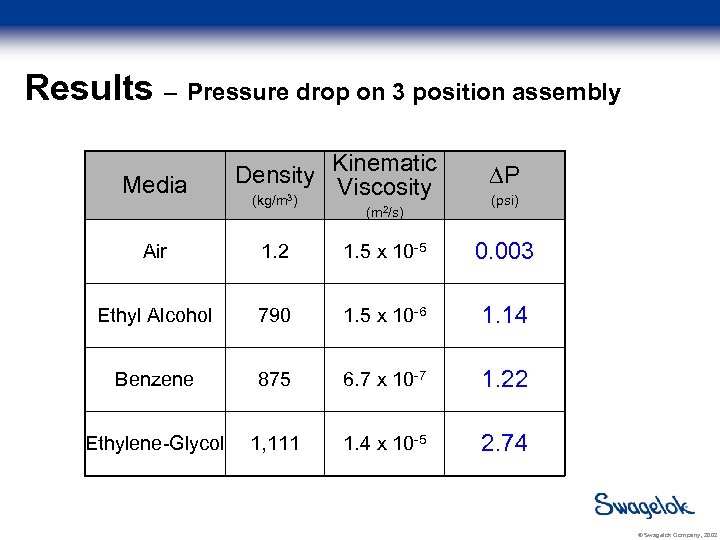 Results – Pressure drop on 3 position assembly Media Density (kg/m 3) Kinematic Viscosity (m 2/s) P (psi) Air 1. 2 1. 5 x 10 -5 0. 003 Ethyl Alcohol 790 1. 5 x 10 -6 1. 14 Benzene 875 6. 7 x 10 -7 1. 22 Ethylene-Glycol 1, 111 1. 4 x 10 -5 2. 74 © Swagelok Company, 2002
Results – Pressure drop on 3 position assembly Media Density (kg/m 3) Kinematic Viscosity (m 2/s) P (psi) Air 1. 2 1. 5 x 10 -5 0. 003 Ethyl Alcohol 790 1. 5 x 10 -6 1. 14 Benzene 875 6. 7 x 10 -7 1. 22 Ethylene-Glycol 1, 111 1. 4 x 10 -5 2. 74 © Swagelok Company, 2002
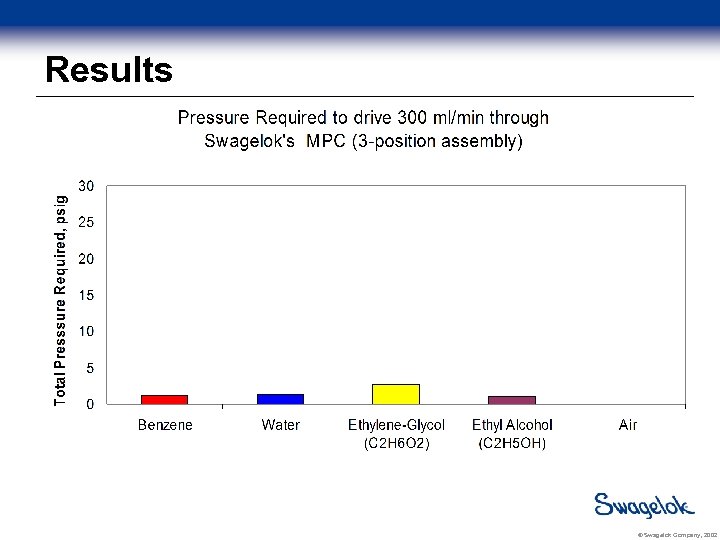 Results © Swagelok Company, 2002
Results © Swagelok Company, 2002
 Conclusions A valid model for predicting flow capacity of a Swagelok MPC system The surface-mount component has the largest effect on total system Cv Developed a valid equation for predicting pressure to drive liquids Based on kinematic viscosity MPC requires minimal driving pressure Visit Swagelok at Booth 51 © Swagelok Company, 2002
Conclusions A valid model for predicting flow capacity of a Swagelok MPC system The surface-mount component has the largest effect on total system Cv Developed a valid equation for predicting pressure to drive liquids Based on kinematic viscosity MPC requires minimal driving pressure Visit Swagelok at Booth 51 © Swagelok Company, 2002

