Computational Aerodynamics Using Unstructured Meshes Dimitri J Mavriplis

Computational Aerodynamics Using Unstructured Meshes Dimitri J. Mavriplis National Institute of Aerospace Hampton, VA 23666 National Institute of Aerospace March 21, 2003

Overview • Structured vs. Unstructured meshing approaches • Development of an efficient unstructured grid solver – Discretization – Multigrid solution – Parallelization • Examples of unstructured mesh CFD capabilities – Large scale high-lift case – Typical transonic design study • Areas of current research – Adaptive mesh refinement – Higher-order discretizations National Institute of Aerospace March 21, 2003

CFD Perspective on Meshing Technology • CFD Initiated in Structured Grid Context – Transfinite Interpolation – Elliptic Grid Generation – Hyperbolic Grid Generation • Smooth, Orthogonal Structured Grids • Relatively Simple Geometries National Institute of Aerospace March 21, 2003

CFD Perspective on Meshing Technology • Sophisticated Multiblock Structured Grid Techniques for Complex Geometries Engine Nacelle Multiblock Grid by commercial software True. Grid.

CFD Perspective on Meshing Technology • Sophisticated Overlapping Structured Grid Techniques for Complex Geometries Overlapping grid system on space shuttle (Slotnick, Kandula and Buning 1994)

Unstructured Grid Alternative • Connectivity stored explicitly • Single Homogeneous Data Structure National Institute of Aerospace March 21, 2003

Characteristics of Both Approaches • Structured Grids – – Logically rectangular Support dimensional splitting algorithms Banded matrices Blocked or overlapped for complex geometries • Unstructured grids – – – Lists of cell connectivity, graphs (edge, vertices) Alternate discretizations/solution strategies Sparse Matrices Complex Geometries, Adaptive Meshing More Efficient Parallelization National Institute of Aerospace March 21, 2003

Discretization • Governing Equations: Reynolds Averaged Navier. Stokes Equations – Conservation of Mass, Momentum and Energy – Single Equation turbulence model (Spalart-Allmaras) • Convection-Diffusion – Production • Vertex-Based Discretization – – 2 nd order upwind finite-volume scheme 6 variables per grid point Flow equations fully coupled (5 x 5) Turbulence equation uncoupled National Institute of Aerospace March 21, 2003

Spatial Discretization • Mixed Element Meshes – Tetrahedra, Prisms, Pyramids, Hexahedra • Control Volume Based on Median Duals – Fluxes based on edges – Single edge-based data-structure represents all element types National Institute of Aerospace March 21, 2003

Spatially Discretized Equations • Integrate to Steady-state • Explicit: – Simple, Slow: Local procedure • Implicit – Large Memory Requirements • Matrix Free Implicit: – Most effective with matrix preconditioner • Multigrid Methods National Institute of Aerospace March 21, 2003

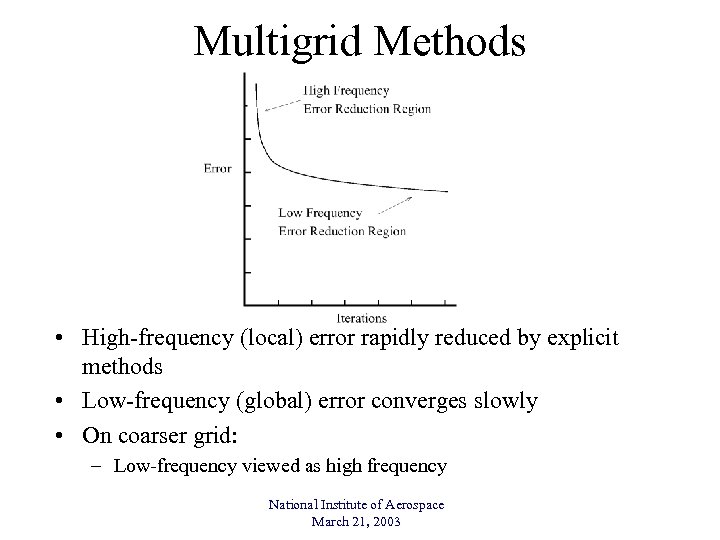Multigrid Methods • High-frequency (local) error rapidly reduced by explicit methods • Low-frequency (global) error converges slowly • On coarser grid: – Low-frequency viewed as high frequency National Institute of Aerospace March 21, 2003

Multigrid Correction Scheme (Linear Problems) National Institute of Aerospace March 21, 2003

Multigrid for Unstructured Meshes • • Generate fine and coarse meshes Interpolate between un-nested meshes Finest grid: 804, 000 points, 4. 5 M tetrahedra Four level Multigrid sequence

Geometric Multigrid • Order of magnitude increase in convergence • Convergence rate equivalent to structured grid schemes • Independent of grid size: O(N) National Institute of Aerospace March 21, 2003

Agglomeration vs. Geometric Multigrid • Multigrid methods: – Time step on coarse grids to accelerate solution on fine grid • Geometric multigrid – Coarse grid levels constructed manually – Cumbersome in production environment • Agglomeration Multigrid – Automate coarse level construction – Algebraic nature: summing fine grid equations – Graph based algorithm National Institute of Aerospace March 21, 2003

Agglomeration Multigrid • Agglomeration Multigrid solvers for unstructured meshes – Coarse level meshes constructed by agglomerating fine grid cells/equations National Institute of Aerospace March 21, 2003

Agglomeration Multigrid • Automated Graph-Based Coarsening Algorithm • Coarse Levels are Graphs • Coarse Level Operator by Galerkin Projection • Grid independent convergence rates (order of magnitude improvement)

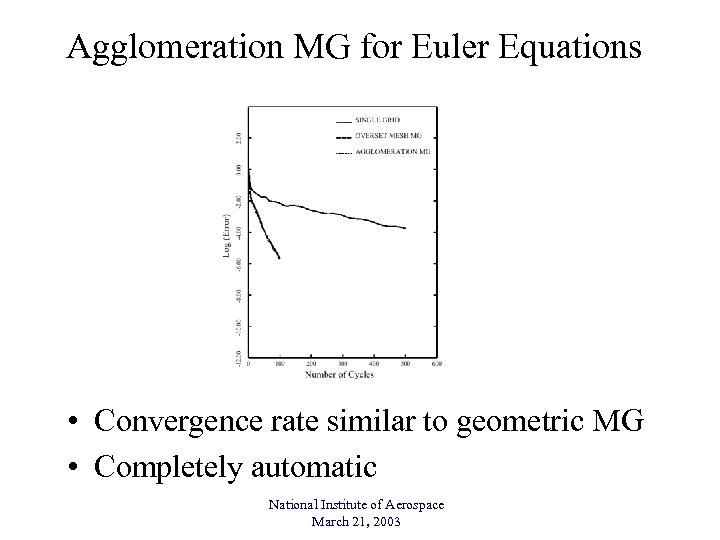Agglomeration MG for Euler Equations • Convergence rate similar to geometric MG • Completely automatic National Institute of Aerospace March 21, 2003

Anisotropy Induced Stiffness • Convergence rates for RANS (viscous) problems much slower then inviscid flows – Mainly due to grid stretching – Thin boundary and wake regions – Mixed element (prism-tet) grids • Use directional solver to relieve stiffness – Line solver in anisotropic regions National Institute of Aerospace March 21, 2003

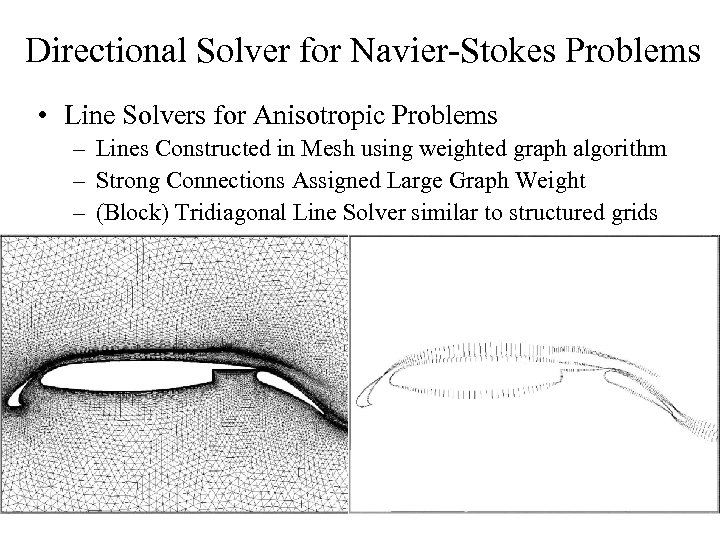Directional Solver for Navier-Stokes Problems • Line Solvers for Anisotropic Problems – Lines Constructed in Mesh using weighted graph algorithm – Strong Connections Assigned Large Graph Weight – (Block) Tridiagonal Line Solver similar to structured grids

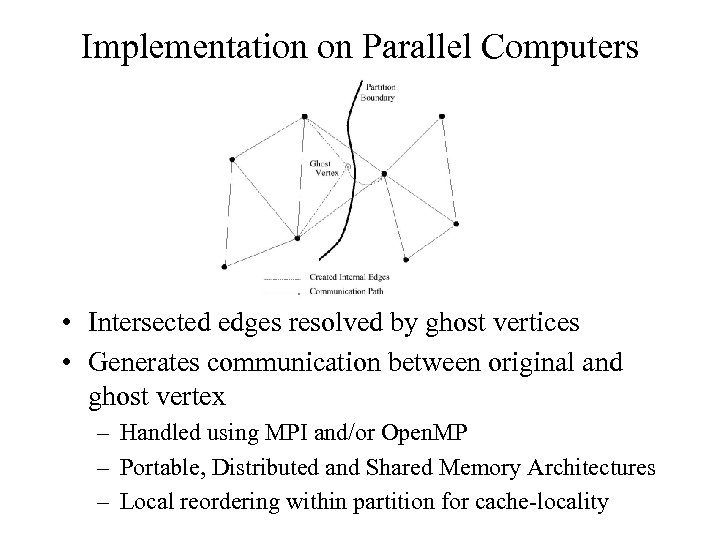Implementation on Parallel Computers • Intersected edges resolved by ghost vertices • Generates communication between original and ghost vertex – Handled using MPI and/or Open. MP – Portable, Distributed and Shared Memory Architectures – Local reordering within partition for cache-locality

Partitioning • Graph partitioning must minimize number of cut edges to minimize communication • Standard graph based partitioners: Metis, Chaco, Jostle – Require only weighted graph description of grid • Edges, vertices and weights taken as unity – Ideal for edge data-structure • Line solver inherently sequential – Partition around line using weighted graphs National Institute of Aerospace March 21, 2003

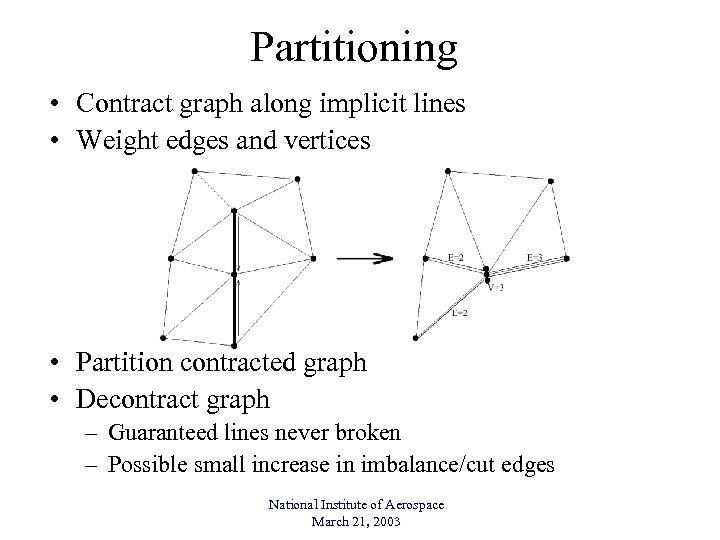Partitioning • Contract graph along implicit lines • Weight edges and vertices • Partition contracted graph • Decontract graph – Guaranteed lines never broken – Possible small increase in imbalance/cut edges National Institute of Aerospace March 21, 2003

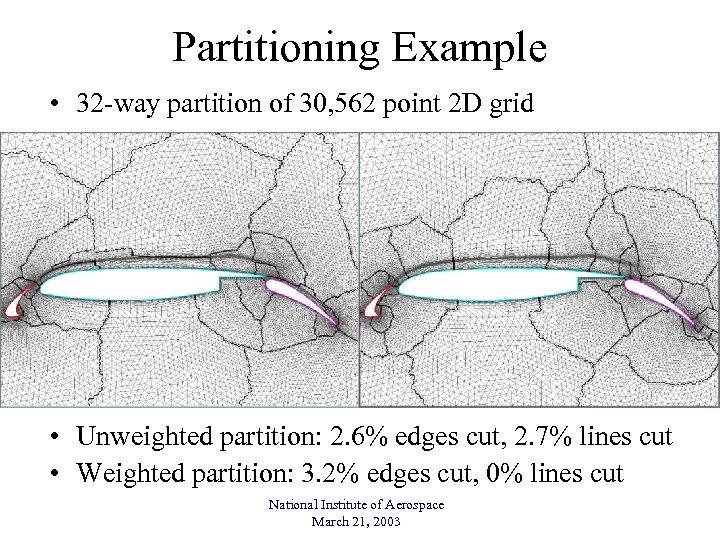Partitioning Example • 32 -way partition of 30, 562 point 2 D grid • Unweighted partition: 2. 6% edges cut, 2. 7% lines cut • Weighted partition: 3. 2% edges cut, 0% lines cut National Institute of Aerospace March 21, 2003

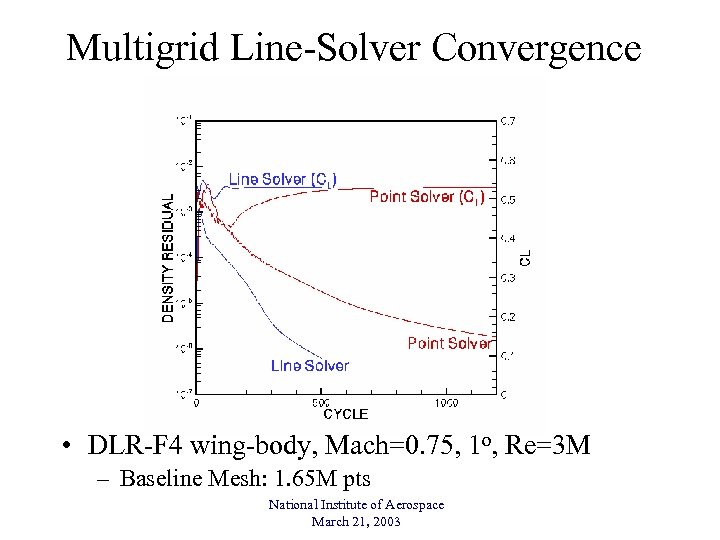Multigrid Line-Solver Convergence • DLR-F 4 wing-body, Mach=0. 75, 1 o, Re=3 M – Baseline Mesh: 1. 65 M pts National Institute of Aerospace March 21, 2003

Sample Calculations and Validation • Subsonic High-Lift Case – Geometrically Complex – Large Case: 25 million points, 1450 processors – Research environment demonstration case • Transonic Wing Body – Smaller grid sizes – Full matrix of Mach and CL conditions – Typical of production runs in design environment National Institute of Aerospace March 21, 2003

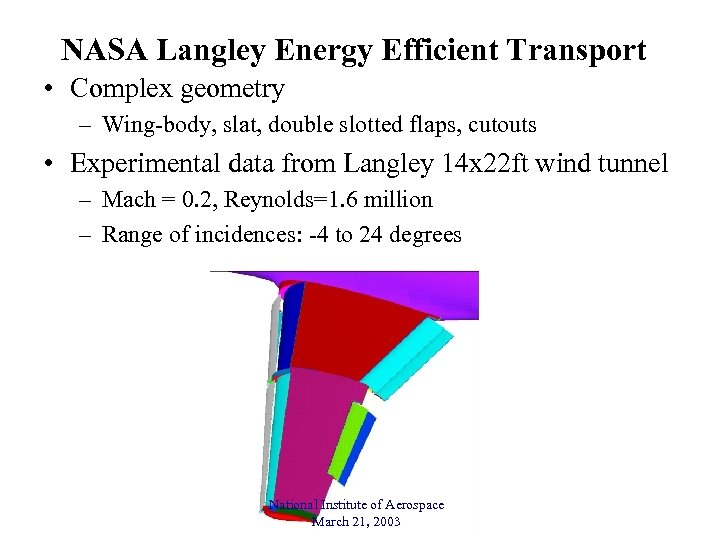NASA Langley Energy Efficient Transport • Complex geometry – Wing-body, slat, double slotted flaps, cutouts • Experimental data from Langley 14 x 22 ft wind tunnel – Mach = 0. 2, Reynolds=1. 6 million – Range of incidences: -4 to 24 degrees National Institute of Aerospace March 21, 2003

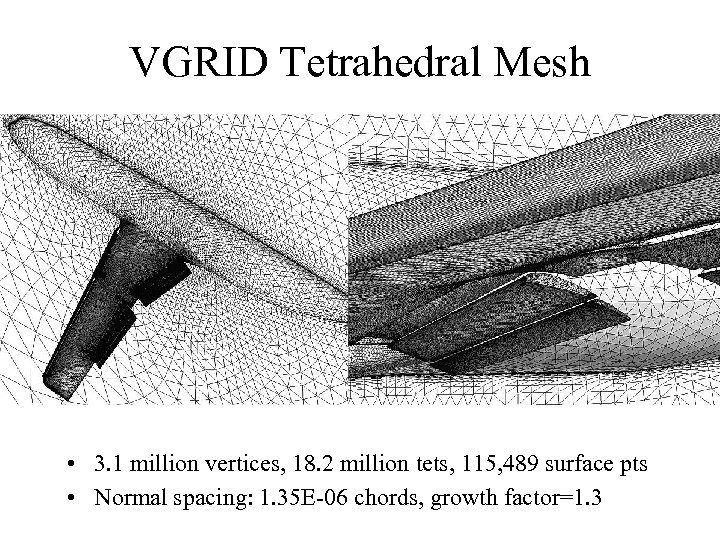VGRID Tetrahedral Mesh • 3. 1 million vertices, 18. 2 million tets, 115, 489 surface pts • Normal spacing: 1. 35 E-06 chords, growth factor=1. 3

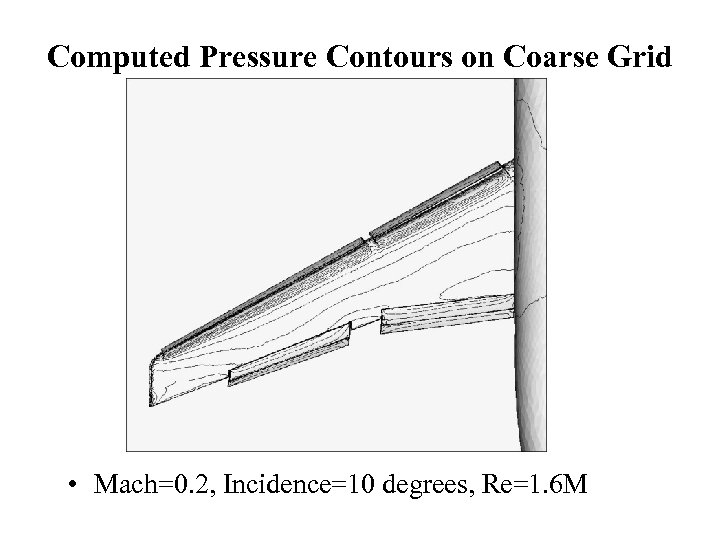Computed Pressure Contours on Coarse Grid • Mach=0. 2, Incidence=10 degrees, Re=1. 6 M

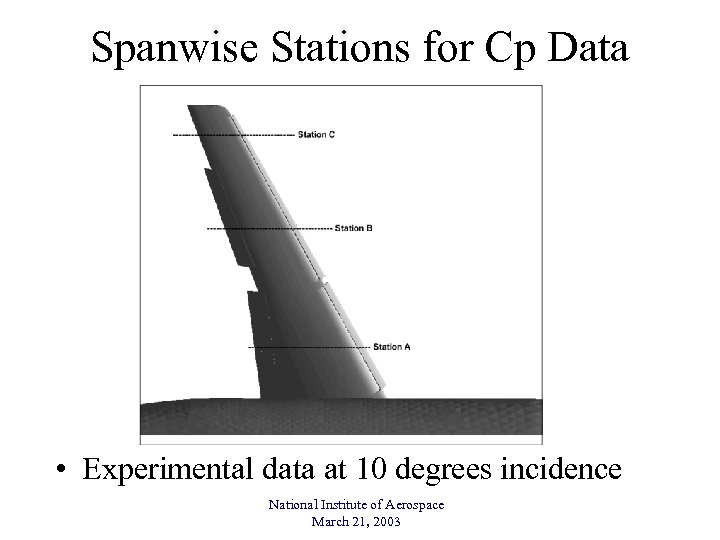Spanwise Stations for Cp Data • Experimental data at 10 degrees incidence National Institute of Aerospace March 21, 2003

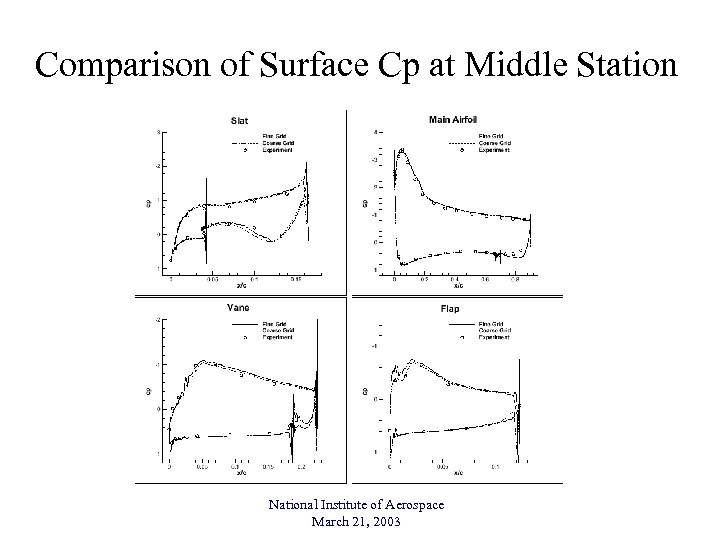Comparison of Surface Cp at Middle Station National Institute of Aerospace March 21, 2003

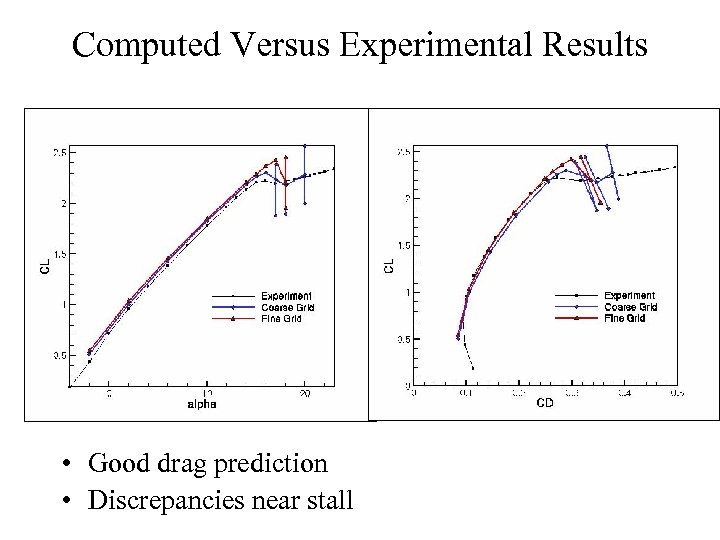Computed Versus Experimental Results • Good drag prediction • Discrepancies near stall

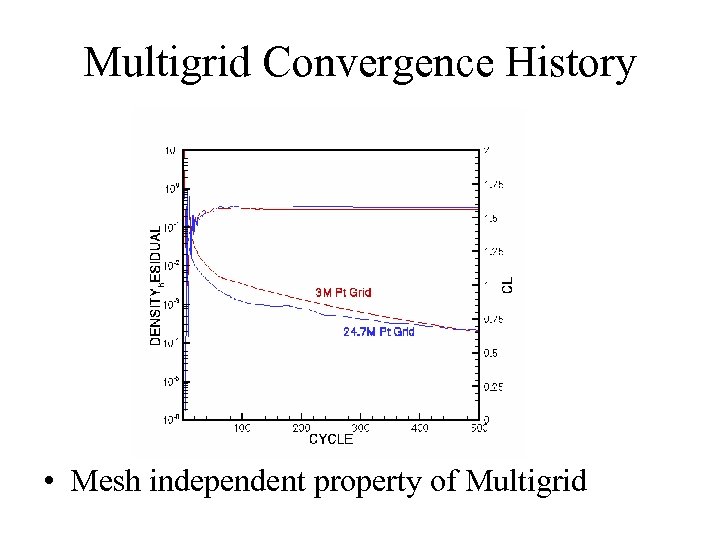Multigrid Convergence History • Mesh independent property of Multigrid

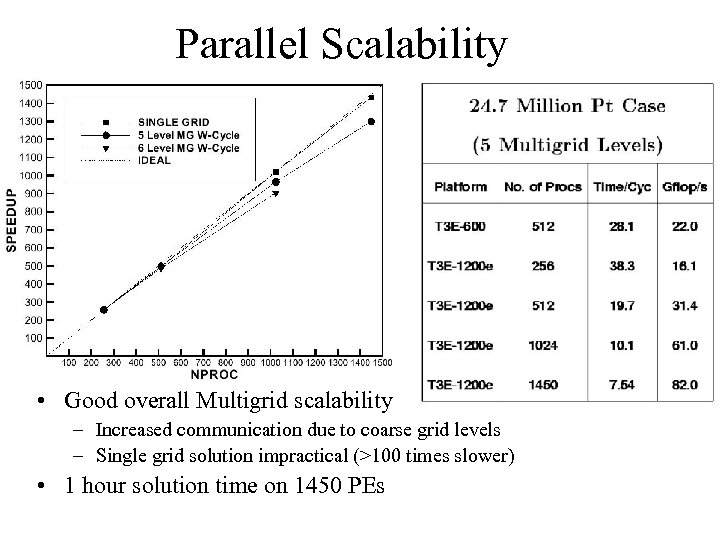Parallel Scalability • Good overall Multigrid scalability – Increased communication due to coarse grid levels – Single grid solution impractical (>100 times slower) • 1 hour solution time on 1450 PEs

AIAA Drag Prediction Workshop (2001) • Transonic wing-body configuration • Typical cases required for design study – Matrix of mach and CL values – Grid resolution study • Follow on with engine effects (2003)

Cases Run • Baseline grid: 1. 6 million points – Full drag Polars for Mach=0. 5, 0. 6, 0. 75, 0. 76, 0. 77, 0. 78, 0. 8 – Total = 72 cases • Medium grid: 3 million points – Full drag polar for each Mach number – Total = 48 cases • Fine grid: 13 million points – Drag polar at mach=0. 75 – Total = 7 cases National Institute of Aerospace March 21, 2003

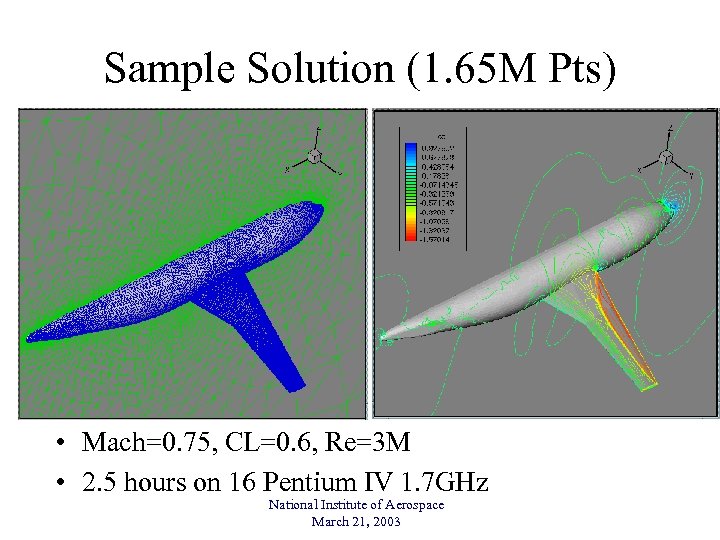Sample Solution (1. 65 M Pts) • Mach=0. 75, CL=0. 6, Re=3 M • 2. 5 hours on 16 Pentium IV 1. 7 GHz National Institute of Aerospace March 21, 2003

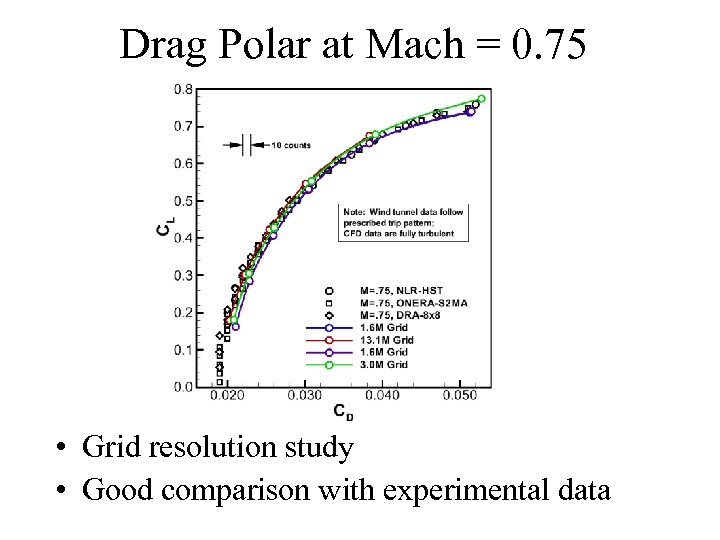Drag Polar at Mach = 0. 75 • Grid resolution study • Good comparison with experimental data

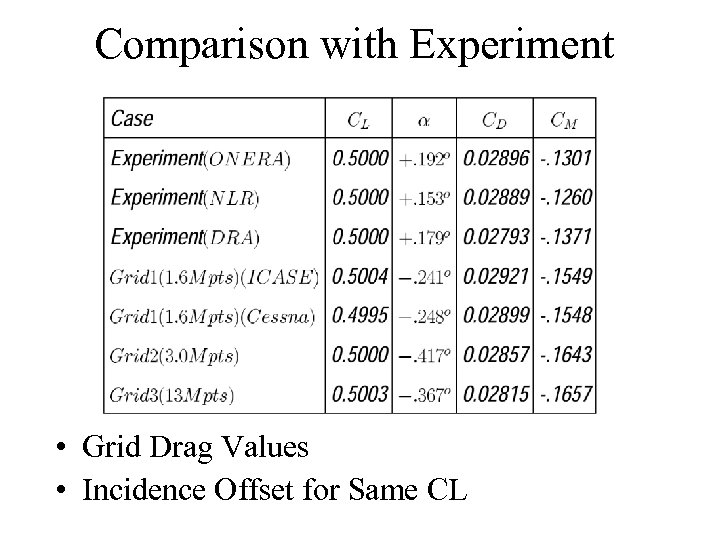Comparison with Experiment • Grid Drag Values • Incidence Offset for Same CL

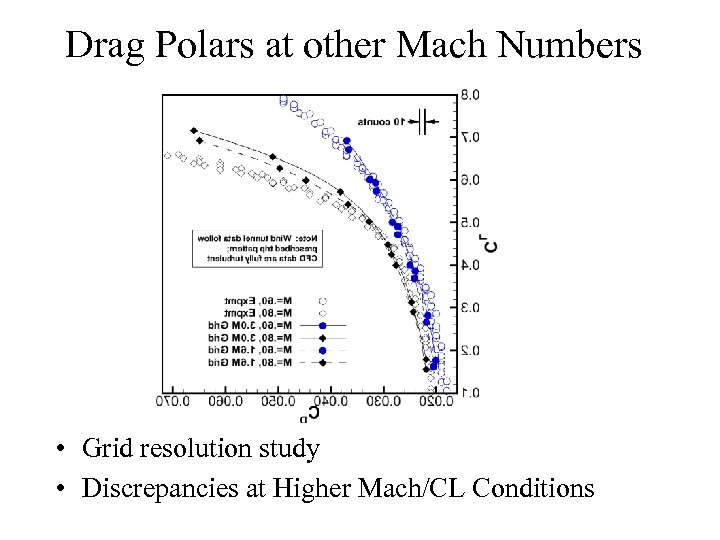Drag Polars at other Mach Numbers • Grid resolution study • Discrepancies at Higher Mach/CL Conditions

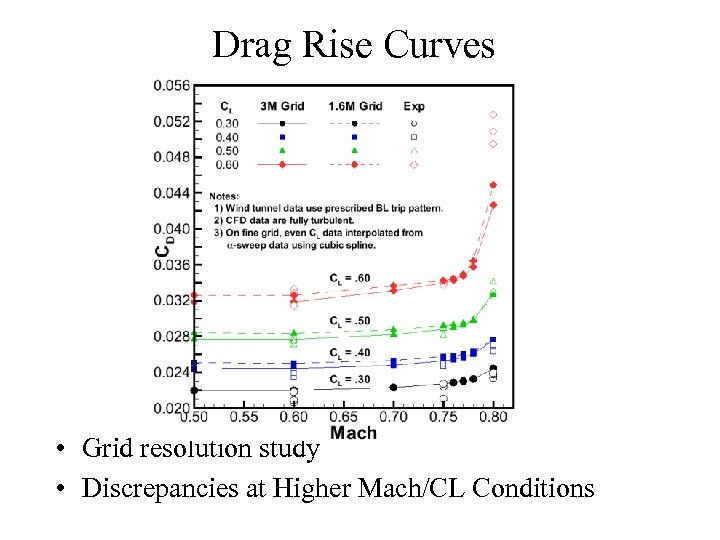Drag Rise Curves • Grid resolution study • Discrepancies at Higher Mach/CL Conditions

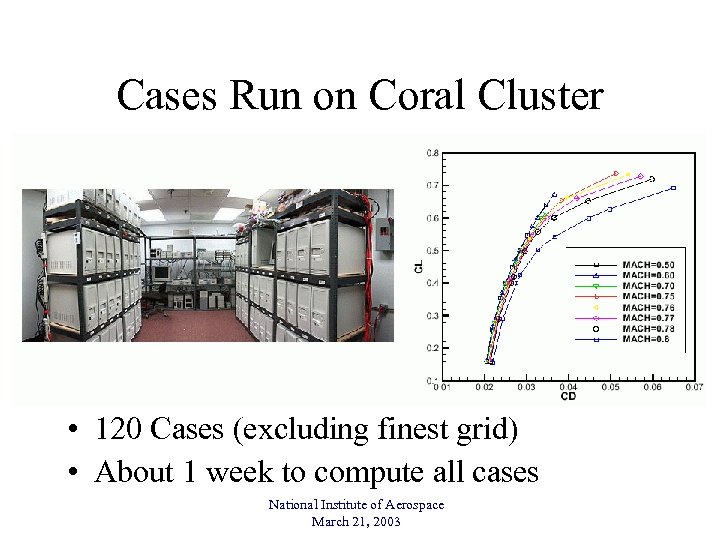Cases Run on Coral Cluster • 120 Cases (excluding finest grid) • About 1 week to compute all cases National Institute of Aerospace March 21, 2003

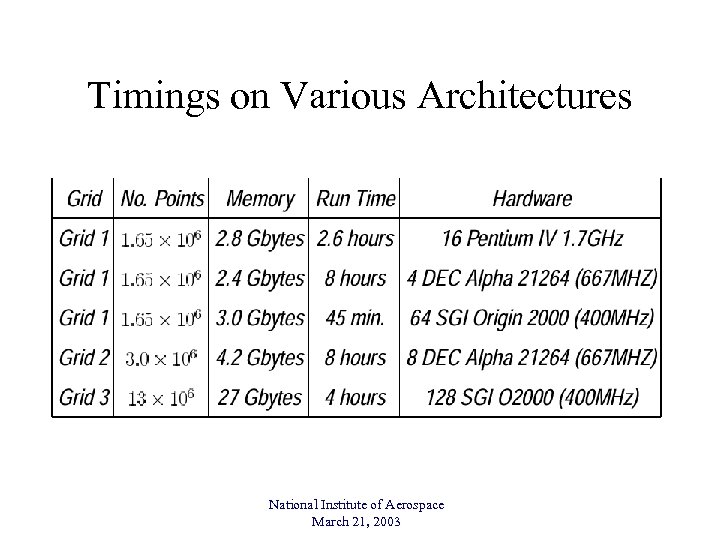Timings on Various Architectures National Institute of Aerospace March 21, 2003

Adaptive Meshing • Potential for large savings through optimized mesh resolution – Well suited for problems with large range of scales – Possibility of error estimation / control – Requires tight CAD coupling (surface pts) • Mechanics of mesh adaptation • Refinement criteria and error estimation National Institute of Aerospace March 21, 2003

Mechanics of Adaptive Meshing • Various well know isotropic mesh methods – Mesh movement • Spring analogy • Linear elasticity – – Local Remeshing Delaunay point insertion/Retriangulation Edge-face swapping Element subdivision • Mixed elements (non-simplicial) • Require anisotropic refinement in transition regions National Institute of Aerospace March 21, 2003

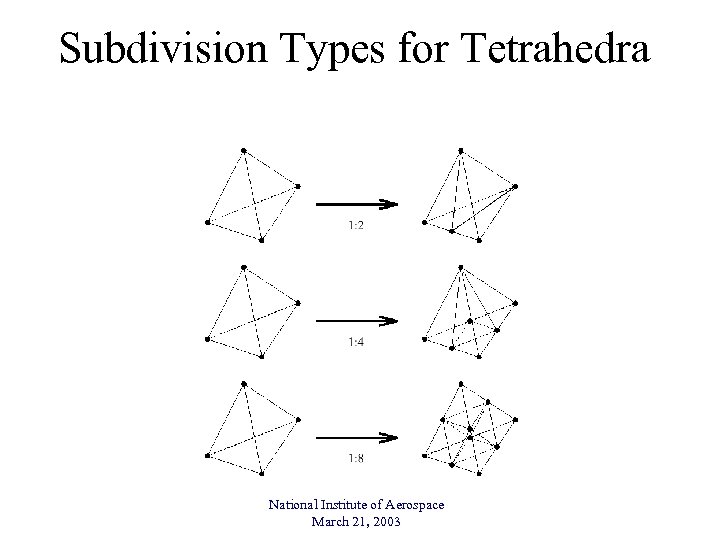Subdivision Types for Tetrahedra National Institute of Aerospace March 21, 2003

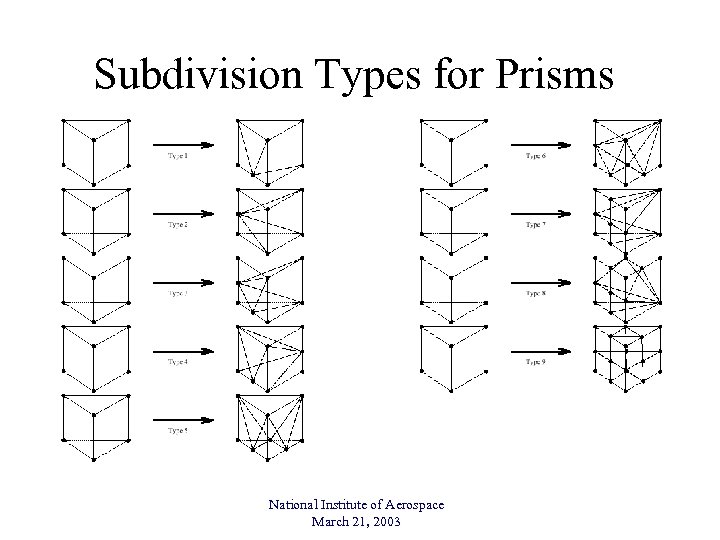Subdivision Types for Prisms National Institute of Aerospace March 21, 2003

Subdivision Types for Pyramids National Institute of Aerospace March 21, 2003

Subdivision Types for Hexahedra National Institute of Aerospace March 21, 2003

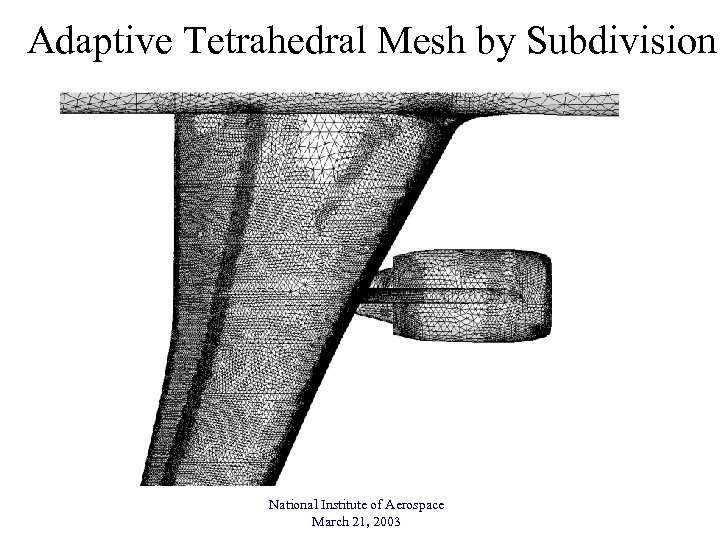Adaptive Tetrahedral Mesh by Subdivision National Institute of Aerospace March 21, 2003

Adaptive Hexahedral Mesh by Subdivision National Institute of Aerospace March 21, 2003

Adaptive Hybrid Mesh by Subdivision National Institute of Aerospace March 21, 2003

High-Order Accurate Discretizations • Uniform X 2 refinement of 3 D mesh: – Work increase = factor of 8 – 2 nd order accurate method: accuracy increase = 4 – 4 th order accurate method: accuracy increase = 16 • For smooth solutions • Potential for large efficiency gains – Spectral element methods – Discontinuous Galerkin (DG) – Streamwise Upwind Petrov Galerkin (SUPG) National Institute of Aerospace March 21, 2003

Higher-Order Methods • Most effective when high accuracy required • Potential role in aerodynamics (drag prediction) – High accuracy requirements – Large grid sizes required

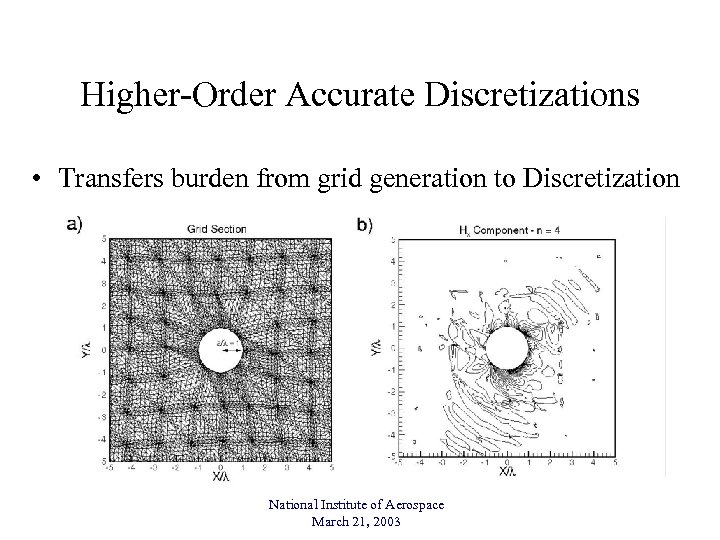Higher-Order Accurate Discretizations • Transfers burden from grid generation to Discretization National Institute of Aerospace March 21, 2003

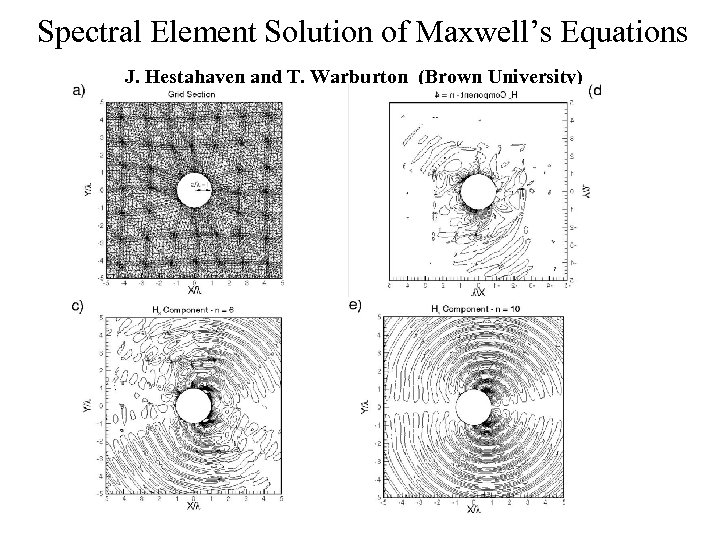Spectral Element Solution of Maxwell’s Equations J. Hestahaven and T. Warburton (Brown University)

Combined H-P Refinement • Adaptive meshing (h-ref) yields constant factor improvement – After error equidistribution, no further benefit • Order refinement (p-ref) yields asymptotic improvement – Only for smooth functions – Ineffective for inadequate h-resolution of feature – Cannot treat shocks • H-P refinement optimal (exponential convergence) – Requires accurate CAD surface representation National Institute of Aerospace March 21, 2003

Conclusions • Unstructured mesh technology enabling technology for computational aerodynamics – Complex geometry handling facilitated – Efficient steady-state solvers – Highly effective parallelization • Accurate solutions possible for on-design conditions – Mostly attached flow – Grid resolution always an issue • Orders of Magnitude Improvement Possible in Future – Adaptive meshing – Higher-Order Discretizations • Future work to include more physics – Turbulence, transition, unsteady flows, moving meshes