Compositional Verification for System-on-Chip Designs SRC Student Symposium

Compositional Verification for System-on-Chip Designs SRC Student Symposium Paper 16. 5 Nishant Sinha Edmund Clarke Carnegie Mellon University

Overview • Compositional Reasoning • Verifying HDL challenges • Synchronous Intermediate Language (SIL) • Automated Compositional Reasoning for SIL • An example • Making it efficient

Compositional Reasoning • Verification of a concurrent hardware/software system by direct composition does not scale – State space explosion • Compositional Reasoning is a divide-and-conquer approach to alleviate the state space explosion

HDL Verification • Hardware Description Languages (HDLs) – Verilog, System. C, System. Verilog – Basis of industrial So. C design • Towards formal verification – Problems: informally specified semantics, language peculiarities – Need standard formal semantics • Although informal semantics differ, several notions/operators are common – Synchronous execution via delta-cycles, blocking/non-blocking assignments • We define a synchronous intermediate language (SIL) with common HDL operators and constructs

Synchronous Intermediate Lang. (SIL) • A SIL Program consists of one or more modules – Modules execute synchronously – Communicate by global shared variables • Each module specified in an imperative style – Initialization and Combinational Logic blocks • Variable Types: bit-vectors, integers • Guarded control flow • Blocking (Immediate)/ Non-blocking (Delayed) assignments

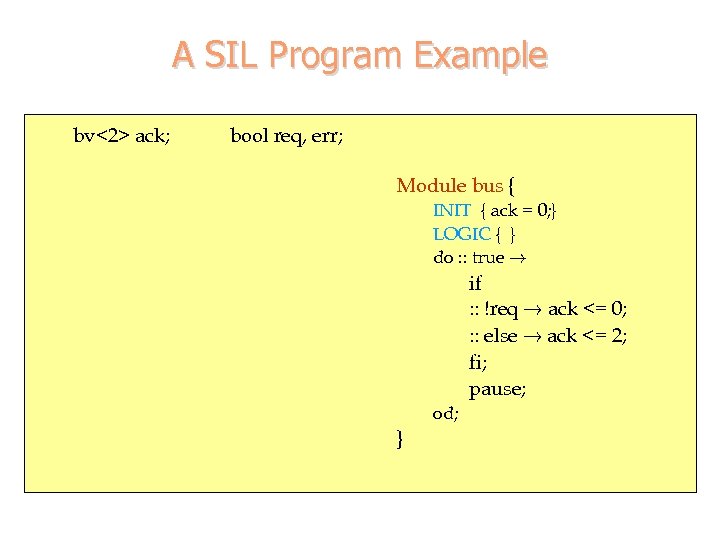A SIL Program Example bv<2> ack; bool req, err; Module bus { INIT { ack = 0; } LOGIC { } do : : true ! if : : !req ! ack <= 0; : : else ! ack <= 2; fi; pause; od; }

SIL Safety Property Checking

Automated Compositional Reasoning • Assume-Guarantee Reasoning (AGR) – M 1, M 2 are Kripke structures, P is a CFA • Automatically generate assumption CFA A – Based on work by Cobleigh et al. ’ 03 • Use learning algorithm for regular languages, L* – L* is assisted by a model checker

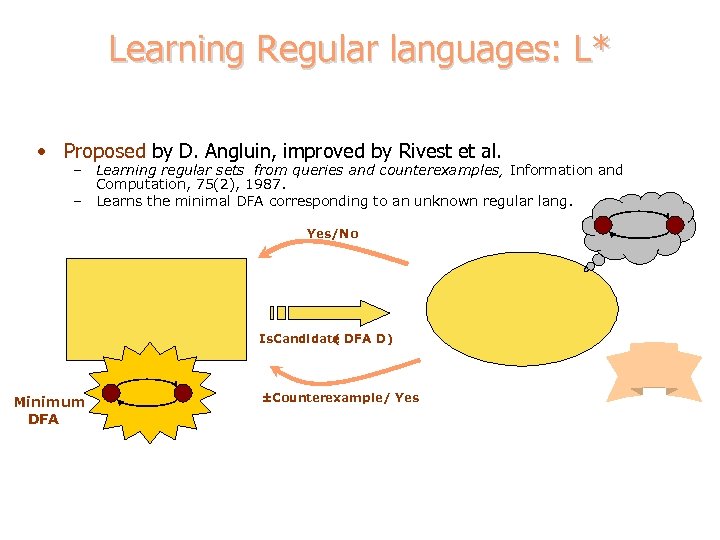Learning Regular languages: L* • Proposed by D. Angluin, improved by Rivest et al. – Learning regular sets from queries and counterexamples, Information and Computation, 75(2), 1987. – Learns the minimal DFA corresponding to an unknown regular lang. Yes/No Is. Candidate DFA D ) ( Minimum DFA ±Counterexample/ Yes

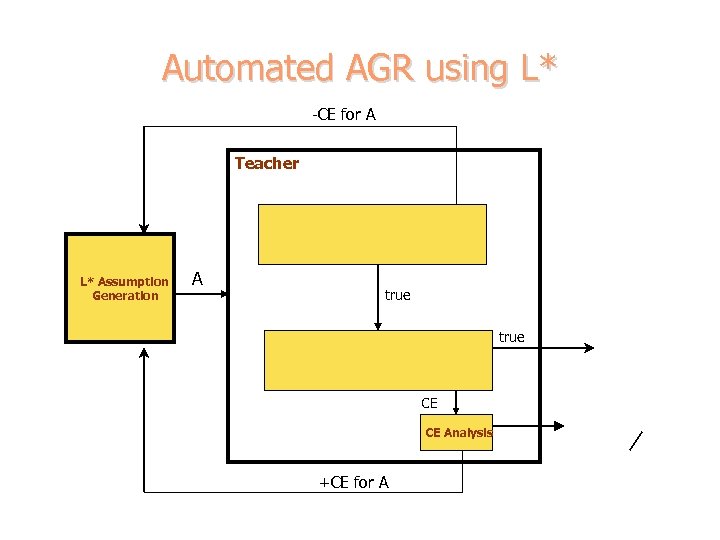Automated AGR using L* -CE for A Teacher L* Assumption Generation A true CE CE Analysis +CE for A

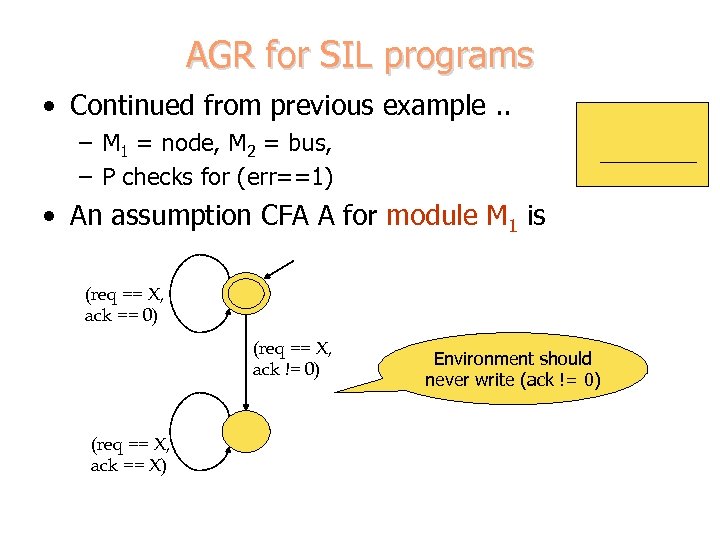AGR for SIL programs • Continued from previous example. . – M 1 = node, M 2 = bus, – P checks for (err==1) • An assumption CFA A for module M 1 is (req == X, ack == 0) (req == X, ack != 0) (req == X, ack == X) Environment should never write (ack != 0)

Making it efficient • Two main problems: – Each module itself has a huge state space • Idea: Use Bounded model checker as a teacher • Fast membership query replies – Naïve learning suffers from alphabet explosion • Idea: Cluster alphabet during learning • Fewer membership queries • Ongoing implementation in SYMODA – SYnchronous MODular Analyzer

Related Work • RTL Verilog program verification – Via Predicate abstraction • Andraus et al. , Jain et al. – Via Symbolic Simulation • Kolbl et al. • Via Translations to SMV-like languages – Verilog: VIS, Brayton et al. – System. C: Moy et al. , Tahar et al. • None of these approaches are compositional

Related Work • Compositional Hardware Verification – – Mcmillan ’ 99 (using SMV) Khashidashvili et al. ’ 06 (net-list level) Chen et al. ’ 06 (using Murphi) … • None of the above approaches are automated