Complexity Theory Lecture 10 Lecturer Moni Naor

Complexity Theory Lecture 10 Lecturer: Moni Naor

Recap Last week: IP=PSPACE Start with #P in PSPACE Public vs. Private Coins IP[k]=AM Mechanism for showing non NP-Completeness This Week: Statistical zero-knowledge AM protocol for VC dimension Hardness and Randomness

Lack of certificate Bug or feature? Disadvantages clear, but: • Advantage: proof remains `property’ of prover and not automatically shared with verifier • Very important in cryptographic applications – Zero-knowledge Honest verifier perfect zero-knowledge • Many variants • Can be used to transform any protocol designed to work with benign players into one working with malicious ones – The computational variant is useful for this purpose • Can be used to obtain (plausible) deniability

Perfect or Statistical Zero-Knowledge An interactive protocol for proving that x 2 L is honest verifier perfect zero-knowledgeif for all x 2 L: there exists a probabilistic polynomial time simulator S such that S(x) generates an output identically distributedto the verifier’s view in a real execution: – transcript of (P, V) conversation – the random bits used by the verifier • assume no erasures, otherwise can get it trivially If the distributions are nearly identical – Statistical Zero-Knowledge Variation distance is negligible in program size Example: the protocol for GNI is honest verifier perfect zero-knowledge. The transcript consist of a graph H graph and a bit r The simulator: given (G 0, G 1) Pick random c 2 R {0, 1} and 2 R S|V| Output simulated view: transcript h. H = (Gc), r=ci random string: hc, i The distribution is identical to the one generated by an honest verifier Some precautions need to be taken if the verifier might not be following the protocol

Detour: Authentication One of the fundamental tasks of cryptography • Alice (sender) wants to send a message m to Bob (receiver). • They want to prevent Eve from interfering – Bob should be sure that the message he receives is indeed the message m Alice sent. Alice Bob Eve

Authentication and Non-Repudiation • Key idea of modern cryptography [Diffie-Hellman]: can make authentication (signatures) transferable to third party - Non-repudiation. – Essential to contract signing, e-commerce… • Digital Signatures: last 25 years major effort in – Research • Notions of security • Computationally efficient constructions – Technology, Infrastructure (PKI), Commerce, Legal

Is non-repudiation always desirable? Not necessarily so: • Privacy of conversation, no (verifiable) record. – Do you want everything you ever said to be held against you? • If Bob pays for the authentication, shouldn't be able to transfer it for free • Perhaps can gain efficiency

Deniable Authentication Setting: • Sender has a public key known to receiver • Want to come up with an (perhaps interactive) authentication scheme such that the receiver keeps no receipt of conversation. This means: • Any receiver could have generated the conversation itself. – There is a simulator that for any message m and verifier V* generates an indistinguishableconversation. – Similar to Zero-Knowledge! – An example where zero-knowledge is the ends, not the means! Proof of security consists of Unforgeability and Deniability

Ring Signatures and Authentication Can we keep the sender anonymous? Idea: prove that the signer is a member of an ad hoc set – Other members do not cooperate – Use their `regular’ public-keys • Encryption – Should be indistinguishablewhich member of the set is actually doing the authentication Bob Alice? Eve

Deniable Ring Authentication Completeness: a good sender and receiver complete the authentication on any message m Unforgeability. Existential unforgeable against adaptive chosen message attack for any sequence of messages m 1, m 2, … mk Adversarially chosen in an adaptive manner Even if sender authenticates all of m 1, m 2, … mk Probability forger convinces receiver to accept a m { m 1, m 2, … mk } is negligible Properties of an interactive authentication scheme

Deniable Ring Authentication Deniability – For any verifier, for any arbitrary set of keys, some good some bad, there is simulator that can generate computationally indistinguishable conversations. • A more stringent requirement: statisticallyindistinguishable Source Hiding: – For any verifier, for any arbitrary set of keys, some good some bad, the source is computationally indistinguishableamong the good keys • A more stringent requirement: statisticallyindistinguishable Source Hiding and Deniability – incomparable

Encryption • Assume a public key encryption scheme E Plaintext – Public key PK – knowing PK can encrypt message m • generate Y=E(PK , m, r) Ciphertext – With corresponding secret key PS, given Y can retrieve m • m =D(PS , Y) • Encryption process is probabilistic Each message induces a distribution on the ciphertexts • Security of encryption scheme: – non-malleable against chosen ciphertext attacks in the post-processing mode. – In particular given Y=E(PK, m, r) hard to generate Y’=E(PK, m’, r’) for a related message m’ • Example of a very malleable scheme: one-time pad

A Public Key Authentication Protocol P has a public key PK of an encryption scheme E. To authenticate a message m: • V P : Choose x R {0, 1}n. Send Y=E(PK, m°x , r) • P V : Verify that prefix of plaintext is indeed m. If yes - send x. V accepts if the received x’=x Is it Unforgeable? Is it Deniable?

Security of the scheme Unforgeability: depends on the strength of E • Sensitive to malleability: – if given E(PK, m°x, r) can generate E(PK, m’°x’, r) where m’ is related to m and x’ is related to x then can forge. • The protocol allows a chosen ciphertext attack on E. – Even of the post-processing kind! • Can prove that any strategy for existential forgery can be translated into a CCA strategy on E • Works even against concurrent executions. Deniability: does V retain a receipt? ? – It does not retain one for an honest V – Need to prove knowledge of x

Simulator for honest receiver Choose x R {0, 1}n. Output: h. Y=E(PK, m°x, r), x, ri Has exactly the same distribution as a real conversation when the verifier is following the protocol Statistical indistinguishability Verifier might cheat by checking whether certain ciphertext have as a prefix m No known concrete way of doing harm this way

Encryption: Implementation • Under any trapdoor permutation - rather inefficient [DDN]. • Cramer & Shoup: Under the Decisional DH assumption – Requires a few exponentiations. • With Random Oracles: several proposals – RSA with OAEP - same complexity as vanilla RSA [Crypto’ 2001] – Can use low exponent RSA/Rabin • With additional Interaction: J. Katz’s non malleable POKS?

Encryption as Commitment When the public key PK is fixed and known Y=E(PK, x, r) can be seen as commitmentto x To open x reveal r, the random bits used to create Y Perfect binding: from unique decryption For any Y there are no two different x and x’ and r’ s. t. Y=E(PK, x, r) =E(PK, x’, r’) Secrecy: no information about x is leaked to those not knowing private key PS

Deniable Protocol P has a public key K of an encryption scheme E. To authenticate message m: • V P: Choose x r{0, 1}n. Send Y=E(PK, m°x , r) • P V: Send E(PK, x, t) • V P: Send x and r - opening Y=E(PK, m°x, r) • P V: Open E(PK, x , t) by sending t.

Security of the scheme Unforgeability: as before - depends on the strength of E can simulate previous scheme (with access to D(PK , . )) Important property: E(PK, x, t) is a non-malleable commitment (wrt the encryption) to x. Deniability: can run simulator: • Extract x by running with E(PK, garbage, t) and rewinding • Expected polynomial time • Need the semantic securityof E - it acts as a commitment scheme

Ring Signatures and Authentication Want to keep the sender anonymous by proving that the signer is a member of an ad hoc set – Other members do not cooperate – Use their `regular’ public-keys – Should be indistinguishable which member of the set is actually doing the authentication Bob Alice? Eve

Ring Authentication Setting • A ring is an arbitrary set of participants including the authenticator • Each member i of the ring has a public encryption key PKi – Only i knows the corresponding secret key PSi • To run a ring authentication protocol both sides need to know PK 1, PK 2, …, PKn the public keys of the ring members . . .

An almost Good Ring Authentication Protocol Ring has public keys PK 1, PK 2, …, PKn of encryption scheme E To authenticate message m with jth decryption key PSj: V P: Choose x {0, 1}n. Send E(PK 1, m°x, r 1), E(PK 2, m°x, r 2), …, E(PKn, m°x, rn) P V: Decrypt E(PKj, m°x, rj), using PSj and Send E(PK 1, x, t 1), E(PK 2, x, t 2), …, E(PKn, x, tn) V P: open all the E(PKi, m°x, ri) by Send x and r 1, r 2 , … rn P V: Verify consistency and open all E(PKi, x, ti) by Send t 1, t 2 , … tn Problem: what if not all suffixes(x‘s) are equal

The Ring Authentication Protocol Ring has public keys PK 1, PK 2, …, PKn of encryption scheme E To authenticate message m with jth decryption key PSj: V P: Choose x {0, 1}n. Send E(PK 1, m°x, r 1), E(PK 2, m°x, r 2), …, E(PK 1, m°x, rn) P V: Decrypt E(PKj, m°x, rj), using PSj and Send E(PK 1, x 1, t 1), E(PK 2, x 2, t 2), …, E(PKn, xn, tn) Where x=x 1+x 2 + xn V P: open all the E(PKi, m°x, ri) by Send x and r 1, r 2 , … rn P V: Verify consistency and open all E(PKi, x, ti) by Send t 1, t 2 , … tn and x 1, x 2 , …, xn

Complexity of the scheme Sender: single decryption, n encryptions and n encryption verifications Receiver: n encryptions and n encryption verifications Communication Complexity: O(n) public-key encryptions

Security of the scheme Unforgeability: as before (assuming all keys are well chosen) since E(PK 1, x 1, t 1), E(PK 2, x 2, t 2), …, E(PK 1, xn, tn) where x=x 1+x 2 + xn is a non-malleable commitment to x Source Hiding: which key was used (among well chosen keys) is – Computationally indistinguishable during protocol – Statistically indistinguishable after protocol • If ends successfully Deniability: Can run simulator `as before’

Promise Problems A promise problem L is similar to a language recognition problem except that there is a set A • if x 2 A then should report correctly whether x 2 L or not • if x 2 A then do not care how algorithm responds Example: unique sat A={ |either is not statisfiable or has a unique satisfying assumption} O satisfying assignments 1 satisfying assignment If A={0, 1}n, then this is the usual language recognition problem

Statistical Zero-Knowledge So if statistical zero-knowledge is so good, why not use it all the time? Definition: L is a promise problem SZK={L|L has a statistical zero-knowledge protocol} HVSZK={L|L has an honest verifier statistical zeroknowledge protocol} Clearly: SZK µ HVSZK since any protocol good against all verifiers is good against honest ones as well

The surprising world of Statistical Zero-Knowledge • There are complete problems for HVSZK – Entropy Difference (ED): given two circuits generating distributions D 1 and D 2 distinguish between the cases H(D 1) ¸ H(D 2)+1 and H(D 2) ¸ H(D 1)+1 H(D)= x Pr. D[x] log Pr. D[x] Any promise problem in HVSZK problem is Karp reducible to ED – ED has an honest verifier public-coins statistical zero-knowledge protocol in constant number of rounds – VD( , ) is also complete • Conclusions: – All languages and promise problems in HVSZK have public coins protocols – HVSZK is closed under complementation • If a promise problem L has a public coins statistical zero-knowledge proof system then it has one with good against general verifier • Conclusions: – SZK is closed under complementation – SZK 2 AM Å Co-AM

Homework • Show an AM protocol for Entropy Difference when the two distribution are promised also to be flat – For x and x’ such that Pr[x] ≠ 0 and Pr[x’] ≠ 0 we have Pr[x] = Pr[x’] Is the protocol SZK or HVSZK?

Statistical Zero-Knowledge Theorem: if a language L has a statistical zero-knowledge proof system, then L 2 AM Å Co-AM Conclusion: if interested in zero-knowledge proofs for all languages in NP need to either – Relax notion of proof: argument • Prover is assumed to be a polynomial time machine This led to PCP – Having access to some secret information • Such protocols exists assuming a certain kind of commitment exists – Based on one-way permutations • Another possible relaxation of proof: assume that there are two provers who do not exchange information during the execution of the protocol – Relax notion of zero-knowledge: computational • There exists a simulator which generates computationally indistinguishable distributions • Such protocols exists for all of IP assuming one-way function exist

Sources for Statistical Zero-Knowledge • Salil Vadhan Thesis: www. eecs. harvard. edu/~salil/papers/phdthesis-abs. html • Results are due to Goldreich, Sahai and Vadhan • Building on – Fortnow and Aiello and Hastad: SZK µ AM Å Co-AM – Okamoto: SZK is closed under complementation

VC Dimension Let T=(U, S) be a set system – Each s 2 S is a subset of ground set U We say that X µ U is shattered by T if 8 X’ µ X there is an s 2 S is such that X’=s Å X The VC-Dimension of T [Vapnik Chervonenkis]: the maximum cardinality of any set X shattered by a T The complexity of determining the VC-Dimension of T=(U, S): If (U, S) is given explicitly then since VC(U, S) · log |S| , Can determine in |U| log |S| time Known to be at as hard as solving sat with log 2 n variables If (U, S) is given implicitly by a circuit C. , For j 2 U and 1 · i · |S| the value C(i, j)=1 iff j 2 si and 0 otherwise The problem of determining VC(C) is complete for 3 P Will see that showing an approximate lower bound on VC is in AM

AM Protocol for 2 -approximating the VC Dimension Conditions for large VC-dimension Sauer’s Lemma: in any set T=(U, S) such that i=0 m (|U|i ) · |S| we have that m+1 · VC(U, S). Large collections have a lower bound on the VC dimension Lemma is also due to Perles and Shelah Idea for protocol: Merlin gives the set X that is shattered by the set system encoded in circuit C. If X is `mostly’ shattered, For more than half of X’ µ X there is an s 2 S is such that X’=s Å X then there must be a large Y µ X that is fully shattered: Consider T’=(X, S’) where each s’ 2 S’ is equal to s Å X for some s 2 S If |S’| is large - at least ½ 2|X| ¸ i=0|X|/2 (|X|i ) after removing duplicates, then Sauer’s Lemma implies that VC(T’) ¸ |X|/2

The protocol Input: circuit C encoding set system (U, S) and promise that Either VC(U, S)¸ k 1. • 2. • Arthur should always accept if Merlin follows the protocol or VC(U, S)· k/2 Arthur should reject with reasonable probability The protocol: We know that VC(U, S) · log |S| Merlin: send set X µ U that is shattered by the set system encoded in C. Arthur: Pick a random X’ µ X and send it Merlin: send index 1 · i · |S| such that X’ = si Å X where si={j|C(i, j)=1} Arthur: verify that X’ = si Å X by running C on all j 2 X

Open Problems • Many problems can be formulated as – For a fixed huge graph • E. g. nodes correspond to permutations – Given two nodes, what is the length of the shortest path between them • Is it possible to apply the AM approach to show that various problems of finding distances in huge graphs are not NP-Hard. – Either exact version or approximate Examples: • Pancake Problem – Given n pancakes of various sizes in an arbitrary order what is the minimum number of flips to sort them Genome Rearrangement problems: • Sorting by transpositions • Sorting by translocation

Idea for protocol Verifier • Pick at random one of the two nodes as a starting point • Make a random work of certain length and give prover end point Prover: • Determine the which node is the starting point

References • See Tzvika Hartman’s Ph. D thesis (Weizmann Institute) The diameter of the Pancake Graph Program – Bill Gates and Christos Papadimitriou: Bounds For Sorting By Prefix Reversal. Discrete Mathematics, vol 27, pp. 47 -57, 1979. – H. Heydari and H. I. Sudborough: On the Diameter of the Pancake Network. Journal of Algorithms, 1997

What’s next Natural development of Interactive Proofs: • PCP: Probabilistically Checkable Proofs – The prover sends the a polynomial sized proof – The verifier checks only small parts of it A new characterization of NP Can reduce any problem • Main applications: – – Inapproximability of many optimization problems Low communication cryptographic protocols Get back to it towards end of course

Derandomization A major research question: • How to make the construction of – Small Sample space `resembling’ large one – Hitting sets Efficient. Successful approach: randomness from hardness – (Cryptographic) pseudo-random generators – Complexity oriented pseudo-random generators

Recall: Derandomization I Collection that should resemble probability of success on ALL inputs Bad Good 1 - Chernoff Theorem: any f 2 BPP has a polynomial size circuit Simulating large sample spaces • Want to find a small collection of strings on which the PTM behaves as on the large collection – If the PTM errs with probability at most , then should err on at most + of the small collection • Choose m random strings • For input x event Ax is more than ( + ) of the m strings fail the PTM -2 2 m < 2 -2 n Pr[Ax] · e Pr[[x Ax] · x Pr[Ax] < 2 n 2 -2 n=1

Pseudo-random generators • Would like to stretch a short secret (seed) into a long one • The resulting long string should be usable in any case where a long string is needed – In particular: cryptographic application as a one-time pad • Important notion: Indistinguishability Two probability distributions that cannot be distinguished – Statistical indistinguishability: distances between probability distributions – New notion: computational indistinguishability

Computational Indistinguishability Definition: two sequences of distributions {Dn} and {D’n} on {0, 1}n are computationally indistinguishable if for every polynomial p(n) for every probabilistic polynomial time adversary A for sufficiently large n If A receives input y {0, 1}n and tries to decide whether y was generated by Dn or D’n then |Prob[A=‘ 0’ | Dn ] - Prob[A=‘ 0’ | D’n ] | < 1/p(n) Without restriction on probabilistic polynomial tests: equivalent to variation distancebeing negligible ∑β {0, 1}n |Prob[ Dn = β] - Prob[ D’n = β]| < 1/p(n) advantage

Pseudo-random generators Definition: a function g: {0, 1}* → {0, 1}* is said to be a (cryptographic) pseudo-random generator if • It is polynomial time computable • It stretches the input |g(x)|>|x| – denote by ℓ(n) the length of the output on inputs of length n • If the input (seed) is random, then the output is indistinguishable from random For any probabilistic polynomial time adversary A that receives input y of length ℓ(n) and tries to decide whether y= g(x) or is a random string from {0, 1}ℓ(n) for any polynomial p(n) and sufficiently large n |Prob[A=`rand’| y=g(x)] - Prob[A=`rand’| y R {0, 1}ℓ(n)] | < 1/p(n) Want to use the output a pseudo-random generator whenever long random strings are used Anyone who considers arithmetical methods of producing random numbers is, of course, in a state of sin. J. von Neumann

Pseudo-random generators Definition: a function g: {0, 1}* → {0, 1}* is said to be a (cryptographic) pseudo-random generator if • It is polynomial time computable • It stretches the input g(x)|>|x| – denote by ℓ(n) the length of the output on inputs of length n • If the input is random the output is indistinguishable from random For any probabilistic polynomial time adversary A that receives input y of length ℓ(n) and tries to decide whether y= g(x) or is a random string from {0, 1}ℓ(n) for any polynomial p(n) and sufficiently large n |Prob[A=`rand’| y=g(x)] - Prob[A=`rand’| y R {0, 1}ℓ(n)] | < 1/p(n) Important issues: • Why is the adversary bounded by polynomial time? • Why is the indistinguishability not perfect?

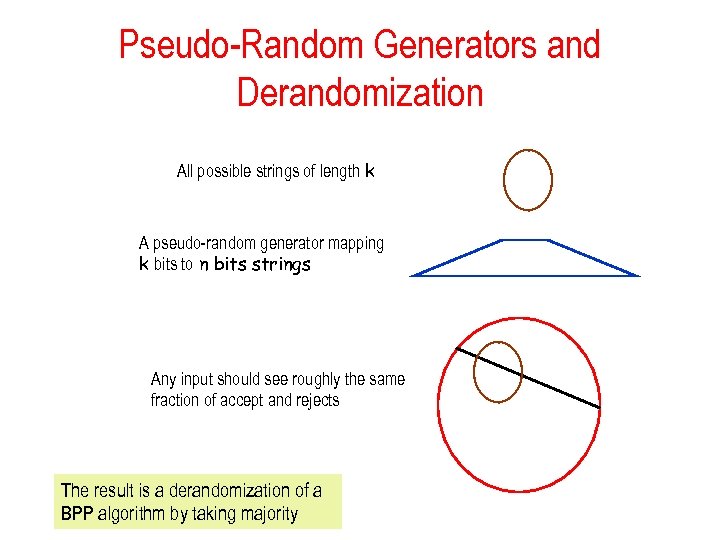Pseudo-Random Generators and Derandomization All possible strings of length k A pseudo-random generator mapping k bits to n bits strings Any input should see roughly the same fraction of accept and rejects The result is a derandomization of a BPP algorithm by taking majority

Complexity of Derandomization • Need to go over all 2 k possible input string • Need to compute the pseudo-random generator on those points • The generator has to be secure against non-uniform distinguishers: – The actual distinguisher is the combinationof the algorithm and the input • If we want it to work for all inputs we get the non-uniformity

Construction of pseudo-random generators randomness from hardness • Idea: for any given a one-way function there must be a hard decision problem hidden there • If balanced enough: looks random • Such a problem is a hardcore predicate • Possibilities: – Last bit – First bit – Inner product

Hardcore Predicate Definition: let f: {0, 1}* → {0, 1}* be a function. We say that h: {0, 1}* → {0, 1} is a hardcore predicate for f if • It is polynomial time computable • For any probabilistic polynomial time adversary A that receives input y=f(x) and tries to compute h(x) for any polynomial p(n) and sufficiently large n |Prob[A(y)=h(x)] - 1/2| < 1/p(n) where the probability is over the choice y and the random coins of A • Sources of hardcoreness: – not enough information about x • not of interest for generating pseudo-randomness – enough information about x but hard to compute it

Single bit expansion • Let f: {0, 1}n → {0, 1}n be a one-way permutation • Let h: {0, 1}n → {0, 1} be a hardcore predicate for f Consider g: {0, 1}n → {0, 1}n+1 where g(x)=(f(x), h(x)) Claim: g is a pseudo-random generator Proof: can use a distinguisher for g to guess h(x) f(x), h(x)) f(x), 1 -h(x))

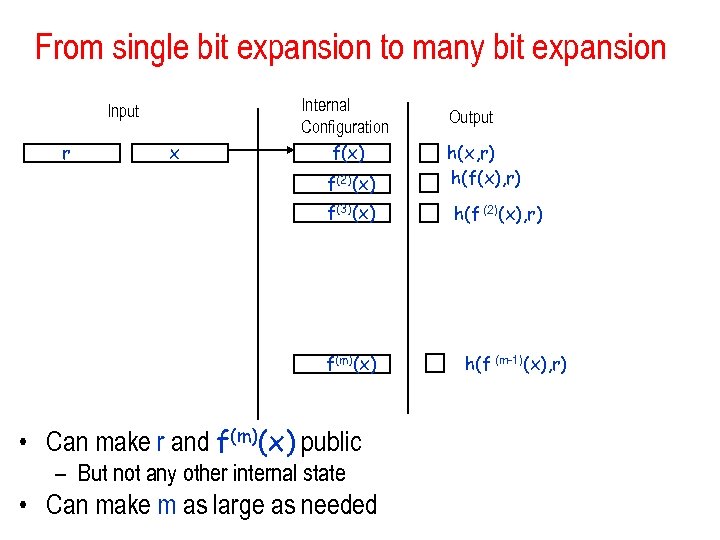From single bit expansion to many bit expansion Input r x Internal Configuration f(x) f(2)(x) f(3)(x) f(m)(x) • Can make r and f(m)(x) public – But not any other internal state • Can make m as large as needed Output h(x, r) h(f(x), r) h(f (2)(x), r) h(f (m-1)(x), r)

Two important techniques for showing pseudo-randomness • Hybrid argument • Next-bit prediction and pseudo-randomness

Hybrid argument To prove that two distributions D and D’ are indistinguishable: • suggest a collection of distributions D= D 0, D , … Dk =D’ 1 such that If D and D’ can be distinguished, there is a pair Di and Di+1 that can be distinguished. Advantage ε in distinguishing between D and D’ means advantage ε/k between some Di and Di+1 Use such a distinguisher to derive a contradiction

Next-bit Test Definition: a function g: {0, 1}* → {0, 1}* is said to pass the next bit test if • It is polynomial time computable • It stretches the input |g(x)|>|x| – denote by ℓ(n) the length of the output on inputs of length n • If the input (seed) is random, then the output passes the next-bit test For any prefix 0≤ i< ℓ(n), for any probabilistic polynomial time adversary A that receives the first i bits of y= g(x) and tries to guess the next bit, or any polynomial p(n) and sufficiently large n |Prob[A(yi, y 2, …, yi) = yi+1] – 1/2 | < 1/p(n) Theorem: a function g: {0, 1}* → {0, 1}* passes the next bit test if and only if it is a pseudo-random generator

Complexity Oriented Pseudo-Random Generators Cryptography Derandomization • Only crude upper bound on • when derandomizing an the time of the `user’ algorithm you have a much better idea about the – Distinguisher resources – In particular know the run time • The generator has more • The generator has less computational power than – May be from a higher the distinguisher complexity class Quantifier order switch

Ideas for getting better pseudo-random generators for derandomization • The generator need not be so efficient • For derandomizing – a parallel algorithm generator may be more sequential • Example: to derandomize AC 0 circuits can compute parities – A low memory algorithm may use more space In particular we can depart from the one-way function assumption • Easy one-way hard the other • The (in)distinguishing probability need not be so small – We are going to take a majority at the end

Parameters of a complexity oriented pseudo-random generator All functions of n • • • Seed length t Output length m Running time nc fooling circuits of size s error ε Any circuit family {Cn} of size s(n) that tries to distinguish outputs of the generator from random strings in {0, 1}m(n) has at most ε(n) advantage

Hardness Assumption: Unapproximable Functions Definition: E = [k DTIME(2 kn) Average hardness Definition: A family of functions f = {fn} notion fn: {0, 1}n {0, 1} is said to be s(n)-unapproximableif for every family of circuits {Cn} of size s(n): Prx[Cn(x) = fn(x)] ≤ ½ + 1/s(n) is both the circuit size and the bound on the advantage Example: if g is a one-way permutation and h is a hardcore function strong against s(n)- adversaries, then f(y)=h(g-1(y)) is s(n)-unapproximable

One bit expansion Assumption: f = {fn } is – s(n)-unapproximable, for s(n) = 2Ω(n) – in E Claim: G = {Gn}: Gn(y) = y◦flog n(y) is a single bit expansion generator family Parameters seed length t = log n output length m=log n + 1 fooling circuits of size s nδ running time nc error ε = δ < 1/m 1/n Proof: suppose not, then • There exists a predictor that computes flog n with probability better than ½ + 1/s(log n) on a random input • As in the single bit expansion using hardcore functions

Getting Many Bits Simultaneously Try outputting many evaluations of f on various parts of the seed: Let bi(y) be a projection of y and consider G(y) = f(b 1(y))◦f(b 2(y))◦…◦f(bm(y)) • Seems that a predictor must evaluate f(bi(y)) to predict ith bit • But: predictor might use correlationswithout having to compute f • Turns out: sufficient to decorrelate the bi(y)’s in a pairwise manner If |y|=t and S µ {1. . . t} we denote by y|S the sequence of bits of y whose index is in S

Nearly-Disjoint Subsets Definition: a collection of subsets S 1, S 2, …, Sm {1…t} is an (h, a)-design if: – Fixed size: for all i, |Si| = h – Small intersection for all i ≠ j, |Si Å Sj| ≤ a : {1. . . t} S 2 Each of size h S 1 Each intersection of size · a S 3 Parameters: (m, t, h, a)

Nearly-Disjoint Subsets Lemma: for every ε > 0 and m < n can construct in poly(n) time a collection of subsets S 1, S 2, …, Sm {1…t} which is a (h, a)-design with the following parameters: • h = log n, • a = εlog n design • t is O(log n). Both a proof of existence and a sequential construction

Nearly-Disjoint Subsets Proof: construction in a greedy manner repeat m times: – pick a random (h=log n)-subset of {1…t} – set t = O(log n) so that: • expected overlap with a fixed Si is ½εlog n • probability overlap with Si is larger than εlog n is at most 1/m – Can get by picking a single element independently from t’ buckets of size ½ ε For Si event Ai is: intersection is larger than (1/2 + )t’ 2 Pr[Ai] · e-2 t’ < 2 -log m – Union bound: some h-subset has the desired small overlap with all the Si picked so far – find the good h-subset by exhaustive search

Other construction of designs • Based on error correcting codes • Simple construction: based on polynomials

The NW generator Nisan-Wigderson Need: • f E that is s(n)-unapproximable, for s(n) = 2δn • A collection S 1, …, Sm {1…t} which is an (h, a) design with h=log n, a = δlog n/3 and t = O(log n) Gn(y)=flog n(y|S 1)◦flog n(y|S 2)◦…◦flog n(y|Sm) flog n: 010100101111101010111001010 A subset Si seed y

The NW generator Theorem: G={Gn} is a complexity oriented pseudo-random generator with: – – – seed length t = O(log n) output length m = nδ/3 running time nc for some constant c fooling circuits of size s = m error ε = 1/m

The NW generator • Proof: – assume G={Gn} does not -pass a statistical test C = {Cm} of size s: |Prx[C(x) = 1] – Pry[C( Gn(y) ) = 1]| > ε – can transform this distinguisherinto a predictor A of size s’ = s + O(m): Pry[A(Gn(y)1…i-1) = Gn(y)i] > ½ + ε/m • just as in the next-bit test using a hybrid argument

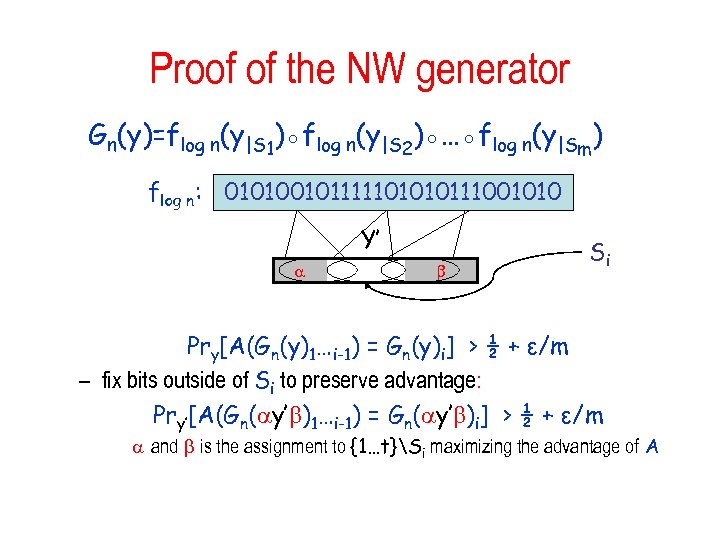Proof of the NW generator Gn(y)=flog n(y|S 1)◦flog n(y|S 2)◦…◦flog n(y|Sm) flog n: 010100101111101010111001010 Y’ Si Pry[A(Gn(y)1…i-1) = Gn(y)i] > ½ + ε/m – fix bits outside of Si to preserve advantage: Pry’[A(Gn( y’ )1…i-1) = Gn( y’ )i] > ½ + ε/m and is the assignment to {1…t}Si maximizing the advantage of A

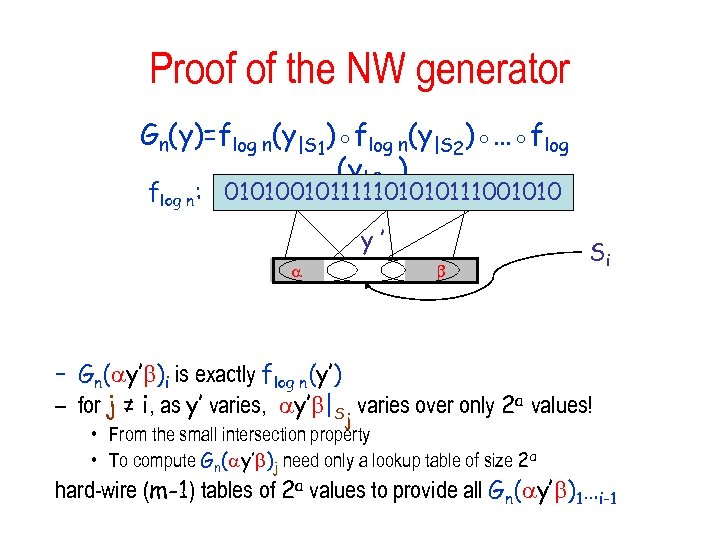Proof of the NW generator Gn(y)=flog n(y|S 1)◦flog n(y|S 2)◦…◦flog n(y|Sm) flog n: 010100101111101010111001010 y’ Si – Gn( y’ )i is exactly flog n(y’) – for j ≠ i, as y’ varies, y’ |Sj varies over only 2 a values! • From the small intersection property • To compute Gn( y’ )j need only a lookup table of size 2 a hard-wire (m-1) tables of 2 a values to provide all Gn( y’ )1…i-1

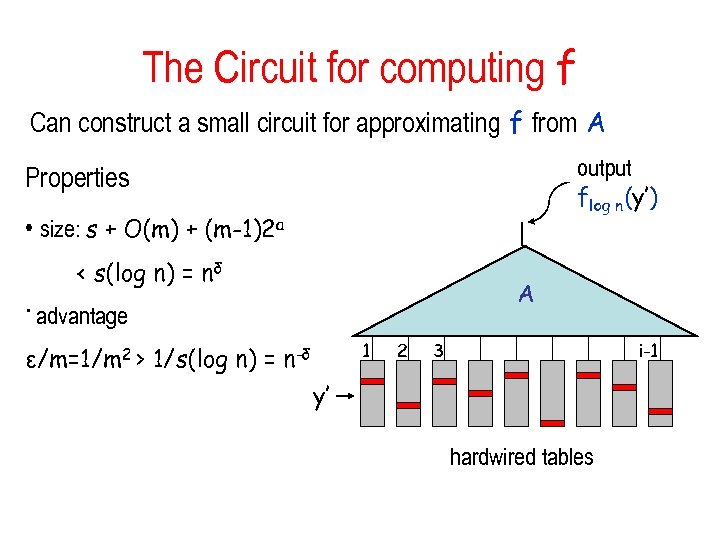The Circuit for computing f Can construct a small circuit for approximating f from A output flog n(y’) Properties • size: s + O(m) + (m-1)2 a < s(log n) = nδ A • advantage 1 ε/m=1/m 2 > 1/s(log n) = n-δ 2 3 i-1 y’ hardwired tables

References • Theory of cryptographic Pseudo-randomness developed by: – Blum and Micali, next bit test, 1982 – Computational indistinguishability, Yao, 1982, • The NW generator: – Nisan and Wigderson, Hardness vs. Randomness, JCSS, 1994. – Some of the slides on the topic: Chris Umans’ course Lecture 9