Complex Numbers nth roots using De Moivre s Theorem

Complex Numbers nth roots using De Moivre’s Theorem

Objectives • To find the cube roots of unity using De Moivre’s Theorem • To find the nth roots of any complex number using De Moivre’s Theorem

Cube roots of unity • We have already found the cube roots of unity algebraically by solving z 3 – 1 =0. • We also saw that the sum of the three cube roots of unity was zero and that each complex root is the square of the other complex root. • We will now use De Moivre’s Theorem to find the cube roots of unity.

Cube roots of unity • Let cosθ + isinθ be one of the cube roots so: (This implies that the modulus, r, is 1) • Using De Moivre’s Theorem we can therefore say:

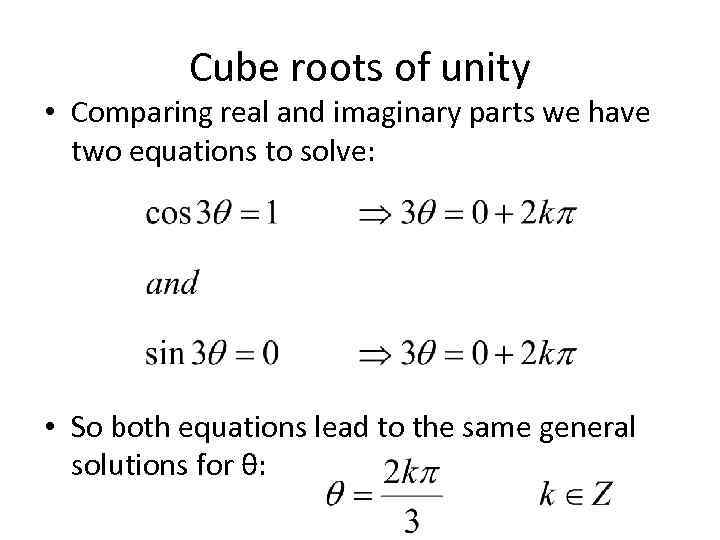
Cube roots of unity • Comparing real and imaginary parts we have two equations to solve: • So both equations lead to the same general solutions for θ:

Cube roots of unity • Choosing values of k to obtain all solutions in the range – π < θ ≤ π:

Cube roots of unity • So using these arguments (θ) and the modulus r = 1 we find the three cube roots of unity in polar form are:

Cube roots of unity • This agrees with the properties previously found: – that the sum of the roots equals zero – that the vectors on an Argand diagram are each separated by equal angles of 2π/3 and lie on a circle or radius 1 – that each complex number is equal to the square of the other • On this last point, we can observe that if this is true then |z 22|=|z 3| and arg(z 22) = arg(z 3) and vice versa.

Cube roots of unity • To show that |z 22|=|z 3| and arg(z 22) = arg(z 3) are true and vice versa then we should remember the product rules: – |z 2| = |zz| = |z||z| – arg(z 2) = arg(zz) = arg(z) + arg(z) = 2 arg(z) • So, – |z 22|=|z 2 z 2|=|z 2|= 1 x 1 =|z 3| – arg(z 22) = arg(z 2 z 2) = arg(z 2) + arg(z 2) = 2 x 2π/3 = 4π/3 = – 2π/3 = arg(z 3)

Cube roots of unity • We can still use the Greek letter omega, ω, to denote one of the complex roots, i. e. : – the three cube roots of unity are 1, ω and ω2 – 1 + ω2 = 0 – and ω3 = 1

nth roots of unity (where n is a positive integer) • If we consider the above method but let cosθ + isinθ be one of the nth roots of unity we can say that: (Again this implies that the modulus, r, is 1) • And therefore using De Moivre’s Theorem:

nth roots of unity • Comparing real and imaginary parts we have two equations to solve: • So both equations lead to the same general solutions for θ:

nth roots of unity • Taking k = 1, 2, …, n will obtain all distinct values of θ, and therefore cosθ + isinθ, in the range 0 < θ ≤ 2π. • Therefore there are n distinct nth roots of unity. The general nth root is given by (remembering that the modulus is 1):

nth roots of unity • The nth roots of unity are:

nth roots of unity • The nth roots of unity have the properties: – the sum of the roots equals zero – the vectors on an Argand diagram are each separated by equal angles of 2π/n and lie on a circle or radius 1 – one of the roots has a principal argument of zero, i. e. one root is 1 • We will now consider what happens when we square the first root with a positive, non-zero argument.

nth roots of unity (refer to diagram on p 302 of yellow Bostock, Chandler & Rourke book) • Now the first positive, non-zero argument will occur when k = 1, i. e. arg(z 1) = 2π/n • Remember that: arg(zk) = 2 kπ/n • And that: arg(z 2) = 2 arg(z) • So, arg(z 12) = 2 x 2π/n = 4π/n = arg(z 2) • The modulus for all roots is 1.

nth roots of unity • This means that considering the complex roots z 1 and z 2 we conclude that: z 12 = z 2 • Now consider cubing z 1 and remember that: arg(z 3) = 3 arg(z) • So, arg(z 13) = 3 x 2π/n = 6π/n = arg(z 3) • Hence, z 13 = z 3

nth roots of unity • Continuing this pattern gives: z 1 2 = z 2 z 1 3 = z 3 … z 1 r = z r … z 1 n = z n = 1

nth roots of unity • So if omega, ω, denotes the complex number with the first positive, non-zero argument then the nth roots of unity are: ω = z 1 ω 2 = z 1 2 = z 2 ω 3 = z 1 3 = z 3 … ω r = z 1 r = z r … ω n = z 1 n = z n = 1

nth roots of unity • Also, zn-1 is the reflection of z 1 in the x axis. • This means that zn-1 is the conjugate pair of z 1 (same x coordinate but one y coordinate is the negative of the other). • So,

nth roots of unity • Therefore, if n is odd, the nth roots of unity occur in conjugate pairs but with one exception: – Which is zn = 1 on the positive x axis as it does not have a conjugate pair (since it has no imaginary part)

nth roots of unity • But, if n is even, the nth roots of unity occur in conjugate pairs with two exceptions: – The first exception is the same as before, i. e. zn = 1 on the positive x axis so it has no conjugate pair – The second exception is when k = n/2. Consider the complex number produced when k = n/2, remembering the general complex nth root is given by:

nth roots of unity – So the second exception is zn/2 = – 1 which is on the negative x axis so again it does not have a conjugate pair

Examples • See scanned examples

nth roots of any complex number r(cosα + isinα) • Let r 1(cosθ + isinθ) be one of the nth roots of r(cosα + isinα). So, • Now compare the LHS to the RHS to find r 1 and θ:

nth roots of r(cosα + isinα) • Considering r 1: • Considering θ and comparing real and imaginary parts of the LHS and RHS:

nth roots of r(cosα + isinα) • We get the same equation twice:

nth roots of r(cosα + isinα) • So if r 1(cosθ + isinθ) is one of the nth roots of r(cosα + isinα) then:

nth roots of r(cosα + isinα) • Taking k = 0, 1, 2, …, n – 1 will obtain all distinct values of θ, and therefore cosθ + isinθ, in the range (we must start with k = 0 rather than k = 1 as in nth roots of unity to obtain the first value):

nth roots of r(cosα + isinα) • The nth roots of r(cosα + isinα) have the properties: – there are n distinct roots of r(cosα + isinα) – the sum of the roots equals zero – that the vectors on an Argand diagram are each separated by equal angles of 2π/n and lie on a circle with a radius of the ‘nth root of r’ – one of the roots has the argument α/n – all of the roots have a modulus of the nth root of r

nth roots of r(cosα + isinα) • However, the nth roots of r(cosα + isinα) do not occur in conjugate pairs since they are not arranged symmetrically about the x axis.

Examples • See scanned examples

In summary – Cube roots of unity • Let cosθ + isinθ be one of the cube roots and use De Moivre’s Theorem to solve: • The three cube roots of unity are:

In summary – Cube roots of unity • Let ω be one of the complex cube roots of unity then: • The three cube roots of unity are 1, ω and ω2 • 1 + ω2 = 0 • ω3 = 1

In summary – nth roots of unity • Let cosθ + isinθ be one of the nth roots and use De Moivre’s Theorem to solve: • The general kth root of unity is:

In summary – nth roots of unity • The nth roots of unity are:

In summary – nth roots of unity • If n is odd then the nth roots of unity occur in conjugate pairs with one exception; zn = 1 (which is a real root). • If n is even the nth roots of unity occur in conjugate pairs with two exceptions; zn = 1 and zn/2 = – 1 (which are both real roots).

In summary – nth roots of unity • If omega, ω, denotes the first complex root of unity then the nth roots of unity are: ω, ω2 , ω3, …, ωr, …, ωn ωn = 1 (Refer to first diagram p 302 of Bostock, Chandler & Rourke text book. )

In summary – nth roots of r(cosα + isinα) • Let r 1(cosθ + isinθ) be one of the nth roots and use De Moivre’s Theorem to solve: • This gives: • where θ is in the range: