02 More Complex Roots.pptx
- Количество слайдов: 43

Complex Numbers More square roots Cubic equations with complex roots Cube root of unity Fourth root of negative unity

Today’s Aims • To find the square root of an imaginary number ni where n is real • To investigate the roots of a cubic equation • To find the cube roots of unity (cube roots of one) and know the standard notation used for them • To understand apply the properties of the cube roots of unity • To find the fourth roots of negative unity
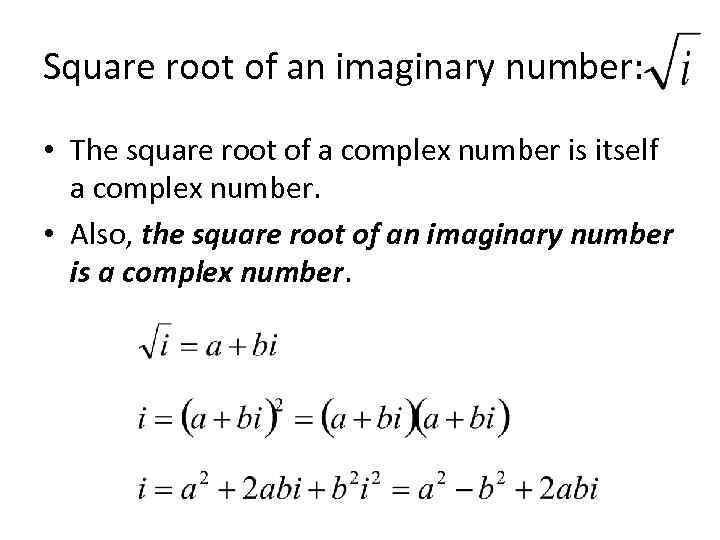
Square root of an imaginary number: • The square root of a complex number is itself a complex number. • Also, the square root of an imaginary number is a complex number.

Square root of an imaginary number: • Comparing coefficients of real and imaginary parts: al re b is
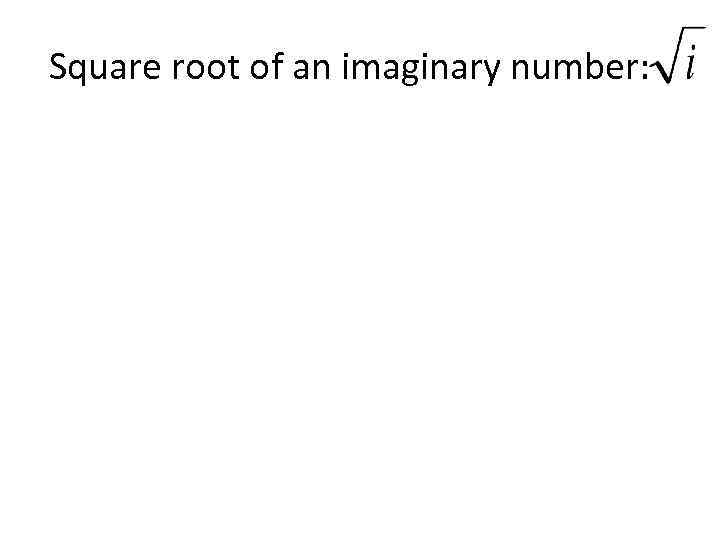
Square root of an imaginary number:
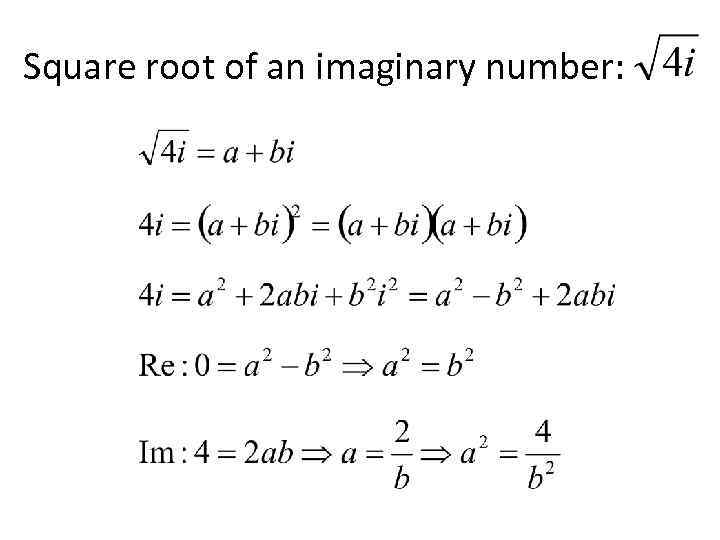
Square root of an imaginary number:

Square root of an imaginary number: bi sr ea l
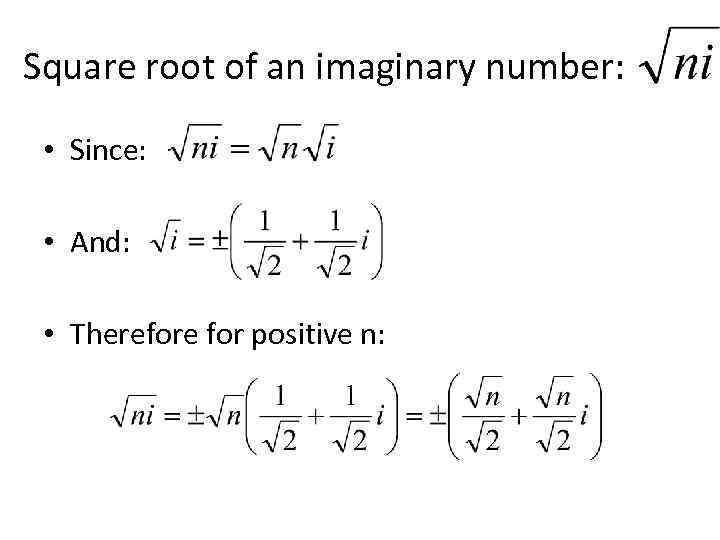
Square root of an imaginary number: • Since: • And: • Therefore for positive n:
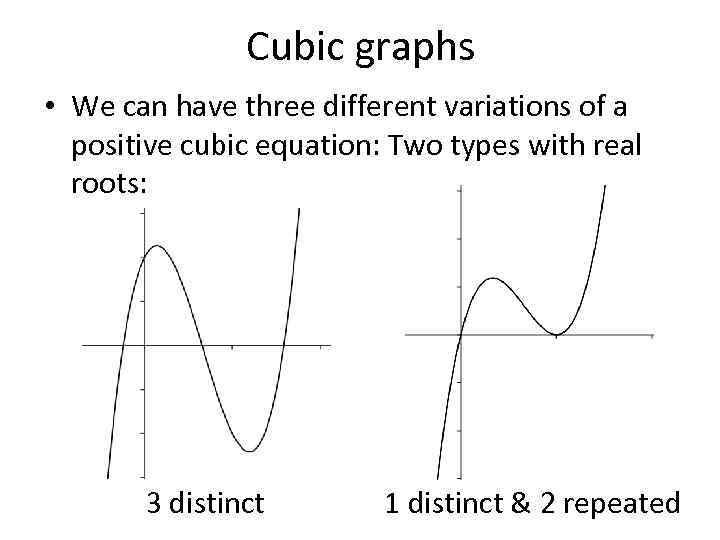
Cubic graphs • We can have three different variations of a positive cubic equation: Two types with real roots: 3 distinct 1 distinct & 2 repeated
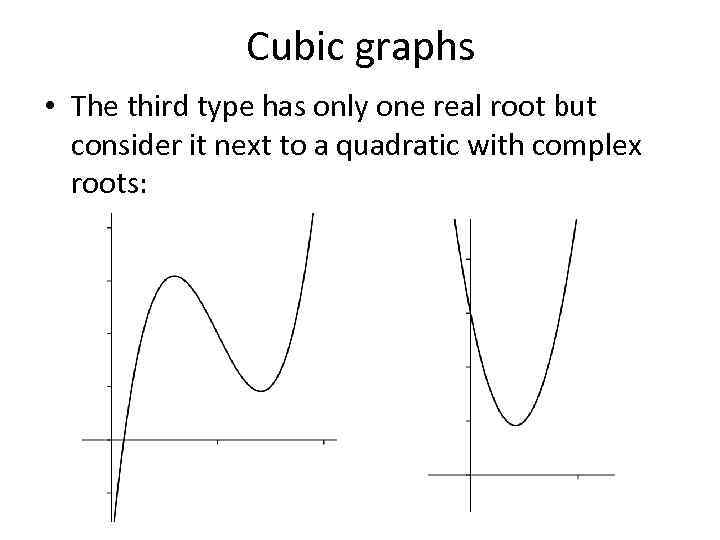
Cubic graphs • The third type has only one real root but consider it next to a quadratic with complex roots:
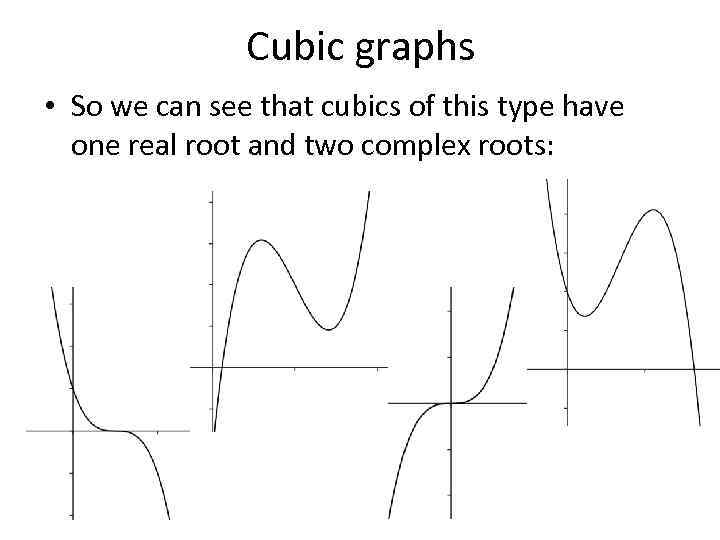
Cubic graphs • So we can see that cubics of this type have one real root and two complex roots:

Cubic equations • If we consider a general factorised cubic equation with one real root we have: a re ex pl m co r 2 ts l o roo rea 1 2 ot l ro • where a, p, q and r are real. • If 2 complex roots they occur in conjugate pairs

Cube roots of unity: • We know that one answer to this is 1 but is the only answer? • We can manipulate this equation to get: • Since one root is x = 1 then, by the factor theorem, (x – 1) is a factor. So our equation becomes:

Cube roots of unity: • We can find p, q and r by long division, comparing coefficients or inspection to get: • Solving the quadratic by the quadratic equation:

Cube roots of unity: • Hence the cube roots of unity are:

Quadratic complex factors • If the roots to a quadratic are α + βi and α – βi, then the complex factors are: – (x – α – βi) and – (x – α + βi) respectively • So for the cube roots of unity:

Cube roots of unity notation and properties • We use the letter omega ω for one of the complex roots. • Now consider ω2:

Cube roots of unity properties • And this is the conjugate pair of ω which is the second complex root.

Cube roots of unity properties • Similarly, if we chose the other complex root for ω, ω2 is still the conjugate pair.

Cube roots of unity properties • Hence the cube roots of unity are given by: 1, ω and ω2 • where ω is the conjugate pair to ω2, • and

Cube roots of unity properties • The first property is that either complex cube root of 1, when squared, gives the other complex root. • The second property is: 1 + ω2 = 0

Application of the cube root of unity properties 1. If 1, ω and ω2 are the cube roots of unity, find i. ω6 ii. ω5 + ω7 iii. (ω9 + ω8)3

Solution to 1 1 i) Since ω is a cube root of unity, ω6 = ω3ω3 = (ωω2) and ω2 are a conjugate pair: So ω6 = ω3ω3 = (ωω2) = 1

Solution to 1 1 ii) Since ω is a cube root of unity, then ω3 = 1 and 1 + ω2 = 0. Also ω5 = ω3ω2 = ω2 and ω7 = ω3ω3ω = ω So, ω5 + ω7 = ω2 + ω = – 1

Solution to 1 1 iii) Since ω is a cube root of unity, then ω3 = 1 and 1 + ω2 = 0. Also ω9 = ω3ω3ω3 = 1 and ω8 = ω3ω3ω2 = ω 2 So (ω9 + ω8)3 = (1 + ω2)3 = (–ω)3 = –ω3 = – 1

Application of the cube root of unity properties 2. Express z 3 + 6 z 2 + 12 z + 7 in the form (z + a)3 + b = 0 and hence solve.

Solution to 2 • Using the binomial theorem: (z + a)3 = z 3 + 3 z 2 a + 3 za 2 + a 3 So, (z + a)3 + b = z 3 + 3 z 2 a + 3 za 2 + a 3 + b Comparing coefficients with z 3 + 6 z 2 + 12 z + 7: 3 a = 6 3 a 2 = 12 a 3 + b = 7 a=2 23 + b = 7 b = – 1

Solution to 2 Hence, z 3 + 6 z 2 + 12 z + 7 = (z + 2)3 – 1 = 0 Now let z + 2 = x so, x 3 – 1 = 0 The cube roots of unity are:

Solution to 2 However x = z + 2 therefore,

Application of factorising complex quadratic roots 3. Form the equation with the roots 1 + i, 1 – i and 2.

Solution to 3 A root of 2 corresponds to a factor of (x – 2) A root of 1 – i corresponds to a factor of (x – (1 – i)) = (x – 1 + i) A root of 1 + i corresponds to a factor of (x – (1 + i)) = (x – 1 – i)

Solution to 3 To obtain an equation with these roots we must multiply the factors together:

Application of factorising complex quadratic roots 4. One root of the equation x 2 + px + q = 0 is 2 – 3 i. Find the values of p and q.

Solution to 4 Since one root is 2 – 3 i then the other root must be the conjugate pair 2 + 3 i. Also any quadratic can be written as: x 2 – (sum of roots)x + (product of roots) = 0 Comparing this with x 2 + px + q = 0: p = – (sum of roots) q = (product of roots)

Solution to 4 sum of roots = 2 – 3 i + 2 + 3 i = 4 product of roots = (2 – 3 i)(2 + 3 i) = 4 + 9 = 13 Therefore, p = – 4 and q = 13 Hence, x 2 – 4 x + 13 = 0
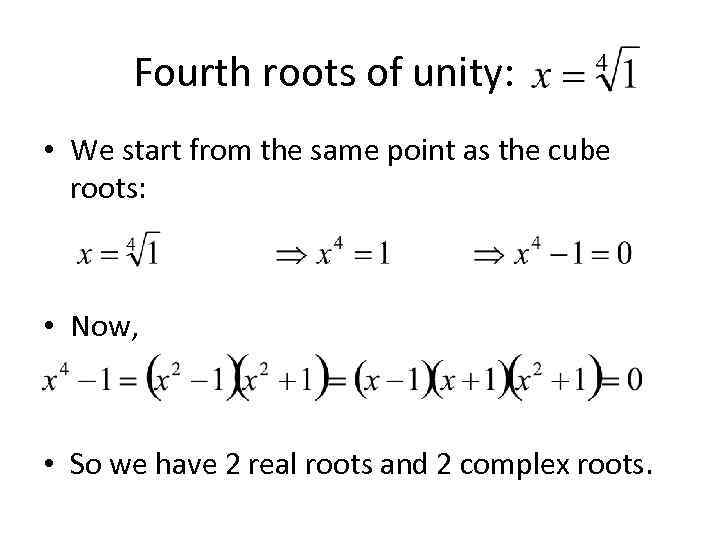
Fourth roots of unity: • We start from the same point as the cube roots: • Now, • So we have 2 real roots and 2 complex roots.

Fourth roots of unity: • The real roots are x = 1 and x = – 1 • The complex roots are: • So the roots are: 1, – 1, i and –i. • Also notice that if ω = i, then ω2 = – 1 and ω3 = –i.

Fourth roots of unity: • Hence the fourth roots of unity are: x = 1, ω, ω2 and ω3 • where ω = i and 1 + ω2 + ω3 = 0.
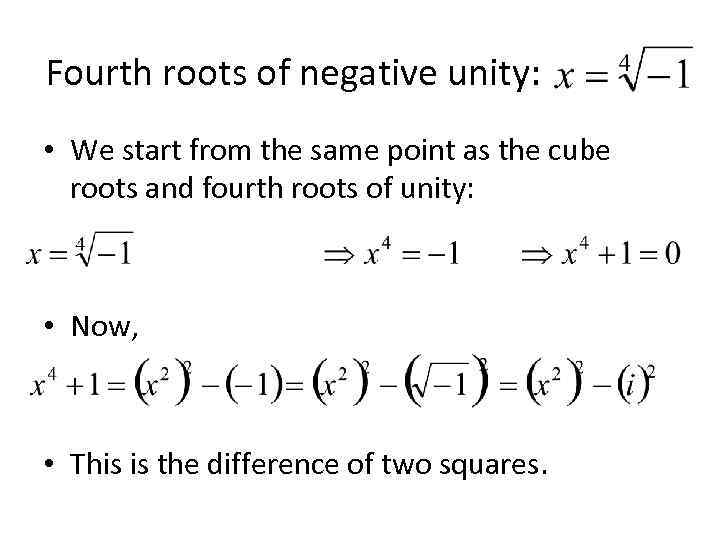
Fourth roots of negative unity: • We start from the same point as the cube roots and fourth roots of unity: • Now, • This is the difference of two squares.
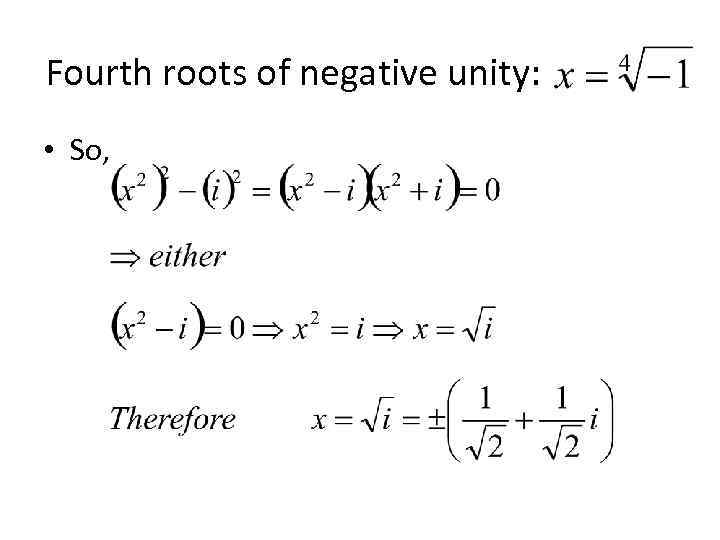
Fourth roots of negative unity: • So,
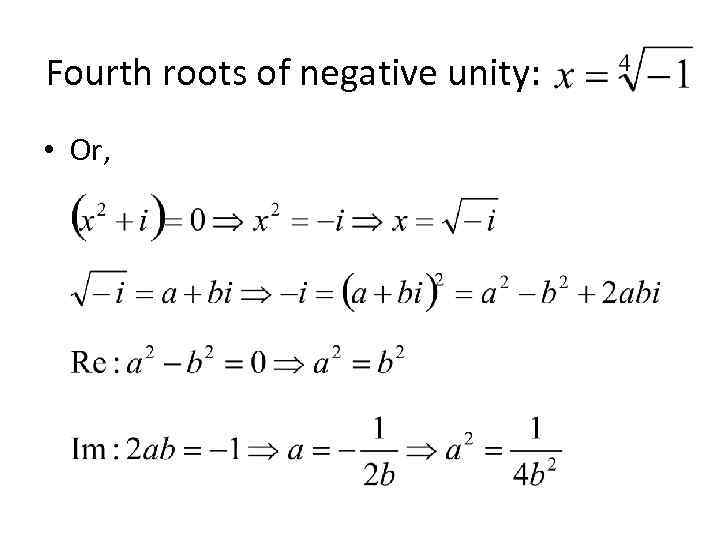
Fourth roots of negative unity: • Or,
Fourth roots of negative unity: • So, bi sr ea l

Fourth roots of negative unity: • Hence the fourth roots of negative unity are:
02 More Complex Roots.pptx