05a De Moivres Theorem More Examples.pptx
- Количество слайдов: 16

Complex Numbers More Examples using De Moivre’s Theorem

De Moivre’s Theorem • De Moivre’s Theorem states that, for all real values of n, • So for any complex number,

Example 1 • Write (1 + √ 3 i)3 as a single complex number in polar form. For polar form we need to find the modulus and the argument: |1 + √ 3 i| = 2 arg(1 + √ 3 i) = arctan(√ 3) = π/3 So, 1 + √ 3 i = 2(cos(π/3) + isin(π/3)) Therefore, (1 + √ 3 i)3 = (2(cos(π/3) + isin(π/3))) 3

Example 1 So, (1 + √ 3 i)3 = 23(cos(π/3) + isin(π/3)) 3 Using De Moivre’s Theorem: (1 + √ 3 i)3 = 23(cos(3π/3) + isin(3π/3)) Hence, (1 + √ 3 i)3 = 8(cos(π) + isin(π))

Example 2 • Find an identity for sin 7θ. • First we consider, • Now expand using the binomial theorem:
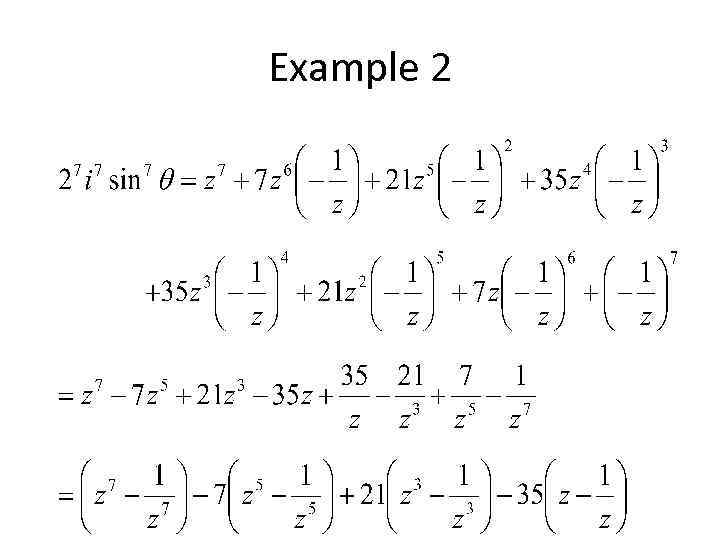
Example 2

Example 2 • Now using, • For n = 7, 5, 3 and 1 we have,

Example 2 • Now i 7 = –i, 27 = 128 and taking 2 i out as a factor on the RHS we have, • Hence,

Example 3 Show that the following identity where t = tanθ. Use this result to solve the equation:

Example 3 Consider, And expand the RHS using De Moivre’s theorem since:

Example 3 So using (where c = cosθ and s = sinθ), Then,

Example 3 So, Therefore,

Example 3 Now divide through by c 4 (remembering that c = cosθ and s = sinθ and also t = tanθ). Hence, as required,

Example 3 Now considering the equation: We can rearrange this to give:

Example 3 Therefore: We can solve this equation rather than the original equation:

Example 3 Now we want solutions for t (= tanθ) not for θ. Also since tanθ has a period of π then we chose values of n to find all solutions from 0 to π since beyond that tanθ will be repeated. Taking n = 0, 1, 2 and 3:
05a De Moivres Theorem More Examples.pptx