Complex Numbers Introduction Powers of i Basic manipulation Conjugate complex numbers Equality
Today’s Aims • To know the definition of a complex number and the corresponding set of complex numbers • To simplify in where i is the unit imaginary number √( – 1) and n is an integer • To add, subtract and multiply to complex numbers • To know the definition, notation and the product property of a conjugate complex number • To divide complex numbers using a conjugate • To understand apply the equality law of complex numbers
A real number • A real number is a number whose square is positive. • A real number can be positive or negative • A real number can be an integer, rational or irrational – e. g. 2, – 5, 0. 6, 5/7, √ 3
An imaginary number • We have already encountered imaginary numbers; these are numbers whose squares are negative, e. g. • Since • Imaginary numbers can be written in the form ni where n is a real number and • For example or • Notice that if n is an integer then we write it before i but if n is a surd then we write it after i.
Definition of a complex number • When a real number and an imaginary number are added or subtracted, the expression so formed, which cannot be simplified, is called a complex number, – e. g. 2 + 3 i, – 4 + 7 i, – 6 – i√ 5 • A general complex number is a + bi where a and b can have any real value including zero
The set of complex numbers • Just as we have notation to denote – the set of natural numbers – the set of integers – the set of rational numbers – the set of real numbers • We also have the set of complex numbers C
Powers of i • To calculate powers of i then we simply use • and multiply out • Negative indices can be treated in the same way • Example…
Adding and Subtracting • To add or subtract complex numbers we split them into their real parts and imaginary parts • Then add or subtract the real part • Then add or subtract the imaginary part • Give your final answer in the form a + bi • Example…
Multiplying • To multiply complex numbers we start by expanding the brackets as usual for real algebraic brackets • Then remember that i 2 is – 1 • Then gather like terms; the real numbers together and the imaginary numbers together • Finally simplify and give your final answer in the form a + bi • Example…
A conjugate complex number • If we have a complex number z = a + bi, then the conjugate of z is given by • z* = a – bi or • z = a – bi
Product property of a conjugate complex number • If z = a + bi, then consider zz* (the product of z and its conjugate z*: • Hence, • Example…
Dividing • When dividing complex numbers remember that: • We can use the conjugate of the denominator to eradicate the imaginary number in the denominator.
Dividing • So, • Notice we have given the answer in the form of α + βi • Example…
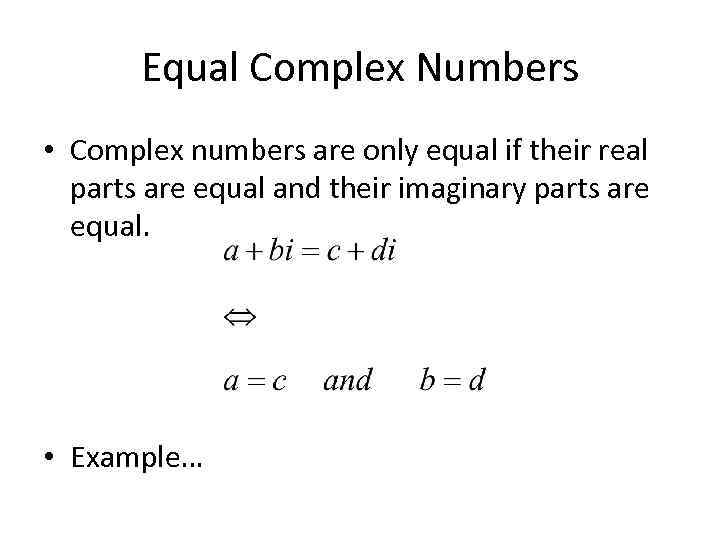
Equal Complex Numbers • Complex numbers are only equal if their real parts are equal and their imaginary parts are equal. • Example…
Using the equality property • We can use this equality property to equate coefficients as an alternative method when dividing complex numbers. • Example… • We can also use it to equate coefficients when finding the square root of a complex number. • Example…
More examples…
Скачать презентацию Complex Numbers Introduction Powers of i Basic manipulation
01 Introduction.pptx