Complex Numbers Greatest and least values of z

Complex Numbers Greatest and least values of |z 1 + z 2| (also known as triangular inequalities) Exponential form Find roots in exponential form

Objectives • To find and use the greatest value of |z 1 + z 2|. • To find and use the least value of |z 1 + z 2|. • To know and use the exponential form of a general complex number. • To find roots of real or complex numbers in exponential form.

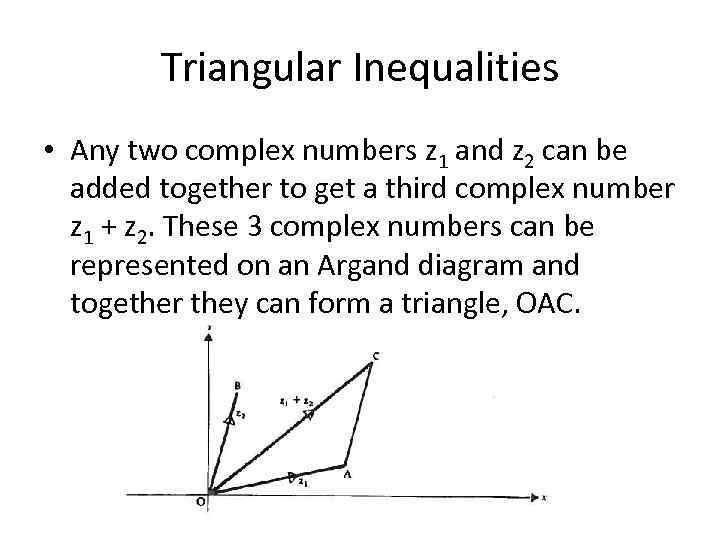
Triangular Inequalities • Any two complex numbers z 1 and z 2 can be added together to get a third complex number z 1 + z 2. These 3 complex numbers can be represented on an Argand diagram and together they can form a triangle, OAC.

Triangular Inequalities • In any triangle the sum of the lengths of any two sides is greater than the length of the third side. • | z 1|, | z 2| and | z 1 + z 2 | are the lengths of the sides of triangle OAC. • So, the following inequality is true: | z 1 + z 2 | < | z 1 | + | z 2 |

Triangular Inequalities • In the special case where z 1 and z 2 are parallel then | z 1 + z 2 | = | z 1| + | z 2|. • So we can conclude that, | z 1 + z 2 | ≤ | z 1 | + | z 2 | • And therefore the greatest value of | z 1 + z 2 | is | z 1| + | z 2|.

Triangular Inequalities • Using the same argument we have two further inequalities: Ø | z 1 | ≤ | z 1 + z 2 | + | z 2 | Ø | z 2 | ≤ | z 1 + z 2 | + | z 1 | • Manipulating each of these we get: Ø | z 1 | – | z 2 | ≤ | z 1 + z 2 | Ø | z 2 | – | z 1 | ≤ | z 1 + z 2 |

Triangular Inequalities • Combining the last two inequalities we conclude that: || z 1| – | z 2|| ≤ | z 1 + z 2 | • Note that on the LHS the outer usage of the modulus symbols || denotes the positive difference between z 1 and z 2 rather than denoting the magnitude as in the remainder of this inequality.

Triangular Inequalities • Therefore the least value of | z 1 + z 2 | is || z 1| – | z 2||. • Combining the least and the greatest values we have: || z 1| – | z 2|| ≤ | z 1 + z 2 | ≤ | z 1| + | z 2| || z 1| – | z 2|| can also be written as| z 1| ~ | z 2|

Example If z 1 = 3 + 4 i and |z 2| = 13, find the greatest and least values of |z 1 + z 2|. |z 1| = √(32 + 42) = 5 || z 1| – | z 2|| = |13 – 5| = 8 (least value) | z 1| + | z 2| = 13 + 5 = 18 (greatest value) Hence, 8 ≤ |z 1 + z 2| ≤ 13

Exponential form • We have seen the Cartesian and the polar forms of complex numbers, now we will consider another form called the exponential form. • We will consider the series expansions of cosθ, sinθ and eθ but we do not have to derive these expansions.

Exponential form • Consider the series expansion of cosθ: • Consider the series expansion of sinθ:

Exponential form • Now consider part of the polar form of a complex number, (cosθ + isinθ), and combine the above two expansions: • Now we will consider the series expansion of the exponential function and compare the two.

Exponential form • The series expansion of the eθ is: • Now consider eiθ :

Exponential form • Simplifying the powers of i we get: • Comparing this result with our earlier result:

Exponential form • We arrive at Euler’s formula: • We can now use this result in the polar form of a complex number to express a complex number in exponential form:

Exponential form • Hence the exponential form of a complex number is:

Examples Express the following in exponential form and draw an Argand diagram: 1. 2. 3. 4. z=1+i z = √ 3 – i z = (1 + i)/(√ 3 – i) (quotient) z = (1 + i)(√ 3 – i) (product)

Example solutions 1. For exponential form we must find r and θ. y (1, 1) π/4 x

Example solutions 2. For exponential form we must find r and θ. y π/6 x (√ 3, -1)

Example solutions 3. We must use the quotient properties to find r and θ.

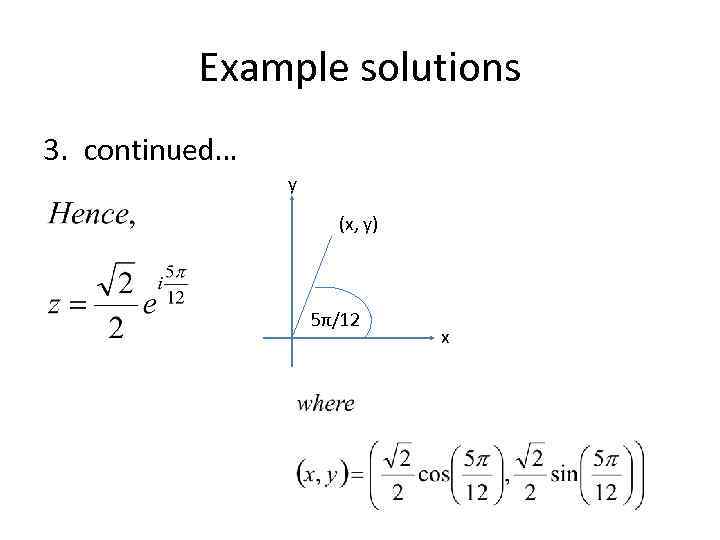
Example solutions 3. continued… y (x, y) 5π/12 x

Example solutions 4. We must use the product properties to find r and θ.

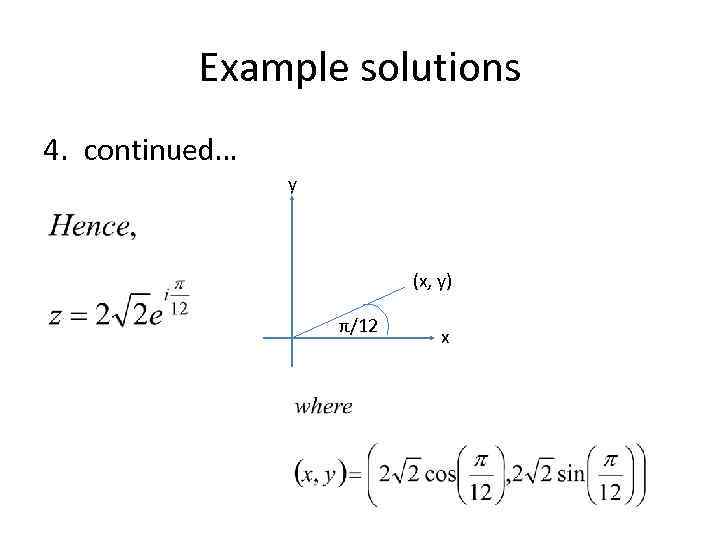
Example solutions 4. continued… y (x, y) π/12 x

Finding roots using the exponential form • We can also use the exponential form to find the roots of real and complex numbers. • The method consists of four parts: 1. Write the real number or complex number in exponential form reiθ evaluating r and θ accordingly. 2. Let r 1 eiα be one of the roots. 3. Raise r 1 eiα to the appropriate power and compare with the exponential form found in 1 to find r 1 and a general solution for α. 4. Use the general solution for α to find the particular solutions thus finding all of the roots.

Finding roots using the exponential form • Regarding the general solution mentioned above, we should use the following formula: • • where θ = arg(z) and –π < θ ≤ π and n is the root (e. g. for a cube root, n = 3) and k is an integer Values of k should be chosen to find all of the roots in the range –π < α ≤ π

Example Find the cube roots of – 1 in exponential form. 1. If z = – 1 then (– 1, 0) gives r = 1 and θ = π. So exponential form is z = eiπ. 2. Let r 1 eiα be a cube root of z. 3. So, (r 1 eiα)3 = z. Thus (r 1 eiα)3 = eiπ. From this we get that r 1 = 1 and 3 iα = iπ. So, 3α = π + 2 kπ where k is an integer. This leads to the general solution α = π/3 + 2 kπ/3.

Example 4. Using the general solution α = π/3 + 2 kπ/3 and choosing values of k to obtain all values of α in the range –π < α ≤ π we have: k = 0: α = π/3 k = 1: α = π k = – 1: α = – π/3

Example • So from part 2. the cube root of – 1 is r 1 eiα • from part 3. r 1 = 1. • and from part 4. α = – π/3, π, π/3 • Hence the cube roots of – 1 in exponential form are:

Example Find the fifth roots of – 1 – i in exponential form. 1. If z = – 1 – i then (– 1, – 1) gives r = √ 2 and θ = – 3π/4 (referring to the Argand diagram). So exponential form is z = √ 2 e–i(3π/4). 2. Let r 1 eiα be a fifth root of z. 3. So, (r 1 eiα)5 = z. Thus (r 1 eiα)5 = √ 2 e–i(3π/4).

Example 4. Using the general solution and appropriate values of k to find all values of α in the range –π < α ≤ π we have:

Example • So from part 2. the cube root of – 1 – i is r 1 eiα • from part 3. r 1 = 10√ 2. • and from part 4. α = – 19π/20, – 11π/20, – 3π/20, π/4, 13π/20 • Hence the cube roots of – 1 – i in exponential form are:

In summary • The greatest and least values of | z 1 + z 2 | are: || z 1| – | z 2|| ≤ | z 1 + z 2 | ≤ | z 1| + | z 2| • The exponential form of a complex number is: z = reiθ where r = |z| and θ = arg(z)

In summary • When finding roots in exponential form, r 1 eiα , the general solution of α is: – where θ = arg(z) and –π < θ ≤ π – and n is the root (e. g. for a cube root, n = 3) – and k is an integer – Note that values of k should be chosen to find all of the roots in the range –π < α ≤ π unless otherwise stated.