05 De Moivres Theorem and Applications.pptx
- Количество слайдов: 40

Complex Numbers De Moivre’s Theorem Applications of De Moivre’s Theorem

Objectives • To know De Moivre’s Theorem • To apply De Moivre’s Theorem to prove trigonometric identities

De Moivre’s Theorem • De Moivre’s Theorem states that, for all real values of n, • We will show this deductively for positive integral values of n and we will prove it inductively for all n.

Deductively (n is a positive integer) • Let z = cosθ + isinθ – where r = |z| = 1 and arg(z) = θ • Consider z 2 = zz: – |z 2 | = |zz| = |z||z| = 1 – arg(z 2) = arg(zz) = arg(z) + arg(z) = θ + θ = 2θ – So z 2 = 1(cos 2θ + isin 2θ) = cos 2θ + isin 2θ

Deductively (n is a positive integer) • Consider z 3 = zz 2: – |z 3 | = |zz 2| = |z||z 2| = 1 – arg(z 3) = arg(zz 2) = arg(z) + arg(z 2) = θ + 2θ = 3θ – So z 3 = 1(cos 3θ + isin 3θ) = cos 3θ + isin 3θ • These two results suggest that for positive integral values of n, – zn = cosnθ + isinnθ
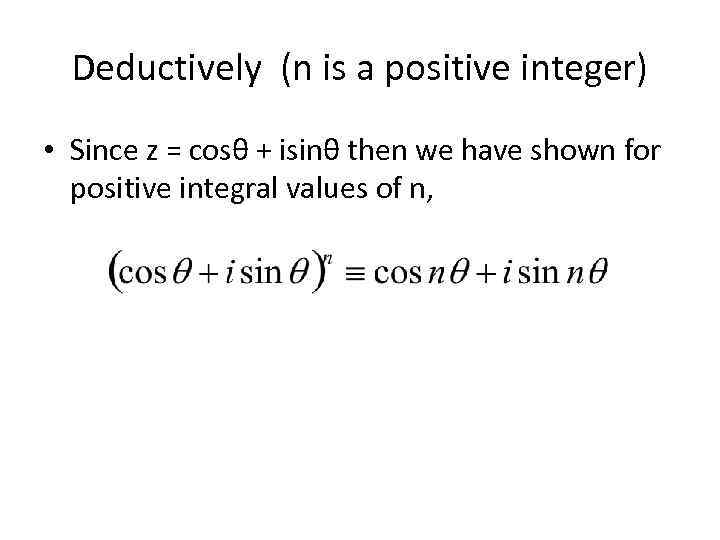
Deductively (n is a positive integer) • Since z = cosθ + isinθ then we have shown for positive integral values of n,

Inductively • We will now use an inductive method to prove De Moivre’s theorem for all n: – When n is a positive integer – When n is a negative integer – When n is rational

Inductive proof when n is a positive integer • If pn is the statement • Then pk is the statement

Inductive proof when n is a positive integer • This implies that pk+1 is the statement

Inductive proof when n is a positive integer • Hence, • Now consider p 1 which is obviously true. • Using both points above we can conclude that pn is true for all positive integral values of n.
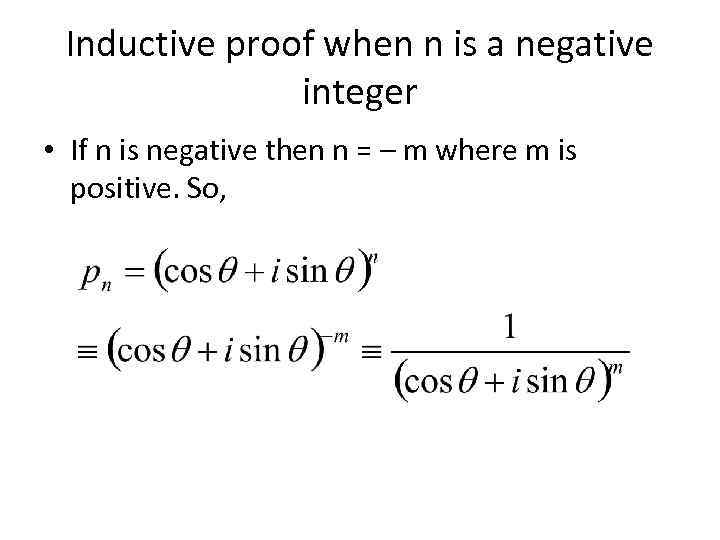
Inductive proof when n is a negative integer • If n is negative then n = – m where m is positive. So,
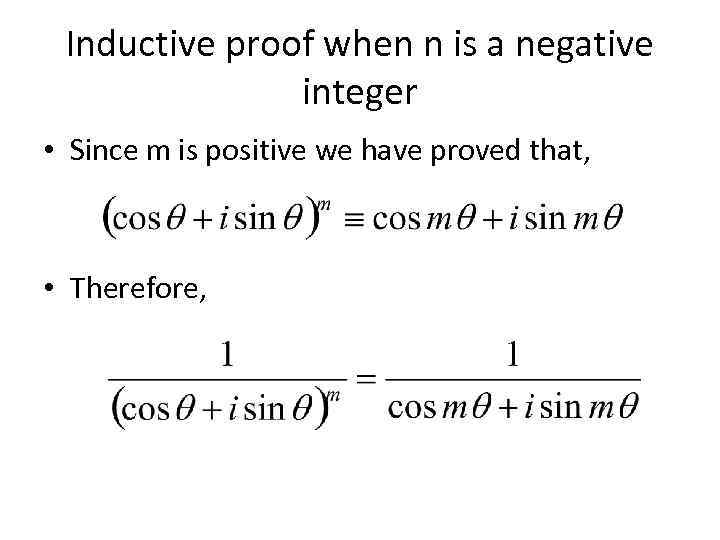
Inductive proof when n is a negative integer • Since m is positive we have proved that, • Therefore,
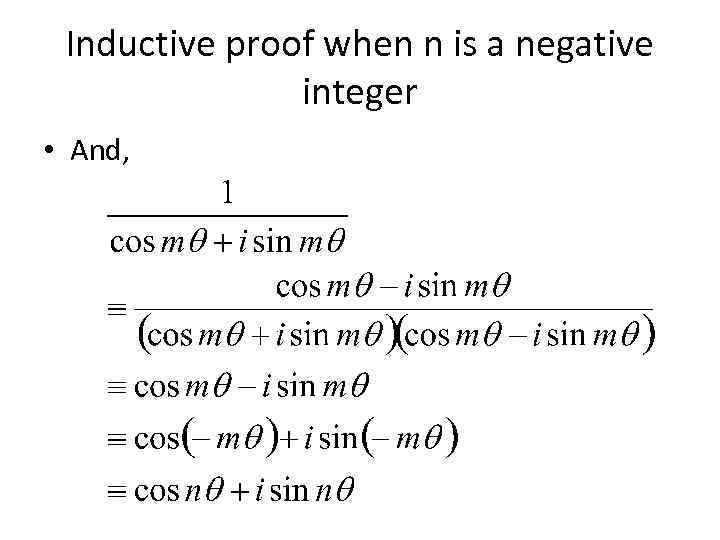
Inductive proof when n is a negative integer • And,

Inductive proof when n is a negative integer • So when n = – m where m is positive, • And we can conclude that pn is true for all negative integral values of n.
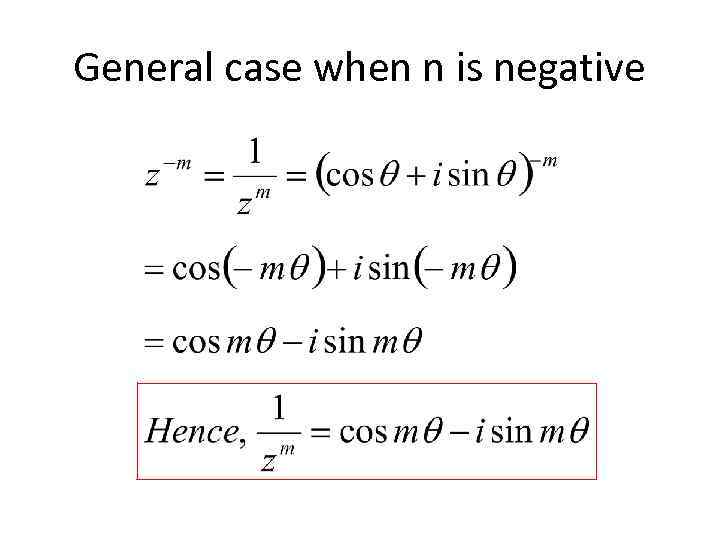
General case when n is negative
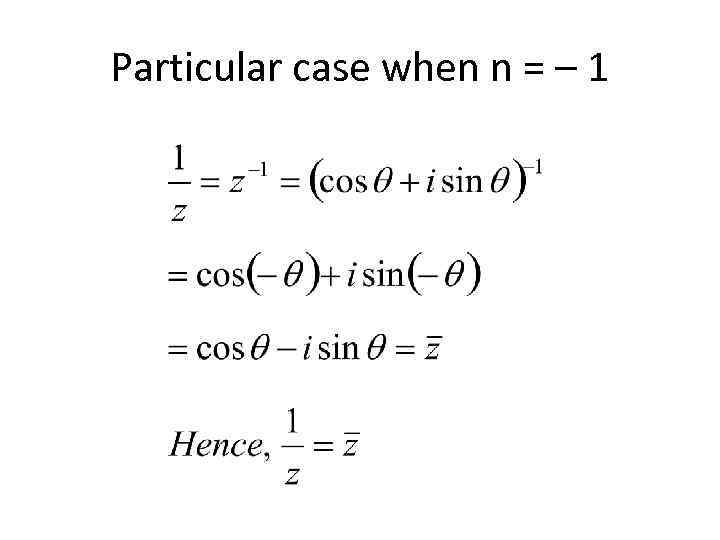
Particular case when n = – 1

Inductive proof when n is rational • If n is rational then n = p/q where p and q are integers. • We wish to prove that

Inductive proof when n is rational • Raising the RHS to the power of q: • As q is an integer, and • As p is an integer.

Inductive proof when n is rational • So, • Now take the qth root of each side, • And we can conclude that pn is true for all rational values of n.

Properties of z and 1/z • We have seen that, • Hence,

Properties of z and 1/z • Also using De Moivre’s Theorem, • Hence,

Applications of De Moivre’s Theorem • We can use De Moivre’s Theorem to express multiple angle trigonometric functions, such as sin(nθ), cos(nθ) or tan(nθ), in terms of single angle forms, i. e. sinθ, cosθ and tanθ. • We can use De Moivre’s Theorem to expand trigonometric functions raised to an index, i. e. :
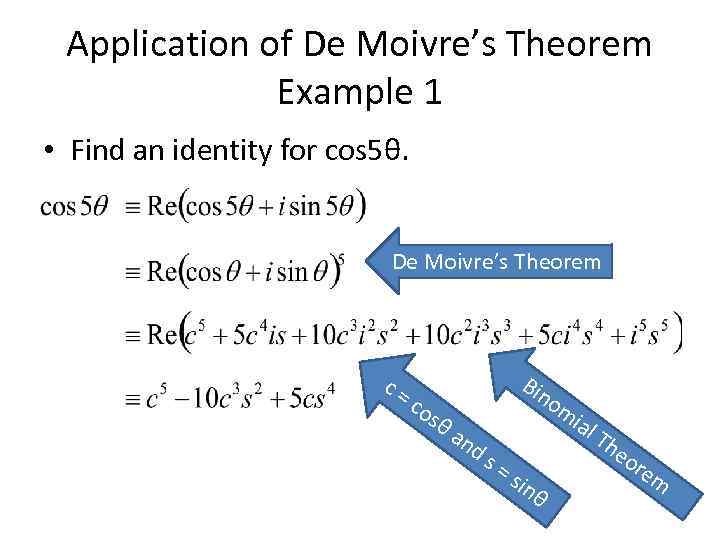
Application of De Moivre’s Theorem Example 1 • Find an identity for cos 5θ. De Moivre’s Theorem c= co sθ Bin an ds om =s inθ ial Th e or e m

Application of De Moivre’s Theorem Example 1 • Hence, • This can be written entirely in terms of cosθ by using cos 2θ + sin 2θ = 1.
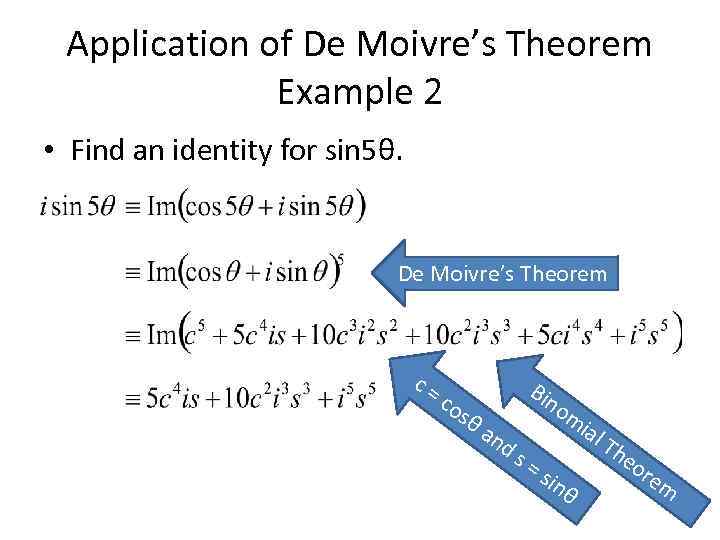
Application of De Moivre’s Theorem Example 2 • Find an identity for sin 5θ. De Moivre’s Theorem c= co sθ Bin an ds om =s inθ ial Th e or e m

Application of De Moivre’s Theorem Example 2 • Hence, • This can be written entirely in terms of sinθ by using cos 2θ + sin 2θ = 1.

Application of De Moivre’s Theorem Example 3 • The above two identities can be combined to find tan 5θ: • Divide all terms by cos 5θ to give:

Application of De Moivre’s Theorem Example 4 • Prove that: • Using De Moivre’s Theorem we know that:

Application of De Moivre’s Theorem Example 4 • So,

Application of De Moivre’s Theorem Example 5 • Hence using the above result simplify:

Application of De Moivre’s Theorem Example 5 • So,

Application of De Moivre’s Theorem Example 5 • Now using the result found in example 4: • Hence,

Application of De Moivre’s Theorem Example 6 • Find an identity for cos 4θ by considering • So, • Now expand using the binomial theorem:

Application of De Moivre’s Theorem Example 6

Application of De Moivre’s Theorem Example 6 • Now using, • For n = 4 and n = 2 we have,

Application of De Moivre’s Theorem Example 6 • Hence,

In summary • De Moivre’s Theorem is: • And if z = cosθ + isinθ,

In summary • To find cosnθ then consider the real part of zn, i. e. : • To find sinnθ then consider the imaginary part of zn, i. e. :

In summary • To find cosnθ consider: • And:

In summary • To find sinnθ consider: • And:
05 De Moivres Theorem and Applications.pptx