Complex Algebra Review Dr. V. Këpuska
Complex Algebra Elements u Definitions: u Note: Real numbers can be thought of as complex numbers with imaginary part equal to zero. 3/17/2018 Veton Këpuska 2
Complex Algebra Elements 3/17/2018 Veton Këpuska 3
Euler’s Identity 3/17/2018 Veton Këpuska 4
Polar Form of Complex Numbers u Magnitude of a complex number z is a generalization of the absolute value function/operator for real numbers. It is buy definition always non-negative. 3/17/2018 Veton Këpuska 5
Polar Form of Complex Numbers u Conversion between polar and rectangular (Cartesian) forms. u For z=0+j 0; called “complex zero” one can not define arg(0+j 0). Why? 3/17/2018 Veton Këpuska 6
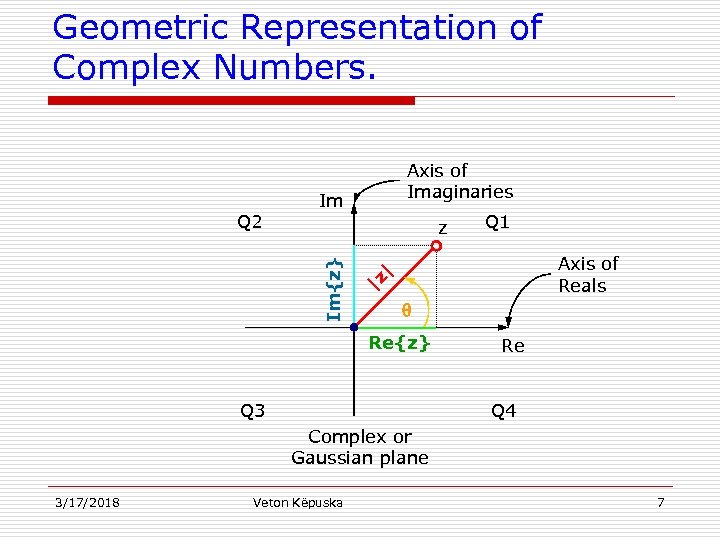
Geometric Representation of Complex Numbers. Im z Q 1 Axis of Reals |z | Im{z} Q 2 Axis of Imaginaries Re{z} Q 3 Re Q 4 Complex or Gaussian plane 3/17/2018 Veton Këpuska 7
Geometric Representation of Complex Numbers. Arg{z} ≥ 0 Q 3 or Q 4 Arg{z} ≤ 0 Q 1 or Q 4 Re{z} ≤ 0 Q 2 Re{z} ≥ 0 Q 2 or Q 3 Im{z} ≥ 0 3/17/2018 Im Im{z} ≤ 0 Axis of Reals | Q 1 or Q 2 Axis of Imaginarie s z Q 1 Condition 2 |z Condition 1 Im{z} Complex Number in Quadrant Re{z} Q 3 Re Q 4 Complex or Gaussian plane Veton Këpuska 8
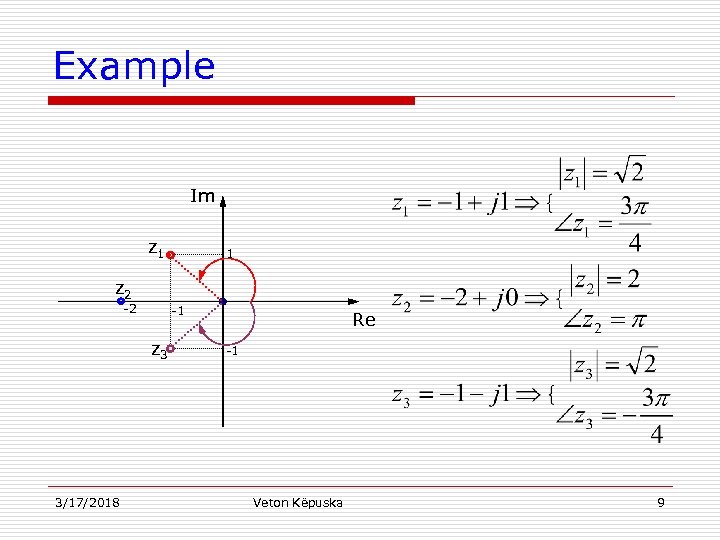
Example Im z 1 1 z 2 -2 -1 z 3 3/17/2018 Re -1 Veton Këpuska 9
Conjugation of Complex Numbers u Definition: If z = x+jy ∈ C then z* = x-jy is called the “Complex Conjugate” number of z. u Example: If z=rej (polar form) then what is z* also in polar form? If z=rej then z*=re-j 3/17/2018 Veton Këpuska 10
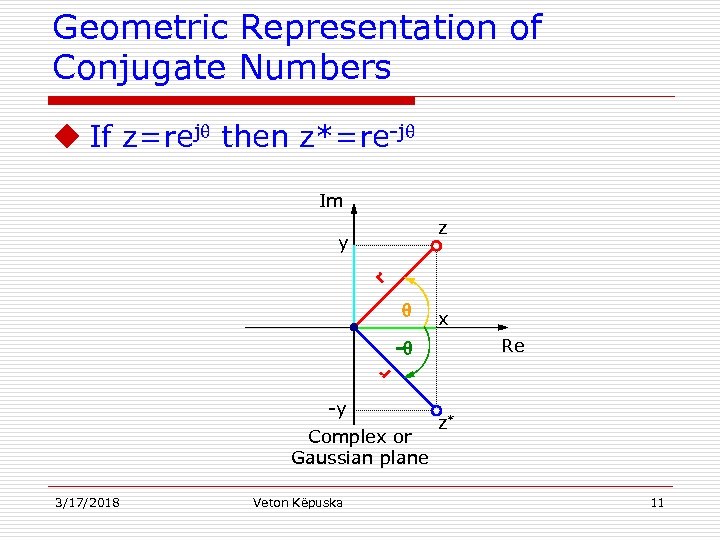
Geometric Representation of Conjugate Numbers u If z=rej then z*=re-j Im z r y x Re r - -y Complex or Gaussian plane 3/17/2018 Veton Këpuska z* 11
Complex Number Operations u Extension of Operations for Real Numbers u When adding/subtracting complex numbers it is most convenient to use Cartesian form. u When multiplying/dividing complex numbers it is most convenient to use Polar form. 3/17/2018 Veton Këpuska 12
Addition/Subtraction of Complex Numbers 3/17/2018 Veton Këpuska 13
Multiplication/Division of Complex Numbers 3/17/2018 Veton Këpuska 14
Useful Identities u z ∈ C, ∈ R & n ∈ Z (integer set) 3/17/2018 Veton Këpuska 15
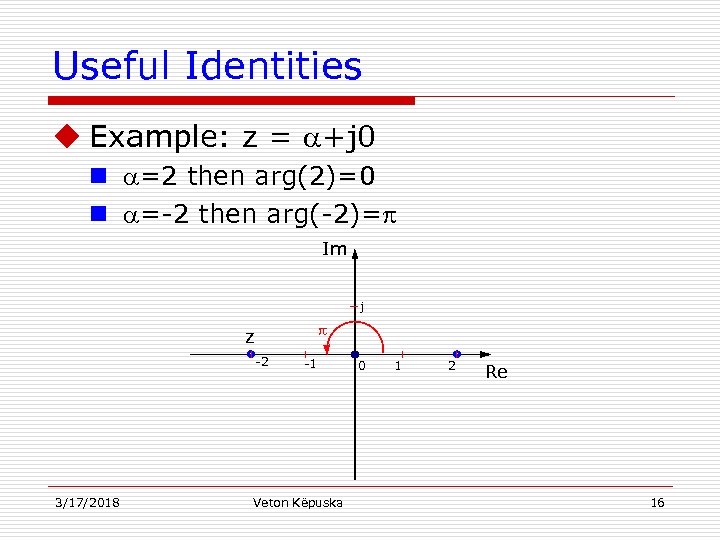
Useful Identities u Example: z = +j 0 n =2 then arg(2)=0 n =-2 then arg(-2)= Im j z -2 3/17/2018 -1 Veton Këpuska 0 1 2 Re 16
Silly Examples and Tricks Im j /2 -1 3 /2 0 1 Re -j 3/17/2018 Veton Këpuska 17
Division Example u Division of two complex numbers in rectangular form. 3/17/2018 Veton Këpuska 18
Roots of Unity u Regard the equation: z. N-1=0, where z ∈ C & N ∈ Z+ (i. e. N>0) u The fundamental theorem of algebra (Gauss) states that an Nth degree algebraic equation has N roots (not necessarily distinct). u Example: n N=3; z 3 -1=0 z 3=1 ⇒ 3/17/2018 Veton Këpuska 19
Roots of Unity u z. N-1=0 has roots , k=0, 1, . . , N-1, where u The roots of are called Nth roots of unity. 3/17/2018 Veton Këpuska 20
Roots of Unity u Verification: 3/17/2018 Veton Këpuska 21
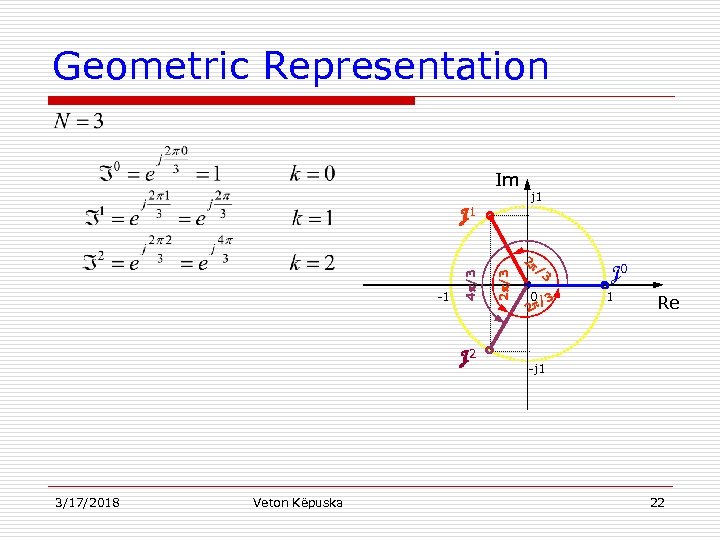
Geometric Representation Im j 1 J 2 3/17/2018 Veton Këpuska 2 /3 -1 4 /3 J 1 2 / 3 0 /3 2 J 0 1 Re -j 1 22
Important Observations 1. Magnitude of each root are equal to 1. Thus, the Nth roots of unity are located on the unit circle. (Unit circle is a circle on the complex plane with radius of 1). 2. The difference in angle between two consecutive roots is 2 /N. 3. The roots, if complex, appear in complex-conjugate pairs. For example for N=3, (J 1)*=J 2. In general the following property holds: JN-k=(Jk)* 3/17/2018 Veton Këpuska 23
Скачать презентацию Complex Algebra Review Dr V Këpuska Complex
52d140f423e6c81cbf6e78422c8b0932.ppt