3e4d0cb9461c4a4b241fc2a1ac7cc991.ppt
- Количество слайдов: 172
 Compiler Design 1
Compiler Design 1
 Course Information • Instructor : Dr. Farhad Soleimanian Gharehchopogh – Email: farhad. soleimanian@gmail. com • Course Web Page: http: //www. soleimanian. net/compiler 2
Course Information • Instructor : Dr. Farhad Soleimanian Gharehchopogh – Email: farhad. soleimanian@gmail. com • Course Web Page: http: //www. soleimanian. net/compiler 2
 Preliminaries Required • Basic knowledge of programming languages. • Basic knowledge of FSA and CFG. • Knowledge of a high programming language for the programming assignments. Textbook: Alfred V. Aho, Monica S. Lam, Ravi Sethi, and Jeffrey D. Ullman, “Compilers: Principles, Techniques, and Tools” Second Edition, Addison-Wesley, 2007. 3
Preliminaries Required • Basic knowledge of programming languages. • Basic knowledge of FSA and CFG. • Knowledge of a high programming language for the programming assignments. Textbook: Alfred V. Aho, Monica S. Lam, Ravi Sethi, and Jeffrey D. Ullman, “Compilers: Principles, Techniques, and Tools” Second Edition, Addison-Wesley, 2007. 3
 Grading • Midterm : 30% • Project : 30% • Final : 40% 4
Grading • Midterm : 30% • Project : 30% • Final : 40% 4
 Course Outline • Introduction to Compiling • Lexical Analysis • Syntax Analysis – Context Free Grammars – Top-Down Parsing, LL Parsing – Bottom-Up Parsing, LR Parsing • Syntax-Directed Translation – Attribute Definitions – Evaluation of Attribute Definitions • Semantic Analysis, Type Checking • Run-Time Organization • Intermediate Code Generation 5
Course Outline • Introduction to Compiling • Lexical Analysis • Syntax Analysis – Context Free Grammars – Top-Down Parsing, LL Parsing – Bottom-Up Parsing, LR Parsing • Syntax-Directed Translation – Attribute Definitions – Evaluation of Attribute Definitions • Semantic Analysis, Type Checking • Run-Time Organization • Intermediate Code Generation 5
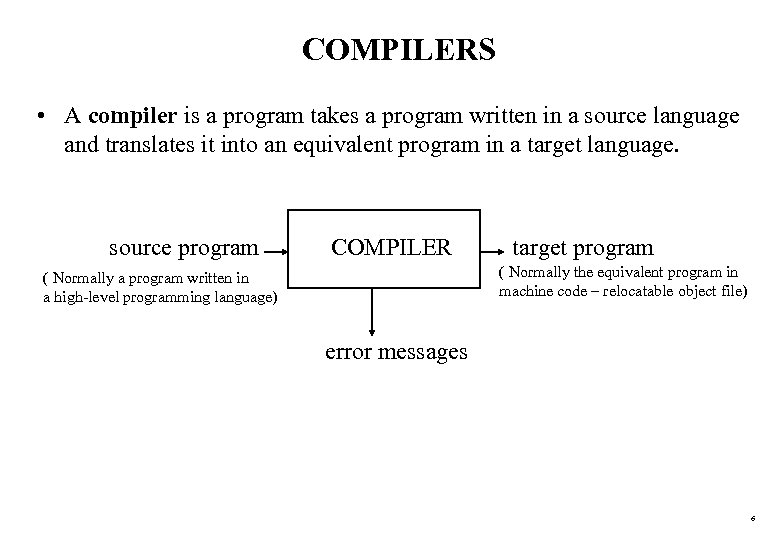 COMPILERS • A compiler is a program takes a program written in a source language and translates it into an equivalent program in a target language. source program COMPILER target program ( Normally the equivalent program in machine code – relocatable object file) ( Normally a program written in a high-level programming language) error messages 6
COMPILERS • A compiler is a program takes a program written in a source language and translates it into an equivalent program in a target language. source program COMPILER target program ( Normally the equivalent program in machine code – relocatable object file) ( Normally a program written in a high-level programming language) error messages 6
 Other Applications • In addition to the development of a compiler, the techniques used in compiler design can be applicable to many problems in computer science. – Techniques used in a lexical analyzer can be used in text editors, information retrieval system, and pattern recognition programs. – Techniques used in a parser can be used in a query processing system such as SQL. – Many software having a complex front-end may need techniques used in compiler design. • A symbolic equation solver which takes an equation as input. That program should parse given input equation. the – Most of the techniques used in compiler design can be used in Natural Language Processing (NLP) systems. 7
Other Applications • In addition to the development of a compiler, the techniques used in compiler design can be applicable to many problems in computer science. – Techniques used in a lexical analyzer can be used in text editors, information retrieval system, and pattern recognition programs. – Techniques used in a parser can be used in a query processing system such as SQL. – Many software having a complex front-end may need techniques used in compiler design. • A symbolic equation solver which takes an equation as input. That program should parse given input equation. the – Most of the techniques used in compiler design can be used in Natural Language Processing (NLP) systems. 7
 Major Parts of Compilers • There are two major parts of a compiler: Analysis and Synthesis • In analysis phase, an intermediate representation is created from the given source program. – Lexical Analyzer, Syntax Analyzer and Semantic Analyzer are the parts of this phase. • In synthesis phase, the equivalent target program is created from this intermediate representation. – Intermediate Code Generator, and Code Optimizer are the parts of this phase. 8
Major Parts of Compilers • There are two major parts of a compiler: Analysis and Synthesis • In analysis phase, an intermediate representation is created from the given source program. – Lexical Analyzer, Syntax Analyzer and Semantic Analyzer are the parts of this phase. • In synthesis phase, the equivalent target program is created from this intermediate representation. – Intermediate Code Generator, and Code Optimizer are the parts of this phase. 8
 Phases of A Compiler Source Program Lexical Analyzer Syntax Semantic Analyzer Intermediate Code Generator Code Optimizer Code Generator Target Program • Each phase transforms the source program from one representation into another representation. • They communicate with error handlers. • They communicate with the symbol table. 9
Phases of A Compiler Source Program Lexical Analyzer Syntax Semantic Analyzer Intermediate Code Generator Code Optimizer Code Generator Target Program • Each phase transforms the source program from one representation into another representation. • They communicate with error handlers. • They communicate with the symbol table. 9
 Lexical Analyzer • Lexical Analyzer reads the source program character by character and returns the tokens of the source program. • A token describes a pattern of characters having same meaning in the source program. (such as identifiers, operators, keywords, numbers, delimeters and so on) Ex: newval : = oldval + 12 => tokens: newval identifier : = oldval + 12 assignment operator identifier add operator a number • Puts information about identifiers into the symbol table. • Regular expressions are used to describe tokens (lexical constructs). • A (Deterministic) Finite State Automaton can be used in the implementation of a lexical analyzer. 10
Lexical Analyzer • Lexical Analyzer reads the source program character by character and returns the tokens of the source program. • A token describes a pattern of characters having same meaning in the source program. (such as identifiers, operators, keywords, numbers, delimeters and so on) Ex: newval : = oldval + 12 => tokens: newval identifier : = oldval + 12 assignment operator identifier add operator a number • Puts information about identifiers into the symbol table. • Regular expressions are used to describe tokens (lexical constructs). • A (Deterministic) Finite State Automaton can be used in the implementation of a lexical analyzer. 10
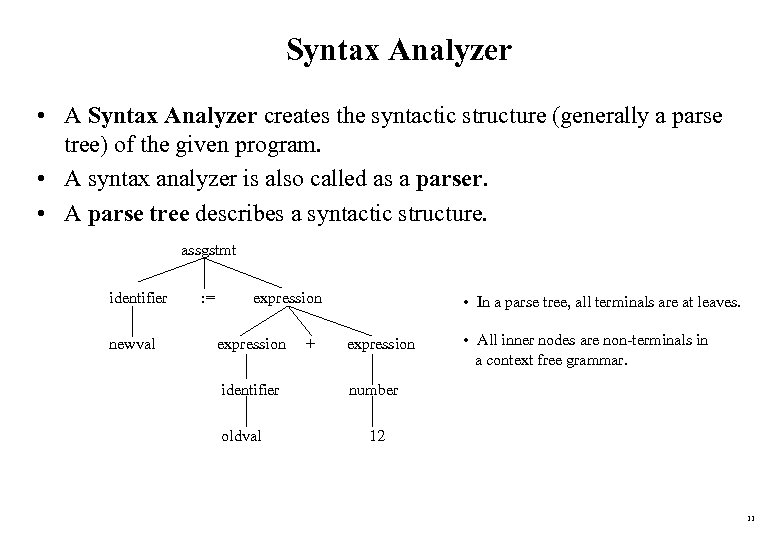 Syntax Analyzer • A Syntax Analyzer creates the syntactic structure (generally a parse tree) of the given program. • A syntax analyzer is also called as a parser. • A parse tree describes a syntactic structure. assgstmt identifier newval : = expression identifier oldval + • In a parse tree, all terminals are at leaves. expression • All inner nodes are non-terminals in a context free grammar. number 12 11
Syntax Analyzer • A Syntax Analyzer creates the syntactic structure (generally a parse tree) of the given program. • A syntax analyzer is also called as a parser. • A parse tree describes a syntactic structure. assgstmt identifier newval : = expression identifier oldval + • In a parse tree, all terminals are at leaves. expression • All inner nodes are non-terminals in a context free grammar. number 12 11
 Syntax Analyzer (CFG) • The syntax of a language is specified by a context free grammar (CFG). • The rules in a CFG are mostly recursive. • A syntax analyzer checks whether a given program satisfies the rules implied by a CFG or not. – If it satisfies, the syntax analyzer creates a parse tree for the given program. • Ex: We use BNF (Backus Naur Form) to specify a CFG assgstmt -> identifier : = expression -> identifier expression -> number expression -> expression + expression 12
Syntax Analyzer (CFG) • The syntax of a language is specified by a context free grammar (CFG). • The rules in a CFG are mostly recursive. • A syntax analyzer checks whether a given program satisfies the rules implied by a CFG or not. – If it satisfies, the syntax analyzer creates a parse tree for the given program. • Ex: We use BNF (Backus Naur Form) to specify a CFG assgstmt -> identifier : = expression -> identifier expression -> number expression -> expression + expression 12
 Syntax Analyzer versus Lexical Analyzer • Which constructs of a program should be recognized by the lexical analyzer, and which ones by the syntax analyzer? – Both of them do similar things; But the lexical analyzer deals with simple non-recursive constructs of the language. – The syntax analyzer deals with recursive constructs of the language. – The lexical analyzer simplifies the job of the syntax analyzer. – The lexical analyzer recognizes the smallest meaningful units (tokens) in a source program. – The syntax analyzer works on the smallest meaningful units (tokens) in a source program to recognize meaningful structures in our programming language. 13
Syntax Analyzer versus Lexical Analyzer • Which constructs of a program should be recognized by the lexical analyzer, and which ones by the syntax analyzer? – Both of them do similar things; But the lexical analyzer deals with simple non-recursive constructs of the language. – The syntax analyzer deals with recursive constructs of the language. – The lexical analyzer simplifies the job of the syntax analyzer. – The lexical analyzer recognizes the smallest meaningful units (tokens) in a source program. – The syntax analyzer works on the smallest meaningful units (tokens) in a source program to recognize meaningful structures in our programming language. 13
 Parsing Techniques • Depending on how the parse tree is created, there are different parsing techniques. • These parsing techniques are categorized into two groups: – Top-Down Parsing, – Bottom-Up Parsing • Top-Down Parsing: – Construction of the parse tree starts at the root, and proceeds towards the leaves. – Efficient top-down parsers can be easily constructed by hand. – Recursive Predictive Parsing, Non-Recursive Predictive Parsing (LL Parsing). • Bottom-Up Parsing: – – – Construction of the parse tree starts at the leaves, and proceeds towards the root. Normally efficient bottom-up parsers are created with the help of some software tools. Bottom-up parsing is also known as shift-reduce parsing. Operator-Precedence Parsing – simple, restrictive, easy to implement LR Parsing – much general form of shift-reduce parsing, LR, SLR, LALR 14
Parsing Techniques • Depending on how the parse tree is created, there are different parsing techniques. • These parsing techniques are categorized into two groups: – Top-Down Parsing, – Bottom-Up Parsing • Top-Down Parsing: – Construction of the parse tree starts at the root, and proceeds towards the leaves. – Efficient top-down parsers can be easily constructed by hand. – Recursive Predictive Parsing, Non-Recursive Predictive Parsing (LL Parsing). • Bottom-Up Parsing: – – – Construction of the parse tree starts at the leaves, and proceeds towards the root. Normally efficient bottom-up parsers are created with the help of some software tools. Bottom-up parsing is also known as shift-reduce parsing. Operator-Precedence Parsing – simple, restrictive, easy to implement LR Parsing – much general form of shift-reduce parsing, LR, SLR, LALR 14
 Semantic Analyzer • A semantic analyzer checks the source program for semantic errors and collects the type information for the code generation. • Type-checking is an important part of semantic analyzer. • Normally semantic information cannot be represented by a context-free language used in syntax analyzers. • Context-free grammars used in the syntax analysis are integrated with attributes (semantic rules) – the result is a syntax-directed translation, – Attribute grammars • Ex: newval : = oldval + 12 • The type of the identifier newval must match with type of the expression (oldval+12) 15
Semantic Analyzer • A semantic analyzer checks the source program for semantic errors and collects the type information for the code generation. • Type-checking is an important part of semantic analyzer. • Normally semantic information cannot be represented by a context-free language used in syntax analyzers. • Context-free grammars used in the syntax analysis are integrated with attributes (semantic rules) – the result is a syntax-directed translation, – Attribute grammars • Ex: newval : = oldval + 12 • The type of the identifier newval must match with type of the expression (oldval+12) 15
 Intermediate Code Generation • A compiler may produce an explicit intermediate codes representing the source program. • These intermediate codes are generally machine (architecture independent). But the level of intermediate codes is close to the level of machine codes. • Ex: newval : = oldval * fact + 1 id 1 : = id 2 * id 3 + 1 MULT ADD MOV id 2, id 3, temp 1, #1, temp 2, , id 1 Intermediates Codes (Quadraples) 16
Intermediate Code Generation • A compiler may produce an explicit intermediate codes representing the source program. • These intermediate codes are generally machine (architecture independent). But the level of intermediate codes is close to the level of machine codes. • Ex: newval : = oldval * fact + 1 id 1 : = id 2 * id 3 + 1 MULT ADD MOV id 2, id 3, temp 1, #1, temp 2, , id 1 Intermediates Codes (Quadraples) 16
 Code Optimizer (for Intermediate Code Generator) • The code optimizer optimizes the code produced by the intermediate code generator in the terms of time and space. • Ex: MULT ADD id 2, id 3, temp 1, #1, id 1 17
Code Optimizer (for Intermediate Code Generator) • The code optimizer optimizes the code produced by the intermediate code generator in the terms of time and space. • Ex: MULT ADD id 2, id 3, temp 1, #1, id 1 17
 Code Generator • Produces the target language in a specific architecture. • The target program is normally is a relocatable object file containing the machine codes. • Ex: ( assume that we have an architecture with instructions whose at least one of its operands is a machine register) MOVE MULT ADD MOVE id 2, R 1 id 3, R 1 #1, R 1, id 1 18
Code Generator • Produces the target language in a specific architecture. • The target program is normally is a relocatable object file containing the machine codes. • Ex: ( assume that we have an architecture with instructions whose at least one of its operands is a machine register) MOVE MULT ADD MOVE id 2, R 1 id 3, R 1 #1, R 1, id 1 18
 Lexical Analyzer • Lexical Analyzer reads the source program character by character to produce tokens. • Normally a lexical analyzer doesn’t return a list of tokens at one shot, it returns a token when the parser asks a token from it. source program Lexical Analyzer token Parser get next token 19
Lexical Analyzer • Lexical Analyzer reads the source program character by character to produce tokens. • Normally a lexical analyzer doesn’t return a list of tokens at one shot, it returns a token when the parser asks a token from it. source program Lexical Analyzer token Parser get next token 19
 Token • Token represents a set of strings described by a pattern. – Identifier represents a set of strings which start with a letter continues with letters and digits – The actual string (newval) is called as lexeme. – Tokens: identifier, number, addop, delimeter, … • Since a token can represent more than one lexeme, additional information should be held for that specific lexeme. This additional information is called as the attribute of the token. • For simplicity, a token may have a single attribute which holds the required information for that token. – For identifiers, this attribute a pointer to the symbol table, and the symbol table holds the actual attributes for that token. • Some attributes: –
Token • Token represents a set of strings described by a pattern. – Identifier represents a set of strings which start with a letter continues with letters and digits – The actual string (newval) is called as lexeme. – Tokens: identifier, number, addop, delimeter, … • Since a token can represent more than one lexeme, additional information should be held for that specific lexeme. This additional information is called as the attribute of the token. • For simplicity, a token may have a single attribute which holds the required information for that token. – For identifiers, this attribute a pointer to the symbol table, and the symbol table holds the actual attributes for that token. • Some attributes: –
 Terminology of Languages • Alphabet : a finite set of symbols (ASCII characters) • String : – – Finite sequence of symbols on an alphabet Sentence and word are also used in terms of string is the empty string |s| is the length of string s. • Language: sets of strings over some fixed alphabet – – the empty set is a language. { } the set containing empty string is a language The set of well-formed C programs is a language The set of all possible identifiers is a language. • Operators on Strings: – Concatenation: xy represents the concatenation of strings x and y. s = s – sn = s s s. . s ( n times) s 0 = s=s 21
Terminology of Languages • Alphabet : a finite set of symbols (ASCII characters) • String : – – Finite sequence of symbols on an alphabet Sentence and word are also used in terms of string is the empty string |s| is the length of string s. • Language: sets of strings over some fixed alphabet – – the empty set is a language. { } the set containing empty string is a language The set of well-formed C programs is a language The set of all possible identifiers is a language. • Operators on Strings: – Concatenation: xy represents the concatenation of strings x and y. s = s – sn = s s s. . s ( n times) s 0 = s=s 21
 Operations on Languages • Concatenation: – L 1 L 2 = { s 1 s 2 | s 1 L 1 and s 2 L 2 } • Union – L 1 L 2 = { s | s L 1 or s L 2 } • Exponentiation: – L 0 = { } L 1 = L L 2 = LL • Kleene Closure – L* = • Positive Closure – L+ = 22
Operations on Languages • Concatenation: – L 1 L 2 = { s 1 s 2 | s 1 L 1 and s 2 L 2 } • Union – L 1 L 2 = { s | s L 1 or s L 2 } • Exponentiation: – L 0 = { } L 1 = L L 2 = LL • Kleene Closure – L* = • Positive Closure – L+ = 22
 Example • L 1 = {a, b, c, d} L 2 = {1, 2} • L 1 L 2 = {a 1, a 2, b 1, b 2, c 1, c 2, d 1, d 2} • L 1 L 2 = {a, b, c, d, 1, 2} • L 13 = all strings with length three (using a, b, c, d} • L 1* = all strings using letters a, b, c, d and empty string • L 1+ = doesn’t include the empty string 23
Example • L 1 = {a, b, c, d} L 2 = {1, 2} • L 1 L 2 = {a 1, a 2, b 1, b 2, c 1, c 2, d 1, d 2} • L 1 L 2 = {a, b, c, d, 1, 2} • L 13 = all strings with length three (using a, b, c, d} • L 1* = all strings using letters a, b, c, d and empty string • L 1+ = doesn’t include the empty string 23
 Regular Expressions • We use regular expressions to describe tokens of a programming language. • A regular expression is built up of simpler regular expressions (using defining rules) • Each regular expression denotes a language. • A language denoted by a regular expression is called as a regular set. 24
Regular Expressions • We use regular expressions to describe tokens of a programming language. • A regular expression is built up of simpler regular expressions (using defining rules) • Each regular expression denotes a language. • A language denoted by a regular expression is called as a regular set. 24
 Regular Expressions (Rules) Regular expressions over alphabet Reg. Expr a (r 1) | (r 2) (r 1) (r 2) (r)* (r) Language it denotes { } {a} L(r 1) L(r 2) L(r 1) L(r 2) (L(r))* L(r) • (r)+ = (r)(r)* • (r)* = (r)* | 25
Regular Expressions (Rules) Regular expressions over alphabet Reg. Expr a (r 1) | (r 2) (r 1) (r 2) (r)* (r) Language it denotes { } {a} L(r 1) L(r 2) L(r 1) L(r 2) (L(r))* L(r) • (r)+ = (r)(r)* • (r)* = (r)* | 25
 Regular Expressions (cont. ) • We may remove parentheses by using precedence rules. – * – concatenation – | • ab*|c means highest next lowest (a(b)*)|(c) • Ex: – – – = {0, 1} 0|1 => {0, 1} (0|1) => {00, 01, 10, 11} 0* => { , 0, 000, 0000, . . } (0|1)* => all strings with 0 and 1, including the empty string 26
Regular Expressions (cont. ) • We may remove parentheses by using precedence rules. – * – concatenation – | • ab*|c means highest next lowest (a(b)*)|(c) • Ex: – – – = {0, 1} 0|1 => {0, 1} (0|1) => {00, 01, 10, 11} 0* => { , 0, 000, 0000, . . } (0|1)* => all strings with 0 and 1, including the empty string 26
 Regular Definitions • To write regular expression for some languages can be difficult, because their regular expressions can be quite complex. In those cases, we may use regular definitions. • We can give names to regular expressions, and we can use these names as symbols to define other regular expressions. • A regular definition is a sequence of the definitions of the form: d 1 r 1 where di is a distinct name and d 2 r 2 ri is a regular expression over symbols in. {d 1, d 2, . . . , di-1} dn rn basic symbols previously defined names 27
Regular Definitions • To write regular expression for some languages can be difficult, because their regular expressions can be quite complex. In those cases, we may use regular definitions. • We can give names to regular expressions, and we can use these names as symbols to define other regular expressions. • A regular definition is a sequence of the definitions of the form: d 1 r 1 where di is a distinct name and d 2 r 2 ri is a regular expression over symbols in. {d 1, d 2, . . . , di-1} dn rn basic symbols previously defined names 27
 Regular Definitions (cont. ) • Ex: Identifiers in Pascal letter A | B |. . . | Z | a | b |. . . | z digit 0 | 1 |. . . | 9 id letter (letter | digit ) * – If we try to write the regular expression representing identifiers without using regular definitions, that regular expression will be complex. (A|. . . |Z|a|. . . |z) ( (A|. . . |Z|a|. . . |z) | (0|. . . |9) ) * • Ex: Unsigned numbers in Pascal digit 0 | 1 |. . . | 9 digits digit + opt-fraction (. digits ) ? opt-exponent ( E (+|-)? digits ) ? unsigned-num digits opt-fraction opt-exponent 28
Regular Definitions (cont. ) • Ex: Identifiers in Pascal letter A | B |. . . | Z | a | b |. . . | z digit 0 | 1 |. . . | 9 id letter (letter | digit ) * – If we try to write the regular expression representing identifiers without using regular definitions, that regular expression will be complex. (A|. . . |Z|a|. . . |z) ( (A|. . . |Z|a|. . . |z) | (0|. . . |9) ) * • Ex: Unsigned numbers in Pascal digit 0 | 1 |. . . | 9 digits digit + opt-fraction (. digits ) ? opt-exponent ( E (+|-)? digits ) ? unsigned-num digits opt-fraction opt-exponent 28
 Finite Automata • A recognizer for a language is a program that takes a string x, and answers “yes” if x is a sentence of that language, and “no” otherwise. • We call the recognizer of the tokens as a finite automaton. • A finite automaton can be: deterministic(DFA) or non-deterministic (NFA) • This means that we may use a deterministic or non-deterministic automaton as a lexical analyzer. • Both deterministic and non-deterministic finite automaton recognize regular sets. • Which one? – deterministic – faster recognizer, but it may take more space – non-deterministic – slower, but it may take less space – Deterministic automatons are widely used lexical analyzers. • First, we define regular expressions for tokens; Then we convert them into a DFA to get a lexical analyzer for our tokens. – Algorithm 1: Regular Expression NFA DFA (two steps: first to NFA, then to DFA) – Algorithm 2: Regular Expression DFA (directly convert a regular expression into a DFA) 29
Finite Automata • A recognizer for a language is a program that takes a string x, and answers “yes” if x is a sentence of that language, and “no” otherwise. • We call the recognizer of the tokens as a finite automaton. • A finite automaton can be: deterministic(DFA) or non-deterministic (NFA) • This means that we may use a deterministic or non-deterministic automaton as a lexical analyzer. • Both deterministic and non-deterministic finite automaton recognize regular sets. • Which one? – deterministic – faster recognizer, but it may take more space – non-deterministic – slower, but it may take less space – Deterministic automatons are widely used lexical analyzers. • First, we define regular expressions for tokens; Then we convert them into a DFA to get a lexical analyzer for our tokens. – Algorithm 1: Regular Expression NFA DFA (two steps: first to NFA, then to DFA) – Algorithm 2: Regular Expression DFA (directly convert a regular expression into a DFA) 29
 Non-Deterministic Finite Automaton (NFA) • A non-deterministic finite automaton (NFA) is a mathematical model that consists of: – – – S - a set of states - a set of input symbols (alphabet) move – a transition function move to map state-symbol pairs to sets of states. s 0 - a start (initial) state F – a set of accepting states (final states) • - transitions are allowed in NFAs. In other words, we can move from one state to another one without consuming any symbol. • A NFA accepts a string x, if and only if there is a path from the starting state to one of accepting states such that edge labels along this path spell out x. 30
Non-Deterministic Finite Automaton (NFA) • A non-deterministic finite automaton (NFA) is a mathematical model that consists of: – – – S - a set of states - a set of input symbols (alphabet) move – a transition function move to map state-symbol pairs to sets of states. s 0 - a start (initial) state F – a set of accepting states (final states) • - transitions are allowed in NFAs. In other words, we can move from one state to another one without consuming any symbol. • A NFA accepts a string x, if and only if there is a path from the starting state to one of accepting states such that edge labels along this path spell out x. 30
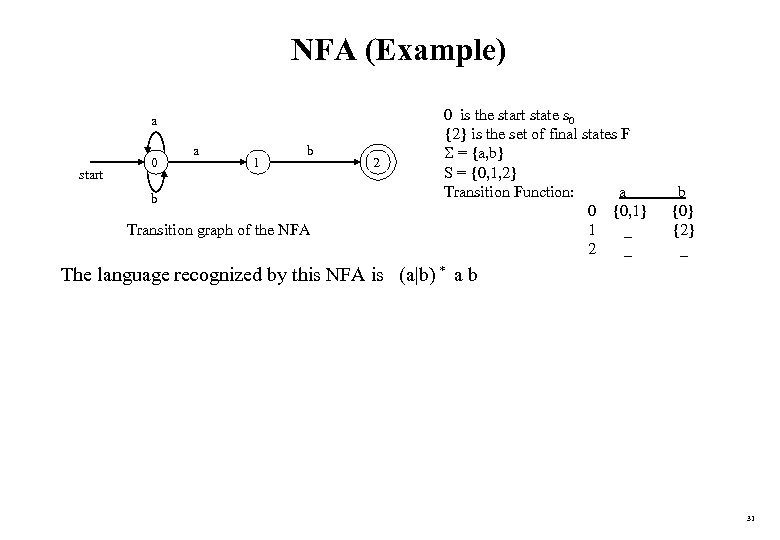 NFA (Example) a start 0 a 1 b b Transition graph of the NFA 2 0 is the start state s 0 {2} is the set of final states F = {a, b} S = {0, 1, 2} Transition Function: a 0 {0, 1} 1 _ 2 _ b {0} {2} _ The language recognized by this NFA is (a|b) * a b 31
NFA (Example) a start 0 a 1 b b Transition graph of the NFA 2 0 is the start state s 0 {2} is the set of final states F = {a, b} S = {0, 1, 2} Transition Function: a 0 {0, 1} 1 _ 2 _ b {0} {2} _ The language recognized by this NFA is (a|b) * a b 31
 Deterministic Finite Automaton (DFA) • A Deterministic Finite Automaton (DFA) is a special form of a NFA. • no state has - transition • for each symbol a and state s, there is at most one labeled edge a leaving s. i. e. transition function is from pair of state-symbol to state (not set of states) b 0 a a a 1 b The language recognized by 2 this DFA is also (a|b) * a b b 32
Deterministic Finite Automaton (DFA) • A Deterministic Finite Automaton (DFA) is a special form of a NFA. • no state has - transition • for each symbol a and state s, there is at most one labeled edge a leaving s. i. e. transition function is from pair of state-symbol to state (not set of states) b 0 a a a 1 b The language recognized by 2 this DFA is also (a|b) * a b b 32
 Implementing a DFA • Le us assume that the end of a string is marked with a special symbol (say eos). The algorithm for recognition will be as follows: (an efficient implementation) s s 0 c nextchar while (c != eos) do begin s move(s, c) c nextchar end if (s in F) then return “yes” else return “no” { start from the initial state } { get the next character from the input string } { do until the end of the string } { transition function } { if s is an accepting state } 33
Implementing a DFA • Le us assume that the end of a string is marked with a special symbol (say eos). The algorithm for recognition will be as follows: (an efficient implementation) s s 0 c nextchar while (c != eos) do begin s move(s, c) c nextchar end if (s in F) then return “yes” else return “no” { start from the initial state } { get the next character from the input string } { do until the end of the string } { transition function } { if s is an accepting state } 33
 Implementing a NFA S -closure({s 0}) { set all of states can be accessible from s 0 by -transitions } c nextchar while (c != eos) { begin s -closure(move(S, c)) { set of all states can be accessible from a state in S c nextchar by a transition on c } end if (S F != ) then return “yes” else return “no” • { if S contains an accepting state } This algorithm is not efficient. 34
Implementing a NFA S -closure({s 0}) { set all of states can be accessible from s 0 by -transitions } c nextchar while (c != eos) { begin s -closure(move(S, c)) { set of all states can be accessible from a state in S c nextchar by a transition on c } end if (S F != ) then return “yes” else return “no” • { if S contains an accepting state } This algorithm is not efficient. 34
 Converting A Regular Expression into A NFA (Thomson’s Construction) • This is one way to convert a regular expression into a NFA. • There can be other ways (much efficient) for the conversion. • Thomson’s Construction is simple and systematic method. It guarantees that the resulting NFA will have exactly one final state, and one start state. • Construction starts from simplest parts (alphabet symbols). To create a NFA for a complex regular expression, NFAs of its sub -expressions are combined to create its NFA, 35
Converting A Regular Expression into A NFA (Thomson’s Construction) • This is one way to convert a regular expression into a NFA. • There can be other ways (much efficient) for the conversion. • Thomson’s Construction is simple and systematic method. It guarantees that the resulting NFA will have exactly one final state, and one start state. • Construction starts from simplest parts (alphabet symbols). To create a NFA for a complex regular expression, NFAs of its sub -expressions are combined to create its NFA, 35
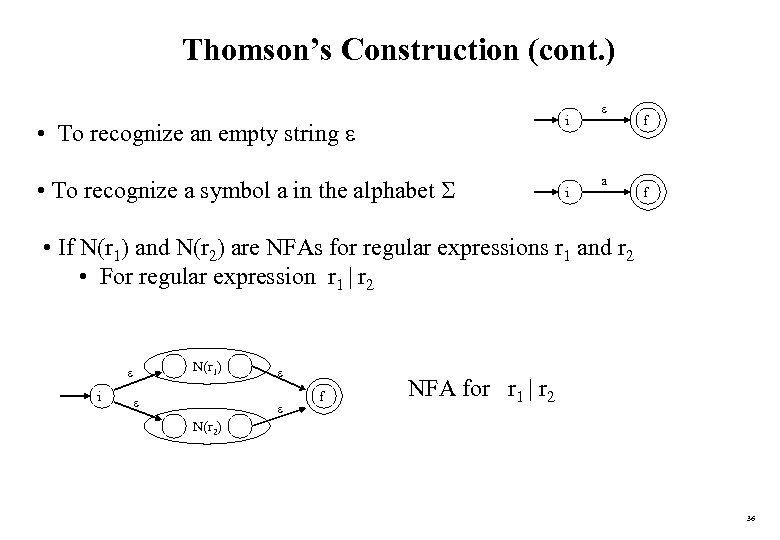 Thomson’s Construction (cont. ) i • To recognize an empty string • To recognize a symbol a in the alphabet i a f f • If N(r 1) and N(r 2) are NFAs for regular expressions r 1 and r 2 • For regular expression r 1 | r 2 i N(r 1) f NFA for r 1 | r 2 N(r 2) 36
Thomson’s Construction (cont. ) i • To recognize an empty string • To recognize a symbol a in the alphabet i a f f • If N(r 1) and N(r 2) are NFAs for regular expressions r 1 and r 2 • For regular expression r 1 | r 2 i N(r 1) f NFA for r 1 | r 2 N(r 2) 36
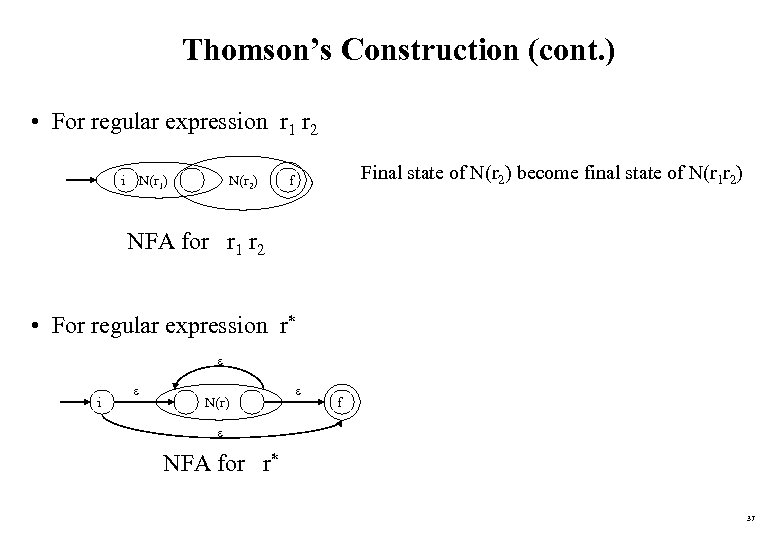 Thomson’s Construction (cont. ) • For regular expression r 1 r 2 i N(r 1) N(r 2) Final state of N(r 2) become final state of N(r 1 r 2) f NFA for r 1 r 2 • For regular expression r* i N(r) f NFA for r* 37
Thomson’s Construction (cont. ) • For regular expression r 1 r 2 i N(r 1) N(r 2) Final state of N(r 2) become final state of N(r 1 r 2) f NFA for r 1 r 2 • For regular expression r* i N(r) f NFA for r* 37
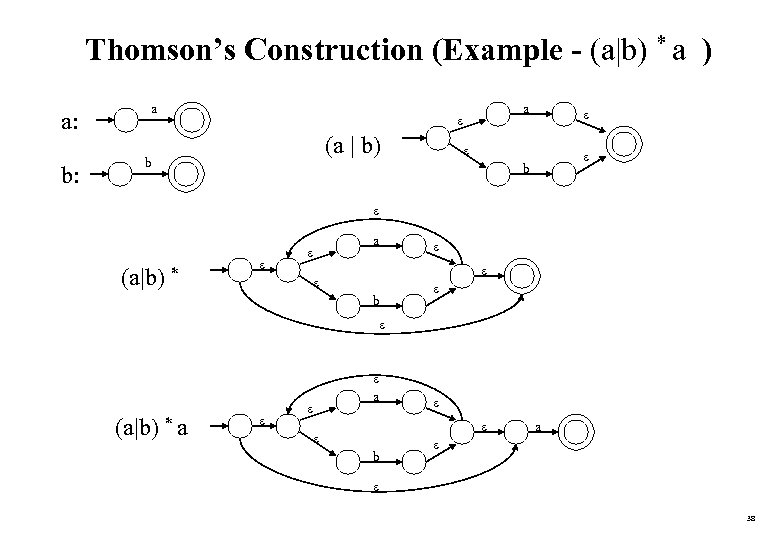 Thomson’s Construction (Example - (a|b) * a ) a: b: a a (a | b) b b (a|b) * a b (a|b) * a b a 38
Thomson’s Construction (Example - (a|b) * a ) a: b: a a (a | b) b b (a|b) * a b (a|b) * a b a 38
 Converting a NFA into a DFA (subset construction) put -closure({s 0}) as an unmarked state into the set of DFA (DS) while (there is one unmarked S 1 in DS) do -closure({s 0}) is the set of all states can be accessible begin from s 0 by -transition. mark S 1 set of states to which there is a transition on for each input symbol a do a from a state s in S 1 begin S 2 -closure(move(S 1, a)) if (S 2 is not in DS) then add S 2 into DS as an unmarked state transfunc[S 1, a] S 2 end • a state S in DS is an accepting state of DFA if a state in S is an accepting state of NFA • the start state of DFA is -closure({s 0}) 39
Converting a NFA into a DFA (subset construction) put -closure({s 0}) as an unmarked state into the set of DFA (DS) while (there is one unmarked S 1 in DS) do -closure({s 0}) is the set of all states can be accessible begin from s 0 by -transition. mark S 1 set of states to which there is a transition on for each input symbol a do a from a state s in S 1 begin S 2 -closure(move(S 1, a)) if (S 2 is not in DS) then add S 2 into DS as an unmarked state transfunc[S 1, a] S 2 end • a state S in DS is an accepting state of DFA if a state in S is an accepting state of NFA • the start state of DFA is -closure({s 0}) 39
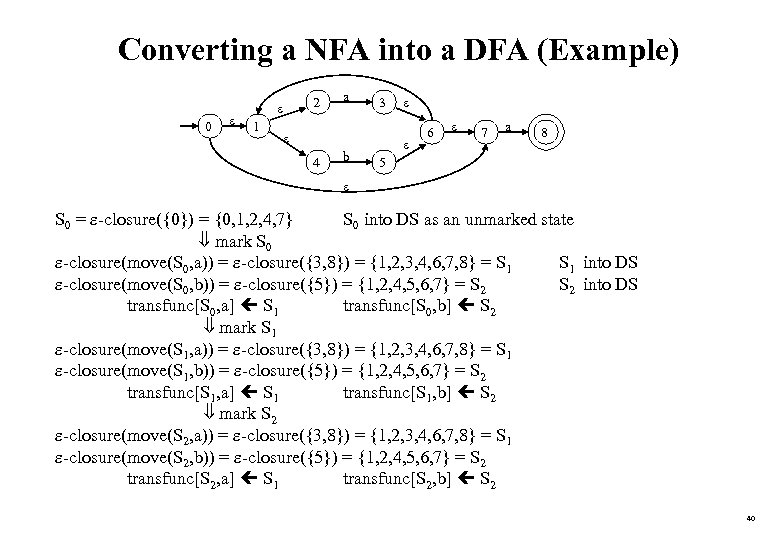 Converting a NFA into a DFA (Example) 0 1 2 a 3 4 b 6 7 a 8 5 S 0 = -closure({0}) = {0, 1, 2, 4, 7} S 0 into DS as an unmarked state mark S 0 -closure(move(S 0, a)) = -closure({3, 8}) = {1, 2, 3, 4, 6, 7, 8} = S 1 into DS -closure(move(S 0, b)) = -closure({5}) = {1, 2, 4, 5, 6, 7} = S 2 into DS transfunc[S 0, a] S 1 transfunc[S 0, b] S 2 mark S 1 -closure(move(S 1, a)) = -closure({3, 8}) = {1, 2, 3, 4, 6, 7, 8} = S 1 -closure(move(S 1, b)) = -closure({5}) = {1, 2, 4, 5, 6, 7} = S 2 transfunc[S 1, a] S 1 transfunc[S 1, b] S 2 mark S 2 -closure(move(S 2, a)) = -closure({3, 8}) = {1, 2, 3, 4, 6, 7, 8} = S 1 -closure(move(S 2, b)) = -closure({5}) = {1, 2, 4, 5, 6, 7} = S 2 transfunc[S 2, a] S 1 transfunc[S 2, b] S 2 40
Converting a NFA into a DFA (Example) 0 1 2 a 3 4 b 6 7 a 8 5 S 0 = -closure({0}) = {0, 1, 2, 4, 7} S 0 into DS as an unmarked state mark S 0 -closure(move(S 0, a)) = -closure({3, 8}) = {1, 2, 3, 4, 6, 7, 8} = S 1 into DS -closure(move(S 0, b)) = -closure({5}) = {1, 2, 4, 5, 6, 7} = S 2 into DS transfunc[S 0, a] S 1 transfunc[S 0, b] S 2 mark S 1 -closure(move(S 1, a)) = -closure({3, 8}) = {1, 2, 3, 4, 6, 7, 8} = S 1 -closure(move(S 1, b)) = -closure({5}) = {1, 2, 4, 5, 6, 7} = S 2 transfunc[S 1, a] S 1 transfunc[S 1, b] S 2 mark S 2 -closure(move(S 2, a)) = -closure({3, 8}) = {1, 2, 3, 4, 6, 7, 8} = S 1 -closure(move(S 2, b)) = -closure({5}) = {1, 2, 4, 5, 6, 7} = S 2 transfunc[S 2, a] S 1 transfunc[S 2, b] S 2 40
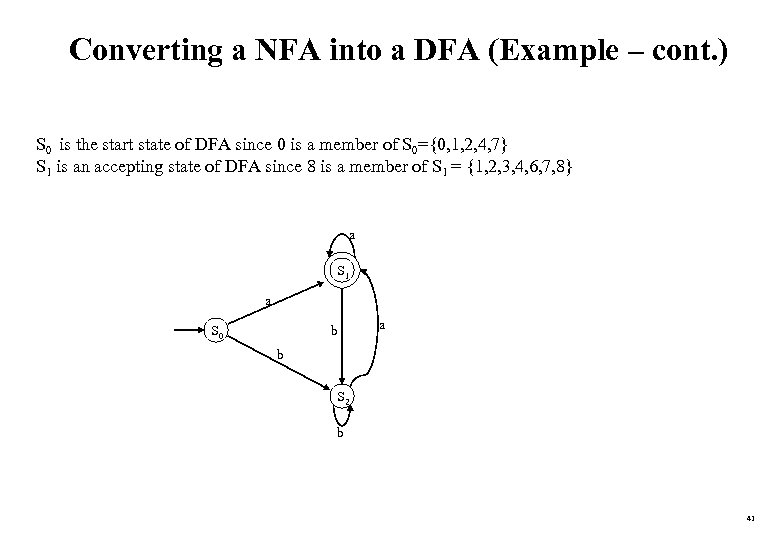 Converting a NFA into a DFA (Example – cont. ) S 0 is the start state of DFA since 0 is a member of S 0={0, 1, 2, 4, 7} S 1 is an accepting state of DFA since 8 is a member of S 1 = {1, 2, 3, 4, 6, 7, 8} a S 1 a S 0 b a b S 2 b 41
Converting a NFA into a DFA (Example – cont. ) S 0 is the start state of DFA since 0 is a member of S 0={0, 1, 2, 4, 7} S 1 is an accepting state of DFA since 8 is a member of S 1 = {1, 2, 3, 4, 6, 7, 8} a S 1 a S 0 b a b S 2 b 41
 Converting Regular Expressions Directly to DFAs • We may convert a regular expression into a DFA (without creating a NFA first). • First we augment the given regular expression by concatenating it with a special symbol #. r (r)# augmented regular expression • Then, we create a syntax tree for this augmented regular expression. • In this syntax tree, all alphabet symbols (plus # and the empty string) in the augmented regular expression will be on the leaves, and all inner nodes will be the operators in that augmented regular expression. • Then each alphabet symbol (plus #) will be numbered (position numbers). 42
Converting Regular Expressions Directly to DFAs • We may convert a regular expression into a DFA (without creating a NFA first). • First we augment the given regular expression by concatenating it with a special symbol #. r (r)# augmented regular expression • Then, we create a syntax tree for this augmented regular expression. • In this syntax tree, all alphabet symbols (plus # and the empty string) in the augmented regular expression will be on the leaves, and all inner nodes will be the operators in that augmented regular expression. • Then each alphabet symbol (plus #) will be numbered (position numbers). 42
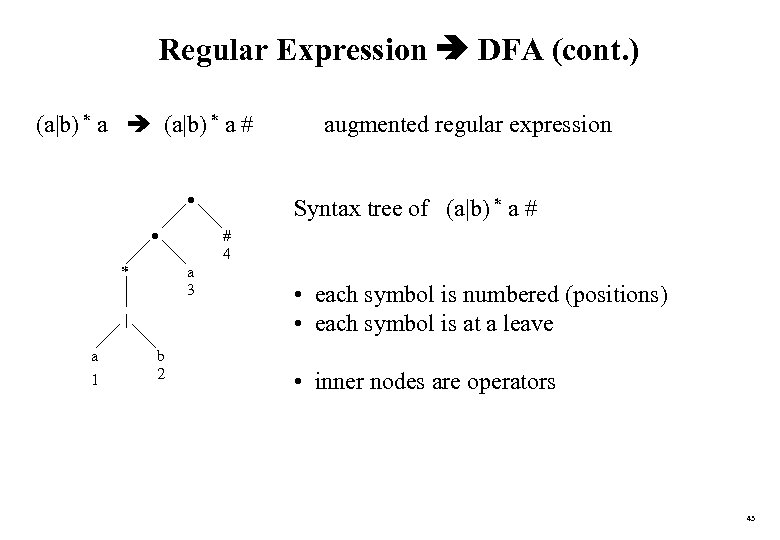 Regular Expression DFA (cont. ) (a|b) * a # * a 1 b 2 Syntax tree of (a|b) * a # # 4 a 3 | augmented regular expression • each symbol is numbered (positions) • each symbol is at a leave • inner nodes are operators 43
Regular Expression DFA (cont. ) (a|b) * a # * a 1 b 2 Syntax tree of (a|b) * a # # 4 a 3 | augmented regular expression • each symbol is numbered (positions) • each symbol is at a leave • inner nodes are operators 43
 followpos Then we define the function followpos for the positions (positions assigned to leaves). followpos(i) -- is the set of positions which can follow the position i in the strings generated by the augmented regular expression. For example, ( a | b) * a # 1 2 3 4 followpos(1) = {1, 2, 3} followpos(2) = {1, 2, 3} followpos(3) = {4} followpos(4) = {} followpos is just defined for leaves, it is not defined for inner nodes. 44
followpos Then we define the function followpos for the positions (positions assigned to leaves). followpos(i) -- is the set of positions which can follow the position i in the strings generated by the augmented regular expression. For example, ( a | b) * a # 1 2 3 4 followpos(1) = {1, 2, 3} followpos(2) = {1, 2, 3} followpos(3) = {4} followpos(4) = {} followpos is just defined for leaves, it is not defined for inner nodes. 44
 firstpos, lastpos, nullable • To evaluate followpos, we need three more functions to be defined for the nodes (not just for leaves) of the syntax tree. • firstpos(n) -- the set of the positions of the first symbols of strings generated by the sub-expression rooted by n. • lastpos(n) -- the set of the positions of the last symbols of strings generated by the sub-expression rooted by n. • nullable(n) -- true if the empty string is a member of strings generated by the sub-expression rooted by n false otherwise 45
firstpos, lastpos, nullable • To evaluate followpos, we need three more functions to be defined for the nodes (not just for leaves) of the syntax tree. • firstpos(n) -- the set of the positions of the first symbols of strings generated by the sub-expression rooted by n. • lastpos(n) -- the set of the positions of the last symbols of strings generated by the sub-expression rooted by n. • nullable(n) -- true if the empty string is a member of strings generated by the sub-expression rooted by n false otherwise 45
 How to evaluate firstpos, lastpos, nullable n nullable(n) firstpos(n) lastpos(n) leaf labeled true leaf labeled with position i false {i} firstpos(c 1) firstpos(c 2) lastpos(c 1) lastpos(c 2) c 2 nullable(c 1) or nullable(c 2) c 2 nullable(c 1) and nullable(c 2) if (nullable(c 1)) firstpos(c 1) firstpos(c 2) else firstpos(c 1) if (nullable(c 2)) lastpos(c 1) lastpos(c 2) else lastpos(c 2) firstpos(c 1) lastpos(c 1) | c 1 * c 1 true 46
How to evaluate firstpos, lastpos, nullable n nullable(n) firstpos(n) lastpos(n) leaf labeled true leaf labeled with position i false {i} firstpos(c 1) firstpos(c 2) lastpos(c 1) lastpos(c 2) c 2 nullable(c 1) or nullable(c 2) c 2 nullable(c 1) and nullable(c 2) if (nullable(c 1)) firstpos(c 1) firstpos(c 2) else firstpos(c 1) if (nullable(c 2)) lastpos(c 1) lastpos(c 2) else lastpos(c 2) firstpos(c 1) lastpos(c 1) | c 1 * c 1 true 46
 How to evaluate followpos • Two-rules define the function followpos: 1. If n is concatenation-node with left child c 1 and right child c 2, and i is a position in lastpos(c 1), then all positions in firstpos(c 2) are in followpos(i). 2. If n is a star-node, and i is a position in lastpos(n), then all positions in firstpos(n) are in followpos(i). • If firstpos and lastpos have been computed for each node, followpos of each position can be computed by making one depth-first traversal of the syntax tree. 47
How to evaluate followpos • Two-rules define the function followpos: 1. If n is concatenation-node with left child c 1 and right child c 2, and i is a position in lastpos(c 1), then all positions in firstpos(c 2) are in followpos(i). 2. If n is a star-node, and i is a position in lastpos(n), then all positions in firstpos(n) are in followpos(i). • If firstpos and lastpos have been computed for each node, followpos of each position can be computed by making one depth-first traversal of the syntax tree. 47
 Example -- ( a | b) * a # {1, 2, 3} {4} {1, 2, 3} {3} {4} # {4} 4 {1, 2} *{1, 2} {3} a{3} 3 {1, 2} | {1, 2} {1} a {1} {2} b {2} 2 1 red – firstpos blue – lastpos Then we can calculate followpos(1) = {1, 2, 3} followpos(2) = {1, 2, 3} followpos(3) = {4} followpos(4) = {} • After we calculate follow positions, we are ready to create DFA for the regular expression. 48
Example -- ( a | b) * a # {1, 2, 3} {4} {1, 2, 3} {3} {4} # {4} 4 {1, 2} *{1, 2} {3} a{3} 3 {1, 2} | {1, 2} {1} a {1} {2} b {2} 2 1 red – firstpos blue – lastpos Then we can calculate followpos(1) = {1, 2, 3} followpos(2) = {1, 2, 3} followpos(3) = {4} followpos(4) = {} • After we calculate follow positions, we are ready to create DFA for the regular expression. 48
 Algorithm (RE DFA) • • Create the syntax tree of (r) # Calculate the functions: followpos, firstpos, lastpos, nullable Put firstpos(root) into the states of DFA as an unmarked state. while (there is an unmarked state S in the states of DFA) do – mark S – for each input symbol a do • let s 1, . . . , sn are positions in S and symbols in those positions are a • S’ followpos(s 1) . . . followpos(sn) • move(S, a) S’ • if (S’ is not empty and not in the states of DFA) – put S’ into the states of DFA as an unmarked state. • the start state of DFA is firstpos(root) • the accepting states of DFA are all states containing the position of # 49
Algorithm (RE DFA) • • Create the syntax tree of (r) # Calculate the functions: followpos, firstpos, lastpos, nullable Put firstpos(root) into the states of DFA as an unmarked state. while (there is an unmarked state S in the states of DFA) do – mark S – for each input symbol a do • let s 1, . . . , sn are positions in S and symbols in those positions are a • S’ followpos(s 1) . . . followpos(sn) • move(S, a) S’ • if (S’ is not empty and not in the states of DFA) – put S’ into the states of DFA as an unmarked state. • the start state of DFA is firstpos(root) • the accepting states of DFA are all states containing the position of # 49
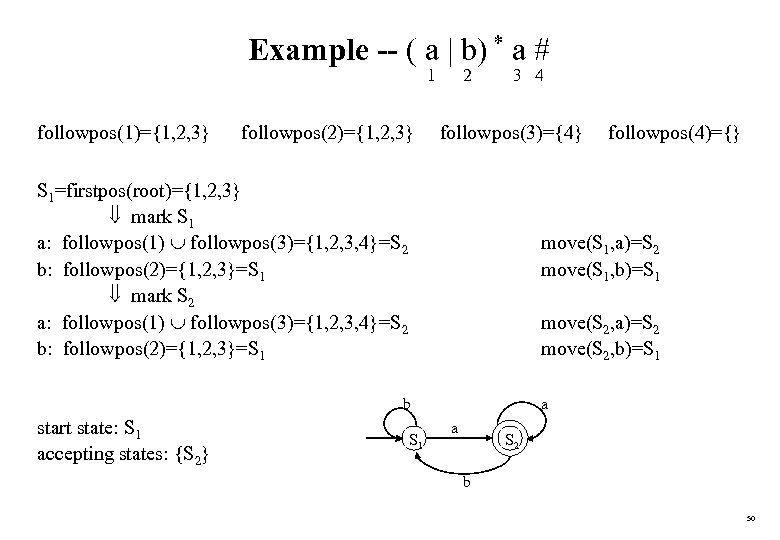 Example -- ( a | b) * a # 1 followpos(1)={1, 2, 3} followpos(2)={1, 2, 3} 2 3 4 followpos(3)={4} S 1=firstpos(root)={1, 2, 3} mark S 1 a: followpos(1) followpos(3)={1, 2, 3, 4}=S 2 b: followpos(2)={1, 2, 3}=S 1 mark S 2 a: followpos(1) followpos(3)={1, 2, 3, 4}=S 2 b: followpos(2)={1, 2, 3}=S 1 move(S 1, a)=S 2 move(S 1, b)=S 1 move(S 2, a)=S 2 move(S 2, b)=S 1 b start state: S 1 accepting states: {S 2} followpos(4)={} S 1 a a S 2 b 50
Example -- ( a | b) * a # 1 followpos(1)={1, 2, 3} followpos(2)={1, 2, 3} 2 3 4 followpos(3)={4} S 1=firstpos(root)={1, 2, 3} mark S 1 a: followpos(1) followpos(3)={1, 2, 3, 4}=S 2 b: followpos(2)={1, 2, 3}=S 1 mark S 2 a: followpos(1) followpos(3)={1, 2, 3, 4}=S 2 b: followpos(2)={1, 2, 3}=S 1 move(S 1, a)=S 2 move(S 1, b)=S 1 move(S 2, a)=S 2 move(S 2, b)=S 1 b start state: S 1 accepting states: {S 2} followpos(4)={} S 1 a a S 2 b 50
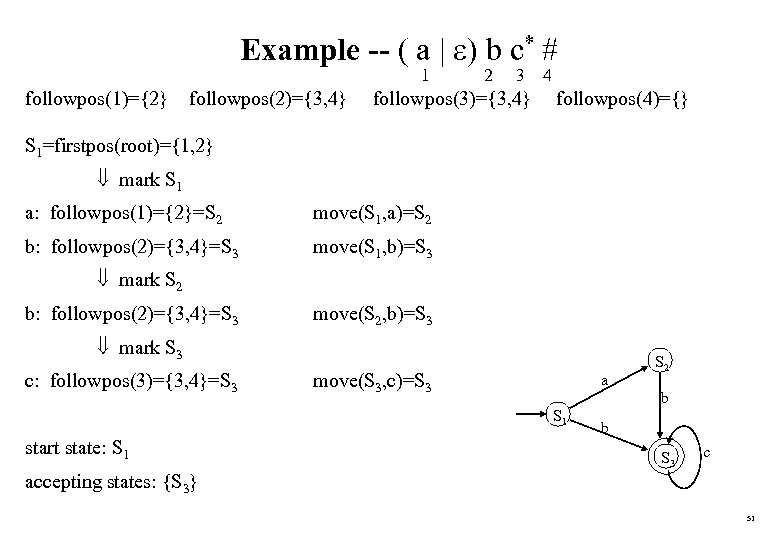 Example -- ( a | ) b c* # 1 followpos(1)={2} followpos(2)={3, 4} 2 3 4 followpos(3)={3, 4} followpos(4)={} S 1=firstpos(root)={1, 2} mark S 1 a: followpos(1)={2}=S 2 move(S 1, a)=S 2 b: followpos(2)={3, 4}=S 3 move(S 1, b)=S 3 mark S 2 b: followpos(2)={3, 4}=S 3 move(S 2, b)=S 3 mark S 3 c: followpos(3)={3, 4}=S 3 move(S 3, c)=S 3 a b S 1 start state: S 1 S 2 b S 3 c accepting states: {S 3} 51
Example -- ( a | ) b c* # 1 followpos(1)={2} followpos(2)={3, 4} 2 3 4 followpos(3)={3, 4} followpos(4)={} S 1=firstpos(root)={1, 2} mark S 1 a: followpos(1)={2}=S 2 move(S 1, a)=S 2 b: followpos(2)={3, 4}=S 3 move(S 1, b)=S 3 mark S 2 b: followpos(2)={3, 4}=S 3 move(S 2, b)=S 3 mark S 3 c: followpos(3)={3, 4}=S 3 move(S 3, c)=S 3 a b S 1 start state: S 1 S 2 b S 3 c accepting states: {S 3} 51
 Minimizing Number of States of a DFA • partition the set of states into two groups: – G 1 : set of accepting states – G 2 : set of non-accepting states • For each new group G – partition G into subgroups such that states s 1 and s 2 are in the same group iff for all input symbols a, states s 1 and s 2 have transitions to states in the same group. • Start state of the minimized DFA is the group containing the start state of the original DFA. • Accepting states of the minimized DFA are the groups containing the accepting states of the original DFA. 52
Minimizing Number of States of a DFA • partition the set of states into two groups: – G 1 : set of accepting states – G 2 : set of non-accepting states • For each new group G – partition G into subgroups such that states s 1 and s 2 are in the same group iff for all input symbols a, states s 1 and s 2 have transitions to states in the same group. • Start state of the minimized DFA is the group containing the start state of the original DFA. • Accepting states of the minimized DFA are the groups containing the accepting states of the original DFA. 52
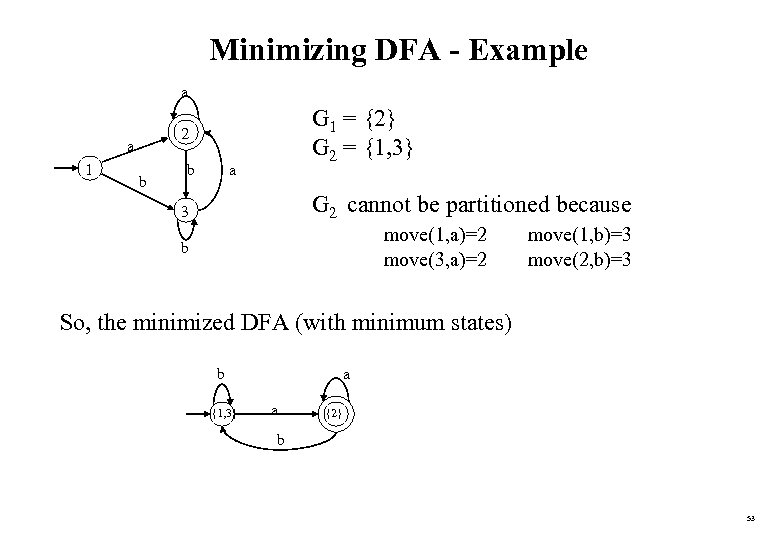 Minimizing DFA - Example a a 1 G 1 = {2} G 2 = {1, 3} 2 b b a G 2 cannot be partitioned because 3 move(1, a)=2 move(3, a)=2 b move(1, b)=3 move(2, b)=3 So, the minimized DFA (with minimum states) b {1, 3} a a {2} b 53
Minimizing DFA - Example a a 1 G 1 = {2} G 2 = {1, 3} 2 b b a G 2 cannot be partitioned because 3 move(1, a)=2 move(3, a)=2 b move(1, b)=3 move(2, b)=3 So, the minimized DFA (with minimum states) b {1, 3} a a {2} b 53
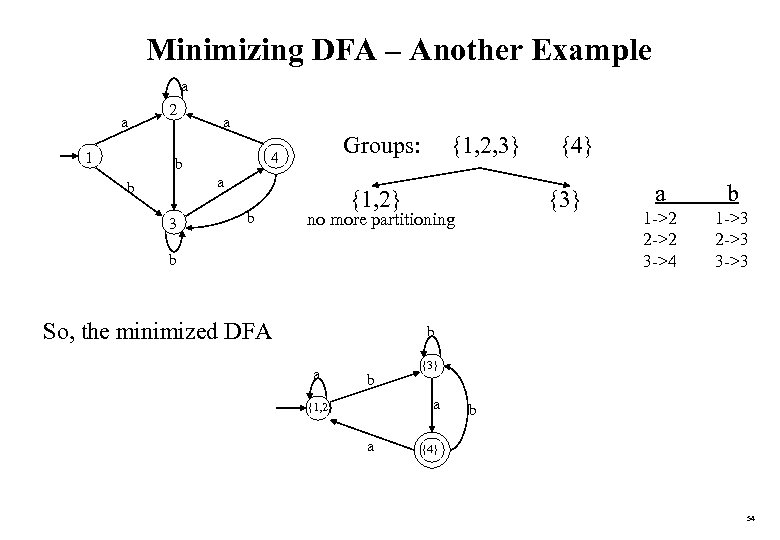 Minimizing DFA – Another Example a a 1 2 a Groups: 4 b a b 3 b {1, 2, 3} {1, 2} {3} no more partitioning b So, the minimized DFA {4} a b 1 ->2 2 ->2 3 ->4 1 ->3 2 ->3 3 ->3 b a b {3} a {1, 2} a b {4} 54
Minimizing DFA – Another Example a a 1 2 a Groups: 4 b a b 3 b {1, 2, 3} {1, 2} {3} no more partitioning b So, the minimized DFA {4} a b 1 ->2 2 ->2 3 ->4 1 ->3 2 ->3 3 ->3 b a b {3} a {1, 2} a b {4} 54
 Some Other Issues in Lexical Analyzer • The lexical analyzer has to recognize the longest possible string. – Ex: identifier newval -- n ne newval • What is the end of a token? Is there any character which marks the end of a token? – – – It is normally not defined. If the number of characters in a token is fixed, in that case no problem: + But < < or <> (in Pascal) The end of an identifier : the characters cannot be in an identifier can mark the end of token. We may need a lookhead • In Prolog: p : - X is 1. 5. The dot followed by a white space character can mark the end of a number. if that is not the case, the dot must be treated as a part of the number. But 55
Some Other Issues in Lexical Analyzer • The lexical analyzer has to recognize the longest possible string. – Ex: identifier newval -- n ne newval • What is the end of a token? Is there any character which marks the end of a token? – – – It is normally not defined. If the number of characters in a token is fixed, in that case no problem: + But < < or <> (in Pascal) The end of an identifier : the characters cannot be in an identifier can mark the end of token. We may need a lookhead • In Prolog: p : - X is 1. 5. The dot followed by a white space character can mark the end of a number. if that is not the case, the dot must be treated as a part of the number. But 55
 Some Other Issues in Lexical Analyzer (cont. ) • Skipping comments – Normally we don’t return a comment as a token. – We skip a comment, and return the next token (which is not a comment) to the parser. – So, the comments are only processed by the lexical analyzer, and the don’t complicate syntax of the language. the • Symbol table interface – symbol table holds information about tokens (at least lexeme of identifiers) – how to implement the symbol table, and what kind of operations. • hash table – open addressing, chaining • putting into the hash table, finding the position of a token from its lexeme. • Positions of the tokens in the file (for the error handling). 56
Some Other Issues in Lexical Analyzer (cont. ) • Skipping comments – Normally we don’t return a comment as a token. – We skip a comment, and return the next token (which is not a comment) to the parser. – So, the comments are only processed by the lexical analyzer, and the don’t complicate syntax of the language. the • Symbol table interface – symbol table holds information about tokens (at least lexeme of identifiers) – how to implement the symbol table, and what kind of operations. • hash table – open addressing, chaining • putting into the hash table, finding the position of a token from its lexeme. • Positions of the tokens in the file (for the error handling). 56
 Syntax Analyzer • • Syntax Analyzer creates the syntactic structure of the given source program. This syntactic structure is mostly a parse tree. Syntax Analyzer is also known as parser. The syntax of a programming is described by a context-free grammar (CFG). We will use BNF (Backus-Naur Form) notation in the description of CFGs. • The syntax analyzer (parser) checks whether a given source program satisfies the rules implied by a context-free grammar or not. – If it satisfies, the parser creates the parse tree of that program. – Otherwise the parser gives the error messages. • A context-free grammar – gives a precise syntactic specification of a programming language. – the design of the grammar is an initial phase of the design of a compiler. – a grammar can be directly converted into a parser by some tools. 57
Syntax Analyzer • • Syntax Analyzer creates the syntactic structure of the given source program. This syntactic structure is mostly a parse tree. Syntax Analyzer is also known as parser. The syntax of a programming is described by a context-free grammar (CFG). We will use BNF (Backus-Naur Form) notation in the description of CFGs. • The syntax analyzer (parser) checks whether a given source program satisfies the rules implied by a context-free grammar or not. – If it satisfies, the parser creates the parse tree of that program. – Otherwise the parser gives the error messages. • A context-free grammar – gives a precise syntactic specification of a programming language. – the design of the grammar is an initial phase of the design of a compiler. – a grammar can be directly converted into a parser by some tools. 57
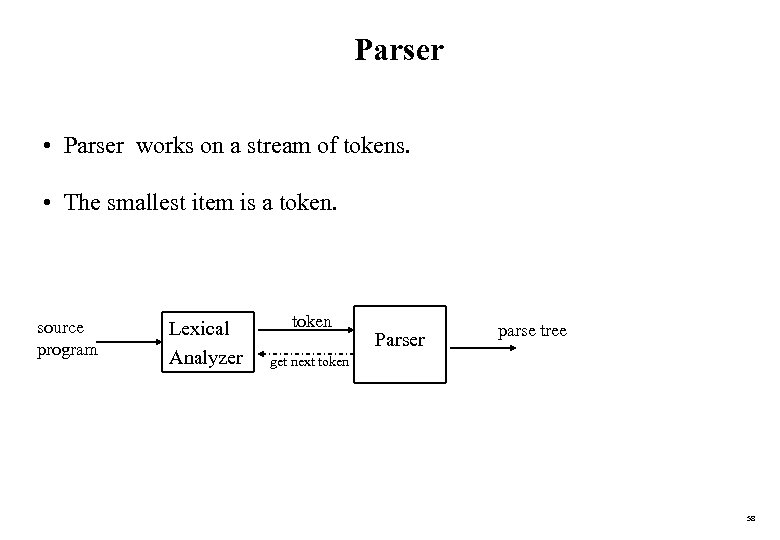 Parser • Parser works on a stream of tokens. • The smallest item is a token. source program Lexical Analyzer token Parser parse tree get next token 58
Parser • Parser works on a stream of tokens. • The smallest item is a token. source program Lexical Analyzer token Parser parse tree get next token 58
 Parsers (cont. ) • We categorize the parsers into two groups: 1. Top-Down Parser – The parse tree is created top to bottom, starting from the root. 2. Bottom-Up Parser – The parse is created bottom to top; starting from the leaves • • Both top-down and bottom-up parsers scan the input from left to right (one symbol at a time). Efficient top-down and bottom-up parsers can be implemented only for sub-classes of context-free grammars. – LL for top-down parsing – LR for bottom-up parsing 59
Parsers (cont. ) • We categorize the parsers into two groups: 1. Top-Down Parser – The parse tree is created top to bottom, starting from the root. 2. Bottom-Up Parser – The parse is created bottom to top; starting from the leaves • • Both top-down and bottom-up parsers scan the input from left to right (one symbol at a time). Efficient top-down and bottom-up parsers can be implemented only for sub-classes of context-free grammars. – LL for top-down parsing – LR for bottom-up parsing 59
 Context-Free Grammars • Inherently recursive structures of a programming language are defined by a context-free grammar. • In a context-free grammar, we have: – A finite set of terminals (in our case, this will be the set of tokens) – A finite set of non-terminals (syntactic-variables) – A finite set of productions rules in the following form • A where A is a non-terminal and is a string of terminals and non-terminals (including the empty string) – A start symbol (one of the non-terminal symbol) • Example: E E+E | E–E | E*E | E/E | -E E (E) E id 60
Context-Free Grammars • Inherently recursive structures of a programming language are defined by a context-free grammar. • In a context-free grammar, we have: – A finite set of terminals (in our case, this will be the set of tokens) – A finite set of non-terminals (syntactic-variables) – A finite set of productions rules in the following form • A where A is a non-terminal and is a string of terminals and non-terminals (including the empty string) – A start symbol (one of the non-terminal symbol) • Example: E E+E | E–E | E*E | E/E | -E E (E) E id 60
 Derivations E E+E • E+E derives from E – we can replace E by E+E – to able to do this, we have to have a production rule E E+E in our grammar. E E+E id+id • A sequence of replacements of non-terminal symbols is called a derivation of id+id from E. • In general a derivation step is A if there is a production rule A in our grammar where and are arbitrary strings of terminal and non-terminal symbols 1 2 . . . n * + ( n derives from 1 or 1 derives n ) : derives in one step : derives in zero or more steps : derives in one or more steps 61
Derivations E E+E • E+E derives from E – we can replace E by E+E – to able to do this, we have to have a production rule E E+E in our grammar. E E+E id+id • A sequence of replacements of non-terminal symbols is called a derivation of id+id from E. • In general a derivation step is A if there is a production rule A in our grammar where and are arbitrary strings of terminal and non-terminal symbols 1 2 . . . n * + ( n derives from 1 or 1 derives n ) : derives in one step : derives in zero or more steps : derives in one or more steps 61
 CFG - Terminology • L(G) is the language of G (the language generated by G) which is a set of sentences. • A sentence of L(G) is a string of terminal symbols of G. • If S is the start symbol of G then + is a sentence of L(G) iff S where is a string of terminals of G. • If G is a context-free grammar, L(G) is a context-free language. • Two grammars are equivalent if they produce the same language. * • S - If contains non-terminals, it is called as a sentential form of G. - If does not contain non-terminals, it is called as a sentence of G. 62
CFG - Terminology • L(G) is the language of G (the language generated by G) which is a set of sentences. • A sentence of L(G) is a string of terminal symbols of G. • If S is the start symbol of G then + is a sentence of L(G) iff S where is a string of terminals of G. • If G is a context-free grammar, L(G) is a context-free language. • Two grammars are equivalent if they produce the same language. * • S - If contains non-terminals, it is called as a sentential form of G. - If does not contain non-terminals, it is called as a sentence of G. 62
 Derivation Example E -(E) -(E+E) -(id+id) OR E -(E) -(E+id) -(id+id) • At each derivation step, we can choose any of the non-terminal in the sentential form of G for the replacement. • If we always choose the left-most non-terminal in each derivation step, this derivation is called as left-most derivation. • If we always choose the right-most non-terminal in each derivation step, this derivation is called as right-most derivation. 63
Derivation Example E -(E) -(E+E) -(id+id) OR E -(E) -(E+id) -(id+id) • At each derivation step, we can choose any of the non-terminal in the sentential form of G for the replacement. • If we always choose the left-most non-terminal in each derivation step, this derivation is called as left-most derivation. • If we always choose the right-most non-terminal in each derivation step, this derivation is called as right-most derivation. 63
 Left-Most and Right-Most Derivations Left-Most Derivation E -(E) lm -(E+E) lm -(id+E) -(id+id) lm lm lm Right-Most Derivation E -(E) rm -(E+id) -(id+id) rm rm rm • We will see that the top-down parsers try to find the left-most derivation of the given source program. • We will see that the bottom-up parsers try to find the right-most derivation of the given source program in the reverse order. 64
Left-Most and Right-Most Derivations Left-Most Derivation E -(E) lm -(E+E) lm -(id+E) -(id+id) lm lm lm Right-Most Derivation E -(E) rm -(E+id) -(id+id) rm rm rm • We will see that the top-down parsers try to find the left-most derivation of the given source program. • We will see that the bottom-up parsers try to find the right-most derivation of the given source program in the reverse order. 64
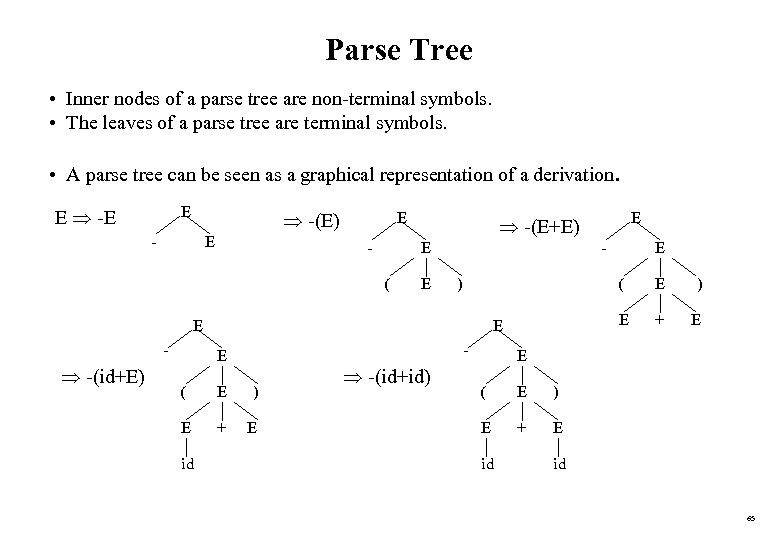 Parse Tree • Inner nodes of a parse tree are non-terminal symbols. • The leaves of a parse tree are terminal symbols. • A parse tree can be seen as a graphical representation of a derivation. E E -(E) - E E - E ( E ) -(id+E) - ( E ) E + E id -(id+id) E E E E ( E - E -(E+E) + E E ( E ) E + E id id 65
Parse Tree • Inner nodes of a parse tree are non-terminal symbols. • The leaves of a parse tree are terminal symbols. • A parse tree can be seen as a graphical representation of a derivation. E E -(E) - E E - E ( E ) -(id+E) - ( E ) E + E id -(id+id) E E E E ( E - E -(E+E) + E E ( E ) E + E id id 65
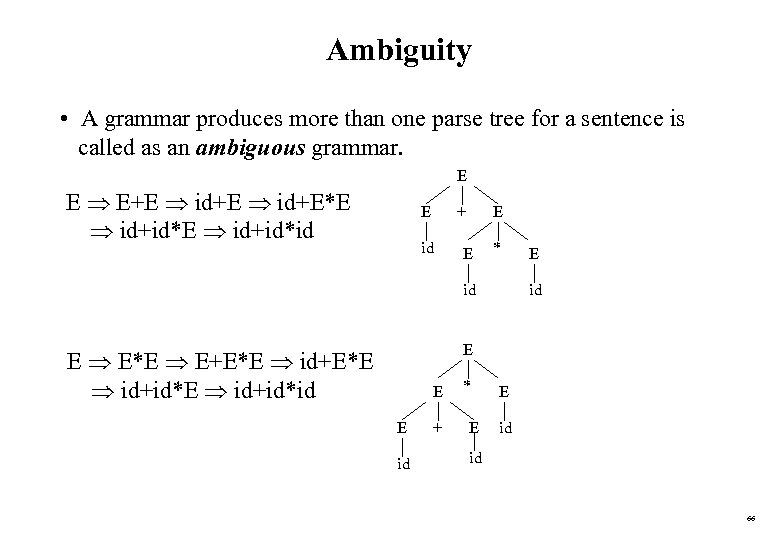 Ambiguity • A grammar produces more than one parse tree for a sentence is called as an ambiguous grammar. E E E+E id+E*E id+id*id E + id E E * id E E E*E E+E*E id+id*E id+id*id E E id + * E E id id 66
Ambiguity • A grammar produces more than one parse tree for a sentence is called as an ambiguous grammar. E E E+E id+E*E id+id*id E + id E E * id E E E*E E+E*E id+id*E id+id*id E E id + * E E id id 66
 Ambiguity (cont. ) • For the most parsers, the grammar must be unambiguous. • unambiguous grammar unique selection of the parse tree for a sentence • We should eliminate the ambiguity in the grammar during the design phase of the compiler. • An unambiguous grammar should be written to eliminate the ambiguity. • We have to prefer one of the parse trees of a sentence (generated by an ambiguous grammar) to disambiguate that grammar to restrict to this choice. 67
Ambiguity (cont. ) • For the most parsers, the grammar must be unambiguous. • unambiguous grammar unique selection of the parse tree for a sentence • We should eliminate the ambiguity in the grammar during the design phase of the compiler. • An unambiguous grammar should be written to eliminate the ambiguity. • We have to prefer one of the parse trees of a sentence (generated by an ambiguous grammar) to disambiguate that grammar to restrict to this choice. 67
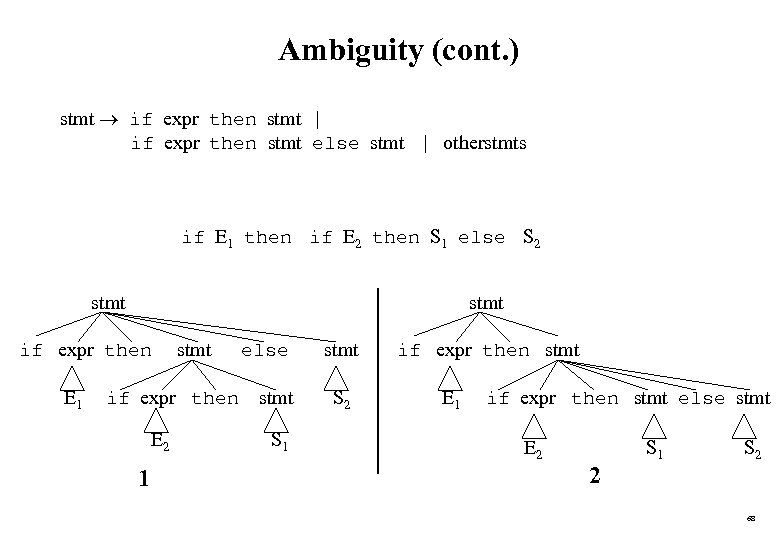 Ambiguity (cont. ) stmt if expr then stmt | if expr then stmt else stmt | otherstmts if E 1 then if E 2 then S 1 else S 2 stmt if expr then E 1 stmt if expr then E 2 1 else stmt S 1 stmt S 2 if expr then stmt E 1 if expr then stmt else stmt E 2 2 S 1 S 2 68
Ambiguity (cont. ) stmt if expr then stmt | if expr then stmt else stmt | otherstmts if E 1 then if E 2 then S 1 else S 2 stmt if expr then E 1 stmt if expr then E 2 1 else stmt S 1 stmt S 2 if expr then stmt E 1 if expr then stmt else stmt E 2 2 S 1 S 2 68
 Ambiguity (cont. ) • We prefer the second parse tree (else matches with closest if). • So, we have to disambiguate our grammar to reflect this choice. • The unambiguous grammar will be: stmt matchedstmt | unmatchedstmt if expr then matchedstmt else matchedstmt | otherstmts unmatchedstmt if expr then stmt | if expr then matchedstmt else unmatchedstmt 69
Ambiguity (cont. ) • We prefer the second parse tree (else matches with closest if). • So, we have to disambiguate our grammar to reflect this choice. • The unambiguous grammar will be: stmt matchedstmt | unmatchedstmt if expr then matchedstmt else matchedstmt | otherstmts unmatchedstmt if expr then stmt | if expr then matchedstmt else unmatchedstmt 69
 Ambiguity – Operator Precedence • Ambiguous grammars (because of ambiguous operators) can be disambiguated according to the precedence and associativity rules. E E+E | E*E | E^E | id | (E) disambiguate the grammar E E+T T T*F F G^F G id | precedence: ^ (right to left) * (left to right) + (left to right) | T | F | G (E) 70
Ambiguity – Operator Precedence • Ambiguous grammars (because of ambiguous operators) can be disambiguated according to the precedence and associativity rules. E E+E | E*E | E^E | id | (E) disambiguate the grammar E E+T T T*F F G^F G id | precedence: ^ (right to left) * (left to right) + (left to right) | T | F | G (E) 70
 Left Recursion • A grammar is left recursive if it has a non-terminal A such that there is a derivation. + A A for some string • Top-down parsing techniques cannot handle left-recursive grammars. • So, we have to convert our left-recursive grammar into an equivalent grammar which is not left-recursive. • The left-recursion may appear in a single step of the derivation (immediate left-recursion), or may appear in more than one step of the derivation. 71
Left Recursion • A grammar is left recursive if it has a non-terminal A such that there is a derivation. + A A for some string • Top-down parsing techniques cannot handle left-recursive grammars. • So, we have to convert our left-recursive grammar into an equivalent grammar which is not left-recursive. • The left-recursion may appear in a single step of the derivation (immediate left-recursion), or may appear in more than one step of the derivation. 71
 Immediate Left-Recursion A A | A A’ A’ A’ | where does not start with A eliminate immediate left recursion an equivalent grammar In general, A A 1 |. . . | A m | 1 |. . . | n where 1. . . n do not start with A eliminate immediate left recursion A 1 A’ |. . . | n A’ A’ 1 A’ |. . . | m A’ | an equivalent grammar 72
Immediate Left-Recursion A A | A A’ A’ A’ | where does not start with A eliminate immediate left recursion an equivalent grammar In general, A A 1 |. . . | A m | 1 |. . . | n where 1. . . n do not start with A eliminate immediate left recursion A 1 A’ |. . . | n A’ A’ 1 A’ |. . . | m A’ | an equivalent grammar 72
 Immediate Left-Recursion -- Example E E+T | T T T*F | F F id | (E) eliminate immediate left recursion E T E’ E’ +T E’ | T F T’ T’ *F T’ | F id | (E) 73
Immediate Left-Recursion -- Example E E+T | T T T*F | F F id | (E) eliminate immediate left recursion E T E’ E’ +T E’ | T F T’ T’ *F T’ | F id | (E) 73
 Left-Recursion -- Problem • A grammar cannot be immediately left-recursive, but it still can be left-recursive. • By just eliminating the immediate left-recursion, we may not get a grammar which is not left-recursive. S Aa | b A Sc | d This grammar is not immediately left-recursive, but it is still left-recursive. S Aa Sca A Sc Aac or causes to a left-recursion • So, we have to eliminate all left-recursions from our grammar 74
Left-Recursion -- Problem • A grammar cannot be immediately left-recursive, but it still can be left-recursive. • By just eliminating the immediate left-recursion, we may not get a grammar which is not left-recursive. S Aa | b A Sc | d This grammar is not immediately left-recursive, but it is still left-recursive. S Aa Sca A Sc Aac or causes to a left-recursion • So, we have to eliminate all left-recursions from our grammar 74
 Eliminate Left-Recursion -- Algorithm - Arrange non-terminals in some order: A 1. . . An - for i from 1 to n do { - for j from 1 to i-1 do { replace each production Ai Aj by Ai 1 |. . . | k where Aj 1 |. . . | k } - eliminate immediate left-recursions among Ai productions } 75
Eliminate Left-Recursion -- Algorithm - Arrange non-terminals in some order: A 1. . . An - for i from 1 to n do { - for j from 1 to i-1 do { replace each production Ai Aj by Ai 1 |. . . | k where Aj 1 |. . . | k } - eliminate immediate left-recursions among Ai productions } 75
 Eliminate Left-Recursion -- Example S Aa | b A Ac | Sd | f - Order of non-terminals: S, A for S: - we do not enter the inner loop. - there is no immediate left recursion in S. for A: - Replace A Sd with A Aad | bd So, we will have A Ac | Aad | bd | f - Eliminate the immediate left-recursion in A A bd. A’ | f. A’ A’ c. A’ | ad. A’ | So, the resulting equivalent grammar which is not left-recursive is: S Aa | b A bd. A’ | f. A’ A’ c. A’ | ad. A’ | 76
Eliminate Left-Recursion -- Example S Aa | b A Ac | Sd | f - Order of non-terminals: S, A for S: - we do not enter the inner loop. - there is no immediate left recursion in S. for A: - Replace A Sd with A Aad | bd So, we will have A Ac | Aad | bd | f - Eliminate the immediate left-recursion in A A bd. A’ | f. A’ A’ c. A’ | ad. A’ | So, the resulting equivalent grammar which is not left-recursive is: S Aa | b A bd. A’ | f. A’ A’ c. A’ | ad. A’ | 76
 Eliminate Left-Recursion – Example 2 S Aa | b A Ac | Sd | f - Order of non-terminals: A, S for A: - we do not enter the inner loop. - Eliminate the immediate left-recursion in A A Sd. A’ | f. A’ A’ c. A’ | for S: - Replace S Aa with S Sd. A’a | f. A’a So, we will have S Sd. A’a | f. A’a | b - Eliminate the immediate left-recursion in S S f. A’a. S’ | b. S’ S’ d. A’a. S’ | So, the resulting equivalent grammar which is not left-recursive is: S f. A’a. S’ | b. S’ S’ d. A’a. S’ | A Sd. A’ | f. A’ A’ c. A’ | 77
Eliminate Left-Recursion – Example 2 S Aa | b A Ac | Sd | f - Order of non-terminals: A, S for A: - we do not enter the inner loop. - Eliminate the immediate left-recursion in A A Sd. A’ | f. A’ A’ c. A’ | for S: - Replace S Aa with S Sd. A’a | f. A’a So, we will have S Sd. A’a | f. A’a | b - Eliminate the immediate left-recursion in S S f. A’a. S’ | b. S’ S’ d. A’a. S’ | So, the resulting equivalent grammar which is not left-recursive is: S f. A’a. S’ | b. S’ S’ d. A’a. S’ | A Sd. A’ | f. A’ A’ c. A’ | 77
 Left-Factoring • A predictive parser (a top-down parser without backtracking) insists that the grammar must be left-factored. grammar a new equivalent grammar suitable for predictive parsing stmt if expr then stmt else stmt if expr then stmt | • when we see if, we cannot now which production rule to choose to re -write stmt in the derivation. 78
Left-Factoring • A predictive parser (a top-down parser without backtracking) insists that the grammar must be left-factored. grammar a new equivalent grammar suitable for predictive parsing stmt if expr then stmt else stmt if expr then stmt | • when we see if, we cannot now which production rule to choose to re -write stmt in the derivation. 78
 Left-Factoring (cont. ) • In general, A 1 | 2 where is non-empty and the first symbols of 1 and 2 (if they have one)are different. • when processing we cannot know whether expand A to 1 or A to 2 • But, if we re-write the grammar as follows A A’ A’ 1 | 2 so, we can immediately expand A to A’ 79
Left-Factoring (cont. ) • In general, A 1 | 2 where is non-empty and the first symbols of 1 and 2 (if they have one)are different. • when processing we cannot know whether expand A to 1 or A to 2 • But, if we re-write the grammar as follows A A’ A’ 1 | 2 so, we can immediately expand A to A’ 79
 Left-Factoring -- Algorithm • For each non-terminal A with two or more alternatives (production rules) with a common non-empty prefix, let say A 1 |. . . | n | 1 |. . . | m convert it into A A’ | 1 |. . . | m A’ 1 |. . . | n 80
Left-Factoring -- Algorithm • For each non-terminal A with two or more alternatives (production rules) with a common non-empty prefix, let say A 1 |. . . | n | 1 |. . . | m convert it into A A’ | 1 |. . . | m A’ 1 |. . . | n 80
 Left-Factoring – Example 1 A ab. B | a. B | cdg | cde. B | cdf. B A a. A’ | cdg | cde. B | cdf. B A’ b. B | B A a. A’ | cd. A’’ A’ b. B | B A’’ g | e. B | f. B 81
Left-Factoring – Example 1 A ab. B | a. B | cdg | cde. B | cdf. B A a. A’ | cdg | cde. B | cdf. B A’ b. B | B A a. A’ | cd. A’’ A’ b. B | B A’’ g | e. B | f. B 81
 Left-Factoring – Example 2 A ad | abc | b A a. A’ | b A’ d | | bc A a. A’ | b A’ d | | b. A’’ | c 82
Left-Factoring – Example 2 A ad | abc | b A a. A’ | b A’ d | | bc A a. A’ | b A’ d | | b. A’’ | c 82
 Non-Context Free Language Constructs • There are some language constructions in the programming languages which are not context-free. This means that, we cannot write a contextfree grammar for these constructions. • L 1 = { c | is in (a|b)*} is not context-free declaring an identifier and checking whether it is declared or not later. We cannot do this with a context-free language. We need semantic analyzer (which is not context-free). • L 2 = {anbmcndm | n 1 and m 1 } is not context-free declaring two functions (one with n parameters, the other one with m parameters), and then calling them with actual parameters. 83
Non-Context Free Language Constructs • There are some language constructions in the programming languages which are not context-free. This means that, we cannot write a contextfree grammar for these constructions. • L 1 = { c | is in (a|b)*} is not context-free declaring an identifier and checking whether it is declared or not later. We cannot do this with a context-free language. We need semantic analyzer (which is not context-free). • L 2 = {anbmcndm | n 1 and m 1 } is not context-free declaring two functions (one with n parameters, the other one with m parameters), and then calling them with actual parameters. 83
 Top-Down Parsing • The parse tree is created top to bottom. • Top-down parser – Recursive-Descent Parsing • Backtracking is needed (If a choice of a production rule does not work, we backtrack to try other alternatives. ) • It is a general parsing technique, but not widely used. • Not efficient – Predictive Parsing • • • no backtracking efficient needs a special form of grammars (LL(1) grammars). Recursive Predictive Parsing is a special form of Recursive Descent parsing without backtracking. Non-Recursive (Table Driven) Predictive Parser is also known as LL(1) parser. 84
Top-Down Parsing • The parse tree is created top to bottom. • Top-down parser – Recursive-Descent Parsing • Backtracking is needed (If a choice of a production rule does not work, we backtrack to try other alternatives. ) • It is a general parsing technique, but not widely used. • Not efficient – Predictive Parsing • • • no backtracking efficient needs a special form of grammars (LL(1) grammars). Recursive Predictive Parsing is a special form of Recursive Descent parsing without backtracking. Non-Recursive (Table Driven) Predictive Parser is also known as LL(1) parser. 84
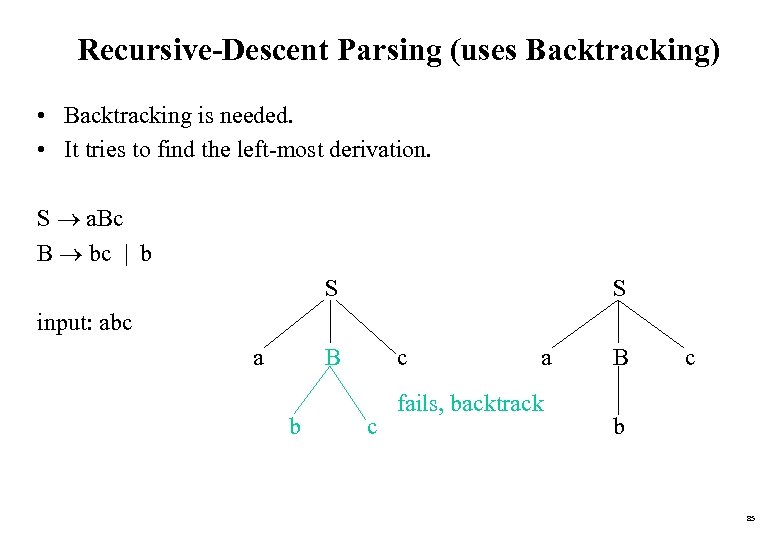 Recursive-Descent Parsing (uses Backtracking) • Backtracking is needed. • It tries to find the left-most derivation. S a. Bc B bc | b S S input: abc a B b c c a fails, backtrack B c b 85
Recursive-Descent Parsing (uses Backtracking) • Backtracking is needed. • It tries to find the left-most derivation. S a. Bc B bc | b S S input: abc a B b c c a fails, backtrack B c b 85
 Predictive Parser a grammar eliminate left recursion factor a grammar suitable for predictive parsing (a LL(1) grammar) no %100 guarantee. • When re-writing a non-terminal in a derivation step, a predictive parser can uniquely choose a production rule by just looking the current symbol in the input string. A 1 |. . . | n input: . . . a. . . . current token 86
Predictive Parser a grammar eliminate left recursion factor a grammar suitable for predictive parsing (a LL(1) grammar) no %100 guarantee. • When re-writing a non-terminal in a derivation step, a predictive parser can uniquely choose a production rule by just looking the current symbol in the input string. A 1 |. . . | n input: . . . a. . . . current token 86
 Predictive Parser (example) stmt if. . . while. . . begin. . . for. . . | | | • When we are trying to write the non-terminal stmt, if the current token is if we have to choose first production rule. • When we are trying to write the non-terminal stmt, we can uniquely choose the production rule by just looking the current token. • We eliminate the left recursion in the grammar, and left factor it. But it may not be suitable for predictive parsing (not LL(1) grammar). 87
Predictive Parser (example) stmt if. . . while. . . begin. . . for. . . | | | • When we are trying to write the non-terminal stmt, if the current token is if we have to choose first production rule. • When we are trying to write the non-terminal stmt, we can uniquely choose the production rule by just looking the current token. • We eliminate the left recursion in the grammar, and left factor it. But it may not be suitable for predictive parsing (not LL(1) grammar). 87
 Recursive Predictive Parsing • Each non-terminal corresponds to a procedure. Ex: A a. Bb (This is only the production rule for A) proc A { - match the current token with a, and move to the next token; - call ‘B’; - match the current token with b, and move to the next token; } 88
Recursive Predictive Parsing • Each non-terminal corresponds to a procedure. Ex: A a. Bb (This is only the production rule for A) proc A { - match the current token with a, and move to the next token; - call ‘B’; - match the current token with b, and move to the next token; } 88
 Recursive Predictive Parsing (cont. ) A a. Bb | b. AB proc A { case of the current token { ‘a’: - match the current token with a, and move to the next token; - call ‘B’; - match the current token with b, and move to the next token; ‘b’: - match the current token with b, and move to the next token; - call ‘A’; - call ‘B’; } } 89
Recursive Predictive Parsing (cont. ) A a. Bb | b. AB proc A { case of the current token { ‘a’: - match the current token with a, and move to the next token; - call ‘B’; - match the current token with b, and move to the next token; ‘b’: - match the current token with b, and move to the next token; - call ‘A’; - call ‘B’; } } 89
 Recursive Predictive Parsing (cont. ) • When to apply -productions. A a. A | b. B | • If all other productions fail, we should apply an -production. For example, if the current token is not a or b, we may apply the -production. • Most correct choice: We should apply an -production for a nonterminal A when the current token is in the follow set of A (which terminals can follow A in the sentential forms). 90
Recursive Predictive Parsing (cont. ) • When to apply -productions. A a. A | b. B | • If all other productions fail, we should apply an -production. For example, if the current token is not a or b, we may apply the -production. • Most correct choice: We should apply an -production for a nonterminal A when the current token is in the follow set of A (which terminals can follow A in the sentential forms). 90
 Recursive Predictive Parsing (Example) A a. Be | c. Bd | C B b. B | C f proc C { proc A { case of the current token { a: - match the current token with a, and move to the next token; - call B; - match the current token with e, and move to the next token; c: - match the current token with c, and move to the next token; - call B; - match the current token with d, and move to the next token; f: - call C } first set of C } match the current token with f, and move to the next token; } proc B { case of the current token { b: - match the current token with b, and move to the next token; - call B e, d: do nothing } } BİL 744 Derleyici Gerçekleştirimi (Compiler Design) follow set of B 91
Recursive Predictive Parsing (Example) A a. Be | c. Bd | C B b. B | C f proc C { proc A { case of the current token { a: - match the current token with a, and move to the next token; - call B; - match the current token with e, and move to the next token; c: - match the current token with c, and move to the next token; - call B; - match the current token with d, and move to the next token; f: - call C } first set of C } match the current token with f, and move to the next token; } proc B { case of the current token { b: - match the current token with b, and move to the next token; - call B e, d: do nothing } } BİL 744 Derleyici Gerçekleştirimi (Compiler Design) follow set of B 91
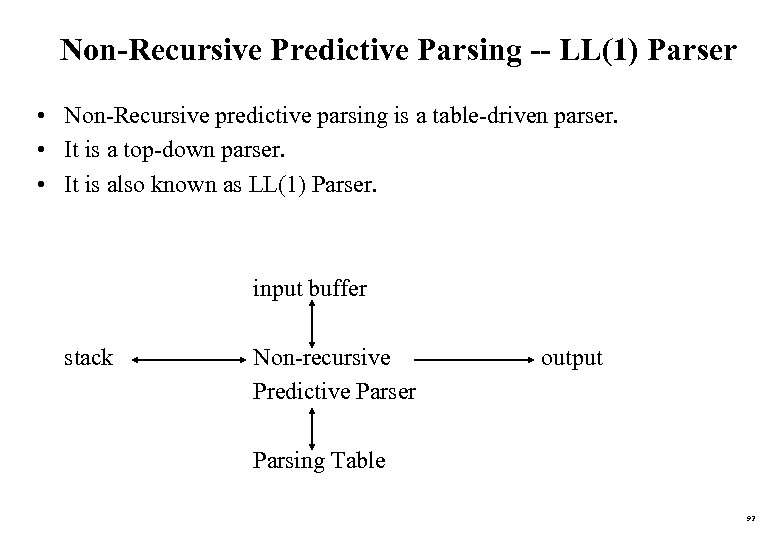 Non-Recursive Predictive Parsing -- LL(1) Parser • Non-Recursive predictive parsing is a table-driven parser. • It is a top-down parser. • It is also known as LL(1) Parser. input buffer stack Non-recursive Predictive Parser output Parsing Table 92
Non-Recursive Predictive Parsing -- LL(1) Parser • Non-Recursive predictive parsing is a table-driven parser. • It is a top-down parser. • It is also known as LL(1) Parser. input buffer stack Non-recursive Predictive Parser output Parsing Table 92
 LL(1) Parser input buffer – our string to be parsed. We will assume that its end is marked with a special symbol $. output – a production rule representing a step of the derivation sequence (left-most derivation) of the string in the input buffer. stack – – contains the grammar symbols at the bottom of the stack, there is a special end marker symbol $. initially the stack contains only the symbol $ and the starting symbol S. $S initial stack when the stack is emptied (ie. only $ left in the stack), the parsing is completed. parsing table – – a two-dimensional array M[A, a] each row is a non-terminal symbol each column is a terminal symbol or the special symbol $ each entry holds a production rule. 93
LL(1) Parser input buffer – our string to be parsed. We will assume that its end is marked with a special symbol $. output – a production rule representing a step of the derivation sequence (left-most derivation) of the string in the input buffer. stack – – contains the grammar symbols at the bottom of the stack, there is a special end marker symbol $. initially the stack contains only the symbol $ and the starting symbol S. $S initial stack when the stack is emptied (ie. only $ left in the stack), the parsing is completed. parsing table – – a two-dimensional array M[A, a] each row is a non-terminal symbol each column is a terminal symbol or the special symbol $ each entry holds a production rule. 93
 LL(1) Parser – Parser Actions • • The symbol at the top of the stack (say X) and the current symbol in the input string (say a) determine the parser action. There are four possible parser actions. 1. If X and a are $ parser halts (successful completion) 2. If X and a are the same terminal symbol (different from $) parser pops X from the stack, and moves the next symbol in the input buffer. 3. If X is a non-terminal Parser looks at the parsing table entry M[X, a]. If M[X, a] holds a production rule X Y 1 Y 2. . . Yk, it pops X from the stack, and pushes Yk, Yk-1, . . . , Y 1 into the stack. The parser also outputs the production rule X Y 1 Y 2. . . Yk to represent a step of the derivation. 4. none of the above error – – all empty entries in the parsing table are errors. If X is a terminal symbol different from a, this is also an error case. 94
LL(1) Parser – Parser Actions • • The symbol at the top of the stack (say X) and the current symbol in the input string (say a) determine the parser action. There are four possible parser actions. 1. If X and a are $ parser halts (successful completion) 2. If X and a are the same terminal symbol (different from $) parser pops X from the stack, and moves the next symbol in the input buffer. 3. If X is a non-terminal Parser looks at the parsing table entry M[X, a]. If M[X, a] holds a production rule X Y 1 Y 2. . . Yk, it pops X from the stack, and pushes Yk, Yk-1, . . . , Y 1 into the stack. The parser also outputs the production rule X Y 1 Y 2. . . Yk to represent a step of the derivation. 4. none of the above error – – all empty entries in the parsing table are errors. If X is a terminal symbol different from a, this is also an error case. 94
 LL(1) Parser – Example-1 S a. Ba B b. B | a b S S a. Ba B B $ LL(1) Parsing Table B b. B stack input output $S $a. Ba $a. Bb $a. B $a $ abba$ ba$ a$ a$ $ S a. Ba B b. B B accept, successful completion 95
LL(1) Parser – Example-1 S a. Ba B b. B | a b S S a. Ba B B $ LL(1) Parsing Table B b. B stack input output $S $a. Ba $a. Bb $a. B $a $ abba$ ba$ a$ a$ $ S a. Ba B b. B B accept, successful completion 95
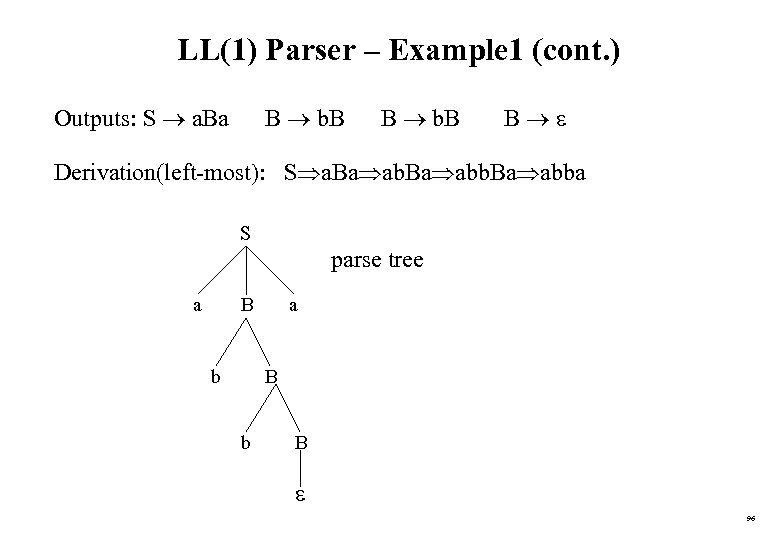 LL(1) Parser – Example 1 (cont. ) Outputs: S a. Ba B b. B B Derivation(left-most): S a. Ba abba S parse tree a B b B 96
LL(1) Parser – Example 1 (cont. ) Outputs: S a. Ba B b. B B Derivation(left-most): S a. Ba abba S parse tree a B b B 96
 LL(1) Parser – Example-2 E TE’ E’ +TE’ | T FT’ T’ *FT’ | F (E) | id E E’ T T’ F id E TE’ + * ( E TE’ E’ +TE’ $ E’ T FT’ E’ T’ T’ T FT’ T’ F id ) T’ *FT’ F (E) 97
LL(1) Parser – Example-2 E TE’ E’ +TE’ | T FT’ T’ *FT’ | F (E) | id E E’ T T’ F id E TE’ + * ( E TE’ E’ +TE’ $ E’ T FT’ E’ T’ T’ T FT’ T’ F id ) T’ *FT’ F (E) 97
 LL(1) Parser – Example 2 stack $E $E’T $E’ T’F $ E’ T’id $ E’ T’ $ E’ T+ $ E’ T’ F $ E’ T’id $ E’ T’ $ E’ $ input id+id$ +id$ id$ $ $ $ output E TE’ T FT’ F id T’ E’ +TE’ T FT’ F id T’ E’ accept 98
LL(1) Parser – Example 2 stack $E $E’T $E’ T’F $ E’ T’id $ E’ T’ $ E’ T+ $ E’ T’ F $ E’ T’id $ E’ T’ $ E’ $ input id+id$ +id$ id$ $ $ $ output E TE’ T FT’ F id T’ E’ +TE’ T FT’ F id T’ E’ accept 98
 Constructing LL(1) Parsing Tables • Two functions are used in the construction of LL(1) parsing tables: – FIRST FOLLOW • FIRST( ) is a set of the terminal symbols which occur as first symbols in strings derived from where is any string of grammar symbols. • if derives to , then is also in FIRST( ). • FOLLOW(A) is the set of the terminals which occur immediately after (follow) the non-terminal A in the strings derived from the starting symbol. * – a terminal a is in FOLLOW(A) if S Aa * – $ is in FOLLOW(A) if S A 99
Constructing LL(1) Parsing Tables • Two functions are used in the construction of LL(1) parsing tables: – FIRST FOLLOW • FIRST( ) is a set of the terminal symbols which occur as first symbols in strings derived from where is any string of grammar symbols. • if derives to , then is also in FIRST( ). • FOLLOW(A) is the set of the terminals which occur immediately after (follow) the non-terminal A in the strings derived from the starting symbol. * – a terminal a is in FOLLOW(A) if S Aa * – $ is in FOLLOW(A) if S A 99
 Compute FIRST for Any String X • If X is a terminal symbol FIRST(X)={X} • If X is a non-terminal symbol and X is a production rule is in FIRST(X). • If X is a non-terminal symbol and X Y 1 Y 2. . Yn is a production rule if a terminal a in FIRST(Yi) and is in all FIRST(Yj) for j=1, . . . , i-1 then a is in FIRST(X). if is in all FIRST(Yj) for j=1, . . . , n then is in FIRST(X). • If X is FIRST(X)={ } • If X is Y 1 Y 2. . Yn if a terminal a in FIRST(Yi) and is in all FIRST(Yj) for j=1, . . . , i-1 then a is in FIRST(X). if is in all FIRST(Yj) for j=1, . . . , n then is in FIRST(X). 100
Compute FIRST for Any String X • If X is a terminal symbol FIRST(X)={X} • If X is a non-terminal symbol and X is a production rule is in FIRST(X). • If X is a non-terminal symbol and X Y 1 Y 2. . Yn is a production rule if a terminal a in FIRST(Yi) and is in all FIRST(Yj) for j=1, . . . , i-1 then a is in FIRST(X). if is in all FIRST(Yj) for j=1, . . . , n then is in FIRST(X). • If X is FIRST(X)={ } • If X is Y 1 Y 2. . Yn if a terminal a in FIRST(Yi) and is in all FIRST(Yj) for j=1, . . . , i-1 then a is in FIRST(X). if is in all FIRST(Yj) for j=1, . . . , n then is in FIRST(X). 100
 FIRST Example E TE’ E’ +TE’ | T FT’ T’ *FT’ | F (E) | id FIRST(F) = {(, id} FIRST(T’) = {*, } FIRST(T) = {(, id} FIRST(E’) = {+, } FIRST(E) = {(, id} FIRST(TE’) = {(, id} FIRST(+TE’ ) = {+} FIRST( ) = { } FIRST(FT’) = {(, id} FIRST(*FT’) = {*} FIRST( ) = { } FIRST((E)) = {(} FIRST(id) = {id} 101
FIRST Example E TE’ E’ +TE’ | T FT’ T’ *FT’ | F (E) | id FIRST(F) = {(, id} FIRST(T’) = {*, } FIRST(T) = {(, id} FIRST(E’) = {+, } FIRST(E) = {(, id} FIRST(TE’) = {(, id} FIRST(+TE’ ) = {+} FIRST( ) = { } FIRST(FT’) = {(, id} FIRST(*FT’) = {*} FIRST( ) = { } FIRST((E)) = {(} FIRST(id) = {id} 101
 Compute FOLLOW (for non-terminals) • If S is the start symbol $ is in FOLLOW(S) • if A B is a production rule everything in FIRST( ) is FOLLOW(B) except • If ( A B is a production rule ) or ( A B is a production rule and is in FIRST( ) ) everything in FOLLOW(A) is in FOLLOW(B). We apply these rules until nothing more can be added to any follow set. 102
Compute FOLLOW (for non-terminals) • If S is the start symbol $ is in FOLLOW(S) • if A B is a production rule everything in FIRST( ) is FOLLOW(B) except • If ( A B is a production rule ) or ( A B is a production rule and is in FIRST( ) ) everything in FOLLOW(A) is in FOLLOW(B). We apply these rules until nothing more can be added to any follow set. 102
 FOLLOW Example E TE’ E’ +TE’ | T FT’ T’ *FT’ | F (E) | id FOLLOW(E) = { $, ) } FOLLOW(E’) = { $, ) } FOLLOW(T) = { +, ), $ } FOLLOW(T’) = { +, ), $ } FOLLOW(F) = {+, *, ), $ } 103
FOLLOW Example E TE’ E’ +TE’ | T FT’ T’ *FT’ | F (E) | id FOLLOW(E) = { $, ) } FOLLOW(E’) = { $, ) } FOLLOW(T) = { +, ), $ } FOLLOW(T’) = { +, ), $ } FOLLOW(F) = {+, *, ), $ } 103
 Constructing LL(1) Parsing Table -- Algorithm • for each production rule A of a grammar G – for each terminal a in FIRST( ) add A to M[A, a] – If in FIRST( ) for each terminal a in FOLLOW(A) add A to M[A, a] – If in FIRST( ) and $ in FOLLOW(A) add A to M[A, $] • All other undefined entries of the parsing table are error entries. 104
Constructing LL(1) Parsing Table -- Algorithm • for each production rule A of a grammar G – for each terminal a in FIRST( ) add A to M[A, a] – If in FIRST( ) for each terminal a in FOLLOW(A) add A to M[A, a] – If in FIRST( ) and $ in FOLLOW(A) add A to M[A, $] • All other undefined entries of the parsing table are error entries. 104
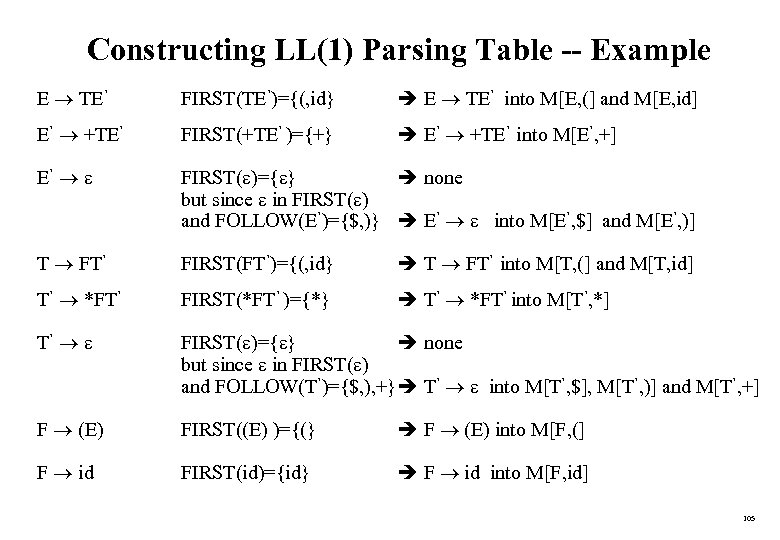 Constructing LL(1) Parsing Table -- Example E TE’ FIRST(TE’)={(, id} E TE’ into M[E, (] and M[E, id] E’ +TE’ FIRST(+TE’ )={+} E’ +TE’ into M[E’, +] E’ FIRST( )={ } none but since in FIRST( ) and FOLLOW(E’)={$, )} E’ into M[E’, $] and M[E’, )] T FT’ FIRST(FT’)={(, id} T FT’ into M[T, (] and M[T, id] T’ *FT’ FIRST(*FT’ )={*} T’ *FT’ into M[T’, *] T’ FIRST( )={ } none but since in FIRST( ) and FOLLOW(T’)={$, ), +} T’ into M[T’, $], M[T’, )] and M[T’, +] F (E) FIRST((E) )={(} F (E) into M[F, (] F id FIRST(id)={id} F id into M[F, id] 105
Constructing LL(1) Parsing Table -- Example E TE’ FIRST(TE’)={(, id} E TE’ into M[E, (] and M[E, id] E’ +TE’ FIRST(+TE’ )={+} E’ +TE’ into M[E’, +] E’ FIRST( )={ } none but since in FIRST( ) and FOLLOW(E’)={$, )} E’ into M[E’, $] and M[E’, )] T FT’ FIRST(FT’)={(, id} T FT’ into M[T, (] and M[T, id] T’ *FT’ FIRST(*FT’ )={*} T’ *FT’ into M[T’, *] T’ FIRST( )={ } none but since in FIRST( ) and FOLLOW(T’)={$, ), +} T’ into M[T’, $], M[T’, )] and M[T’, +] F (E) FIRST((E) )={(} F (E) into M[F, (] F id FIRST(id)={id} F id into M[F, id] 105
 LL(1) Grammars • A grammar whose parsing table has no multiply-defined entries is said to be LL(1) grammar. one input symbol used as a look-head symbol do determine parser action LL(1) left most derivation input scanned from left to right • The parsing table of a grammar may contain more than one production rule. In this case, we say that it is not a LL(1) grammar. 106
LL(1) Grammars • A grammar whose parsing table has no multiply-defined entries is said to be LL(1) grammar. one input symbol used as a look-head symbol do determine parser action LL(1) left most derivation input scanned from left to right • The parsing table of a grammar may contain more than one production rule. In this case, we say that it is not a LL(1) grammar. 106
 A Grammar which is not LL(1) S i. Ct. SE | E e. S | C b a FIRST(i. Ct. SE) = {i} FIRST(a) = {a} FIRST(e. S) = {e} FIRST( ) = { } FIRST(b) = {b} FOLLOW(S) = { $, e } FOLLOW(E) = { $, e } FOLLOW(C) = { t } a b e S S a t $ S i. Ct. SE E e. S E E C i E C b two production rules for M[E, e] Problem ambiguity 107
A Grammar which is not LL(1) S i. Ct. SE | E e. S | C b a FIRST(i. Ct. SE) = {i} FIRST(a) = {a} FIRST(e. S) = {e} FIRST( ) = { } FIRST(b) = {b} FOLLOW(S) = { $, e } FOLLOW(E) = { $, e } FOLLOW(C) = { t } a b e S S a t $ S i. Ct. SE E e. S E E C i E C b two production rules for M[E, e] Problem ambiguity 107
 A Grammar which is not LL(1) (cont. ) • What do we have to do it if the resulting parsing table contains multiply defined entries? – If we didn’t eliminate left recursion, eliminate the left recursion in the grammar. – If the grammar is not left factored, we have to left factor the grammar. – If its (new grammar’s) parsing table still contains multiply defined entries, that grammar is ambiguous or it is inherently not a LL(1) grammar. • A left recursive grammar cannot be a LL(1) grammar. – A A | any terminal that appears in FIRST( ) also appears FIRST(A ) because A . If is , any terminal that appears in FIRST( ) also appears in FIRST(A ) and FOLLOW(A). • A grammar is not left factored, it cannot be a LL(1) grammar • A 1 | 2 any terminal that appears in FIRST( 1) also appears in FIRST( 2). • An ambiguous grammar cannot be a LL(1) grammar. 108
A Grammar which is not LL(1) (cont. ) • What do we have to do it if the resulting parsing table contains multiply defined entries? – If we didn’t eliminate left recursion, eliminate the left recursion in the grammar. – If the grammar is not left factored, we have to left factor the grammar. – If its (new grammar’s) parsing table still contains multiply defined entries, that grammar is ambiguous or it is inherently not a LL(1) grammar. • A left recursive grammar cannot be a LL(1) grammar. – A A | any terminal that appears in FIRST( ) also appears FIRST(A ) because A . If is , any terminal that appears in FIRST( ) also appears in FIRST(A ) and FOLLOW(A). • A grammar is not left factored, it cannot be a LL(1) grammar • A 1 | 2 any terminal that appears in FIRST( 1) also appears in FIRST( 2). • An ambiguous grammar cannot be a LL(1) grammar. 108
 Properties of LL(1) Grammars • A grammar G is LL(1) if and only if the following conditions hold for two distinctive production rules A and A 1. Both and cannot derive strings starting with same terminals. 2. At most one of and can derive to . 3. If can derive to , then cannot derive to any string starting with a terminal in FOLLOW(A). 109
Properties of LL(1) Grammars • A grammar G is LL(1) if and only if the following conditions hold for two distinctive production rules A and A 1. Both and cannot derive strings starting with same terminals. 2. At most one of and can derive to . 3. If can derive to , then cannot derive to any string starting with a terminal in FOLLOW(A). 109
 Error Recovery in Predictive Parsing • An error may occur in the predictive parsing (LL(1) parsing) – if the terminal symbol on the top of stack does not match with the current input symbol. – if the top of stack is a non-terminal A, the current input symbol is a, and the parsing table entry M[A, a] is empty. • What should the parser do in an error case? – The parser should be able to give an error message (as much as possible meaningful error message). – It should be recover from that error case, and it should be able to continue the parsing with the rest of the input. 110
Error Recovery in Predictive Parsing • An error may occur in the predictive parsing (LL(1) parsing) – if the terminal symbol on the top of stack does not match with the current input symbol. – if the top of stack is a non-terminal A, the current input symbol is a, and the parsing table entry M[A, a] is empty. • What should the parser do in an error case? – The parser should be able to give an error message (as much as possible meaningful error message). – It should be recover from that error case, and it should be able to continue the parsing with the rest of the input. 110
 Error Recovery Techniques • Panic-Mode Error Recovery – Skipping the input symbols until a synchronizing token is found. • Phrase-Level Error Recovery – Each empty entry in the parsing table is filled with a pointer to a specific error routine to take care that error case. • Error-Productions – If we have a good idea of the common errors that might be encountered, we can augment the grammar with productions that generate erroneous constructs. – When an error production is used by the parser, we can generate appropriate error diagnostics. – Since it is almost impossible to know all the errors that can be made by the programmers, this method is not practical. • Global-Correction – Ideally, we would like a compiler to make as few change as possible in processing incorrect inputs. – We have to globally analyze the input to find the error. – This is an expensive method, and it is not in practice. 111
Error Recovery Techniques • Panic-Mode Error Recovery – Skipping the input symbols until a synchronizing token is found. • Phrase-Level Error Recovery – Each empty entry in the parsing table is filled with a pointer to a specific error routine to take care that error case. • Error-Productions – If we have a good idea of the common errors that might be encountered, we can augment the grammar with productions that generate erroneous constructs. – When an error production is used by the parser, we can generate appropriate error diagnostics. – Since it is almost impossible to know all the errors that can be made by the programmers, this method is not practical. • Global-Correction – Ideally, we would like a compiler to make as few change as possible in processing incorrect inputs. – We have to globally analyze the input to find the error. – This is an expensive method, and it is not in practice. 111
 Panic-Mode Error Recovery in LL(1) Parsing • In panic-mode error recovery, we skip all the input symbols until a synchronizing token is found. • What is the synchronizing token? – All the terminal-symbols in the follow set of a non-terminal can be used as a synchronizing token set for that non-terminal. • So, a simple panic-mode error recovery for the LL(1) parsing: – All the empty entries are marked as synch to indicate that the parser will skip all the input symbols until a symbol in the follow set of the non-terminal A which on the top of the stack. Then the parser will pop that non-terminal A from the stack. The parsing continues from that state. – To handle unmatched terminal symbols, the parser pops that unmatched terminal symbol from the stack and it issues an error message saying that unmatched terminal is inserted. 112
Panic-Mode Error Recovery in LL(1) Parsing • In panic-mode error recovery, we skip all the input symbols until a synchronizing token is found. • What is the synchronizing token? – All the terminal-symbols in the follow set of a non-terminal can be used as a synchronizing token set for that non-terminal. • So, a simple panic-mode error recovery for the LL(1) parsing: – All the empty entries are marked as synch to indicate that the parser will skip all the input symbols until a symbol in the follow set of the non-terminal A which on the top of the stack. Then the parser will pop that non-terminal A from the stack. The parsing continues from that state. – To handle unmatched terminal symbols, the parser pops that unmatched terminal symbol from the stack and it issues an error message saying that unmatched terminal is inserted. 112
 Panic-Mode Error Recovery - Example a S Ab. S | e | A a | c. Ad input aab$ ab$ ab$ b$ $ $ c d e $ S S Ab. S sync S Ab. S FOLLOW(S)={$} FOLLOW(A)={b, d} stack $S $Sb. A $Sba $Sb $S $ b sync S e S A A a sync output S Ab. S A a Error: missing b, inserted S Ab. S A a S accept sync A c. Ad sync stack input output $S ceadb$ S Ab. S $Sb. A ceadb$ A c. Ad $Sbd. Ac ceadb$ $Sbd. A eadb$ Error: unexpected e (illegal A) (Remove all input tokens until first b or d, pop A) $Sbd db$ $Sb b$ $S $ S $ $ accept 113
Panic-Mode Error Recovery - Example a S Ab. S | e | A a | c. Ad input aab$ ab$ ab$ b$ $ $ c d e $ S S Ab. S sync S Ab. S FOLLOW(S)={$} FOLLOW(A)={b, d} stack $S $Sb. A $Sba $Sb $S $ b sync S e S A A a sync output S Ab. S A a Error: missing b, inserted S Ab. S A a S accept sync A c. Ad sync stack input output $S ceadb$ S Ab. S $Sb. A ceadb$ A c. Ad $Sbd. Ac ceadb$ $Sbd. A eadb$ Error: unexpected e (illegal A) (Remove all input tokens until first b or d, pop A) $Sbd db$ $Sb b$ $S $ S $ $ accept 113
 Phrase-Level Error Recovery • Each empty entry in the parsing table is filled with a pointer to a special error routine which will take care that error case. • These error routines may: – change, insert, or delete input symbols. – issue appropriate error messages – pop items from the stack. • We should be careful when we design these error routines, because we may put the parser into an infinite loop. 114
Phrase-Level Error Recovery • Each empty entry in the parsing table is filled with a pointer to a special error routine which will take care that error case. • These error routines may: – change, insert, or delete input symbols. – issue appropriate error messages – pop items from the stack. • We should be careful when we design these error routines, because we may put the parser into an infinite loop. 114
 Bottom-Up Parsing • A bottom-up parser creates the parse tree of the given input starting from leaves towards the root. • A bottom-up parser tries to find the right-most derivation of the given input in the reverse order. S . . . (the right-most derivation of ) (the bottom-up parser finds the right-most derivation in the reverse order) • Bottom-up parsing is also known as shift-reduce parsing because its two main actions are shift and reduce. – At each shift action, the current symbol in the input string is pushed to a stack. – At each reduction step, the symbols at the top of the stack (this symbol sequence is the right side of a production) will replaced by the non-terminal at the left side of that production. – There also two more actions: accept and error. 115
Bottom-Up Parsing • A bottom-up parser creates the parse tree of the given input starting from leaves towards the root. • A bottom-up parser tries to find the right-most derivation of the given input in the reverse order. S . . . (the right-most derivation of ) (the bottom-up parser finds the right-most derivation in the reverse order) • Bottom-up parsing is also known as shift-reduce parsing because its two main actions are shift and reduce. – At each shift action, the current symbol in the input string is pushed to a stack. – At each reduction step, the symbols at the top of the stack (this symbol sequence is the right side of a production) will replaced by the non-terminal at the left side of that production. – There also two more actions: accept and error. 115
 Shift-Reduce Parsing • A shift-reduce parser tries to reduce the given input string into the starting symbol. a string the starting symbol reduced to • At each reduction step, a substring of the input matching to the right side of a production rule is replaced by the non-terminal at the left side of that production rule. • If the substring is chosen correctly, the right most derivation of that string is created in the reverse order. Rightmost Derivation: Shift-Reduce Parser finds: * S rm rm . . . S rm 116
Shift-Reduce Parsing • A shift-reduce parser tries to reduce the given input string into the starting symbol. a string the starting symbol reduced to • At each reduction step, a substring of the input matching to the right side of a production rule is replaced by the non-terminal at the left side of that production rule. • If the substring is chosen correctly, the right most derivation of that string is created in the reverse order. Rightmost Derivation: Shift-Reduce Parser finds: * S rm rm . . . S rm 116
 Shift-Reduce Parsing -- Example S a. ABb A a. A | a B b. B | b input string: aaabb aa. Abb a. ABb S reduction S rm a. ABb a. Abb rm aa. Abb aaabb rm rm Right Sentential Forms • How do we know which substring to be replaced at each reduction step? 117
Shift-Reduce Parsing -- Example S a. ABb A a. A | a B b. B | b input string: aaabb aa. Abb a. ABb S reduction S rm a. ABb a. Abb rm aa. Abb aaabb rm rm Right Sentential Forms • How do we know which substring to be replaced at each reduction step? 117
 Handle • Informally, a handle of a string is a substring that matches the right side of a production rule. – But not every substring matches the right side of a production rule is handle • A handle of a right sentential form ( ) is a production rule A and a position of where the string may be found and replaced by A to produce the previous right-sentential form in a rightmost derivation of . * S rm A rm • If the grammar is unambiguous, then every right-sentential form of the grammar has exactly one handle. • We will see that is a string of terminals. 118
Handle • Informally, a handle of a string is a substring that matches the right side of a production rule. – But not every substring matches the right side of a production rule is handle • A handle of a right sentential form ( ) is a production rule A and a position of where the string may be found and replaced by A to produce the previous right-sentential form in a rightmost derivation of . * S rm A rm • If the grammar is unambiguous, then every right-sentential form of the grammar has exactly one handle. • We will see that is a string of terminals. 118
 Handle Pruning • A right-most derivation in reverse can be obtained by handle-pruning. S= 0 1 rm 2 rm. . . rm n-1 n= rm rm input string • Start from n, find a handle An n in n, and replace n in by An to get n-1. • Then find a handle An-1 in n-1, replace n-1 in by An-1 to get n-2. • Repeat this, until we reach S. and 119
Handle Pruning • A right-most derivation in reverse can be obtained by handle-pruning. S= 0 1 rm 2 rm. . . rm n-1 n= rm rm input string • Start from n, find a handle An n in n, and replace n in by An to get n-1. • Then find a handle An-1 in n-1, replace n-1 in by An-1 to get n-2. • Repeat this, until we reach S. and 119
 A Shift-Reduce Parser E E+T | T T T*F | F F (E) | id Right-Most Derivation of id+id*id E E+T*F E+T*id E+F*id E+id*id T+id*id F+id*id id+id*id Right-Most Sentential Form Reducing Production id+id*id F id F+id*id T F T+id*id E T E+id*id F id E+F*id T F E+T*id F id E+T*F T T*F E+T E Handles are red and underlined in the right-sentential forms. 120
A Shift-Reduce Parser E E+T | T T T*F | F F (E) | id Right-Most Derivation of id+id*id E E+T*F E+T*id E+F*id E+id*id T+id*id F+id*id id+id*id Right-Most Sentential Form Reducing Production id+id*id F id F+id*id T F T+id*id E T E+id*id F id E+F*id T F E+T*id F id E+T*F T T*F E+T E Handles are red and underlined in the right-sentential forms. 120
 A Stack Implementation of A Shift-Reduce Parser • There are four possible actions of a shift-parser action: 1. Shift : The next input symbol is shifted onto the top of the stack. 2. Reduce: Replace the handle on the top of the stack by the nonterminal. 3. Accept: Successful completion of parsing. 4. Error: Parser discovers a syntax error, and calls an error recovery routine. • • Initial stack just contains only the end-marker $. The end of the input string is marked by the end-marker $. 121
A Stack Implementation of A Shift-Reduce Parser • There are four possible actions of a shift-parser action: 1. Shift : The next input symbol is shifted onto the top of the stack. 2. Reduce: Replace the handle on the top of the stack by the nonterminal. 3. Accept: Successful completion of parsing. 4. Error: Parser discovers a syntax error, and calls an error recovery routine. • • Initial stack just contains only the end-marker $. The end of the input string is marked by the end-marker $. 121
 A Stack Implementation of A Shift-Reduce Parser Stack Input Action $ $id $F $T $E $E+id $E+F $E+T*id $E+T*F $E+T $E id+id*id$ shift +id*id$ id*id$ id$ $ $ reduce by F id reduce by T F reduce by E T shift reduce by F id reduce by T F shift reduce by F id reduce by T T*F reduce by E E+T accept Parse Tree E 8 E 3 + T 7 T 2 T 5 * F 1 F 4 id id F 6 id 122
A Stack Implementation of A Shift-Reduce Parser Stack Input Action $ $id $F $T $E $E+id $E+F $E+T*id $E+T*F $E+T $E id+id*id$ shift +id*id$ id*id$ id$ $ $ reduce by F id reduce by T F reduce by E T shift reduce by F id reduce by T F shift reduce by F id reduce by T T*F reduce by E E+T accept Parse Tree E 8 E 3 + T 7 T 2 T 5 * F 1 F 4 id id F 6 id 122
 Conflicts During Shift-Reduce Parsing • There are context-free grammars for which shift-reduce parsers cannot be used. • Stack contents and the next input symbol may not decide action: – shift/reduce conflict: Whether make a shift operation or a reduction. – reduce/reduce conflict: The parser cannot decide which of several reductions to make. • If a shift-reduce parser cannot be used for a grammar, that grammar is called as non-LR(k) grammar. left to right scanning right-most derivation k lookhead • An ambiguous grammar can never be a LR grammar. 123
Conflicts During Shift-Reduce Parsing • There are context-free grammars for which shift-reduce parsers cannot be used. • Stack contents and the next input symbol may not decide action: – shift/reduce conflict: Whether make a shift operation or a reduction. – reduce/reduce conflict: The parser cannot decide which of several reductions to make. • If a shift-reduce parser cannot be used for a grammar, that grammar is called as non-LR(k) grammar. left to right scanning right-most derivation k lookhead • An ambiguous grammar can never be a LR grammar. 123
 Shift-Reduce Parsers • There are two main categories of shift-reduce parsers 1. Operator-Precedence Parser – simple, but only a small class of grammars. CFG LR LALR 2. LR-Parsers SLR – covers wide range of grammars. • SLR – simple LR parser • LR – most general LR parser • LALR – intermediate LR parser (lookhead LR parser) – SLR, LR and LALR work same, only their parsing tables are different. 124
Shift-Reduce Parsers • There are two main categories of shift-reduce parsers 1. Operator-Precedence Parser – simple, but only a small class of grammars. CFG LR LALR 2. LR-Parsers SLR – covers wide range of grammars. • SLR – simple LR parser • LR – most general LR parser • LALR – intermediate LR parser (lookhead LR parser) – SLR, LR and LALR work same, only their parsing tables are different. 124
 LR Parsers • The most powerful shift-reduce parsing (yet efficient) is: LR(k) parsing. left to right scanning right-most derivation k lookhead (k is omitted it is 1) • LR parsing is attractive because: – LR parsing is most general non-backtracking shift-reduce parsing, yet it is still efficient. – The class of grammars that can be parsed using LR methods is a proper superset of the class of grammars that can be parsed with predictive parsers. LL(1)-Grammars LR(1)-Grammars – An LR-parser can detect a syntactic error as soon as it is possible to do so a left-to-right scan of the input. 125
LR Parsers • The most powerful shift-reduce parsing (yet efficient) is: LR(k) parsing. left to right scanning right-most derivation k lookhead (k is omitted it is 1) • LR parsing is attractive because: – LR parsing is most general non-backtracking shift-reduce parsing, yet it is still efficient. – The class of grammars that can be parsed using LR methods is a proper superset of the class of grammars that can be parsed with predictive parsers. LL(1)-Grammars LR(1)-Grammars – An LR-parser can detect a syntactic error as soon as it is possible to do so a left-to-right scan of the input. 125
 LR Parsers • LR-Parsers – covers wide range of grammars. – SLR – simple LR parser – LR – most general LR parser – LALR – intermediate LR parser (look-head LR parser) – SLR, LR and LALR work same (they used the same algorithm), only their parsing tables are different. 126
LR Parsers • LR-Parsers – covers wide range of grammars. – SLR – simple LR parser – LR – most general LR parser – LALR – intermediate LR parser (look-head LR parser) – SLR, LR and LALR work same (they used the same algorithm), only their parsing tables are different. 126
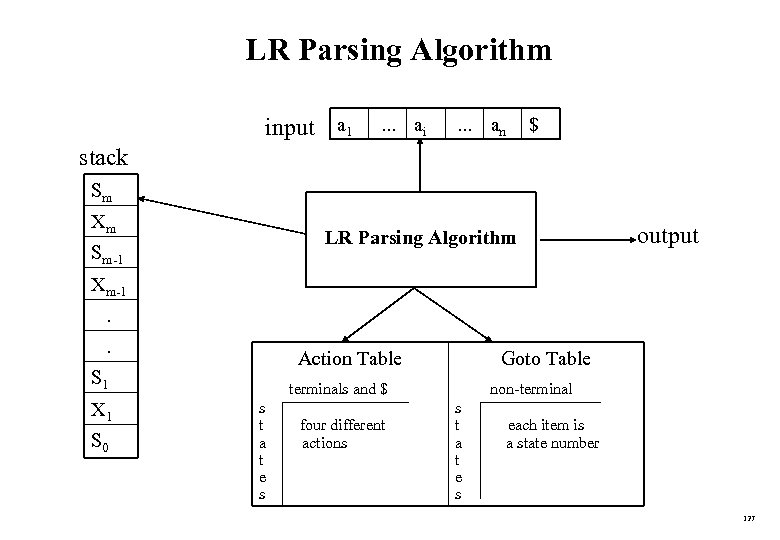 LR Parsing Algorithm input a 1 . . . ai . . . an $ stack Sm Xm LR Parsing Algorithm Sm-1 output Xm-1. . Action Table S 1 X 1 S 0 Goto Table terminals and $ s t a t e s four different actions non-terminal s t a t e s each item is a state number 127
LR Parsing Algorithm input a 1 . . . ai . . . an $ stack Sm Xm LR Parsing Algorithm Sm-1 output Xm-1. . Action Table S 1 X 1 S 0 Goto Table terminals and $ s t a t e s four different actions non-terminal s t a t e s each item is a state number 127
 A Configuration of LR Parsing Algorithm • A configuration of a LR parsing is: ( So X 1 S 1. . . Xm Sm, ai ai+1. . . an $ ) Stack Rest of Input • Sm and ai decides the parser action by consulting the parsing action table. (Initial Stack contains just So ) • A configuration of a LR parsing represents the right sentential form: X 1. . . Xm ai ai+1. . . an $ 128
A Configuration of LR Parsing Algorithm • A configuration of a LR parsing is: ( So X 1 S 1. . . Xm Sm, ai ai+1. . . an $ ) Stack Rest of Input • Sm and ai decides the parser action by consulting the parsing action table. (Initial Stack contains just So ) • A configuration of a LR parsing represents the right sentential form: X 1. . . Xm ai ai+1. . . an $ 128
 Actions of A LR-Parser 1. shift s -- shifts the next input symbol and the state s onto the stack ( So X 1 S 1. . . Xm Sm, ai ai+1. . . an $ ) ( So X 1 S 1. . . Xm Sm ai s, ai+1. . . an $ ) 2. reduce A (or rn where n is a production number) – pop 2| | (=r) items from the stack; – then push A and s where s=goto[sm-r, A] ( So X 1 S 1. . . Xm Sm, ai ai+1. . . an $ ) ( So X 1 S 1. . . Xm-r Sm-r A s, ai. . . an $ ) – Output is the reducing production reduce A 3. Accept – Parsing successfully completed 4. Error -- Parser detected an error (an empty entry in the action table) 129
Actions of A LR-Parser 1. shift s -- shifts the next input symbol and the state s onto the stack ( So X 1 S 1. . . Xm Sm, ai ai+1. . . an $ ) ( So X 1 S 1. . . Xm Sm ai s, ai+1. . . an $ ) 2. reduce A (or rn where n is a production number) – pop 2| | (=r) items from the stack; – then push A and s where s=goto[sm-r, A] ( So X 1 S 1. . . Xm Sm, ai ai+1. . . an $ ) ( So X 1 S 1. . . Xm-r Sm-r A s, ai. . . an $ ) – Output is the reducing production reduce A 3. Accept – Parsing successfully completed 4. Error -- Parser detected an error (an empty entry in the action table) 129
 Reduce Action • pop 2| | (=r) items from the stack; let us assume that = Y 1 Y 2. . . Yr • then push A and s where s=goto[sm-r, A] ( So X 1 S 1. . . Xm-r Sm-r Y 1 Sm-r. . . Yr Sm, ai ai+1. . . an $ ) ( So X 1 S 1. . . Xm-r Sm-r A s, ai. . . an $ ) • In fact, Y 1 Y 2. . . Yr is a handle. X 1. . . Xm-r A ai. . . an $ X 1. . . Xm Y 1. . . Yr ai ai+1. . . an $ 130
Reduce Action • pop 2| | (=r) items from the stack; let us assume that = Y 1 Y 2. . . Yr • then push A and s where s=goto[sm-r, A] ( So X 1 S 1. . . Xm-r Sm-r Y 1 Sm-r. . . Yr Sm, ai ai+1. . . an $ ) ( So X 1 S 1. . . Xm-r Sm-r A s, ai. . . an $ ) • In fact, Y 1 Y 2. . . Yr is a handle. X 1. . . Xm-r A ai. . . an $ X 1. . . Xm Y 1. . . Yr ai ai+1. . . an $ 130
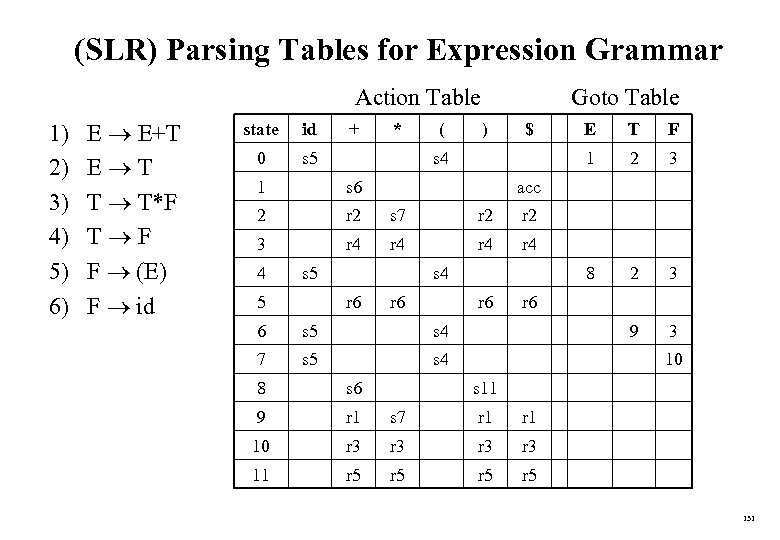 (SLR) Parsing Tables for Expression Grammar Action Table 1) 2) 3) 4) 5) 6) E E+T E T T T*F T F F (E) F id state id 0 + * s 5 ( Goto Table ) $ 2 r 2 s 7 r 2 r 4 r 4 3 2 3 3 r 2 3 2 9 s 6 F 8 1 T 1 s 4 E r 4 4 acc s 5 5 s 4 r 6 r 6 6 s 5 s 4 7 s 5 r 6 s 4 10 8 s 6 s 11 9 r 1 s 7 r 1 10 r 3 r 3 11 r 5 r 5 131
(SLR) Parsing Tables for Expression Grammar Action Table 1) 2) 3) 4) 5) 6) E E+T E T T T*F T F F (E) F id state id 0 + * s 5 ( Goto Table ) $ 2 r 2 s 7 r 2 r 4 r 4 3 2 3 3 r 2 3 2 9 s 6 F 8 1 T 1 s 4 E r 4 4 acc s 5 5 s 4 r 6 r 6 6 s 5 s 4 7 s 5 r 6 s 4 10 8 s 6 s 11 9 r 1 s 7 r 1 10 r 3 r 3 11 r 5 r 5 131
 Actions of A (S)LR-Parser -- Example stack 0 0 id 5 0 F 3 0 T 2*7 id 5 0 T 2*7 F 10 0 T 2 0 E 1+6 id 5 0 E 1+6 F 3 0 E 1+6 T 9 0 E 1 input id*id+id$ id+id$ +id$ $ $ action shift 5 reduce by F id reduce by T F shift 7 shift 5 reduce by F id reduce by T T*F reduce by E T shift 6 shift 5 reduce by F id reduce by T F reduce by E E+T accept output F id T F F id T T*F E T F id T F E E+T 132
Actions of A (S)LR-Parser -- Example stack 0 0 id 5 0 F 3 0 T 2*7 id 5 0 T 2*7 F 10 0 T 2 0 E 1+6 id 5 0 E 1+6 F 3 0 E 1+6 T 9 0 E 1 input id*id+id$ id+id$ +id$ $ $ action shift 5 reduce by F id reduce by T F shift 7 shift 5 reduce by F id reduce by T T*F reduce by E T shift 6 shift 5 reduce by F id reduce by T F reduce by E E+T accept output F id T F F id T T*F E T F id T F E E+T 132
 Constructing SLR Parsing Tables – LR(0) Item • An LR(0) item of a grammar G is a production of G a dot at the some position of the right side. • Ex: A a. Bb Possible LR(0) Items: A a. Bb (four different possibility) A a Bb A a. Bb • Sets of LR(0) items will be the states of action and goto table of the SLR parser. • A collection of sets of LR(0) items (the canonical LR(0) collection) is the basis for constructing SLR parsers. • Augmented Grammar: G’ is G with a new production rule S’ S where S’ is the new starting symbol. . . 133
Constructing SLR Parsing Tables – LR(0) Item • An LR(0) item of a grammar G is a production of G a dot at the some position of the right side. • Ex: A a. Bb Possible LR(0) Items: A a. Bb (four different possibility) A a Bb A a. Bb • Sets of LR(0) items will be the states of action and goto table of the SLR parser. • A collection of sets of LR(0) items (the canonical LR(0) collection) is the basis for constructing SLR parsers. • Augmented Grammar: G’ is G with a new production rule S’ S where S’ is the new starting symbol. . . 133
 The Closure Operation • If I is a set of LR(0) items for a grammar G, then closure(I) is the set of LR(0) items constructed from I by the two rules: . . 1. Initially, every LR(0) item in I is added to closure(I). 2. If A B is in closure(I) and B is a production rule of G; then B will be in the closure(I). We will apply this rule until no more new LR(0) items can be added to closure(I). 134
The Closure Operation • If I is a set of LR(0) items for a grammar G, then closure(I) is the set of LR(0) items constructed from I by the two rules: . . 1. Initially, every LR(0) item in I is added to closure(I). 2. If A B is in closure(I) and B is a production rule of G; then B will be in the closure(I). We will apply this rule until no more new LR(0) items can be added to closure(I). 134
 The Closure Operation -- Example E’ E E E+T E T T T*F T F F (E) F id . closure({E’ E}) = { E’ E E E+T E T T T*F T F F (E) F id } . . . . kernel items 135
The Closure Operation -- Example E’ E E E+T E T T T*F T F F (E) F id . closure({E’ E}) = { E’ E E E+T E T T T*F T F F (E) F id } . . . . kernel items 135
 Goto Operation • If I is a set of LR(0) items and X is a grammar symbol (terminal or nonterminal), then goto(I, X) is defined as follows: – If A X in I then every item in closure({A X }) will be in goto(I, X). . Example: . . I ={ E’ E, E E+T, E T, T T*F, T F, F (E), F id } goto(I, E) = { E’ E , E E +T } goto(I, T) = { E T , T T *F } goto(I, F) = {T F } goto(I, () = { F ( E), E E+T, E F (E), F id } goto(I, id) = { F id } T, T T*F, T . F, 136
Goto Operation • If I is a set of LR(0) items and X is a grammar symbol (terminal or nonterminal), then goto(I, X) is defined as follows: – If A X in I then every item in closure({A X }) will be in goto(I, X). . Example: . . I ={ E’ E, E E+T, E T, T T*F, T F, F (E), F id } goto(I, E) = { E’ E , E E +T } goto(I, T) = { E T , T T *F } goto(I, F) = {T F } goto(I, () = { F ( E), E E+T, E F (E), F id } goto(I, id) = { F id } T, T T*F, T . F, 136
 Construction of The Canonical LR(0) Collection • To create the SLR parsing tables for a grammar G, we will create the canonical LR(0) collection of the grammar G’. • Algorithm: . C is { closure({S’ S}) } repeat the followings until no more set of LR(0) items can be added to C. for each I in C and each grammar symbol X if goto(I, X) is not empty and not in C add goto(I, X) to C • goto function is a DFA on the sets in C. 137
Construction of The Canonical LR(0) Collection • To create the SLR parsing tables for a grammar G, we will create the canonical LR(0) collection of the grammar G’. • Algorithm: . C is { closure({S’ S}) } repeat the followings until no more set of LR(0) items can be added to C. for each I in C and each grammar symbol X if goto(I, X) is not empty and not in C add goto(I, X) to C • goto function is a DFA on the sets in C. 137
 The Canonical LR(0) Collection -- Example I 0: E’ . E E . E+T E . T T . T*F T . F F . (E) F . id I 1: E’ E. E E. +T I 2: E T. T T. *F I 3: T F. I 4: F (. E) E . E+T E . T T . T*F T . F F . (E) F . id I 6: E E+. T T . T*F T . F F . (E) F . id I 7: T T*. F F . (E) F . id I 9: E E+T. T T. *F I 10: T T*F. I 11: F (E). I 8: F (E. ) E E. +T I 5: F id. 138
The Canonical LR(0) Collection -- Example I 0: E’ . E E . E+T E . T T . T*F T . F F . (E) F . id I 1: E’ E. E E. +T I 2: E T. T T. *F I 3: T F. I 4: F (. E) E . E+T E . T T . T*F T . F F . (E) F . id I 6: E E+. T T . T*F T . F F . (E) F . id I 7: T T*. F F . (E) F . id I 9: E E+T. T T. *F I 10: T T*F. I 11: F (E). I 8: F (E. ) E E. +T I 5: F id. 138
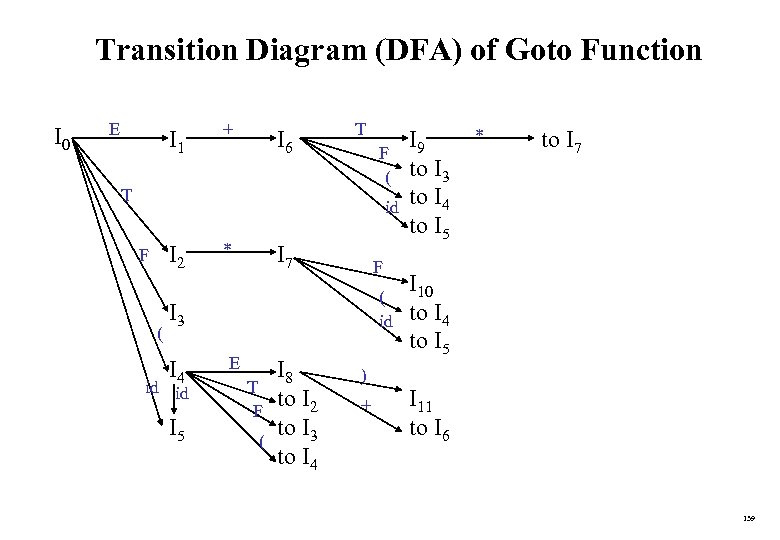 Transition Diagram (DFA) of Goto Function I 0 E I 1 + I 6 T F ( T id I 2 F ( * I 7 F ( id I 3 I 4 id id I 5 E T F ( I 8 to I 2 to I 3 to I 4 ) + I 9 to I 3 to I 4 to I 5 * to I 7 I 10 to I 4 to I 5 I 11 to I 6 139
Transition Diagram (DFA) of Goto Function I 0 E I 1 + I 6 T F ( T id I 2 F ( * I 7 F ( id I 3 I 4 id id I 5 E T F ( I 8 to I 2 to I 3 to I 4 ) + I 9 to I 3 to I 4 to I 5 * to I 7 I 10 to I 4 to I 5 I 11 to I 6 139
 Constructing SLR Parsing Table (of an augumented grammar G’) 1. Construct the canonical collection of sets of LR(0) items for G’. C {I 0, . . . , In} 2. Create the parsing action table as follows • If a is a terminal, A . a in Ii and goto(Ii, a)=Ij then action[i, a] is shift j. • If A . is in Ii , then action[i, a] is reduce A for all a in FOLLOW(A) where A S’. • If S’ S. is in Ii , then action[i, $] is accept. • If any conflicting actions generated by these rules, the grammar is not SLR(1). 3. Create the parsing goto table • for all non-terminals A, if goto(Ii, A)=Ij then goto[i, A]=j 4. All entries not defined by (2) and (3) are errors. 5. Initial state of the parser contains S’. S 140
Constructing SLR Parsing Table (of an augumented grammar G’) 1. Construct the canonical collection of sets of LR(0) items for G’. C {I 0, . . . , In} 2. Create the parsing action table as follows • If a is a terminal, A . a in Ii and goto(Ii, a)=Ij then action[i, a] is shift j. • If A . is in Ii , then action[i, a] is reduce A for all a in FOLLOW(A) where A S’. • If S’ S. is in Ii , then action[i, $] is accept. • If any conflicting actions generated by these rules, the grammar is not SLR(1). 3. Create the parsing goto table • for all non-terminals A, if goto(Ii, A)=Ij then goto[i, A]=j 4. All entries not defined by (2) and (3) are errors. 5. Initial state of the parser contains S’. S 140
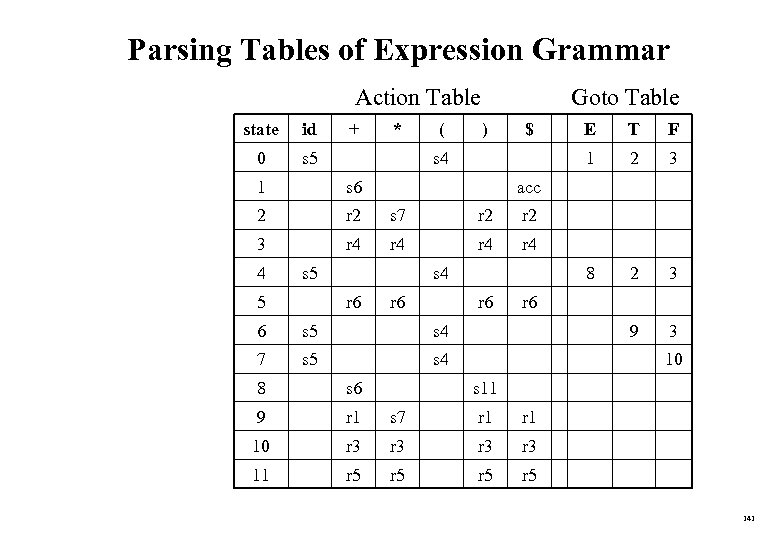 Parsing Tables of Expression Grammar Action Table state id 0 + * s 5 ( Goto Table ) $ 2 r 2 s 7 r 2 r 4 r 4 3 2 3 3 r 2 3 2 9 s 6 F 8 1 T 1 s 4 E r 4 4 acc s 5 5 s 4 r 6 r 6 6 s 5 s 4 7 s 5 r 6 s 4 10 8 s 6 s 11 9 r 1 s 7 r 1 10 r 3 r 3 11 r 5 r 5 141
Parsing Tables of Expression Grammar Action Table state id 0 + * s 5 ( Goto Table ) $ 2 r 2 s 7 r 2 r 4 r 4 3 2 3 3 r 2 3 2 9 s 6 F 8 1 T 1 s 4 E r 4 4 acc s 5 5 s 4 r 6 r 6 6 s 5 s 4 7 s 5 r 6 s 4 10 8 s 6 s 11 9 r 1 s 7 r 1 10 r 3 r 3 11 r 5 r 5 141
 SLR(1) Grammar • An LR parser using SLR(1) parsing tables for a grammar G is called as the SLR(1) parser for G. • If a grammar G has an SLR(1) parsing table, it is called SLR(1) grammar (or SLR grammar in short). • Every SLR grammar is unambiguous, but every unambiguous grammar is not a SLR grammar. 142
SLR(1) Grammar • An LR parser using SLR(1) parsing tables for a grammar G is called as the SLR(1) parser for G. • If a grammar G has an SLR(1) parsing table, it is called SLR(1) grammar (or SLR grammar in short). • Every SLR grammar is unambiguous, but every unambiguous grammar is not a SLR grammar. 142
 shift/reduce and reduce/reduce conflicts • If a state does not know whether it will make a shift operation or reduction for a terminal, we say that there is a shift/reduce conflict. • If a state does not know whether it will make a reduction operation using the production rule i or j for a terminal, we say that there is a reduce/reduce conflict. • If the SLR parsing table of a grammar G has a conflict, we say that grammar is not SLR grammar. 143
shift/reduce and reduce/reduce conflicts • If a state does not know whether it will make a shift operation or reduction for a terminal, we say that there is a shift/reduce conflict. • If a state does not know whether it will make a reduction operation using the production rule i or j for a terminal, we say that there is a reduce/reduce conflict. • If the SLR parsing table of a grammar G has a conflict, we say that grammar is not SLR grammar. 143
 Conflict Example S L=R S R L *R L id R L I 0: S’ . S S . L=R S . R L . *R L . id R . L Problem FOLLOW(R)={=, $} = shift 6 reduce by R L shift/reduce conflict I 1: S’ S. I 2: S L. =R R L. I 6: S L=. R R . L L . *R L . id I 9: S L=R. I 3: S R. I 4: L *. R R . L L . *R L . id I 7: L *R. I 8: R L. I 5: L id. 144
Conflict Example S L=R S R L *R L id R L I 0: S’ . S S . L=R S . R L . *R L . id R . L Problem FOLLOW(R)={=, $} = shift 6 reduce by R L shift/reduce conflict I 1: S’ S. I 2: S L. =R R L. I 6: S L=. R R . L L . *R L . id I 9: S L=R. I 3: S R. I 4: L *. R R . L L . *R L . id I 7: L *R. I 8: R L. I 5: L id. 144
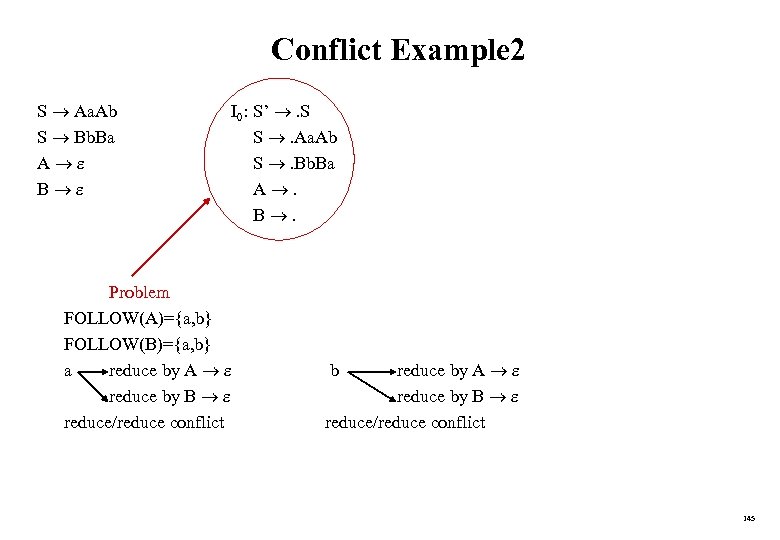 Conflict Example 2 S Aa. Ab S Bb. Ba A B I 0: S’ . S S . Aa. Ab S . Bb. Ba A. B. Problem FOLLOW(A)={a, b} FOLLOW(B)={a, b} a reduce by A reduce by B reduce/reduce conflict b 145
Conflict Example 2 S Aa. Ab S Bb. Ba A B I 0: S’ . S S . Aa. Ab S . Bb. Ba A. B. Problem FOLLOW(A)={a, b} FOLLOW(B)={a, b} a reduce by A reduce by B reduce/reduce conflict b 145
 Constructing Canonical LR(1) Parsing Tables • In SLR method, the state i makes a reduction by A when the current token is a: – if the A . in the Ii and a is FOLLOW(A) • In some situations, A cannot be followed by the terminal a in a right-sentential form when and the state i are on the top stack. This means that making reduction in this case is not correct. S Aa. Ab S Bb. Ba A B S Aa. Ab Aab ab S Bb. Ba Bba ba Aab ab Aa. Ab Aa b Bba ba Bb. Ba Bb a 146
Constructing Canonical LR(1) Parsing Tables • In SLR method, the state i makes a reduction by A when the current token is a: – if the A . in the Ii and a is FOLLOW(A) • In some situations, A cannot be followed by the terminal a in a right-sentential form when and the state i are on the top stack. This means that making reduction in this case is not correct. S Aa. Ab S Bb. Ba A B S Aa. Ab Aab ab S Bb. Ba Bba ba Aab ab Aa. Ab Aa b Bba ba Bb. Ba Bb a 146
 LR(1) Item • To avoid some of invalid reductions, the states need to carry more information. • Extra information is put into a state by including a terminal symbol as a second component in an item. • A LR(1) item is: . A , a where a is the look-head of the LR(1) item (a is a terminal or end-marker. ) 147
LR(1) Item • To avoid some of invalid reductions, the states need to carry more information. • Extra information is put into a state by including a terminal symbol as a second component in an item. • A LR(1) item is: . A , a where a is the look-head of the LR(1) item (a is a terminal or end-marker. ) 147
 LR(1) Item (cont. ) . • When ( in the LR(1) item A , a ) is not empty, the look-head does not have any affect. . • When is empty (A , a ), we do the reduction by A only if the next input symbol is a (not for any terminal in FOLLOW(A)). . • A state will contain A , a 1 where {a 1, . . . , an} FOLLOW(A). . A , an 148
LR(1) Item (cont. ) . • When ( in the LR(1) item A , a ) is not empty, the look-head does not have any affect. . • When is empty (A , a ), we do the reduction by A only if the next input symbol is a (not for any terminal in FOLLOW(A)). . • A state will contain A , a 1 where {a 1, . . . , an} FOLLOW(A). . A , an 148
 Canonical Collection of Sets of LR(1) Items • The construction of the canonical collection of the sets of LR(1) items are similar to the construction of the canonical collection of the sets of LR(0) items, except that closure and goto operations work a little bit different. closure(I) is: ( where I is a set of LR(1) items) – every LR(1) item in I is in closure(I) . – if A B , a in closure(I) and B is a production rule of G; then B. , b will be in the closure(I) for each terminal b in FIRST( a). 149
Canonical Collection of Sets of LR(1) Items • The construction of the canonical collection of the sets of LR(1) items are similar to the construction of the canonical collection of the sets of LR(0) items, except that closure and goto operations work a little bit different. closure(I) is: ( where I is a set of LR(1) items) – every LR(1) item in I is in closure(I) . – if A B , a in closure(I) and B is a production rule of G; then B. , b will be in the closure(I) for each terminal b in FIRST( a). 149
 goto operation • If I is a set of LR(1) items and X is a grammar symbol (terminal or non-terminal), then goto(I, X) is defined as follows: – If A . X , a in I then every item in closure({A X. , a}) will be in goto(I, X). 150
goto operation • If I is a set of LR(1) items and X is a grammar symbol (terminal or non-terminal), then goto(I, X) is defined as follows: – If A . X , a in I then every item in closure({A X. , a}) will be in goto(I, X). 150
 Construction of The Canonical LR(1) Collection • Algorithm: C is { closure({S’. S, $}) } repeat the followings until no more set of LR(1) items can be added to C. for each I in C and each grammar symbol X if goto(I, X) is not empty and not in C add goto(I, X) to C • goto function is a DFA on the sets in C. 151
Construction of The Canonical LR(1) Collection • Algorithm: C is { closure({S’. S, $}) } repeat the followings until no more set of LR(1) items can be added to C. for each I in C and each grammar symbol X if goto(I, X) is not empty and not in C add goto(I, X) to C • goto function is a DFA on the sets in C. 151
 A Short Notation for The Sets of LR(1) Items • A set of LR(1) items containing the following items . A , a 1. . A , an can be written as . A , a 1/a 2/. . . /an 152
A Short Notation for The Sets of LR(1) Items • A set of LR(1) items containing the following items . A , a 1. . A , an can be written as . A , a 1/a 2/. . . /an 152
 Canonical LR(1) Collection -- Example S Aa. Ab S Bb. Ba A B I 0: S’ . S , $ S . Aa. Ab , $ S . Bb. Ba , $ A . , a B . , b I 1: S’ S. , $ S A a I 3: S B. b. Ba , $ B I 2: S A. a. Ab , $ b I 4: S Aa. Ab , $ A . , b A I 6: S Aa. A. b , $ a B I 7: S Bb. B. a , $ b to I 5 I 8: S Aa. Ab. , $ I 5: S Bb. Ba , $ B . , a to I 4 I 9: S Bb. Ba. , $ 153
Canonical LR(1) Collection -- Example S Aa. Ab S Bb. Ba A B I 0: S’ . S , $ S . Aa. Ab , $ S . Bb. Ba , $ A . , a B . , b I 1: S’ S. , $ S A a I 3: S B. b. Ba , $ B I 2: S A. a. Ab , $ b I 4: S Aa. Ab , $ A . , b A I 6: S Aa. A. b , $ a B I 7: S Bb. B. a , $ b to I 5 I 8: S Aa. Ab. , $ I 5: S Bb. Ba , $ B . , a to I 4 I 9: S Bb. Ba. , $ 153
 Canonical LR(1) Collection – Example 2 S’ S 1) S L=R 2) S R 3) L *R 4) L id 5) R L I 0: S’ . S, $ S . L=R, $ S . R, $ L . *R, $/= L . id, $/= R . L, $ I 6: S L=. R, $ R . L, $ L . *R, $ L . id, $ R L * I 1: S’ S. , $ S * L I 2: S L. =R, $ R L. , $ R I 3: S R. , $ id to I 9 to I 10 to I 11 I 8: R L. , $/= I 12: L id. , $ to I 7 L * to I 8 id to I 4 to I 5 I 13: L *R. , $ I 10: R L. , $ I 7: L *R. , $/= to I 12 R I 5: L id. , $/= I 9: S L=R. , $ I 11: L *. R, $ R . L, $ L . *R, $ L . id, $ id I 4: L *. R, $/= R . L, $/= to I 6 L . *R, $/= L . id, $/= I 4 and I 11 R L * id to I 13 to I 10 I 5 and I 12 to I 11 I 7 and I 13 to I 12 I 8 and I 10 154
Canonical LR(1) Collection – Example 2 S’ S 1) S L=R 2) S R 3) L *R 4) L id 5) R L I 0: S’ . S, $ S . L=R, $ S . R, $ L . *R, $/= L . id, $/= R . L, $ I 6: S L=. R, $ R . L, $ L . *R, $ L . id, $ R L * I 1: S’ S. , $ S * L I 2: S L. =R, $ R L. , $ R I 3: S R. , $ id to I 9 to I 10 to I 11 I 8: R L. , $/= I 12: L id. , $ to I 7 L * to I 8 id to I 4 to I 5 I 13: L *R. , $ I 10: R L. , $ I 7: L *R. , $/= to I 12 R I 5: L id. , $/= I 9: S L=R. , $ I 11: L *. R, $ R . L, $ L . *R, $ L . id, $ id I 4: L *. R, $/= R . L, $/= to I 6 L . *R, $/= L . id, $/= I 4 and I 11 R L * id to I 13 to I 10 I 5 and I 12 to I 11 I 7 and I 13 to I 12 I 8 and I 10 154
 Construction of LR(1) Parsing Tables 1. Construct the canonical collection of sets of LR(1) items for G’. C {I 0, . . . , In} 2. Create the parsing action table as follows • • . If a is a terminal, A a , b in Ii and goto(Ii, a)=Ij then action[i, a] is shift j. If A , a is in Ii , then action[i, a] is reduce A where A S’. If S’ S , $ is in Ii , then action[i, $] is accept. If any conflicting actions generated by these rules, the grammar is not LR(1). . . 3. Create the parsing goto table • for all non-terminals A, if goto(Ii, A)=Ij then goto[i, A]=j 4. All entries not defined by (2) and (3) are errors. 5. Initial state of the parser contains S’. S, $ 155
Construction of LR(1) Parsing Tables 1. Construct the canonical collection of sets of LR(1) items for G’. C {I 0, . . . , In} 2. Create the parsing action table as follows • • . If a is a terminal, A a , b in Ii and goto(Ii, a)=Ij then action[i, a] is shift j. If A , a is in Ii , then action[i, a] is reduce A where A S’. If S’ S , $ is in Ii , then action[i, $] is accept. If any conflicting actions generated by these rules, the grammar is not LR(1). . . 3. Create the parsing goto table • for all non-terminals A, if goto(Ii, A)=Ij then goto[i, A]=j 4. All entries not defined by (2) and (3) are errors. 5. Initial state of the parser contains S’. S, $ 155
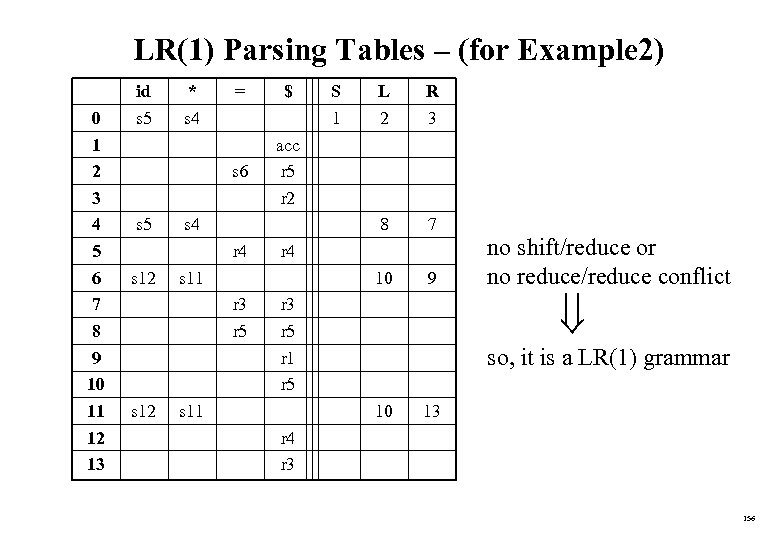 LR(1) Parsing Tables – (for Example 2) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 id s 5 = $ s 6 s 5 * s 4 acc r 5 r 2 s 12 7 9 r 4 s 11 r 3 r 5 R 3 10 r 4 L 2 8 s 4 S 1 r 3 r 5 r 1 r 5 s 11 no shift/reduce or no reduce/reduce conflict so, it is a LR(1) grammar 10 13 r 4 r 3 156
LR(1) Parsing Tables – (for Example 2) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 id s 5 = $ s 6 s 5 * s 4 acc r 5 r 2 s 12 7 9 r 4 s 11 r 3 r 5 R 3 10 r 4 L 2 8 s 4 S 1 r 3 r 5 r 1 r 5 s 11 no shift/reduce or no reduce/reduce conflict so, it is a LR(1) grammar 10 13 r 4 r 3 156
 LALR Parsing Tables • LALR stands for Look. Ahead LR. • LALR parsers are often used in practice because LALR parsing tables are smaller than LR(1) parsing tables. • The number of states in SLR and LALR parsing tables for a grammar G are equal. • But LALR parsers recognize more grammars than SLR parsers. • yacc creates a LALR parser for the given grammar. • A state of LALR parser will be again a set of LR(1) items. 157
LALR Parsing Tables • LALR stands for Look. Ahead LR. • LALR parsers are often used in practice because LALR parsing tables are smaller than LR(1) parsing tables. • The number of states in SLR and LALR parsing tables for a grammar G are equal. • But LALR parsers recognize more grammars than SLR parsers. • yacc creates a LALR parser for the given grammar. • A state of LALR parser will be again a set of LR(1) items. 157
 Creating LALR Parsing Tables Canonical LR(1) Parser shrink # of states LALR Parser • This shrink process may introduce a reduce/reduce conflict in the resulting LALR parser (so the grammar is NOT LALR) • But, this shrink process does not produce a shift/reduce conflict. 158
Creating LALR Parsing Tables Canonical LR(1) Parser shrink # of states LALR Parser • This shrink process may introduce a reduce/reduce conflict in the resulting LALR parser (so the grammar is NOT LALR) • But, this shrink process does not produce a shift/reduce conflict. 158
 The Core of A Set of LR(1) Items • The core of a set of LR(1) items is the set of its first component. Ex: . . S L =R, $ R L , $ . . S L =R R L Core • We will find the states (sets of LR(1) items) in a canonical LR(1) parser with same cores. Then we will merge them as a single state. . . I 1: L id , = I 2: L id , $ A new state: . . I 12: L id , = L id , $ have same core, merge them • We will do this for all states of a canonical LR(1) parser to get the states of the LALR parser. • In fact, the number of the states of the LALR parser for a grammar will be equal to the number of states of the SLR parser for that grammar. 159
The Core of A Set of LR(1) Items • The core of a set of LR(1) items is the set of its first component. Ex: . . S L =R, $ R L , $ . . S L =R R L Core • We will find the states (sets of LR(1) items) in a canonical LR(1) parser with same cores. Then we will merge them as a single state. . . I 1: L id , = I 2: L id , $ A new state: . . I 12: L id , = L id , $ have same core, merge them • We will do this for all states of a canonical LR(1) parser to get the states of the LALR parser. • In fact, the number of the states of the LALR parser for a grammar will be equal to the number of states of the SLR parser for that grammar. 159
 Creation of LALR Parsing Tables • Create the canonical LR(1) collection of the sets of LR(1) items for the given grammar. • Find each core; find all sets having that same core; replace those sets having same cores with a single set which is their union. C={I 0, . . . , In} C’={J 1, . . . , Jm} where m n • Create the parsing tables (action and goto tables) same as the construction of the parsing tables of LR(1) parser. – Note that: If J=I 1 . . . Ik since I 1, . . . , Ik have same cores of goto(I 1, X), . . . , goto(I 2, X) must be same. – So, goto(J, X)=K where K is the union of all sets of items having same cores as goto(I 1, X). • If no conflict is introduced, the grammar is LALR(1) grammar. (We may only introduce reduce/reduce conflicts; we cannot introduce a shift/reduce conflict) 160
Creation of LALR Parsing Tables • Create the canonical LR(1) collection of the sets of LR(1) items for the given grammar. • Find each core; find all sets having that same core; replace those sets having same cores with a single set which is their union. C={I 0, . . . , In} C’={J 1, . . . , Jm} where m n • Create the parsing tables (action and goto tables) same as the construction of the parsing tables of LR(1) parser. – Note that: If J=I 1 . . . Ik since I 1, . . . , Ik have same cores of goto(I 1, X), . . . , goto(I 2, X) must be same. – So, goto(J, X)=K where K is the union of all sets of items having same cores as goto(I 1, X). • If no conflict is introduced, the grammar is LALR(1) grammar. (We may only introduce reduce/reduce conflicts; we cannot introduce a shift/reduce conflict) 160
 Shift/Reduce Conflict • We say that we cannot introduce a shift/reduce conflict during the shrink process for the creation of the states of a LALR parser. • Assume that we can introduce a shift/reduce conflict. In this case, a state of LALR parser must have: . . A , a and B a , b • This means that a state of the canonical LR(1) parser must have: A , a and B a , c But, this state has also a shift/reduce conflict. i. e. The original canonical LR(1) parser has a conflict. (Reason for this, the shift operation does not depend on lookaheads) 161
Shift/Reduce Conflict • We say that we cannot introduce a shift/reduce conflict during the shrink process for the creation of the states of a LALR parser. • Assume that we can introduce a shift/reduce conflict. In this case, a state of LALR parser must have: . . A , a and B a , b • This means that a state of the canonical LR(1) parser must have: A , a and B a , c But, this state has also a shift/reduce conflict. i. e. The original canonical LR(1) parser has a conflict. (Reason for this, the shift operation does not depend on lookaheads) 161
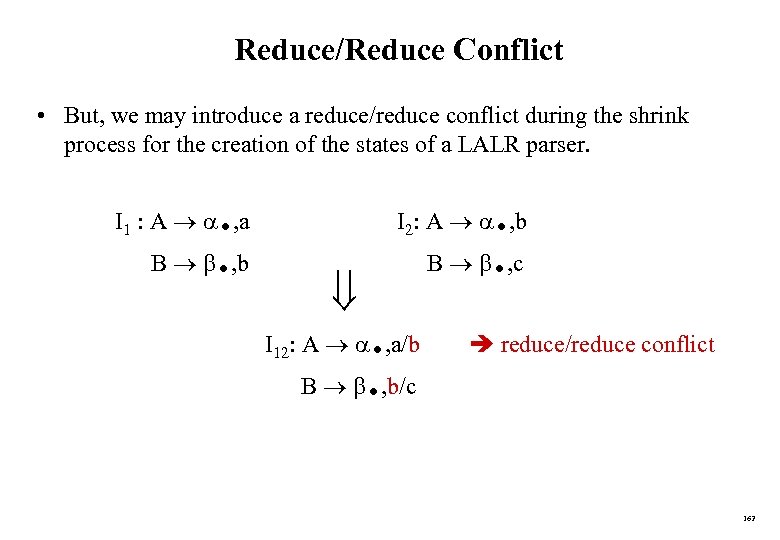 Reduce/Reduce Conflict • But, we may introduce a reduce/reduce conflict during the shrink process for the creation of the states of a LALR parser. . . I 1 : A , a I 2: A , b B , c . . I 12: A , a/b reduce/reduce conflict B , b/c 162
Reduce/Reduce Conflict • But, we may introduce a reduce/reduce conflict during the shrink process for the creation of the states of a LALR parser. . . I 1 : A , a I 2: A , b B , c . . I 12: A , a/b reduce/reduce conflict B , b/c 162
 Canonical LALR(1) Collection – Example 2 S’ S 1) S L=R 2) S R 3) L *R 4) L id 5) R L . . . I 0: S’ S S L L R I 6: S L= R, $ R L, $ L *R, $ L id, $ I 713: L *R , $/= I 810: R L , $/= R L * id S, $ L=R, $ *R, $/= id, $/= L, $ to I 9 to I 810 to I 411 to I 512 . . I 1: S’ S , $ I 411: L * R, $/= S * R L, $/= L I 2: S L =R, $ to I 6 L *R, $/= R L , $ L id, $/= R id I 3: S R , $ I : L id , $/= 512 . I 9: S L=R , $ R to I 713 L * to I 810 id to I 411 to I 512 Same Cores I 4 and I 11 I 5 and I 12 I 7 and I 13 I 8 and I 10 163
Canonical LALR(1) Collection – Example 2 S’ S 1) S L=R 2) S R 3) L *R 4) L id 5) R L . . . I 0: S’ S S L L R I 6: S L= R, $ R L, $ L *R, $ L id, $ I 713: L *R , $/= I 810: R L , $/= R L * id S, $ L=R, $ *R, $/= id, $/= L, $ to I 9 to I 810 to I 411 to I 512 . . I 1: S’ S , $ I 411: L * R, $/= S * R L, $/= L I 2: S L =R, $ to I 6 L *R, $/= R L , $ L id, $/= R id I 3: S R , $ I : L id , $/= 512 . I 9: S L=R , $ R to I 713 L * to I 810 id to I 411 to I 512 Same Cores I 4 and I 11 I 5 and I 12 I 7 and I 13 I 8 and I 10 163
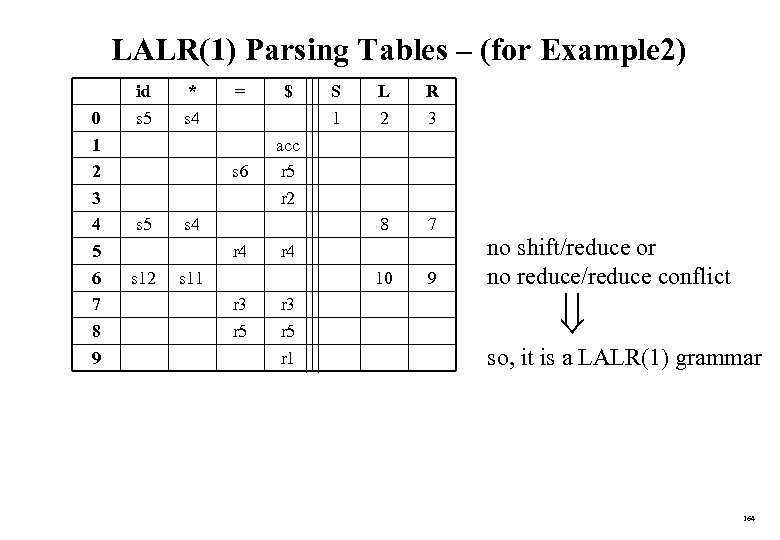 LALR(1) Parsing Tables – (for Example 2) 0 1 2 3 4 5 6 7 8 9 id s 5 = $ s 6 s 5 * s 4 acc r 5 r 2 s 12 7 9 r 4 s 11 r 3 r 5 R 3 10 r 4 L 2 8 s 4 S 1 r 3 r 5 r 1 no shift/reduce or no reduce/reduce conflict so, it is a LALR(1) grammar 164
LALR(1) Parsing Tables – (for Example 2) 0 1 2 3 4 5 6 7 8 9 id s 5 = $ s 6 s 5 * s 4 acc r 5 r 2 s 12 7 9 r 4 s 11 r 3 r 5 R 3 10 r 4 L 2 8 s 4 S 1 r 3 r 5 r 1 no shift/reduce or no reduce/reduce conflict so, it is a LALR(1) grammar 164
 Using Ambiguous Grammars • All grammars used in the construction of LR-parsing tables must be un -ambiguous. • Can we create LR-parsing tables for ambiguous grammars ? – Yes, but they will have conflicts. – We can resolve these conflicts in favor of one of them to disambiguate the grammar. – At the end, we will have again an unambiguous grammar. • Why we want to use an ambiguous grammar? – Some of the ambiguous grammars are much natural, and a corresponding unambiguous grammar can be very complex. – Usage of an ambiguous grammar may eliminate unnecessary reductions. • Ex. E E+T | T E E+E | E*E | (E) | id T T*F | F F (E) | id 165
Using Ambiguous Grammars • All grammars used in the construction of LR-parsing tables must be un -ambiguous. • Can we create LR-parsing tables for ambiguous grammars ? – Yes, but they will have conflicts. – We can resolve these conflicts in favor of one of them to disambiguate the grammar. – At the end, we will have again an unambiguous grammar. • Why we want to use an ambiguous grammar? – Some of the ambiguous grammars are much natural, and a corresponding unambiguous grammar can be very complex. – Usage of an ambiguous grammar may eliminate unnecessary reductions. • Ex. E E+T | T E E+E | E*E | (E) | id T T*F | F F (E) | id 165
 Sets of LR(0) Items for Ambiguous Grammar . E+E E. E*E. (E). id. I 0: E’ E E . . . E I 1: E’ E E E +E E E *E ( + ( . E+E E). E*E. (E). id. I 2 : E ( E E E id E I 3: E id id . . . I : E E *. E E . E+E E . E*E E . (E) E . id I 4 : E E + E E E+E E E*E * E (E) E id E ( id 5 E . . . I 6: E (E ) E E +E E E *E I 2 I 3 ( id . . . I 7: E E+E + I 4 E E +E * I 5 E E *E E I 2 I 3 ) + * I 4 I 5 . . . I 8: E E*E + I 4 E E +E * I 5 E E *E I 9: E (E) . 166
Sets of LR(0) Items for Ambiguous Grammar . E+E E. E*E. (E). id. I 0: E’ E E . . . E I 1: E’ E E E +E E E *E ( + ( . E+E E). E*E. (E). id. I 2 : E ( E E E id E I 3: E id id . . . I : E E *. E E . E+E E . E*E E . (E) E . id I 4 : E E + E E E+E E E*E * E (E) E id E ( id 5 E . . . I 6: E (E ) E E +E E E *E I 2 I 3 ( id . . . I 7: E E+E + I 4 E E +E * I 5 E E *E E I 2 I 3 ) + * I 4 I 5 . . . I 8: E E*E + I 4 E E +E * I 5 E E *E I 9: E (E) . 166
 SLR-Parsing Tables for Ambiguous Grammar FOLLOW(E) = { $, +, *, ) } State I 7 has shift/reduce conflicts for symbols + and *. I 0 E I 1 + I 4 E I 7 when current token is + shift + is right-associative reduce + is left-associative when current token is * shift * has higher precedence than + reduce + has higher precedence than * 167
SLR-Parsing Tables for Ambiguous Grammar FOLLOW(E) = { $, +, *, ) } State I 7 has shift/reduce conflicts for symbols + and *. I 0 E I 1 + I 4 E I 7 when current token is + shift + is right-associative reduce + is left-associative when current token is * shift * has higher precedence than + reduce + has higher precedence than * 167
 SLR-Parsing Tables for Ambiguous Grammar FOLLOW(E) = { $, +, *, ) } State I 8 has shift/reduce conflicts for symbols + and *. I 0 E I 1 * I 5 E I 8 when current token is * shift * is right-associative reduce * is left-associative when current token is + shift + has higher precedence than * reduce * has higher precedence than + 168
SLR-Parsing Tables for Ambiguous Grammar FOLLOW(E) = { $, +, *, ) } State I 8 has shift/reduce conflicts for symbols + and *. I 0 E I 1 * I 5 E I 8 when current token is * shift * is right-associative reduce * is left-associative when current token is + shift + has higher precedence than * reduce * has higher precedence than + 168
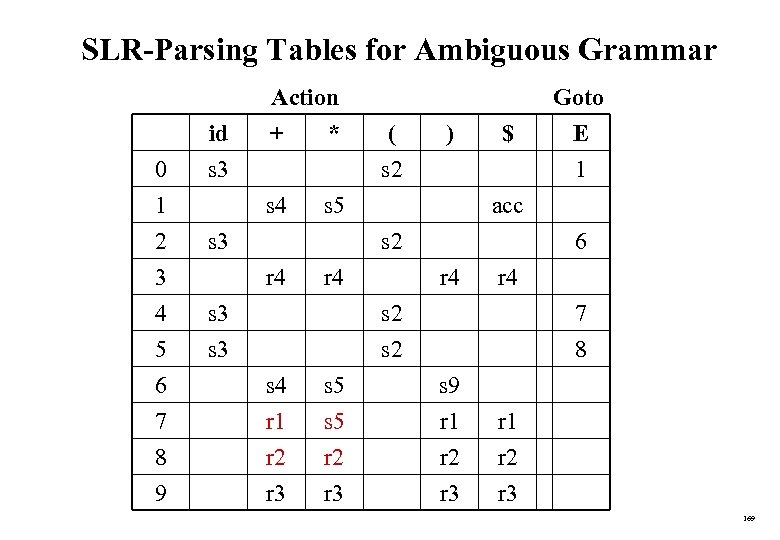 SLR-Parsing Tables for Ambiguous Grammar 0 1 2 3 4 5 6 7 8 9 id s 3 Action + * s 4 ( s 2 ) s 5 s 3 $ acc s 2 r 4 s 3 6 r 4 s 2 s 4 r 1 r 2 r 3 s 5 r 2 r 3 Goto E 1 7 8 s 9 r 1 r 2 r 3 169
SLR-Parsing Tables for Ambiguous Grammar 0 1 2 3 4 5 6 7 8 9 id s 3 Action + * s 4 ( s 2 ) s 5 s 3 $ acc s 2 r 4 s 3 6 r 4 s 2 s 4 r 1 r 2 r 3 s 5 r 2 r 3 Goto E 1 7 8 s 9 r 1 r 2 r 3 169
 Error Recovery in LR Parsing • An LR parser will detect an error when it consults the parsing action table and finds an error entry. All empty entries in the action table are error entries. • Errors are never detected by consulting the goto table. • An LR parser will announce error as soon as there is no valid continuation for the scanned portion of the input. • A canonical LR parser (LR(1) parser) will never make even a single reduction before announcing an error. • The SLR and LALR parsers may make several reductions before announcing an error. • But, all LR parsers (LR(1), LALR and SLR parsers) will never shift an erroneous input symbol onto the stack. 170
Error Recovery in LR Parsing • An LR parser will detect an error when it consults the parsing action table and finds an error entry. All empty entries in the action table are error entries. • Errors are never detected by consulting the goto table. • An LR parser will announce error as soon as there is no valid continuation for the scanned portion of the input. • A canonical LR parser (LR(1) parser) will never make even a single reduction before announcing an error. • The SLR and LALR parsers may make several reductions before announcing an error. • But, all LR parsers (LR(1), LALR and SLR parsers) will never shift an erroneous input symbol onto the stack. 170
 Panic Mode Error Recovery in LR Parsing • Scan down the stack until a state s with a goto on a particular nonterminal A is found. (Get rid of everything from the stack before this state s). • Discard zero or more input symbols until a symbol a is found that can legitimately follow A. – The symbol a is simply in FOLLOW(A), but this may not work for all situations. • The parser stacks the nonterminal A and the state goto[s, A], and it resumes the normal parsing. • This nonterminal A is normally is a basic programming block (there can be more than one choice for A). – stmt, expr, block, . . . 171
Panic Mode Error Recovery in LR Parsing • Scan down the stack until a state s with a goto on a particular nonterminal A is found. (Get rid of everything from the stack before this state s). • Discard zero or more input symbols until a symbol a is found that can legitimately follow A. – The symbol a is simply in FOLLOW(A), but this may not work for all situations. • The parser stacks the nonterminal A and the state goto[s, A], and it resumes the normal parsing. • This nonterminal A is normally is a basic programming block (there can be more than one choice for A). – stmt, expr, block, . . . 171
 Phrase-Level Error Recovery in LR Parsing • Each empty entry in the action table is marked with a specific error routine. • An error routine reflects the error that the user most likely will make in that case. • An error routine inserts the symbols into the stack or the input (or it deletes the symbols from the stack and the input, or it can do both insertion and deletion). – missing operand – unbalanced right parenthesis 172
Phrase-Level Error Recovery in LR Parsing • Each empty entry in the action table is marked with a specific error routine. • An error routine reflects the error that the user most likely will make in that case. • An error routine inserts the symbols into the stack or the input (or it deletes the symbols from the stack and the input, or it can do both insertion and deletion). – missing operand – unbalanced right parenthesis 172


