22908177e4745bdcfd32998fff02f3e9.ppt
- Количество слайдов: 67

Compilation of Socialite, Dedalus & Web. DAMLog A Spontaneous Talk Christoph Koch EPFL DATA Lab christoph. koch@epfl. ch http: //data. epfl. ch

2 This talk Warning: I decided to prepare this talk today at 1: 30 pm !!!111!!

3 Goal • Some of you know the DBToaster project: • • • Aggressive incremental view maintenance + compilation. Recently, we have made our compiled code much faster. New goal: compile languages with recursion: • • Socialite (Lam/Stanford): graph analytics Dynamic languages: Web. DAMLog, Bloom, Dedalus • But: this work is not ready. I will only sketch challenges and tell you about our status. • A talk to friends on work in progress is probably better than utterly boring them with something unrelated to this workshop.

4 Talk Overview • Classic DBToaster • The new backend: Scala & LMS • Towards a compiler for Web. DAMLog

5 Use Cases of DBToaster • Online/real-time analytics • Real-time data warehousing, network/financial policy monitoring, clickstream analysis, spyware , order-book trading, … • Stream/CEP abstractions (window semantics, “finite” automata) often not appropriate. • • Combine stream with historical data E. g. order books are not windows

Incremental View Maintenance • Given a DB update, do not recompute the view from scratch. • Perform only the work needed to update the view. • Compute delta query: • • Delta queries work on less data; also slightly simpler. But: we still need a classical query engine for processing the delta queries. [Roussopoulos, 1991; Yan and Larson, 1995; Colby et al, 1996; Kotidis and Roussopoulos, 2001; Zhou et al, 2007] CREATE MATERIALIZED VIEW empdep REFRESH FAST ON COMMIT AS SELECT empno, ename, dname FROM emp e, dept d WHERE e. deptno = d. deptno; (Example in Oracle)

Recursive incremental processing

Compiling incremental view maintenance

A ring of relations

Aggregation Calculus (AGCA)

Deltas of AGCA queries; closure AGCA is closed under taking deltas!

Degrees of deltas; high deltas are independent of the database
![Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line.](https://present5.com/presentation/22908177e4745bdcfd32998fff02f3e9/image-13.jpg)
Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Item LI where O. OK = LI. OK;
![Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line.](https://present5.com/presentation/22908177e4745bdcfd32998fff02f3e9/image-14.jpg)
Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Item LI where O. OK = LI. OK; +O(x. OK, x. CK, x. D, x. XCH) q[] += select sum(LI. P * O. XCH) from {<x. OK, x. CK, x. D, x. XCH>} O, Line. Item LI where O. OK = LI. OK; +LI(y. OK, y. P) q[] +=. . .
![Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line.](https://present5.com/presentation/22908177e4745bdcfd32998fff02f3e9/image-15.jpg)
Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Item LI where O. OK = LI. OK; +O(x. OK, x. CK, x. D, x. XCH) q[] += select sum(LI. P * x. XCH) from Line. Item LI where x. OK = LI. OK; +LI(y. OK, y. P) q[] +=. . .
![Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line.](https://present5.com/presentation/22908177e4745bdcfd32998fff02f3e9/image-16.jpg)
Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Item LI where O. OK = LI. OK; +O(x. OK, x. CK, x. D, x. XCH) q[] += x. XCH * select sum(LI. P) from Line. Item LI where x. OK = LI. OK; +LI(y. OK, y. P) q. O[x. OK] q[] +=. . .
![Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line.](https://present5.com/presentation/22908177e4745bdcfd32998fff02f3e9/image-17.jpg)
Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Item LI where O. OK = LI. OK; +O(x. OK, x. CK, x. D, x. XCH) q[] += x. XCH * q. O[x. OK]; foreach x. OK: q. O[x. OK] = select sum(LI. P) from Line. Item LI where x. OK = LI. OK; +LI(y. OK, y. P) q[] +=. . .
![Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line.](https://present5.com/presentation/22908177e4745bdcfd32998fff02f3e9/image-18.jpg)
Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Item LI where O. OK = LI. OK; +O(x. OK, x. CK, x. D, x. XCH) q[] += x. XCH * q. O[x. OK]; +LI(y. OK, y. P) foreach x. OK: q. O[x. OK] += select sum(LI. P) from {<y. OK, y. P>} LI where x. OK = LI. OK; +LI(y. OK, y. P) q[] +=. . .
![Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line.](https://present5.com/presentation/22908177e4745bdcfd32998fff02f3e9/image-19.jpg)
Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Item LI where O. OK = LI. OK; +O(x. OK, x. CK, x. D, x. XCH) q[] += x. XCH * q. O[x. OK]; +LI(y. OK, y. P) foreach x. OK: q. O[x. OK] += select y. P where x. OK = y. OK; +LI(y. OK, y. P) q[] +=. . .
![Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line.](https://present5.com/presentation/22908177e4745bdcfd32998fff02f3e9/image-20.jpg)
Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Item LI where O. OK = LI. OK; +O(x. OK, x. CK, x. D, x. XCH) q[] += x. XCH * q. O[x. OK]; +LI(y. OK, y. P) q. O[y. OK] += y. P; +LI(y. OK, y. P) q[] +=. . .
![Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line.](https://present5.com/presentation/22908177e4745bdcfd32998fff02f3e9/image-21.jpg)
Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Item LI where O. OK = LI. OK; +O(x. OK, x. CK, x. D, x. XCH) q[] += x. XCH * q. O[x. OK]; +LI(y. OK, y. P) q. O[y. OK] += y. P; +LI(y. OK, y. P) q[] += select sum(LI. P * O. XCH) from Order O, {<y. OK, y. P>} LI where O. OK = LI. OK;
![Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line.](https://present5.com/presentation/22908177e4745bdcfd32998fff02f3e9/image-22.jpg)
Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Item LI where O. OK = LI. OK; +O(x. OK, x. CK, x. D, x. XCH) q[] += x. XCH * q. O[x. OK]; +LI(y. OK, y. P) q. O[y. OK] += y. P; +LI(y. OK, y. P) q[] += select sum( y. P * O. XCH) from Order O where O. OK = y. OK;
![Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line.](https://present5.com/presentation/22908177e4745bdcfd32998fff02f3e9/image-23.jpg)
Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Item LI where O. OK = LI. OK; +O(x. OK, x. CK, x. D, x. XCH) q[] += x. XCH * q. O[x. OK]; +LI(y. OK, y. P) q. O[y. OK] += y. P; +LI(y. OK, y. P) q[] += y. P * select sum( from Order O where O. OK = O. XCH) y. OK;
![Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line.](https://present5.com/presentation/22908177e4745bdcfd32998fff02f3e9/image-24.jpg)
Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Item LI where O. OK = LI. OK; +O(x. OK, x. CK, x. D, x. XCH) q[] += x. XCH * q. O[x. OK]; +LI(y. OK, y. P) q. O[y. OK] += y. P; +LI(y. OK, y. P) q[] += y. P * q. LI[y. OK]; select sum( from Order O where O. OK = O. XCH) q. LI[y. OK] y. OK;
![Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line.](https://present5.com/presentation/22908177e4745bdcfd32998fff02f3e9/image-25.jpg)
Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Item LI where O. OK = LI. OK; +O(x. OK, x. CK, x. D, x. XCH) q[] += x. XCH * q. O[x. OK]; +LI(y. OK, y. P) q. O[y. OK] += y. P; +LI(y. OK, y. P) q[] += y. P * q. LI[y. OK]; +O(x. OK, x. CK, x. D, x. XCH) foreach y. OK: q. LI[y. OK] += select sum( O. XCH) from {<x. OK, x. CK, x. D, x. XCH>} O where O. OK = y. OK;
![Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line.](https://present5.com/presentation/22908177e4745bdcfd32998fff02f3e9/image-26.jpg)
Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Item LI where O. OK = LI. OK; +O(x. OK, x. CK, x. D, x. XCH) +LI(y. OK, y. PK, y. P) +O(x. OK, x. CK, x. D, x. XCH) select where x. OK = q[] += x. XCH * q. O[x. OK]; q. O[y. OK] += y. P; q[] += y. P * q. LI[y. OK]; foreach y. OK: q. LI[y. OK] += x. XCH y. OK;
![Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line.](https://present5.com/presentation/22908177e4745bdcfd32998fff02f3e9/image-27.jpg)
Compilation Example q[] = select sum(LI. P * O. XCH) from Order O, Line. Item LI where O. OK = LI. OK; +O(x. OK, x. CK, x. D, x. XCH) +LI(y. OK, y. PK, y. P) +O(x. OK, x. CK, x. D, x. XCH) • • q[] += x. XCH * q. O[x. OK]; q. O[y. OK] += y. P; q[] += y. P * q. LI[y. OK]; q. LI[x. OK] += x. XCH; The triggers for incrementally maintaining all the maps run in constant time! No nonincremental algorithm can do that!

Parallel complexity of compiled queries

29 The DBToaster compiler: status • We are able to maintain queries with nested aggregates! • Query optimization problem interesting • Nesting, correlated variables, maintaining their domains. • See our VLDB 2012 paper. • Scala and C code generators (Scala is faster!) • Released at www. dbtoaster. org • Three parallel runtime systems: • • Using Spark (bad), Storm/Squall (data flow parallelism), Cumulus (message passing) Released soon.
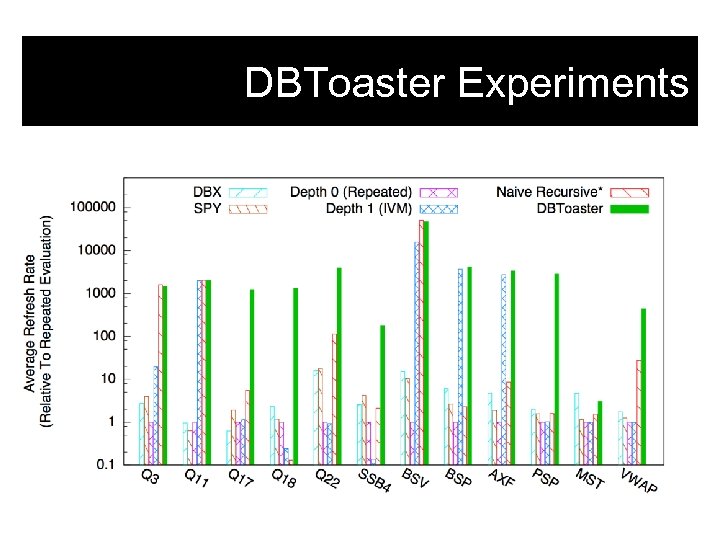
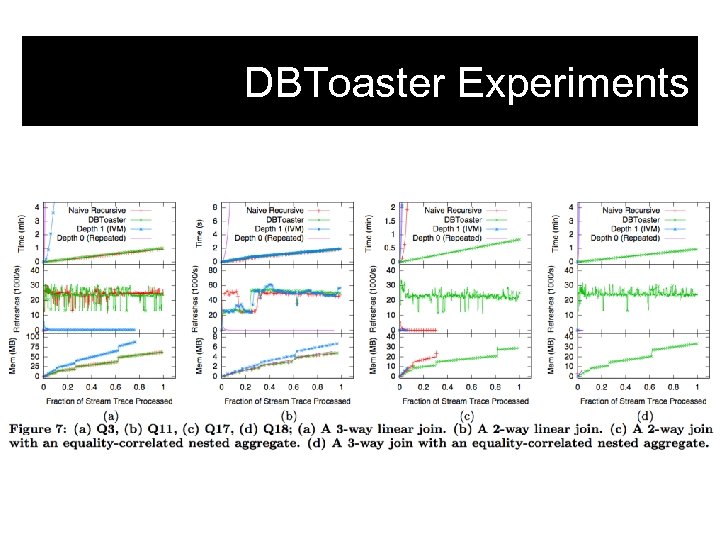
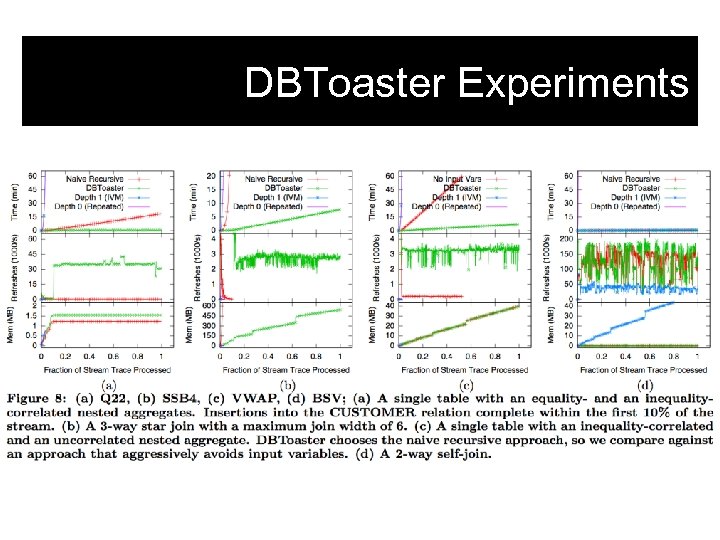
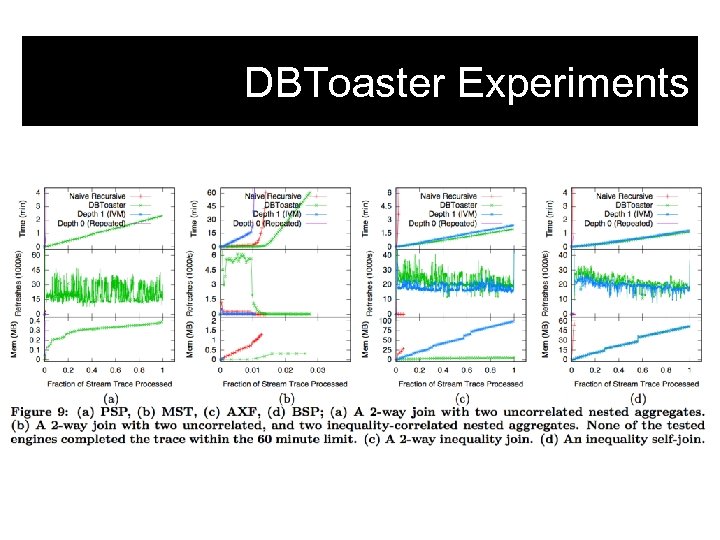
DBToaster Experiments Both classical view maintenance and compilation of main-memory operators 1 -4 orders of magnitude slower.

31 Talk Overview • Classic DBToaster • The new backend: Scala & LMS • Towards a compiler for Web. DAMLog

32 DSL Compiler Construction • We will live in a fast-growing ecosystem of DSLs • • We need tools for quickly creating programming environments. • • Quickly developed and revised Compilers, VMs, … Lightweight Modular Staging (LMS)
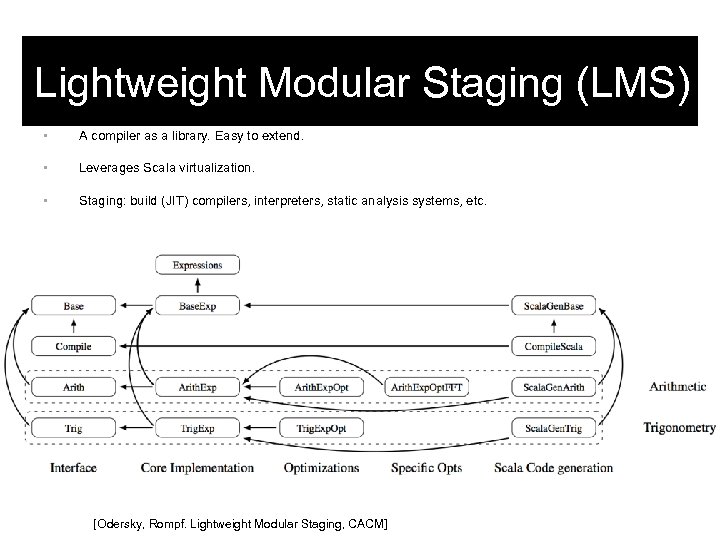
Lightweight Modular Staging (LMS) • A compiler as a library. Easy to extend. • Leverages Scala virtualization. • Staging: build (JIT) compilers, interpreters, static analysis systems, etc. [Odersky, Rompf. Lightweight Modular Staging, CACM]

In the LMS Library • Duplicate expression elimination. • Dead code elimination • Loop fusion • Loop and recursion unrolling. • Code generators. • All this for general Scala (!) • Example: D/FFT: turn recursive def into circuit automatically. Delite (Stanford PPL/EPFL): built on top of LMS • • further code generators (C/CUDA, …) example DSLs (Opti. ML, Opti. Ql, Opti. Graph, Green. Marl, …)

Current work on LMS • Automatic lifting of collection types, functions, classes • Fusion in the presence of side-effects • Global, cost-based optimization • Lightweight embeddings (Yin. Yang) • Joint work of Oracle Labs, Odersky’s Lab (Scala), and us • • Ph. D students V. Jovanovich, A. Shaikhha, and M. Dashti. Staff researchers A. Noetzli, T. Coppey

javac, Graal, and LMS • Oracle is working on replacing the current javac by a completely new compiler. • • Codename: Graal is based on LMS: it will be able to stage compilation in various ways. • • Typically it will JIT to native and won’t need a VM. Adaptivity as in the Hot. Spot VM.
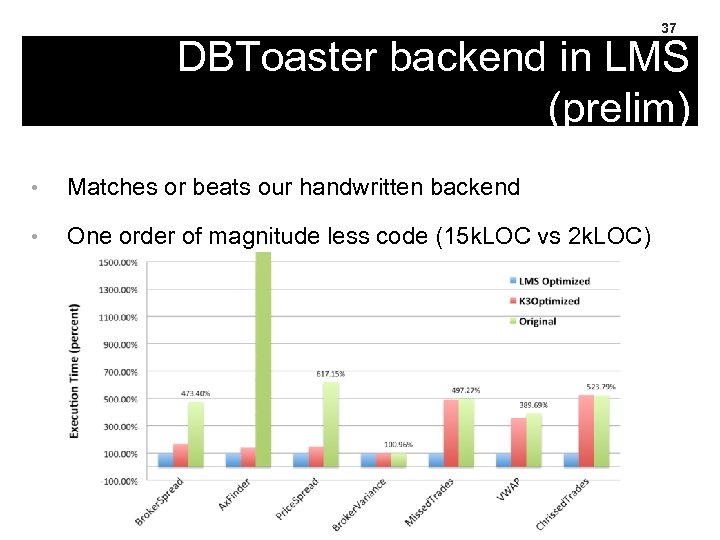
37 DBToaster backend in LMS (prelim) • Matches or beats our handwritten backend • One order of magnitude less code (15 k. LOC vs 2 k. LOC)

38 We observed that Scala is faster than C++, why • Boost/C++: JVM/Oracle Java 7: • Add : 0. 309 • Add : 0. 215 • Clear : 0. 400 • Clear : 0. 001 • Aggr : 0. 090 • Aggr : 0. 021 • Update : 0. 107 • Update : 0. 072 Hashmap costs

39 Talk Overview • Classic DBToaster • The new backend: Scala & LMS • Towards a compiler for Web. DAMLog

40 Domain Maintenance in DBToaster: a Datalog problem • Domaintenance: deciding what to have and keep in the domains of the hashmaps. • Why important: window queries, where the window of relevant values moves: • • e. g. sliding k-day median price of a stock. IVM is about memoization, but sometimes it is important to remove data because it is costly to keep maintaining them. • “View caches”

Domain Maintenance in DBToaster: a Datalog problem What are the domains of these maps? • In general there are binding patterns on the domains. Example: Q[x, y] <- R(x), (S(y), x<y). Map m[x^b, y^f] = S(y), x<y. • • The programs have been recursively decomposed by the DBToaster rewriting algo. Determining the domains of maps is essentially magic sets/QSQ, where we look for the supplementary relations!

42 IVM and datalog • We can rewrite datalog programs using our techniques rule by rule. No new ideas needed. • • Seminaive evaluation is classical IVM on datalog rules. This does everything seminaive eval does, and (much) more. Can we do better? How? If we want to support deletion, we get to bag semantics. • But we don’t know how to deal with bags and recursion.

43 IVM and datalog • Joint work with V. Kuncak: synthesis of incremental programs. • • • Search for programs achieving our goal, rather than syntactically rewriting them. Already works for insertions into various (balanced) tree data structures (from invariants!). Efficient runtime verification (in Java, for instance). • Incrementally maintaining assertions. • This is getting hot in PL.

44 Notions of recursion • Datalog recursion – additional querying power • • E. g. computing graph queries -- Graphlog, Socialite Modeling Dynamics – database in each iteration corresponds to a different time point/state. • • Bloom, Web. DAMLog: capturing distributed computation, nw protocols Triggers that call triggers? cf. Active databases.

45 Challenges • Triggers that call triggers: which notion of consistency, if you want to capture both classical recursion for its expressiveness and distributed dynamic computations? • Aggregates(bag semantics) and fixpoints. • • You need bag semantics and aggregates for interesting analytics. But then we generally don’t have fixpoints (see e. g. Val’s work) and it’s too hard to tell when we are not in trouble.

46 Challenges • We can think of it as a relational programming language and leave all worries about consistency and termination to the programmer. • • It would be important to make guarantees though. Argh I am running out of time making these sli

Thank you!

Use case: Algorithmic trading • High-frequency algorithmic trading is getting huge: • • • Q 1/2009 in the US: 73% of all trades in equities. ~15% annual profit margin across the industry! Algo execution practices: • • • Extremely low latencies: stock exchanges make 3 ms guarantees Algos run in data centers close to exchanges Algo development practices: • • • Algos and underlying models are constantly monitored, improved, and experimented with in large simulations Analytics have to be performed at very high data rates, beyond DBMS or stream engines (expressiveness!). The fastest algo makes money. Currently, algos written on a low level (C). Constant backtesting and improvement means coding bottleneck: Many programmers needed, software crisis.

A ring of relations

50 Parameterized GMRs • A parameterized GMR is a function that takes an environment to a GMR. • Can be used to model binding passing in query calculi. • Conditions etc. do not have finite support/are not finite relations. Valuations of variables can be passed from the left. • Still a ring! • + and * strictly generalize monoid rings (GMRs) and thus union and join, resp.

Modeling binding passing in queries Strictly generalizes monoid rings and thus union& join!
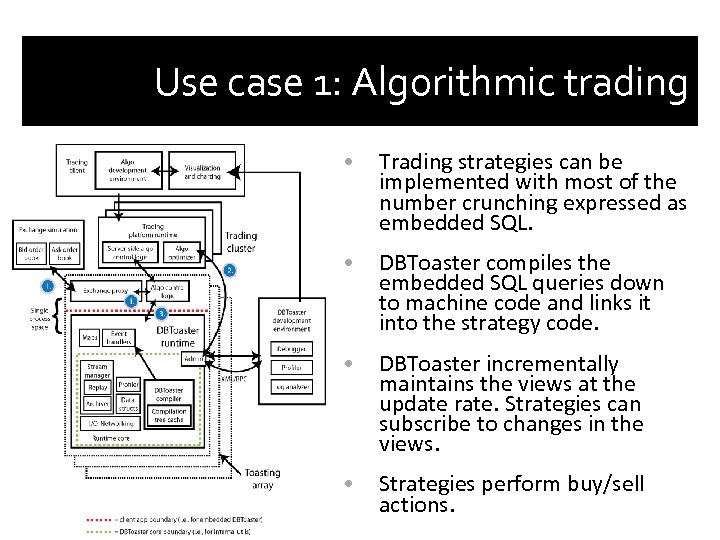
Use case 1: Algorithmic trading • Trading strategies can be implemented with most of the number crunching expressed as embedded SQL. • DBToaster compiles the embedded SQL queries down to machine code and links it into the strategy code. • DBToaster incrementally maintains the views at the update rate. Strategies can subscribe to changes in the views. • Strategies perform buy/sell actions.
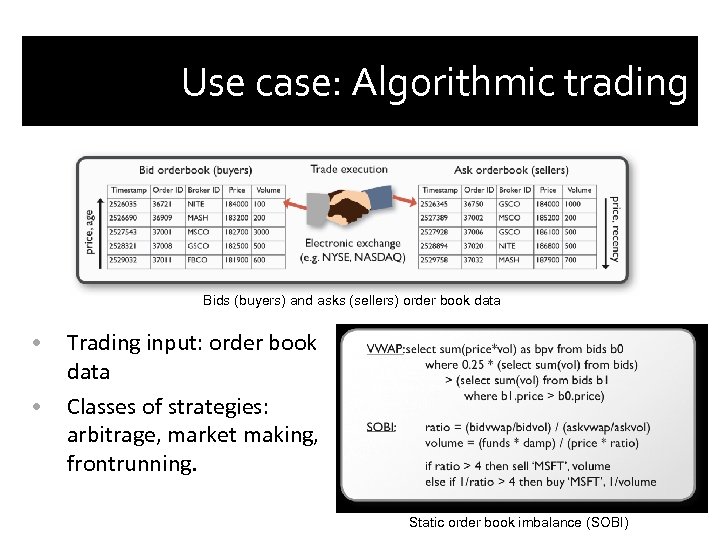
Use case: Algorithmic trading Bids (buyers) and asks (sellers) order book data • • Trading input: order book data Classes of strategies: arbitrage, market making, frontrunning. Static order book imbalance (SOBI)

NC 0 C programs

Parallel complexity consequences • In an NC 0 C statement, there is NO overlap among the variables occurring in distinct atomic rhs terms. • Statements with for-loops are relational products, not joins: no filtering. • Distributed implementation: no communication is needed to determine where changes have to be sent. • Purely push-based implementation sends minimal amount of data. • No need for bloom-joins or synchronization: lightweight eventual consistency approach!
DBToaster Experiments
DBToaster Experiments
DBToaster Experiments

Systems efforts in the DBToaster Project • The DBToaster engine for update streams • Applications: Low-latency algorithmic trading (order books), clickstream analysis, … • Cumulus: • OLAP using a distributed key-value store plus a very simple message passing protocol for view maintenance. • Exact aggregate view maintenance in realtime! • Squall: • A distributed online aggregation system based on Storm.
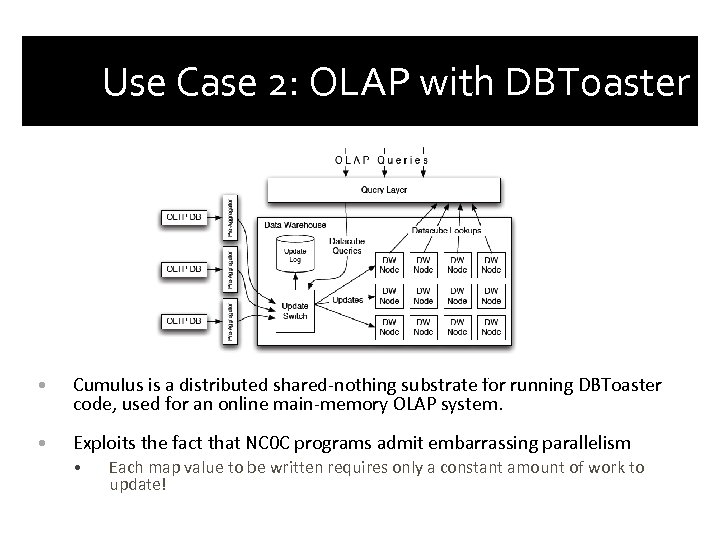
Use Case 2: OLAP with DBToaster • Cumulus is a distributed shared-nothing substrate for running DBToaster code, used for an online main-memory OLAP system. • Exploits the fact that NC 0 C programs admit embarrassing parallelism • Each map value to be written requires only a constant amount of work to update!
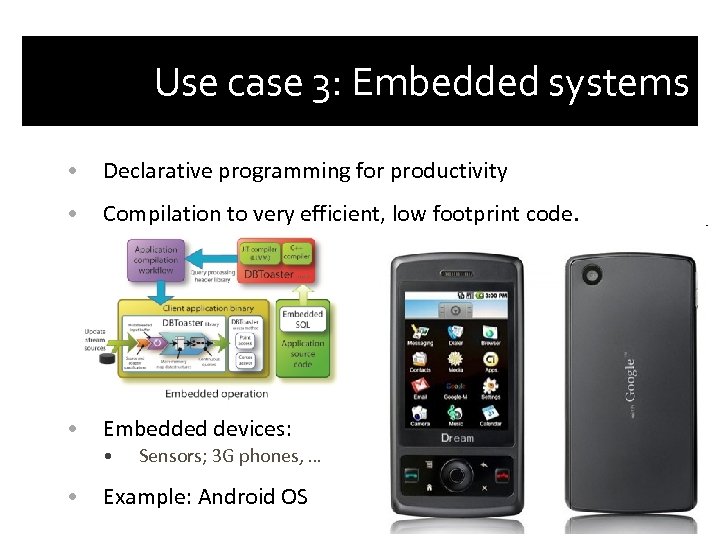
Use case 3: Embedded systems • Declarative programming for productivity • Compilation to very efficient, low footprint code. • Embedded devices: • • Sensors; 3 G phones, … Example: Android OS

Conclusions • Work at the intersection of databases and compilers is hot! • A clean foundation for incremental view maintenance (IVM) based on algebra. • An aggressive IVM technique based on compilation • Can eliminate all joins • Embarassing parallelism (NC 0)! • Systems efforts towards ultra-high frequency view refreshment (tens of k. Hz), real-time analytics and data warehousing. • The system has been released at www. dbtoaster. org

What does Scala buy us (vs Java)? • Functional programming, pattern matching convenient for compiler construction. • Language virtualization • • Mix-in composition • • no need to write parsers if your language is a superset of a subset of Scala. Easy to refine behavior in a clean, fine-grained way. Scala can be used as a scripting language. + All the benefits of Java (libs, linkability, …).

DSL Embeddings • Shallow embedding: DSL programs are programs of the host language that use a library of DSL operators. • Deep embedding (e. g. LMS): create AST, manipulate AST. • • • Pros: Necessary for optimization, custom code generation Cons: Compilation slower, error messages nearly unreadable. Yin-Yang: transplants/rewires shall DSL embeddings at compile time into to deep embeddings. • • Faster program type checking, prototyping, and debugging. Error messages much more readable. V. Jovanovic, N. Pham, V. Nikolaev, V. Ureche, S. Stucki, K, M. Odersky, “Yin-Yang: Transparent Deep Embedding of DSLs”, under submission.

LMS Example

LMS Example

Lifting Collection Libraries in LMS • Develop lift-friendly data structure (hashmaps, trees) libraries. • Extend LMS to be able to lift them whole. • Inline library code completely. Current work on the DBToaster compiler: • Rewrite backend using LMS (currently: OCAML) • Extend LMS to match the performance of our own codebase. • Inline collections using LMS, row-store/column-store pivot. Joint work with Y. Ahmad, M. Dashti, V. Jovanovich, O. Kennedy, A. Noetzli, T. Rompf.
22908177e4745bdcfd32998fff02f3e9.ppt